【数据结构】排序(上)

个人主页~
堆排序看这篇~
还有这篇~
排序
- 一、排序的概念及应用
- 1、概念
- 2、常见的排序算法
- 二、常见排序的实现
- 1、直接插入排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 2、希尔排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 3、选择排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 4、堆排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 5、冒泡排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 6、快速排序
- (1)基本思想
- (2)代码实现
- ①hoare版本
- ②挖坑法版本
- ③前后指针版本
- (3)时间复杂度
- (4)空间复杂度
一、排序的概念及应用
1、概念
排序就是按照某一关键字递增和递减排列起来的操作
排序在生活中非常常用,成绩、排行等等一切跟数字字母等有关的都能够排序
2、常见的排序算法
常见的排序算法有
插入排序:直接插入排序,希尔排序
选择排序:选择排序,堆排序
交换排序:冒泡排序、快速排序
归并排序:归并排序
二、常见排序的实现
1、直接插入排序
(1)基本思想
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列
(2)代码实现
//我们看做一个一个插入
void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){//从0到end都有序,tmp插入排序int end = i - 1;//end存储插入前的最后一个元素的下标,也就是第i-1个数据int tmp = a[i];//tmp是插入的数据,也就是第i个数据while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}//如果前边比后边大,就交换并且--end,继续向前比较else{break;//直到后边比前边大}}a[end + 1] = tmp;//将此时end+1下标的位置赋值tmp,后边的数据全都往后移了一位}
}
封装一个打印数组的函数
void ArrPrint(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}
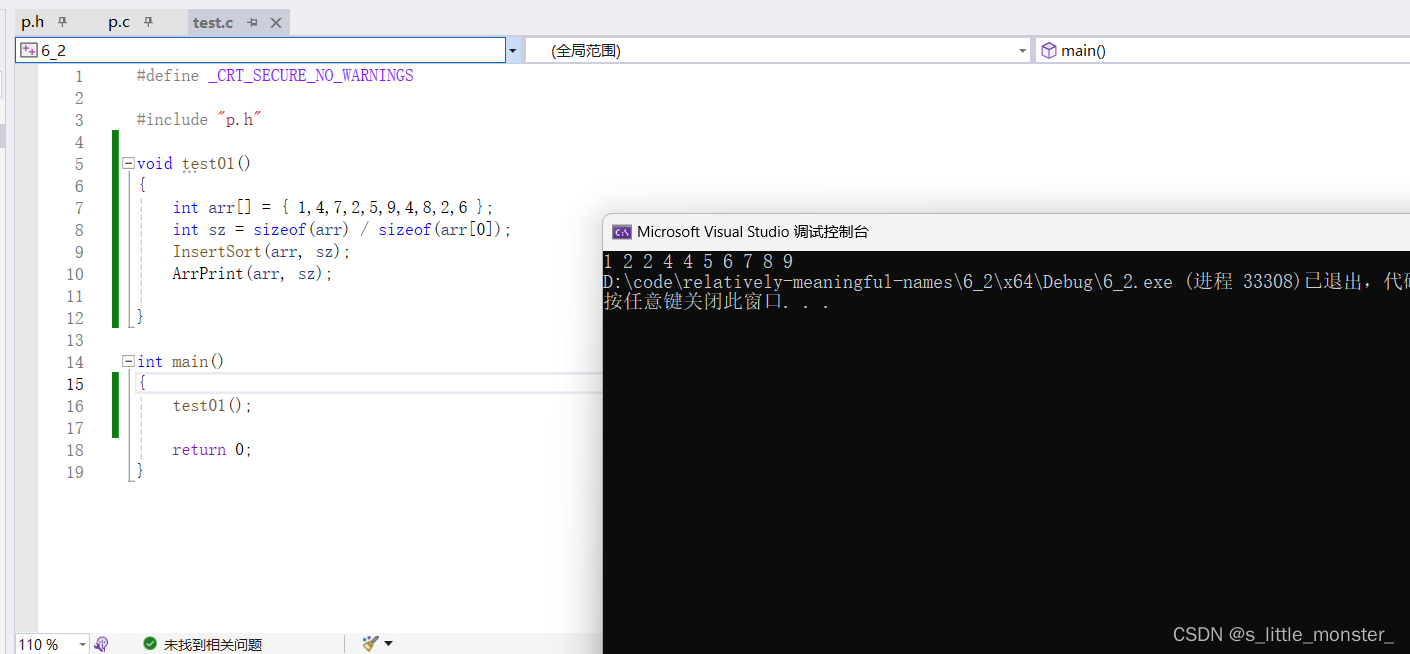
(3)时间复杂度
如果按照最坏的情况:
第一次排不需要比较
第二次需要比较一次
第三次需要比较两次
…
第N次需要比较N-1次
F(N)=0+1+2+3+…+N-1 = (N-1)*(N)/2
所以直接插入排序的最坏时间复杂度为O(N^2)
最好时间复杂度就是有序数组O(N)
所以直接插入排序是介于它们之间的,这才有了希尔排序这种优化算法,降低了时间复杂度
(4)空间复杂度
没有占用额外空间,O(1)
2、希尔排序
(1)基本思想
希尔排序可以说是高级的直接插入排序,它是希尔通过观察和实践在直接插入排序的基础上进行算法优化,将时间复杂度降低
希尔排序分为两步:
第一步:预排序,是将无序的数组排序至接近有序
第二步:直接插入排序
当gap越小越接近有序,gap越大预排序的速度会更快
当gap为1时,就是直接插入排序
简单来说希尔排序就是粗排后细排
(2)代码实现
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//分为三组,最后加一可以保证最后一次的while循环gap等于1,相当于直接插入排序for (int i = 0; i < n - gap; i++){int end = i;
//每组的最后一个数字(这里的最后一个是指一个一个往里面插的最后一个数字,并不是真正的最后一个数字)int tmp = a[end + gap];//记录待插入数字while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}elsebreak;}//同直接插入排序,差别是分了组,每次要对比的数字的下标差了gapa[end + gap] = tmp;}}
}
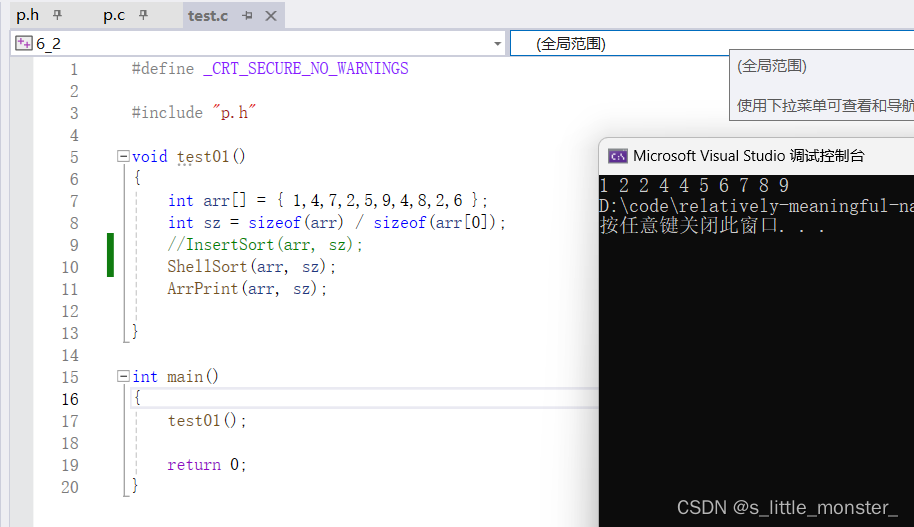
(3)时间复杂度
希尔排序的时间复杂度并不好计算,因为gap的取值很多,我们没办法通过简单的计算来得出结果,这是一个数学上的难以解答的问题,资料中显示,它的时间复杂度在O(n^1.25)到O(1.6*n ^1.25)之间,我们粗略表示成O(n ^1.3)
(4)空间复杂度
没有占用额外空间,O(1)
3、选择排序
(1)基本思想
遍历数组,每一次将最大和最小的数据挑出来放到数列的起始和末尾位置,知道所有元素全部排完
这是一种超级慢的排序方式,实际使用中很少用
(2)代码实现
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;}void SelectSort(int* a, int n)
{int right= n - 1;//定位到数组最后一个元素下标int left = 0;//定位到数组第一个元素下标while (left < right){int min = left;//先将left作为最开始的最小值int max = right;//先将right作为最开始的最大值for (int i = left; i <= right; i++){if (a[i] < a[min])min = i;if (a[i] > a[max])max = i;}//在left和right之间选出最大和最小的数Swap(&a[left], &a[min]);//交换a[left]与a[min]if (left == max)max = min;//这里注意,当最大值与left重叠时,将位置修正再交换Swap(&a[right], &a[max]);left++;right--;}
}
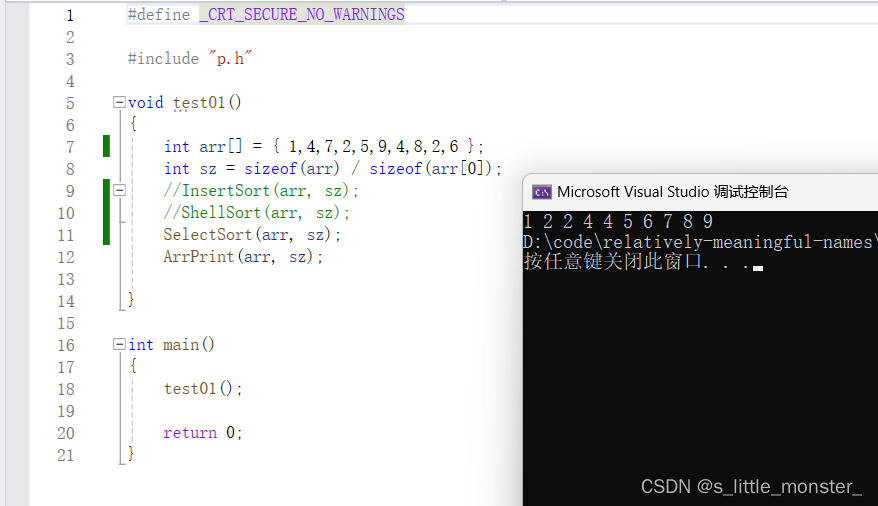
(3)时间复杂度
它的时间复杂度就是等差数列求和,可以很容易的看出来它的时间复杂度为O(N^2)
(4)空间复杂度
没有占用额外空间,O(1)
4、堆排序
在之前的文章中有详细的解释,我们可以来到二叉树-堆文章中来详细了解
(1)基本思想
利用堆的特性,即小堆堆顶最小,大堆堆顶最大的性质,来进行升序或降序排序
(2)代码实现
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void AdjustDown(int* a, int n,int parent)
{int child = parent * 2 + 1;while(child < n){if (child + 1 < n && a[child] < a[child + 1]){child++;}//调出值较大的那个孩子if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}//交换后让孩子当爹,使其跟它的孩子比较elsebreak;}
}void HeapSort(int* a, int n)
{//parent = (child-1) / 2,i的初始值是最后一个元素的父节点for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//调整出一个大堆int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);//交换首尾元素AdjustDown(a, end, 0);end--;}
//每次调整都会将最大的一个数放在当前调整范围的最后一个位置,而调整范围的最后一个位置每次都会向前一个,直到成为升序数组
}
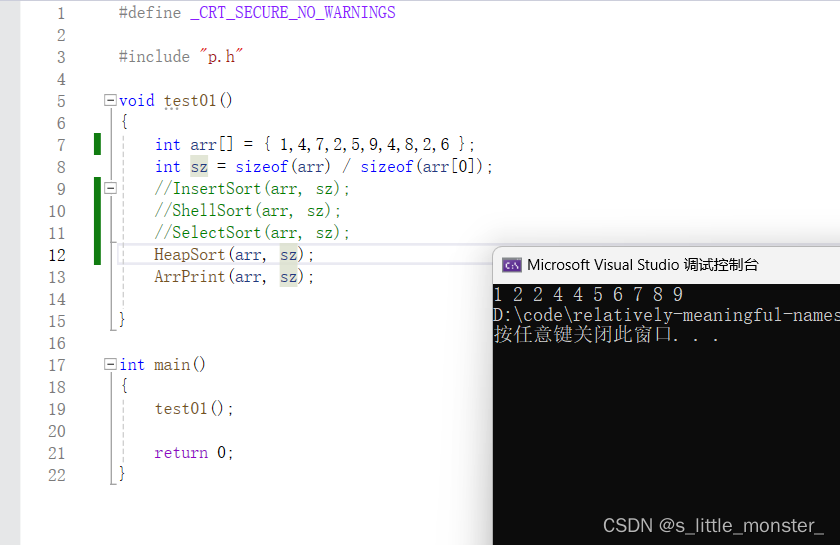
(3)时间复杂度
在前面链接中的文章中我们计算过它的时间复杂度,O(N*log₂N)
(4)空间复杂度
没有额外申请空间,O(1)
5、冒泡排序
(1)基本思想
冒泡排序是我们初识C语言时的接触到的第一个排序方式,也可以说是最鸡肋的排序方式,简单易懂但效率很低,就是两两元素相互比较,大的往后移动,遍历一遍下来最大的就到最后了,以此类推实现排序
这里我就不过多解释了
(2)代码实现
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n - i - 1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}
(3)时间复杂度
相当于等差数组求和,n-1 + n-2 + … + 1
F(N) = (N-1+1)/2 * N/2
时间复杂度为O(N^2)
(4)空间复杂度
没有占用额外空间,空间复杂度为O(1)
6、快速排序
(1)基本思想
任取待排序序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素小于基准值,右子序列中所有元素大于基准值,然后在左右子序列中重复该过程,直到排序完成
这里我们每一次取的基准值都是左数第一个元素
(2)代码实现
①hoare版本
int PartSort1(int* a, int left, int right)
{int keyi = left;//将最左边的元素作为关键元素,即基准值,记录它的下标while (left < right){while (left < right && a[keyi] <= a[right]){right--;}while (left < right && a[keyi] >= a[left]){left++;}Swap(&a[left], &a[right]);
//左右两边向中间逼近,在右边找到小于基准值的数字,在左边找到大于基准值的数字,两者交换}Swap(&a[keyi], &a[left]);//循环出来之后,说明left与right相遇了,也就是说此时的这个位置左边的数字全部比基准值小,右边的数字都比基准值大,将这个位置的数字与基准值位置的数字交换位置return left;//将此时的基准值返回
}void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort1(a, left, right);//将区间分成三个部分:keyi,keyi左,keyi右QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);//对剩下的区间继续排序
}

②挖坑法版本
int PartSort2(int* a, int left, int right)
{int key = a[left];//存下坑里的数字int hole = left;//把最左边的位置作为坑while (left < right){while (left < right && a[right] >= key)right--;//找到a[right] < key的位置跳出循环a[hole] = a[right];hole = right;//把这个位置挖新坑,将坑里的值存起来while (left < right && a[left] <= key)left++;a[hole] = a[left];hole = left;//右边挖完左边挖,左边找大于基准值的}a[hole] = key;//将最开始存下来的基准值填到此时剩下的坑里return hole;
}void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort2(a, left, right);//将区间分成三个部分:keyi,keyi左,keyi右QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);//对剩下的区间继续排序
}

③前后指针版本
int PartSort3(int* a, int left, int right)
{int prev = left;//初始前指针为最左边的元素int cur = left + 1;//初始后指针为前指针的后一个元素int keyi = left;//存下前指针的下标作为基准值下标while (cur <= right){while (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);
//如果后指针指向的数字大小小于基准值,并且前指针的后一个指针不为后指针,那么前后指针指向位置的值交换
//当后指针指向的值小于基准值时,前指针都会往后走(这里的知识涉及到逻辑语句的短路)cur++;//后指针往后走}Swap(&a[prev], &a[keyi]);keyi = prev;//最后前指针所指向元素的大小一定大于基准值,将他们交换,此时的基准值左边除了第一个都比它小,右边都比它大return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort3(a, left, right);//将区间分成三个部分:keyi,keyi左,keyi右QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);//对剩下的区间继续排序
}

(3)时间复杂度
快速排序是一种类二叉树类型的排序,所以它的时间复杂度为O(N*log₂N),计算方法同二叉树
(4)空间复杂度
递归创建类二叉树,空间复杂度为O(log₂N)
下期再见~

相关文章:

【数据结构】排序(上)
个人主页~ 堆排序看这篇~ 还有这篇~ 排序 一、排序的概念及应用1、概念2、常见的排序算法 二、常见排序的实现1、直接插入排序(1)基本思想(2)代码实现(3)时间复杂度(4)空间复杂度 2…...
:)
vue3+el-plus对eleplus对el-table表格进行拖拽(使用sortablejs进行列拖拽和行拖拽):
如有对表格拖拽进行限制某列或某行不进行拖拽的需求,请点击: vue3ele-plussortableJs对el-table使用sortableJs插件对表格拖拽时限定某列或某行不允许拖拽-CSDN博客 如果你已实现拖拽需求,但拖拽后发现表头并未改变的话,请点击&…...

Nginx如何隐藏版本号
1 找到nginx.conf配置文件进行修改 http{...server{listen 80 default_server;listen [::]:80 default_server;server_name _;root /usr/share/nginx/html;server_tokens off; #添加这一项就可以了location / {}error_page 404 /404.html;location /40…...

用C#(WinForm)开发触摸屏,体验感满满
用C#(WinForm)开发触摸屏,体验感满满...
)
LaneKeepingEnv(自动驾驶仿真)
LaneKeepingEnv环境的工作原理可以归纳如下: 初始化阶段: 环境在创建时,会调用__init__方法进行初始化。初始化过程中,会设置一些关键的属性,如lane(当前车道)、lanes(所有车道的列…...

C++类与对象(拷贝与类的内存管理)
感谢大佬的光临各位,希望和大家一起进步,望得到你的三连,互三支持,一起进步 个人主页:LaNzikinh-CSDN博客 文章目录 前言一.对象的动态建立和释放二.多个对象的构造和析构三.深拷贝与浅拷贝四.C类的内存管理总结 前言 …...

C语言----字符函数和字符串函数
在编程的过程中,我们要经常处理字符和字符串,为了方便操作字符和字符串,c语言标准库中提供的一系列库函数,接下来我们就开始学习与认识他们 1.字符分类函数 c语言中有一系列的函数是专门做字符分类的,也就是一个字符…...
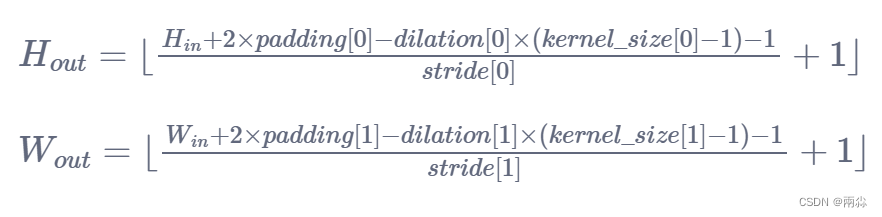
神经网络 torch.nn---Convolution Layers
torch.nn — PyTorch 2.3 documentation torch.nn - PyTorch中文文档 (pytorch-cn.readthedocs.io) torch.nn和torch.nn.functional的区别 torch.nn是对torch.nn.functional的一个封装,让使用torch.nn.functional里面的包的时候更加方便 torch.nn包含了torch.nn.…...
Linux常用基本命令-操作
目录 一、shell 1、什么是shell 二、Linux基本的命令分类 1、内部命令和外部命令 2、查看内部命令 2.1、help命令 2.2、enable 命令 2.3、type命令 2.4、whereis命令 2.5、which 命令 2.6、hash缓存 编辑 三、Linux常用命令 1、Linux命令格式 2、编辑Linux命…...
搭建全文搜索引擎)
从零开始使用 Elasticsearch(8.14.0)搭建全文搜索引擎
Elasticsearch 是目前最常用的全文搜索引擎。它可以快速地存储、搜索和分析海量数据,广泛应用于维基百科、Stack Overflow、Github 等网站。 Elasticsearch 的底层是开源库 Lucene。直接使用 Lucene 需要写大量代码,而 Elasticsearch 对其进行了封装&am…...
流程与IT双驱动:锐捷网络如何构建持续领先的服务竞争力?
AI大模型及相关应用进入“竞赛时代”,算力作为关键要素备受关注,由于算力行业对网络设备和性能有较大需求,其发展也在推动ICT解决方案提供商加速升级,提升服务响应速度和服务质量。 锐捷网络是行业领先的ICT基础设施及行业解决方…...

CopyOnWriteArrayList 详细讲解以及示范
CopyOnWriteArrayList是Java集合框架中的一种线程安全的列表实现,特别适用于读多写少的并发场景。 它是通过“写时复制”(Copy-On-Write)策略来保证线程安全的,这意味着当有线程尝试修改列表时,它会先复制原列表到一个…...
01-Java和Android环境配置
appium是做app自动化测试最火的一个框架,它的主要优势是支持android和ios,同时也支持Java和Python脚本语言。而学习appium最大的难处在于环境的安装配置,本文主要介绍Java和Android环境配置,在后续文章中将会介绍appium的安装和具…...
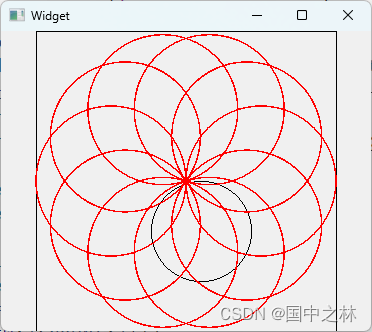
【qt】视口和窗口坐标
视口和窗口坐标 一.视口和窗口坐标的原理二.视口和窗口坐标的好处三.演示好处四.总结 一.视口和窗口坐标的原理 在绘图事件中进行绘图 void Widget::paintEvent(QPaintEvent *event) {QPainter painter(this);QRect rect(200,0,200,200);painter.drawRect(rect);//设置视口的…...

优化SQL查询的策略和技巧 - AI提供
优化SQL查询以提高处理大型数据集的数据库性能是一个重要课题。 以下是一些关键策略和技巧,可以帮助您提升查询效率: 1、创建合适索引: 针对频繁出现在WHERE、JOIN、ORDER BY和GROUP BY子句中的列创建索引。索引能够显著加速数据检索过程。…...

平安科技智能运维案例
平安科技智能运维案例 在信息技术迅速发展的背景下,平安科技面临着运维规模庞大、内容复杂和交付要求高等挑战。通过探索智能运维,平安科技建立了集中配置管理、完善的运营管理体系和全生命周期运维平台,实施了全链路监控,显著提…...

基于深度学习的向量图预测
基于深度学习的向量图预测 向量图预测(Vector Graphics Prediction)是计算机视觉和图形学中的一个新兴任务,旨在从像素图像(栅格图像)生成相应的向量图像。向量图像由几何图形(如线条、曲线、多边形等&…...
与$rawfile(““)的区别)
鸿蒙HarmonyOS $r(““)与$rawfile(““)的区别
在鸿蒙(HarmonyOS)开发中,$r(“”) 和 $rawfile(“”) 是两种不同的资源引用方式,它们分别用于引用不同的资源类型。 1、$r(“”) $r 函数通常用于引用字符串、颜色、尺寸、样式等定义在资源文件(如 strings.json, c…...

简单了解java中的Collection集合
集合 1、Collection-了解 1.1、集合概述 集合就是一种能够存储多个数据的容器,常见的容器有集合和数组 那么集合和数组有什么区别嘞? 1、集合长度可变,数组的长度不可变 2、集合只能存储引用数据类型(如果要存储基本数据类型…...
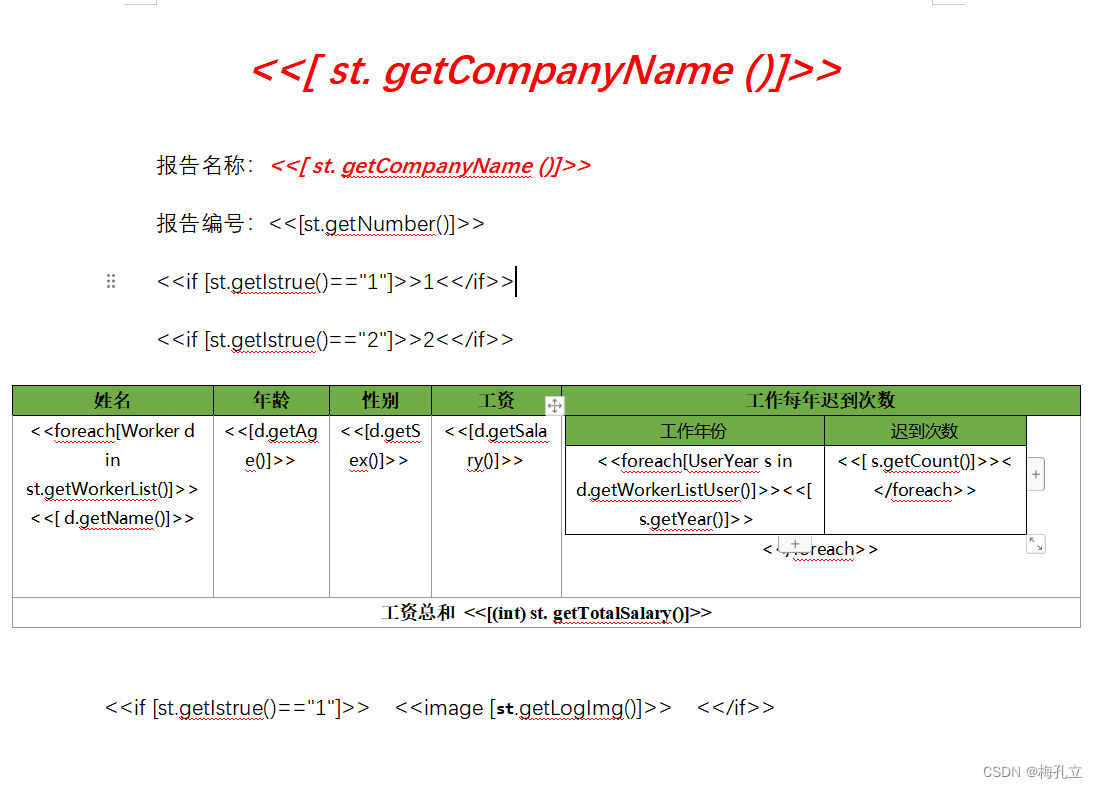
java 实现导出word 自定义word 使用aspose教程包含图片 for 循环 自定义参数等功能
java 实现导出word 主要有一下几个知识点 1,aspose导入 jar包 和 java编写基础代码下载使用 aspose-words jar包导入 aspose jar 包 使用 maven导入java代码编写 2,if判断 是否显示2,显示指定值3,循环显示List 集合列表 使用 fore…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
