数据结构笔记-2、线性表
2.1、线性表的定义和基本操作
如有侵权请联系删除。
2.1.1、线性表的定义:
线性表是具有相同数据类型的 n (n>=0) 个数据元素的有限序列,其中 n 为表长,当 n = 0 时线性表是一个空表。若用 L 命名线性表,则其一般表示为:
L = ( a 1 , a 2 , a 3 , . . . , a i , x i + 1 , . . . , a n ) L=(a_1,a_2,a_3,...,a_i,x_{i+1},...,a_n) L=(a1,a2,a3,...,ai,xi+1,...,an)
式中, a 1 a_1 a1 是唯一的“第一个元素”,又称表头元素; a n a_n an 是唯一的“最后一个元素”,又称表尾元素。除第一个元素外,每个元素有且仅有一个直接前驱。除最后一个元素外,每个元素有且仅有一个直接后驱。
由此,线性表的特点是:
- 表中元素的个数有限。
- 表中元素具有逻辑上的顺序性,表中数据有其先后次序。
- 表中元素都是数据元素,每个元素都是单个数据。
- 表中元素的数据类型都相同,这意味着每个元素都占有相同大小的存储空间。
- 表中元素具有抽象性,即仅讨论元素间的逻辑关系,而不考虑元素究竟表示什么内容。
2.1.2、线性表的操作:
线性表的主要操作如下:
InitList(&L) :初始化表。构造一个空的线性表。
Length(L) :求表长。返回线性表 L 的长度,即 L 中数据元素的个数。
LocateElem(L,e) :按值查找操作。在表 L 中查找具有给定关键字值的元素。
GetElem(L,i) :按位查找操作。获取表 L 中第 i 个位置的元素的值。
ListInsert(&L,i,e) :插入操作。在表 L 中的第 i 个位置上插入指定元素 e 。
ListDelete(&L,i,&e) :删除操作。删除表 L 中第 i 个位置的元素,并用 e 返回删除元素的值。
PrintList(L) :输出操作。按前后顺序输出线性表 L 的所有元素值。
Empty(L) :判空操作。若 L 为空表,则返回 true,否则返回 false。
DestroyList(&L) :销毁操作。销毁线性表,并释放线性表 L 所占用的内存。
2.2、线性表的顺序表示:
2.2.1、顺序表的定义:
线性表的顺序储存又称顺序表。它是用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理位置上也相邻。第 1 个元素存储在线性表的起始位置,第 i 个元素的存储位置后面紧跟着存储位置的是第 i + 1 个元素,称 i 为元素 a i a_i ai 在线性表中的位序。因此,顺序表的特点是表中元素的逻辑顺序与物理顺序相同。
假设线性表 L 存储的起始地址为 LOC(A),sizeof(ElemType) 是每个数据元素所占用内存空间的大小,则表 L 所对应的顺序存储如下图所示。

通常用高级语言中的数组来描述线性表的顺序存储结构。
假定线性表的元素类型为 ElemType ,则线性表的顺序存储类型描述为:
#define MaxSize 50 //定义线性表的最大长度
typedef struct {ElemType data[MaxSize]; //顺序表的元素int length; //顺序表的当前长度
} SqList; //顺序表的类型定义
一维数组可以是静态分配的,也可以是动态分配的。在静态分配时,由于数组的大小和空间事先已经固定,一旦空间占满,再加入新的数据就会产生溢出,进而导致程序崩溃。
而在动态分配时,存储数组的空间实在程序执行过程中通过动态存储分配语句分配到,一旦数据空间占满,就另外开辟一块更大的存储空间,用以替换原来的存储空间,从而达到扩充存储数组空间的目的,而不需要为线性表依次性地划分所有空间。
#define InitSize 100 //表长度的初始定义
typedef struct {ElemType *data; //指示动态分配数组的指针int MaxSize,length; //数组的最大容量和当前个数
} SeqList; //动态分配数组顺序表定义
C语言初始动态分配语句为:
L.data = (ElemType*)malloc(sizeof(ElemType)*InitSize);
顺序表最主要的特点是随机访问,即通过首地址和元素序号可在时间 O(1) 内找到指定的元素。
顺序表的存储密度高,每个结点只存储数据元素。
顺序表逻辑上相邻的元素物理上也相邻,所以插入和删除操作需要移动大量元素。
2.2.2、顺序表上基本操作的实现:
(1)、插入操作:
在顺序表 L 的第 i (1<= i <= L.Length+1) 个位置插入新元素 e 。若 i 的输入不合法,则返回 false ,表示插入失败;否则,将第 i 个元素及其后的所有元素依次往后移动一个位置,腾出一个空位置插入新元素 e ,顺序表长度增加 1,插入成功,返回 true。
#include "stdio.h"
#define MaxSize 50typedef struct {int data[MaxSize];int length;
} SqList;int ListInsert(SqList *L,int i , int e);int main(){SqList L;L.length = 0;for (int i = 0; i < 9; i++){L.data[i] = i + 1;L.length += 1;}ListInsert(&L,4,10);for (int i = 0; i < L.length; i++){printf("%d,",L.data[i]);}printf("\n%d",L.length);return 0;
}//实现插入算法的主体函数
int ListInsert(SqList *L,int i , int e){if (i < 1 || i > L->length + 1)return 0;if (L->length >= MaxSize)return 0;for (int j = L->length;j >= i;j--)L->data[j] = L->data[j-1];L->data[i - 1] = e;L->length ++;return 1;
}
注意:区别顺序表的为序和数组下标。
最好情况:在表尾插入(i = n + 1),元素后移语句将不执行,时间复杂度为 O(1)。
最坏情况:在表头插入(i = 1),元素后移语句将执行 n 次,时间复杂度为 O(n)。
平均情况:假设 p i p_i pi( p i = 1 / ( n − 1 ) p_i=1/(n-1) pi=1/(n−1))是在第 i 个位置上插入一个结点的概率,则在长度为 n 的线性表中插入一个结点时,所需移动的结点平均次数为:
∑ i = 1 n + 1 p i ( n − i + 1 ) = ∑ i = 1 n + 1 1 n + 1 ( n − i + 1 ) = 1 n + 1 ∑ i = 1 n + 1 ( n − i + 1 ) = 1 n + 1 n ( n + 1 ) 2 = n 2 \sum_{i=1}^{n+1}p_i(n-i+1)=\sum_{i=1}^{n+1}\frac{1}{n+1}(n-i+1)=\frac{1}{n+1}\sum_{i=1}^{n+1}(n-i+1)=\frac{1}{n+1}\frac{n(n+1)}{2}=\frac{n}{2} i=1∑n+1pi(n−i+1)=i=1∑n+1n+11(n−i+1)=n+11i=1∑n+1(n−i+1)=n+112n(n+1)=2n
因此,顺序表插入算法的平均时间复杂度为 O(n)
(2)、删除操作:
删除顺序表 L 中第 i (1 <= i <= L.length)个位置的元素,用引用变量 e 返回。若 i 的输入不合法,则返回 false ;否则,将被删元素赋给引用变量 e ,并将 i + 1 个元素及其后的所有元素依次往前移动一个位置,返回 true。
#include "stdio.h"
#define MaxSize 50typedef struct {int data[MaxSize];int length;
} SqList;int ListInsert(SqList *L,int i , int e);
int ListDelete(SqList *L,int i , int *e);int main(){SqList L;int e;L.length = 0;for (int i = 0; i < 9; i++){L.data[i] = i + 1;L.length += 1;}ListInsert(&L,4,10);ListDelete(&L,4,&e);for (int i = 0; i < L.length; i++){printf("%d,",L.data[i]);}printf("\n%d",e);return 0;
}int ListInsert(SqList *L,int i , int e){if (i < 1 || i > L->length + 1)return 0;if (L->length >= MaxSize)return 0;for (int j = L->length;j >= i;j--)L->data[j] = L->data[j-1];L->data[i - 1] = e;L->length ++;return 1;
}//实现删除算法的主体函数
int ListDelete(SqList *L,int i , int *e){if (i < 1 || i > L->length)return 0;*e = L->data[i-1];for (int j = i;j<L->length;j++)L->data[j-1] = L->data[j];L->length--;return 1;
}
最好情况:删除表尾元素(即 i = n),无须移动元素,时间复杂度为 O(1)。
最坏情况:删除表头元素(即 i = 1),需移动除表头元素以外的所有元素,时间复杂度为 O(n)。
平均情况:假设 p i p_i pi( p i = 1 / n p_i=1/n pi=1/n)是删除第 i 个位置上结点的概率,则在长度为 n 的线性表中删除一个结点时,所需移动结点的平均次数为:
∑ i = 1 n + 1 p i ( n − i ) = ∑ i = 1 n + 1 1 n + 1 ( n − i ) = 1 n ∑ i = 1 n + 1 ( n − i ) = 1 n n ( n − 1 ) 2 = n − 1 2 \sum_{i=1}^{n+1}p_i(n-i)=\sum_{i=1}^{n+1}\frac{1}{n+1}(n-i)=\frac{1}{n}\sum_{i=1}^{n+1}(n-i)=\frac{1}{n}\frac{n(n-1)}{2}=\frac{n-1}{2} i=1∑n+1pi(n−i)=i=1∑n+1n+11(n−i)=n1i=1∑n+1(n−i)=n12n(n−1)=2n−1
因此,顺序表删除算法的平均时间复杂度为 O(n)。
可见,顺序表中插入和删除操作的时间主要耗费在移动元素上,而移动元素的个数取决于插入和删除元素的位置。如下图所示:

(3)、按值查找(顺序查找)
在顺序表 L 中查找第一个元素值等于 e 的元素,并返回其位序。
#include "stdio.h"
#define MaxSize 50typedef struct {int data[MaxSize];int length;
} SqList;int ListInsert(SqList *L,int i , int e);
int ListDelete(SqList *L,int i , int *e);
int LocateElem(SqList *L,int e);int main(){SqList L;int e,index;L.length = 0;for (int i = 0; i < 9; i++){L.data[i] = i + 1;L.length += 1;}ListInsert(&L,4,10);ListDelete(&L,4,&e);for (int i = 0; i < L.length; i++){printf("%d,",L.data[i]);}printf("\n%d",e);index = LocateElem(&L,4);printf("\n%d",index);return 0;
}int ListInsert(SqList *L,int i , int e){if (i < 1 || i > L->length + 1)return 0;if (L->length >= MaxSize)return 0;for (int j = L->length;j >= i;j--)L->data[j] = L->data[j-1];L->data[i - 1] = e;L->length ++;return 1;
}int ListDelete(SqList *L,int i , int *e){if (i < 1 || i > L->length)return 0;*e = L->data[i-1];for (int j = i;j<L->length;j++)L->data[j-1] = L->data[j];L->length--;return 1;
}//实现按值查找算法的主体函数
int LocateElem(SqList *L,int e){int i;for (i = 0;i < L->length;i++)if (L->data[i] == e)return i + 1;return 0;
}
最好情况:查找到元素在表头,仅需比较一次,时间复杂度为 O(1)。
最坏情况:查找到元素在表尾(或不存在),需要比较 n 次,时间复杂度为 O(n)。
平均情况:假设 p i p_i pi( p i = 1 / n p_i=1/n pi=1/n)是查找到元素在第 i (1 <= i <L.length)个位置上的概率,则长度为 n 的线性表中查找值为 e 的元素所需比较多平均次数为 :
∑ i = 1 n p i × i = ∑ n = 1 n 1 n × i = 1 n n ( n + 1 ) 2 = n + 1 2 \sum_{i=1}^{n}p_i\times i=\sum_{n=1}^{n}\frac{1}{n}\times i=\frac{1}{n}\frac{n(n+1)}{2}=\frac{n+1}{2} i=1∑npi×i=n=1∑nn1×i=n12n(n+1)=2n+1
因此,顺序表按值查找算法的平均时间复杂度为 O(n)。
2.3、线性表的链式表示:
链式存储线性表时,不需要使用地址连续的存储单元,即不要求逻辑上相邻的元素在物理位置上也相邻,它通过 “链”建立起元素之间的逻辑关系,因此插入和删除操作不需要移动元素,而只需修改指针,但也会失去顺序表可随机存取的优点。
2.3.1、单链表的定义:
线性表的链式存储又称单链表,它是指通过一组任意的存储单位来存储线性表中的数据元素。为了建立数据元素之间的线性关系,对每个链表结点,除存放元素自身的信息外,还需存放一个指向其后继的指针。单链表结点一般存放两个域,一个时 data 数据域,用于存放数据;另一个 next 为指针域,用于存放后继结点的地址。
单链表中结点类型的描述如下:
typedef struct LNode {ElemType data;struct LNode *next;
}LNode,*LinkList;
利用单链表可以解决顺序表需要大量连续存储单元的缺点,但单链表附加指针域,也存在浪费存储空间的缺点。由于单链表的元素离散地分布在存储空间中,所以单链表是非随机存取的存储结构,即不能直接找到表中某个特定的结点。查找某个特定的接待你时,需要从头开始遍历,依次查找。
通常用头指针来表示一个单链表,如单链表 L ,头指针为 NULL 时表示一个空表。此外,为了操作上的方便,在单链表第一个结点之前附加一个结点,成为头结点。头结点的数据域可以不设任何信息,也可以记录表长等信息。头结点的指针域指向线性表的第一个元素结点,如下图:

头结点和头指针的区分:不管带不带头结点,头指针都始终指向链表的第一个结点,而头结点时带头节点的链表中的第一个结点,结点内通常不存储信息。
引入头结点后,可以带来两个优点。
- 由于第一个数据结点的位置被存放在头结点的指针域中,因此在链表的第一个位置上的操作和在表的其他位置上的操作一致,无需进行特殊处理。
- 无论链表是否为空,其头指针都是指向头结点的非空指针(空表中头结点的指针域为空),因此空表和非空表的处理也就得到了统一。
2.3.2、单链表上基本操作和实现:
1、采用头插法建立单链表:
该方法从一个空表开始,生成新节点,并将读取到的数据存放到信结点的数据域中,然后将新结点插入到当前链表的表头,即头结点之后,如下图:

头插法建立单链表的算法如下:
#include "stdio.h"
#include "stdlib.h"
typedef struct Node {int data;struct Node *next;
}LNode,*LinkList;LinkList List_HeadInsert(LinkList L);int main(){LinkList L,p;L = List_HeadInsert(L);p = L->next;while(p){printf("%d,",p->data);p = p->next;}return 0;
}//实现头插法建立链表的函数,输出结果是输入的逆序,输入1 2 3,输出结果是3,2,1
LinkList List_HeadInsert(LinkList L){LNode *s;int x;L = (LinkList)malloc(sizeof(LNode));L->next = NULL;scanf("%d",&x);while (x!=9999) {s = (LinkList)malloc(sizeof(LNode));s->data = x;s->next = L->next;L->next = s;scanf("%d",&x);}return L;
}
采用头插法建立单链表时,读入数据的顺序与生成的链表的元素的顺序时相反的。每个结点插入的时间为 O(1),设单链表长为 n ,则总时间复杂度为 O(n)。
2、采用尾插法建立单链表:
头插法建立单链表的算法虽然简单,但生成的链表中节点的次序和输入数据的顺序不一致。若希望两者次序一致,则可采用尾插法。该方法将新结点插入到当前链表的表尾,为此必须增加一个尾指针 r ,使其始终指向当前链表的尾结点,如下图:

#include "stdio.h"
#include "stdlib.h"
typedef struct Node {int data;struct Node *next;
}LNode,*LinkList;LinkList List_HeadInsert(LinkList L);
LinkList List_TailInsert(LinkList L);int main(){LinkList L,p;//头插法建立链表的函数调用
// L = List_HeadInsert(L);//尾插法建立链表的函数调用L = List_TailInsert(L);p = L->next;while(p){printf("%d,",p->data);p = p->next;}return 0;
}LinkList List_HeadInsert(LinkList L){LNode *s;int x;L = (LinkList)malloc(sizeof(LNode));L->next = NULL;scanf("%d",&x);while (x!=9999) {s = (LinkList)malloc(sizeof(LNode));s->data = x;s->next = L->next;L->next = s;scanf("%d",&x);}return L;
}//实现尾插法建立链表的函数
LinkList List_TailInsert(LinkList L){int x;L = (LinkList)malloc(sizeof(LNode));LinkList s,r = L;scanf("%d",&x);while (x != 9999){s = (LinkList) malloc(sizeof(LNode));s->data = x;r->next = s;r = s;scanf("%d",&x);}r->next = NULL;return L;
}
3、按序号查找结点:
在单链表中从第一个结点出发,顺时针 next 域逐个往下搜索,直到找到第 i 个结点为止,否则返回最后一个结点指针域 NULL。
按序号查找结点值的算法如下:
#include "stdio.h"
#include "stdlib.h"
typedef struct Node {int data;struct Node *next;
}LNode,*LinkList;LinkList List_HeadInsert(LinkList L);
LinkList List_TailInsert(LinkList L);
LinkList GetElem(LinkList L,int i);int main(){LinkList L,p;//头插法建立链表的函数调用
// L = List_HeadInsert(L);//尾插法建立链表的函数调用L = List_TailInsert(L);p = L->next;while(p){printf("%d,",p->data);p = p->next;}LinkList target = GetElem(L,4);printf("\n%d",target->data);return 0;
}LinkList List_HeadInsert(LinkList L){LNode *s;int x;L = (LinkList)malloc(sizeof(LNode));L->next = NULL;scanf("%d",&x);while (x!=9999) {s = (LinkList)malloc(sizeof(LNode));s->data = x;s->next = L->next;L->next = s;scanf("%d",&x);}return L;
}LinkList List_TailInsert(LinkList L){int x;L = (LinkList)malloc(sizeof(LNode));LinkList s,r = L;scanf("%d",&x);while (x != 9999){s = (LinkList) malloc(sizeof(LNode));s->data = x;r->next = s;r = s;scanf("%d",&x);}r->next = NULL;return L;
}//实现按序号查找结点算法的函数
LinkList GetElem(LinkList L,int i){if (i < 1)return NULL;int j = 1;LinkList p = L->next;while(p != NULL && j < i){p = p->next;j ++;}return p;
}
按序号查找操作的时间复杂度为 O(n)。
4、按值查找表结点:
从单链表的第一个结点开始,由前往后依次比较表中各结点数据域的值,若某结点数据域的值等于给定值 e ,则返回该结点的指针;若整个单链表中没有这样的结点,则返回 NULL。
按值查找表结点的算法如下:
#include "stdio.h"
#include "stdlib.h"
typedef struct Node {int data;struct Node *next;
}LNode,*LinkList;LinkList List_HeadInsert(LinkList L);
LinkList List_TailInsert(LinkList L);
LinkList GetElem(LinkList L,int i);
LinkList LocateElem(LinkList L,int e);int main(){LinkList L,p;//头插法建立链表的函数调用
// L = List_HeadInsert(L);//尾插法建立链表的函数调用L = List_TailInsert(L);p = L->next;while(p){printf("%d,",p->data);p = p->next;}LinkList target = GetElem(L,4);printf("\n%d",target->data);target = LocateElem(L,5);printf("\n%d",target->data);return 0;
}LinkList List_HeadInsert(LinkList L){LNode *s;int x;L = (LinkList)malloc(sizeof(LNode));L->next = NULL;scanf("%d",&x);while (x!=9999) {s = (LinkList)malloc(sizeof(LNode));s->data = x;s->next = L->next;L->next = s;scanf("%d",&x);}return L;
}LinkList List_TailInsert(LinkList L){int x;L = (LinkList)malloc(sizeof(LNode));LinkList s,r = L;scanf("%d",&x);while (x != 9999){s = (LinkList) malloc(sizeof(LNode));s->data = x;r->next = s;r = s;scanf("%d",&x);}r->next = NULL;return L;
}LinkList GetElem(LinkList L,int i){if (i < 1)return NULL;int j = 1;LinkList p = L->next;while(p != NULL && j < i){p = p->next;j ++;}return p;
}//实现按值查找结点的函数如下
LinkList LocateElem(LinkList L,int e){LinkList p = L->next;while (p!=NULL && p->data != e)p = p->next;return p;
}
5、插入结点操作
通过查找到指定结点的前驱结点进行后插操作
插入结点操作将值为 x 的新结点插入到单链表的第 i 个位置上。先检查插入位置的合法性,然后找到待插入位置的前驱结点,即第 i - 1个结点,,再在其后插入新结点。
算法先调用按序号查找算法 GetElem(L,i-1),查找第 i - 1 个结点。假设返回的第 i - 1 个结点为 *p,然后令新结点 *s 的指针域指向 *p 的后继结点,再领结点 *p 的指针域指向新插入的结点 *s。如下图所示:

实现插入结点的代码如下:
#include "stdio.h"
#include "stdlib.h"
typedef struct Node {int data;struct Node *next;
}LNode,*LinkList;LinkList List_HeadInsert(LinkList L);
LinkList List_TailInsert(LinkList L);
LinkList GetElem(LinkList L,int i);
LinkList LocateElem(LinkList L,int e);
LinkList PreInsert(LinkList L,int i,int e);int main(){LinkList L,p;//头插法建立链表的函数调用
// L = List_HeadInsert(L);//尾插法建立链表的函数调用L = List_TailInsert(L);L = PreInsert(L,5,99);p = L->next;while(p){printf("%d,",p->data);p = p->next;}LinkList target = GetElem(L,4);printf("\n%d",target->data);target = LocateElem(L,5);printf("\n%d",target->data);return 0;
}LinkList List_HeadInsert(LinkList L){LNode *s;int x;L = (LinkList)malloc(sizeof(LNode));L->next = NULL;scanf("%d",&x);while (x!=9999) {s = (LinkList)malloc(sizeof(LNode));s->data = x;s->next = L->next;L->next = s;scanf("%d",&x);}return L;
}LinkList List_TailInsert(LinkList L){int x;L = (LinkList)malloc(sizeof(LNode));LinkList s,r = L;scanf("%d",&x);while (x != 9999){s = (LinkList) malloc(sizeof(LNode));s->data = x;r->next = s;r = s;scanf("%d",&x);}r->next = NULL;return L;
}LinkList GetElem(LinkList L,int i){if (i < 1)return NULL;int j = 1;LinkList p = L->next;while(p != NULL && j < i){p = p->next;j ++;}return p;
}LinkList LocateElem(LinkList L,int e){LinkList p = L->next;while (p!=NULL && p->data != e)p = p->next;return p;
}//实现通过第 i 个数据的前驱结点进行插入的函数算法
LinkList PreInsert(LinkList L,int i,int e){ //实现在第i个结点之后进行插入LinkList p,s;s = (LinkList) malloc(sizeof(LNode));p = GetElem(L,i-1); //获取第i个结点的前驱结点s->data = e;s->next = p->next;p->next = s;return L;
}
扩展:对指定结点进行前插操作
假设,我们想将结点 s 插入到 p 之前。那么则需要将 s 插到 p 的后面,然后交换 p->data 与 s->data 域,这样既可以满足了逻辑关系,又能使得时间复杂度为 O(1)。
代码实现如下:
#include "stdio.h"
#include "stdlib.h"
typedef struct Node {int data;struct Node *next;
}LNode,*LinkList;LinkList List_HeadInsert(LinkList L);
LinkList List_TailInsert(LinkList L);
LinkList GetElem(LinkList L,int i);
LinkList LocateElem(LinkList L,int e);
LinkList PreInsert(LinkList L,int i,int e);
LinkList backInsert(LinkList L,int i,int e);int main(){LinkList L,p;//头插法建立链表的函数调用
// L = List_HeadInsert(L);//尾插法建立链表的函数调用L = List_TailInsert(L);L = backInsert(L,5,99);p = L->next;while(p){printf("%d,",p->data);p = p->next;}LinkList target = GetElem(L,4);printf("\n%d",target->data);target = LocateElem(L,5);printf("\n%d",target->data);return 0;
}LinkList List_HeadInsert(LinkList L){LNode *s;int x;L = (LinkList)malloc(sizeof(LNode));L->next = NULL;scanf("%d",&x);while (x!=9999) {s = (LinkList)malloc(sizeof(LNode));s->data = x;s->next = L->next;L->next = s;scanf("%d",&x);}return L;
}LinkList List_TailInsert(LinkList L){int x;L = (LinkList)malloc(sizeof(LNode));LinkList s,r = L;scanf("%d",&x);while (x != 9999){s = (LinkList) malloc(sizeof(LNode));s->data = x;r->next = s;r = s;scanf("%d",&x);}r->next = NULL;return L;
}LinkList GetElem(LinkList L,int i){if (i < 1)return NULL;int j = 1;LinkList p = L->next;while(p != NULL && j < i){p = p->next;j ++;}return p;
}LinkList LocateElem(LinkList L,int e){LinkList p = L->next;while (p!=NULL && p->data != e)p = p->next;return p;
}LinkList PreInsert(LinkList L,int i,int e){ //实现在第i个结点之后进行插入LinkList p,s;s = (LinkList) malloc(sizeof(LNode));p = GetElem(L,i-1); //获取第i个结点的前驱结点s->data = e;s->next = p->next;p->next = s;return L;
}//实现后插结点的函数主题如下
LinkList backInsert(LinkList L,int i,int e){LinkList p,s;int temp;s = (LinkList) malloc(sizeof(LNode));p = GetElem(L,i); //获取第i个结点的前驱结点s->data = e;s->next = p->next;p->next = s;temp = p->data;p->data = s->data;s->data = temp;return L;
}
6、删除结点操作:
删除结点操作是将单链表的第 i 个结点删除。先检查删除位置的合法性,后查找表中第 i - 1 个结点,即被删结点的前驱结点,再将其删除。如下图:

代码实现如下:
#include "stdio.h"
#include "stdlib.h"
typedef struct Node {int data;struct Node *next;
}LNode,*LinkList;LinkList List_HeadInsert(LinkList L);
LinkList List_TailInsert(LinkList L);
LinkList GetElem(LinkList L,int i);
LinkList LocateElem(LinkList L,int e);
LinkList PreInsert(LinkList L,int i,int e);
LinkList backInsert(LinkList L,int i,int e);
LinkList DeleteNode(LinkList L,int i);int main(){LinkList L,p;L = List_TailInsert(L);p = L->next;L = DeleteNode(L,4);while(p){printf("%d,",p->data);p = p->next;}return 0;
}LinkList List_HeadInsert(LinkList L){LNode *s;int x;L = (LinkList)malloc(sizeof(LNode));L->next = NULL;scanf("%d",&x);while (x!=9999) {s = (LinkList)malloc(sizeof(LNode));s->data = x;s->next = L->next;L->next = s;scanf("%d",&x);}return L;
}LinkList List_TailInsert(LinkList L){int x;L = (LinkList)malloc(sizeof(LNode));LinkList s,r = L;scanf("%d",&x);while (x != 9999){s = (LinkList) malloc(sizeof(LNode));s->data = x;r->next = s;r = s;scanf("%d",&x);}r->next = NULL;return L;
}LinkList GetElem(LinkList L,int i){if (i < 1)return NULL;int j = 1;LinkList p = L->next;while(p != NULL && j < i){p = p->next;j ++;}return p;
}LinkList LocateElem(LinkList L,int e){LinkList p = L->next;while (p!=NULL && p->data != e)p = p->next;return p;
}LinkList PreInsert(LinkList L,int i,int e){ //实现在第i个结点之后进行插入LinkList p,s;s = (LinkList) malloc(sizeof(LNode));p = GetElem(L,i-1); //获取第i个结点的前驱结点s->data = e;s->next = p->next;p->next = s;return L;
}LinkList backInsert(LinkList L,int i,int e){LinkList p,s;int temp;s = (LinkList) malloc(sizeof(LNode));p = GetElem(L,i); //获取第i个结点的前驱结点s->data = e;s->next = p->next;p->next = s;temp = p->data;p->data = s->data;s->data = temp;return L;
}//实现删除结点操作的函数的主体如下
LinkList DeleteNode(LinkList L,int i){LinkList p,q;int e;p = GetElem(L,i-1);q = p->next;p->next = q->next;printf("被删除结点的元素的数据为:%d\n",q->data);free(q);return L;
}
和插入算法一样,该算法的主要时间也是耗费在查找操作上,时间复杂度为 O(n)。
7、求表长操作:
求表长操作要求计算单链表数据结点,也就是不含头结点的结点的总个数,需要从第一个结点开始遍历,直到访问完所有的结点,因为比较简单,具体实现就不进行赘述了,不过需要注意:有的链表存在头结点,有的不存在,在计算的时候要做好相关的区分操作。
8、销毁整个表(我自己写的)
不多解释,直接上源码:
void AllFree(LinkList L){LinkList p = L->next,r;while(p){r = p;p = p->next;free(r);}free(p);free(L);
}
2.3.3、双链表:
单链表结点中只有一个指向其后继的指针,使得单链表只能从头结点依次顺序地向后遍历。要访问某个结点的前驱结点(插入、删除操作时),只能从头开始遍历,访问后继结点的时间复杂度为 O(1),访问前驱结点的时间复杂度为 O(n)。
为了克服单链表的上述缺点,引入了双链表,双链表结点中有两个指针 prior 和 next ,分别指向其前驱和后继结点,如下图:

双链表中结点类型的描述如下:
typedef struct DNode{ElemType data;struct DNode *prior,*next;
} Dnode,*DLinkList;
双链表在单链表的结点中增加了一个指向前驱的 prior 指针,因此双链表中的按值查找和按位查找的操作与单链表相同。但双链表在插入和删除操作的实现上,与单链表有着较大的不同。这是因为“链”变化时也需要对 prior 指针做出修改,其关键是保证在修改的过程中不断链。此外,双链表可以很方便地找到其前驱结点,因此,插入、删除操作的时间复杂度仅为 O(1)。
1、双链表的插入操作:
在双链表中 p 所指的结点之后插入结点 *s ,其指针的变化过程如下图:

插入操作的代码如下:
#include "stdio.h"
#include "stdlib.h"typedef struct DNode{int data;struct DNode *prior,*next;
} DNode,*DLinkList;DLinkList create(DLinkList DL);
DLinkList GetElem(DLinkList DL,int i);
DLinkList Insert(DLinkList DL,int i,int e);
void AllFree(DLinkList L);int main(){DLinkList DL,p;DL = create(DL);p = DL->next;while(p){printf("%d,",p->data);p = p->next;}puts("");DL = Insert(DL,3,10);p = DL->next;while(p){printf("%d,",p->data);p = p->next;}AllFree(DL);return 0;
}DLinkList create(DLinkList DL){int x;DL = (DLinkList)malloc(sizeof(DNode));DLinkList s,r = DL;scanf("%d",&x);while (x != 9999){s = (DLinkList) malloc(sizeof(DNode));s->data = x;r->next = s;r->next->prior = r;r = s;scanf("%d",&x);}r->next = NULL;return DL;
}DLinkList GetElem(DLinkList DL,int i){if (i < 1)return NULL;int j = 1;DLinkList p = DL->next;while(p != NULL && j < i){p = p->next;j ++;}return p;
}//实现插入操作的函数主体如下
DLinkList Insert(DLinkList DL,int i,int e){DLinkList s,p;s = (DLinkList) malloc(sizeof(DNode));p = GetElem(DL,i-1);s->data = e;s->next = p->next;p->next->prior = s;s->prior = p;p->next = s;return DL;
}void AllFree(DLinkList DL){DLinkList p = DL->next,r;while(p){r = p;p = p->next;free(r);}free(p);free(DL);
}
2、双链表的删除操作:
删除双链表的结点 *p 的后继结点 *q ,指针变化过程如下图:

删除操作的代码如下:
#include "stdio.h"
#include "stdlib.h"typedef struct DNode{int data;struct DNode *prior,*next;
} DNode,*DLinkList;DLinkList create(DLinkList DL);
DLinkList GetElem(DLinkList DL,int i);
DLinkList Insert(DLinkList DL,int i,int e);
DLinkList Delete(DLinkList DL,int i);
void AllFree(DLinkList L);int main(){DLinkList DL,p;DL = create(DL);p = DL->next;while(p){printf("%d,",p->data);p = p->next;}puts("");DL = Insert(DL,3,10);p = DL->next;while(p){printf("%d,",p->data);p = p->next;}puts("");DL = Delete(DL,3);p = DL->next;while(p){printf("%d,",p->data);p = p->next;}AllFree(DL);return 0;
}DLinkList create(DLinkList DL){int x;DL = (DLinkList)malloc(sizeof(DNode));DLinkList s,r = DL;scanf("%d",&x);while (x != 9999){s = (DLinkList) malloc(sizeof(DNode));s->data = x;r->next = s;r->next->prior = r;r = s;scanf("%d",&x);}r->next = NULL;return DL;
}DLinkList GetElem(DLinkList DL,int i){if (i < 1)return NULL;int j = 1;DLinkList p = DL->next;while(p != NULL && j < i){p = p->next;j ++;}return p;
}DLinkList Insert(DLinkList DL,int i,int e){DLinkList s,p;s = (DLinkList) malloc(sizeof(DNode));p = GetElem(DL,i-1);s->data = e;s->next = p->next;p->next->prior = s;s->prior = p;p->next = s;return DL;
}//实现删除结点的函数的主体
DLinkList Delete(DLinkList DL,int i){DLinkList p,q;q = GetElem(DL,i);p = q->prior;p->next = q->next;q->next->prior = p;free(q);return DL;
}void AllFree(DLinkList DL){DLinkList p = DL->next,r;while(p){r = p;p = p->next;free(r);}free(p);free(DL);
}
2.3.4、循环链表:
1、循环单链表:
循环单链表和单链表的区别在于,表中最后一个结点的指针不是 NULL ,而改为指向头结点,从而整个链表形成一个环,如下图:

在循环单链表中,表尾结点的 next 域指向 L ,故表中没有指针域为 NULL 的结点,因此,循环单链表的判空条件不是头结点的指针是否为空,而是它是否等于头指针。
循环单链表的插入、删除算法与单链表的几乎一样,所不同的是若操作在表尾进行,则执行的操作不同,以让单链表继续保持循环的特性。当然,正因为循环单链表是一个环,因此在任何一个位址上的插入和删除操作都是等价的,无需判断是否是表尾。
在单链表中只能从表头结点开始往后顺序遍历整个链表,而循环单链表可以从表中的任意一个结点开始遍历整个链表。有时对循环链表不设头指针仅设尾指针,以使得操作效率更高。其原因是,若设的是头指针,对在表尾插入元素需要 O(n) 的时间复杂度,而若设的是尾指针 r ,r->next 即为头指针,对在表头或表尾插入元素都只需要 O(1) 的时间复杂度。
2、循环双链表:
由循环单链表的定义不难退出寻你换双链表。不同的是在循环双链表中,头结点的 prior 指针还要指向表尾结点,如下图:

在循环双链表 L 中,某节点 *p 为尾结点时,p->next == L ;当循环双链表为空表时,其头结点的prior 域和 next 域都等于 L 。
2.3.5、静态链表:
静态链表借助数组来描述线性表的链式存储结构,结点也有数据域 data 和 指针域 next ,与之前的链表中的指针不同的是,这里的指针是结点的相对地址(数组下标),又称游标。和顺序表一样,静态链表也要预先分配一段连续的内存空间。
静态链表和单链表的对应关系如下。

静态链表结构类型的描述如下:
#define MaxSize 50
typedef struct {ElemType data;int next;
}SLinkList[MaxSize];
静态链表以 next == 1 作为其结束的标志。静态链表的插入、删除操作与动态链表的相同,只需要修改指针,而不需要移动元素,静态链表没有单链表使用起来方便,但在一些不支持指针的高级语言中,这是一种非常巧妙的设计方法。
相关文章:

数据结构笔记-2、线性表
2.1、线性表的定义和基本操作 如有侵权请联系删除。 2.1.1、线性表的定义: 线性表是具有相同数据类型的 n (n>0) 个数据元素的有限序列,其中 n 为表长,当 n 0 时线性表是一个空表。若用 L 命名线性表,则其一般表示为&am…...

Linux基础IO【II】真的很详细
目录 一.文件描述符 1.重新理解文件 1.推论 2.证明 2.理解文件描述符 1.文件描述符的分配规则 3.如何理解文件操作的本质? 4.输入重定向和输出重定向 1.原理 2.代码实现重定向 3.dup函数 编辑 4.命令行中实现重定向 二.关于缓冲区 1.现象 …...

【C++】模板及模板的特化
目录 一,模板 1,函数模板 什么是函数模板 函数模板原理 函数模板的实例化 推演(隐式)实例化 显示实例化 模板的参数的匹配原则 2,类模板 什么是类模板 类模板的实例化 二,模板的特化 1,类模板的特化 全特化…...
2001-2023年上市公司数字化转型测算数据(含原始数据+处理代码+计算结果)
2001-2023年上市公司数字化转型测算数据(含原始数据处理代码计算结果)(吴非) 1、时间:2001-2023年 2、来源:上市公司年报 3、指标:行业代码、行业名称、证券简称、是否发生ST或ST或PT、是否发生暂停上市…...
ICRA 2024:基于视觉触觉传感器的物体表⾯分类的Sim2Real双层适应⽅法
⼈们通常通过视觉来感知物体表⾯的性质,但有时需要通过触觉信息来补充或替代视觉信息。在机器⼈感知物体属性⽅⾯,基于视觉的触觉传感器是⽬前的最新技术,因为它们可以产⽣与表⾯接触的⾼分辨率 RGB 触觉图像。然⽽,这些图像需要⼤…...
)
代理模式(设计模式)
文章目录 静态代理动态代理代理模式的应用场景动态代理和静态代理的区别 代理模式就是给一个对象提供一个代理,并由代理对象控制对原对象的引用。它使得客户不能直接与真正的目标对象通信。代理对象是目标对象的代表,其他需要与这个目标对象打交道的操作…...

C++函数参数传递
C 函数传参 在C中,函数传递参数的方式主要有三种: 按值传递(pass by value)按引用传递(pass by reference)按指针传递(pass by pointer)。 比较与总结 按值传递:适用…...

软考初级网络管理员_09_网络单选题
1.下列Internet应用中对实时性要求最高的是()。 电子邮件 Web浏览 FTP文件传输 IP电话 2.在Internet中的大多数服务(如WWW、FTP等)都采用()模型。 星型 主机/终端 客户机/服务器 网状 3.子网掩码的作用是()。 可以用来寻找网关 可以区分IP和MAC 可以识别子网 可以…...

曲线拟合 | 二次B样条拟合曲线
B 样条曲线拟合实例:能平滑化曲线 1. 实例1 为MASS包中mcycle数据集。它测试了一系列模拟的交通车事故中,头部的加速度,以此来评估头盔的性能。times为撞击时间(ms),accel为加速度(g)。首先导入数据&#…...

delphi FDMemTable1.SourceView遍历各行数据,取任意行数据无需Next移动指针了。TFDDatSView
for m : 0 to FDMemTable1.SourceView.Rows.Count - 1 do begin if FDMemTable_SP.SourceView.Rows.ItemsI[m].GetData(0) varNull then Continue; end; 9行7列的值。 FDMemTable1.Data.DataView.Rows.ItemsI[9].ValueI[7]; FDMemTable1.Table.Ro…...

为什么选择 ABBYY FineReader PDF ?
帮助用户们对PDF文件进行快速的编辑处理,同时也可以快速识别PDF文件里的文字内容,并且可以让用户们进行文本编辑,所以可以有效提升办公效率。 ABBYY-ABBYY Finereader 15 Win-安装包:https://souurl.cn/OY2L3m 高级转换功能 ABBY…...
php遇到的问题
1、 underfined at line 3 in xxx.php , 错误提示,注释这行代码 // error_reporting(DEBUG ? E_ALL : 0); 目录:config/config.php...
零基础入门学用Arduino 第二部分(二)
重要的内容写在前面: 该系列是以up主太极创客的零基础入门学用Arduino教程为基础制作的学习笔记。个人把这个教程学完之后,整体感觉是很好的,如果有条件的可以先学习一些相关课程,学起来会更加轻松,相关课程有数字电路…...
旅游行业电商平台:数字化转型的引擎与未来发展趋势
引言 旅游行业数字化转型的背景和重要性 随着信息技术的飞速发展,数字化转型成为各行业发展的必然趋势。旅游行业,作为一个高度依赖信息和服务的领域,数字化转型尤为重要。通过数字化手段,旅游行业能够实现资源的高效配置、服务的…...
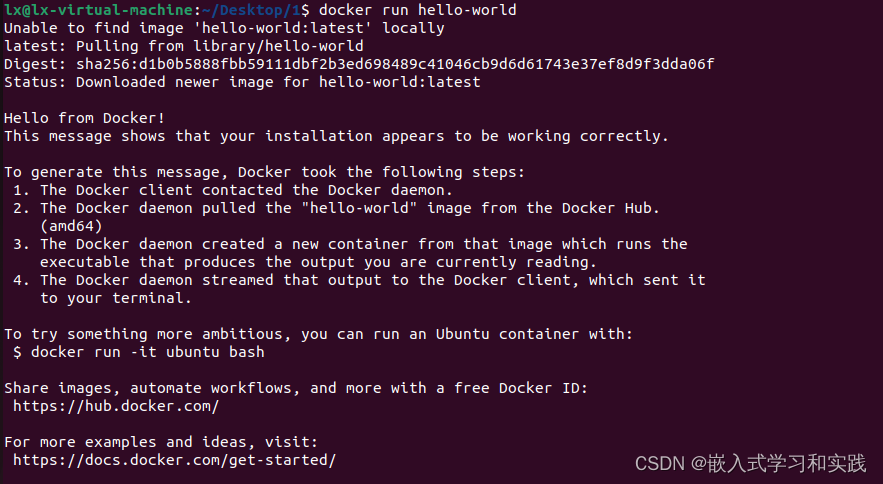
Ubuntu 22.04安装 docker
安装过程和指令 # 1.升级 apt sudo apt update # 2.安装docker sudo apt install docker.io docker-compose # 3.将当前用户加入 docker组 sudo usermod -aG docker ${USER} # 4. 重启 # 5. 查看镜像 docker ps -a 或者 docker images # 6. 下载镜像 docker pull hello-world …...

【Gitlab】访问默认PostgreSQL数据库
本地访问PostgreSQL gitlab有可以直接访问内部PostgreSQL的命令 sudo gitlab-rails dbconsole # 或者 sudo gitlab-psql -d gitlabhq_production效果截图 常用SQL # 查看用户状态 select id,name,email,state,last_sign_in_at,updated_at,last_credential_check_at,last_act…...

乐鑫ESP32-C3芯片应用,启明云端WT32C3-S5模组:简化产品硬件设计
在数字化浪潮的推动下,物联网(IoT)正迅速成为连接现实世界与数字世界的桥梁。芯片作为智能设备的心脏,其重要性不言而喻。 乐鑫推出的ESP32-C3芯片以其卓越的性能和丰富的功能,为智能物联网领域带来了新的活力,我将带您深入了解这…...

算法刷题【二分法】
题目: 注意题目中说明了数据时非递减的,那么这样就存在二分性,能够实现logn的复杂度。二分法每次只能取寻找特定的某一个值,所以我们要分别求左端点和有端点。 分析第一组用例得到结果如下: 成功找到左端点8 由此可知࿰…...
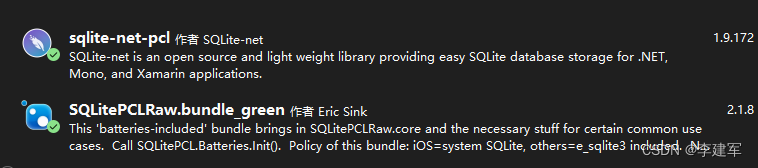
.NET MAUI Sqlite程序应用-数据库配置(一)
项目名称:Ownership(权籍信息采集) 一、安装 NuGet 包 安装 sqlite-net-pcl 安装 SQLitePCLRawEx.bundle_green 二、创建多个表及相关字段 Models\OwnershipItem.cs using SQLite;namespace Ownership.Models {public class fa_rural_base//基础数据…...
基于WPF技术的换热站智能监控系统09--封装水泵对象
1、添加用户控件 2、编写水泵UI 控件中用到了Viewbox控件,Viewbox控件是WPF中一个简单的缩放工具,它可以帮助你放大或缩小单个元素,同时保持其宽高比。通过样式和属性设置,你可以创建出既美观又功能丰富的用户界面。在实际开发中…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
