代码随想录算法训练营第三十九天 | 62.不同路径、63. 不同路径 II、343. 整数拆分、96.不同的二叉搜索树
62.不同路径
题目链接:https://leetcode.cn/problems/unique-paths/
文档讲解:https://programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE…
视频讲解:https://www.bilibili.com/video/BV1ve4y1x7Eu/
思路
- 确定dp数组以及下标的含义:走到第i行第j个格子有
dp[i][j]种方法。 - 确定递推公式:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];因为可以往下走和往右走,所以第i行第j列的点要么是从左边来,要么是从上面来,所以是把这两个格子的方法数相加。 - dp数组如何初始化:初始化第一行和第一列的数据,都只有一种方法可以到达,就是一直往右走或一直往下走。
- 确定遍历顺序:
dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。 - 打印dp数组,用于debug。
代码
class Solution {public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];for (int i = 0; i < m; i++) dp[i][0] = 1;for (int i = 0; i < n; i++) dp[0][i] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
}
分析:时间复杂度:O(m * n),空间复杂度:O(m * n)。
63. 不同路径 II
题目链接:https://leetcode.cn/problems/unique-paths-ii/
文档讲解:https://programmercarl.com/0063.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE…
视频讲解:https://www.bilibili.com/video/BV1Ld4y1k7c6/
思路
- 确定dp数组以及下标的含义:走到第i行第j个格子有
dp[i][j]种方法。 - 确定递推公式:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];因为可以往下走和往右走,所以第i行第j列的点要么是从左边来,要么是从上面来,所以是把这两个格子的方法数相加。但如果这一格有障碍,就为0。 - dp数组如何初始化:本题和上面一道题不以言大哥地方在于本体有障碍,那么初始化的时候,如果遇到了障碍,后面的格子就不可达,为0。
- 确定遍历顺序:
dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。 - 打印dp数组,用于debug。
代码
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length, n = obstacleGrid[0].length;int[][] dp = new int[m][n];for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[0][i] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] != 1) {dp[i][j] = dp[i][j - 1] + dp[i - 1][j];}}}return dp[m - 1][n - 1];}
}
分析:时间复杂度:O(),空间复杂度:O()。
343. 整数拆分
题目链接:https://leetcode.cn/problems/integer-break/
文档讲解:https://programmercarl.com/0343.%E6%95%B4%E6%95%B0%E6%8B%86%E5%88%86.html
视频讲解:https://www.bilibili.com/video/BV1Mg411q7YJ/
思路
- 确定dp数组以及下标的含义:分拆数字i,可以得到的最大乘积为
dp[i]。 - 确定递推公式:从1遍历j,然后有两种渠道得到
dp[i]:- 一个是
j * (i - j)直接相乘。 - 一个是
j * dp[i - j],相当于是拆分(i - j)。 - 最后递推公式为
dp[i] = Math.max(j * (i - j), Math.max(j * dp[i - j], dp[i])); - 在j循环的过程中,会多次计算
dp[i],取最大的。
- 一个是
- dp数组如何初始化:
dp[0]和dp[1]其实是没有意义的,就初始化为0。
dp[0] = 0;
dp[1] = 0;
dp[2] = 1;
- 确定遍历顺序:从前向后遍历。
- 打印dp数组,用于debug
代码
class Solution {public int integerBreak(int n) {int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 0;dp[2] = 1;for (int i = 3; i <= n; i++) {for (int j = 1; j <= i / 2; j++) { // 要拆分成近似相等的数,j大于i的情况就不考虑了dp[i] = Math.max(j * (i - j), Math.max(j * dp[i - j], dp[i]));}}return dp[n];}
}
分析:时间复杂度:O(n2),空间复杂度:O(n)。
96.不同的二叉搜索树
题目链接:https://leetcode.cn/problems/unique-binary-search-trees/
文档讲解:https://programmercarl.com/0096.%E4%B8%8D%E5%90%8C%E7%9A%84%E4%BA%8C%E5%8F%89%E6%90%9C%E7…
视频讲解:https://www.bilibili.com/video/BV1eK411o7QA/
思路
- 确定dp数组以及下标的含义:有i个节点的二叉搜索树有
dp[i]中不同的形状。 - 确定递推公式:确定一个根节点后,这个二叉树的形状数由左右子树形状数量相乘决定,即
dp[i] += dp[j] * dp[i - j - 1];。 - dp数组如何初始化:
dp[0] = 1; dp[1] = 1;,0个节点也算一种形状。 - 确定遍历顺序:从前往后遍历。
- 打印dp数组,用于debug
代码
class Solution {public int numTrees(int n) {int[] dp = new int[n + 1];dp[0] = 1;dp[1] = 1;for (int i = 2; i < dp.length; i++) {for (int j = 0; j < i; j++) {dp[i] += dp[j] * dp[i - j - 1];}}return dp[n];}
}
分析:时间复杂度:O(n2),空间复杂度:O(n)。
相关文章:

代码随想录算法训练营第三十九天 | 62.不同路径、63. 不同路径 II、343. 整数拆分、96.不同的二叉搜索树
62.不同路径 题目链接:https://leetcode.cn/problems/unique-paths/ 文档讲解:https://programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE… 视频讲解:https://www.bilibili.com/video/BV1ve4y1x7Eu/ 思路 确定dp数组以及下标的含…...

C/C++函数指针、C#委托是什么?
函数指针 #include<stdio.h>//声明函数指针 typedef int(*Calc)(int a, int b); int Add(int a, int b) {return a b; } int Sub(int a, int b) {return a - b; }int main() {Calc funcPoint1 &Add;Calc funcPoint2 ⋐int x 120;int y 140;int z 0;z …...

红队攻防渗透技术实战流程:组件安全:JacksonFastJsonXStream
红队攻防渗透实战 1. 组件安全1.1 J2EE-组件Jackson-本地demo&CVE1.1.1 代码执行 (CVE-2020-8840)1.1.2 代码执行(CVE-2020-35728)1.2 J2EE-组件FastJson-本地demo&CVE1.2.1 FastJson <= 1.2.241.2.2 FastJson <= 1.2.471.2.3 FastJson <= 1.2.801.3 J2EE-组…...

Perl 语言学习进阶
一、如何深入 要深入学习Perl语言的库和框架,可以按照以下步骤进行: 了解Perl的核心模块:Perl有许多核心模块,它们提供了许多常用的功能。了解这些模块的功能和用法是深入学习Perl的第一步。一些常用的核心模块包括:S…...

LangGraph实战:从零分阶打造人工智能航空客服助手
❝ 通过本指南,你将学习构建一个专为航空公司设计的客服助手,它将协助用户查询旅行信息并规划行程。在此过程中,你将掌握如何利用LangGraph的中断机制、检查点技术以及更为复杂的状态管理功能,来优化你的助手工具,同时…...

R可视化:R语言基础图形合集
R语言基础图形合集 欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 基础图形可视化 数据分析的图形可视化是了解数据分布、波动和相关性等属性必…...
mysql导入sql文件失败及解决措施
1.报错找不到表 1.1 原因 表格创建失败,编码问题mysql8相较于mysql5出现了新的编码集 1.2解决办法: 使用vscode打开sql文件ctrlh,批量替换,替换到你所安装mysql支持的编码集。 2.timestmp没有设置默认值 Error occured at:20…...

JS:获取鼠标点击位置
一、获取鼠标在目标元素中的点击位置 getClickPos.ts: export const getClickPos (e: MouseEvent) > {return {x: e.offsetX,y: e.offsetY,}; };二、获取鼠标在页面中的点击位置 getClickPos.ts: export const getPageClickPos (e: MouseEvent) > {return {x: e.pa…...
)
使用开源的zip.cpp和unzip.cpp实现压缩包的创建与解压(附源码)
目录 1、使用场景 2、压缩包的创建 3、压缩包的解压 4、CloseZipZ和CloseZipU两接口的区别...

npm 异常:peer eslint@“>=1.6.0 <7.0.0“ from eslint-loader@2.2.1
node 用16版本 npm install npm6.14.15 -g将版本降级到6...
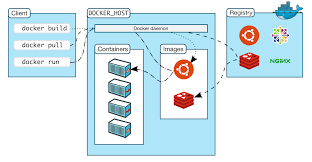
Docker|了解容器镜像层(2)
引言 容器非常神奇。它们允许简单的进程表现得像虚拟机。在这种优雅的底层是一组模式和实践,最终使一切运作起来。在设计的根本是层。层是存储和分发容器化文件系统内容的基本方式。这种设计既出人意料地简单,同时又非常强大。在今天的帖子[1]中…...

使用Python爬取temu商品与评论信息
【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致力于Python与爬虫领域研究与开发工作! 【&…...

mybatis学习--自定义映射resultMap
1.1、resultMap处理字段和属性的映射关系 如果字段名和实体类中的属性名不一致的情况下,可以通过resultMap设置自定义映射。 常规写法 /***根据id查询员工信息* param empId* return*/ Emp getEmpByEmpId(Param("empId") Integer empId);<select id…...
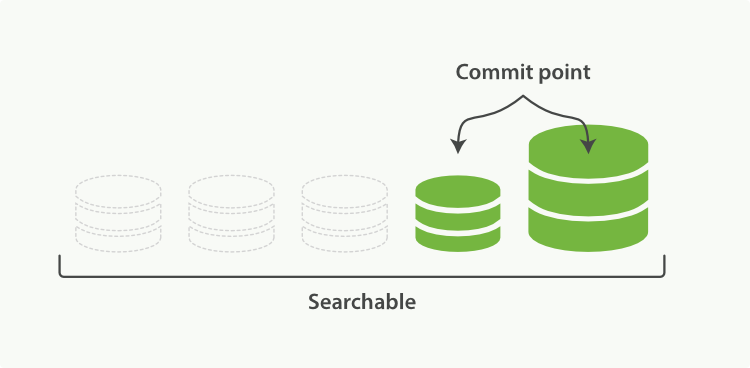
Elasticsearch之写入原理以及调优
1、ES 的写入过程 1.1 ES支持四种对文档的数据写操作 create:如果在PUT数据的时候当前数据已经存在,则数据会被覆盖,如果在PUT的时候加上操作类型create,此时如果数据已存在则会返回失败,因为已经强制指定了操作类型…...

python中装饰器的用法
最近发现装饰器是一个非常有意思的东西,很高级! 允许你在不修改函数或类的源代码的情况下,为它们添加额外的功能或修改它们的行为。装饰器本质上是一个接受函数作为参数的可调用对象(通常是函数或类),并返…...
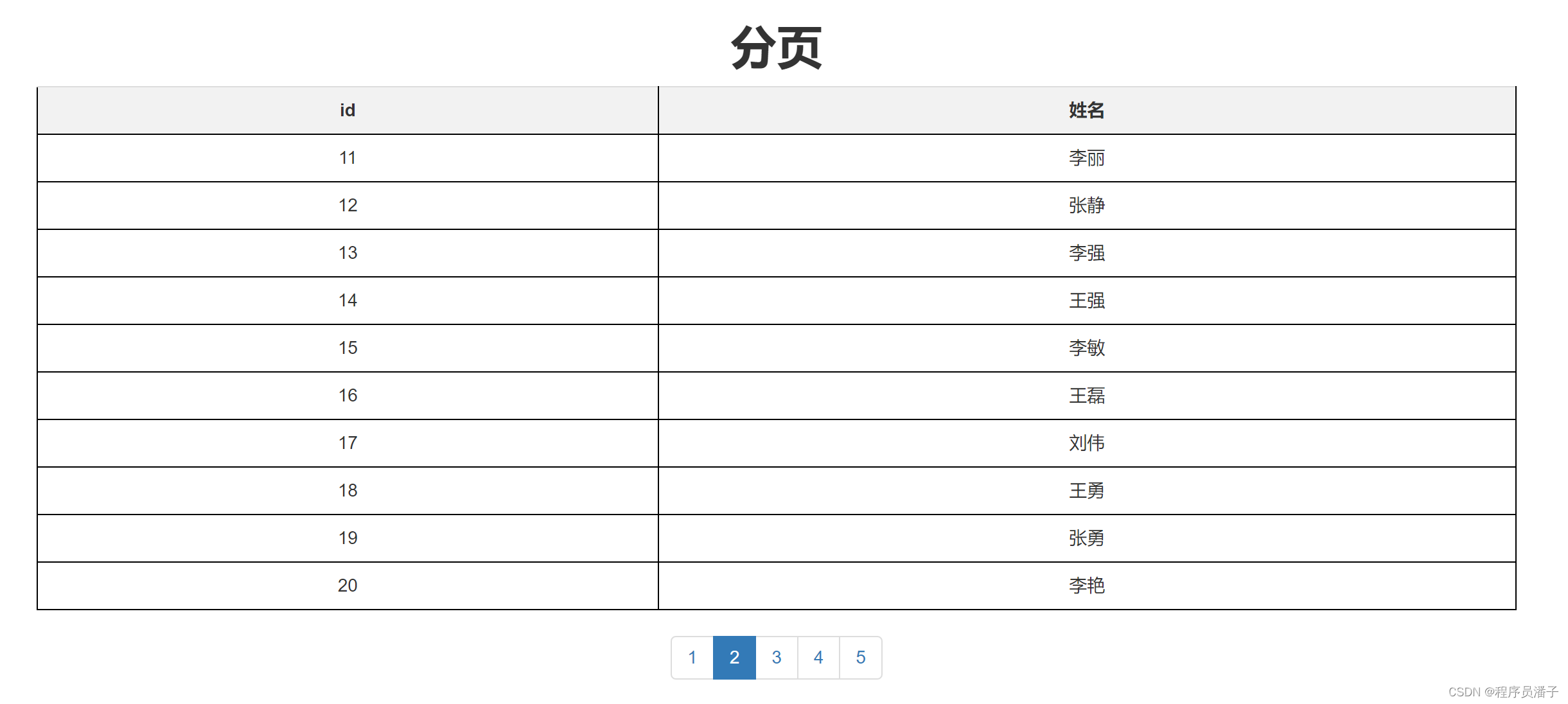
php实现一个简单的MySQL分页
一、案例演示: 二、php 代码 <?php $servername "localhost"; // MySQL服务器名称或IP地址 $username "root"; // MySQL用户名 $password "123456"; // MySQL密码 $dbname "test"; // 要连接…...

算法训练营day23补签
题目1:530. 二叉搜索树的最小绝对差 - 力扣(LeetCode) class Solution { public:int reslut INT_MAX;TreeNode* pre NULL;void trackingback(TreeNode* node) {if(node NULL) return;trackingback(node->left);if(pre ! NULL) {reslut…...

国密SM2JS加密后端解密
1.前端加密 前端加密开源库 sm-crypto 1.1 传统web,下载 sm-crypto 进行打包为 dist/sm2.js 相关打包命令 npm install --save sm-crypto npm install npm run prepublish在web页面引用打包后的文件 <script type"text/javascript" src"<%path %>…...

Cheat Engine.exe修改植物大战僵尸阳光与冷却
Cheat Engine.exe修改植物大战僵尸阳光与冷却 打开Cheat Engine.exe和植物大战僵尸,点CE中文件下面红框位置,选择植物大战僵尸,点击打开 修改冷却: 等冷却完毕,首次扫描0安放植物,再次扫描变动值等冷却完…...
用法)
python内置模块之queue(队列)用法
queue是python3的内置模块,创建堆栈队列,用来处理多线程通信,队列对象构造方法如下: queue.Queue(maxsize0) 是先进先出(First In First Out: FIFO)队列。 入参 maxsize 是一个整数,用于设置…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
