什么是隐马尔可夫模型?
文章目录
- 一、说明
- 二、玩具HMM:5′拼接位点识别
- 三、那么,隐藏了什么?
- 四、查找最佳状态路径
- 五、超越最佳得分对齐
- 六、制作更逼真的模型
- 七、收获
关键词:hidden markov model
一、说明
被称为隐马尔可夫模型的统计模型是计算生物学中反复出现的主题。什么是隐马尔可夫模型,为什么它们对这么多不同的问题如此有用?
通常,生物序列分析只是在每个残留物上贴上正确的标签。在基因鉴定中,我们希望将核苷酸标记为外显子、内含子或基因间序列。在序列比对中,我们希望将查询序列中的残基与目标数据库序列中的同源残基相关联。我们总是可以为任何给定的问题编写一个临时程序,但同样令人沮丧的问题总是会反复出现。一是我们希望整合异构的信息来源。例如,基因发现者应该将剪接位点共识、密码子偏差、外显子/内含子长度偏好和开放阅读框分析结合到一个评分系统中。这些参数应该如何设置?应该如何对不同类型的信息进行加权?第二个问题是从概率上解释结果。找到最佳得分答案是一回事,但分数意味着什么,我们对最佳得分答案是否正确的信心有多大?第三个问题是可扩展性。当我们完善我们的临时基因发现器时,我们希望我们也模拟了翻译起始共识、选择性剪接和多聚腺苷酸化信号。很多时候,将更多的现实堆积在一个脆弱的临时程序上,会使它在自身的重量下崩溃。
隐马尔可夫模型 (HMM) 是建立线性序列“标记”问题的概率模型的形式基础1,2.它们提供了一个概念工具包,只需绘制直观的图片即可构建复杂的模型。它们是各种项目的核心,包括基因查找、图谱搜索、多序列比对和调控位点鉴定。HMM 是计算序列分析的乐高积木。
二、玩具HMM:5′拼接位点识别
举个简单的例子,想象一下下面一个 5’ 剪接位点识别问题的漫画。假设我们得到一个 DNA 序列,该序列从外显子exon开始,包含一个 5’ 剪接位点,以内含子intron结束。问题在于确定从外显子到内含子的转换发生在哪里——5′剪接位点(5′SS)在哪里。
为了让我们智能地猜测,外显子、剪接位点和内含子的序列必须具有不同的统计特性。让我们想象一些简单的差异:假设外显子平均具有均匀的碱基组成(每个碱基 25%),内含子富含 A/T(例如,A/T 各 40%,C/G 各 10%),5′SS 共有核苷酸几乎总是 G(例如,95% G 和 5% A)。
从这些信息开始,我们可以绘制一个 HMM(图 1)。HMM 调用三种状态,一种状态对应我们可能分配给核苷酸的三个标签:E(exon)、5(5′SS)和 I(intron)。每个状态都有自己的发射概率(如上所示),它模拟了 5′SS 处外显子、内含子和共识 G 的基本组成。每个状态也有转换概率(箭头),即从这个状态移动到新状态的概率。转移概率描述了我们期望状态发生的线性顺序:一个或多个 E、一个 5、一个或多个 I。
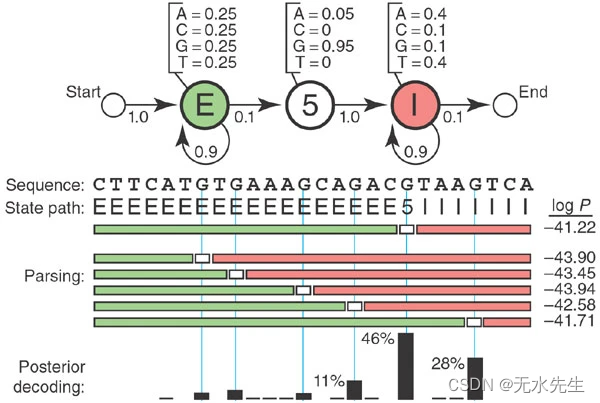
图 1:用于 5’ 剪接位点识别的玩具 HMM。
三、那么,隐藏了什么?
想象一个 HMM 生成一个序列是很有用的。当我们访问一个州时,我们会从该州的排放概率分布中排放出残留物。然后,我们根据该州的转移概率分布选择接下来要访问的州。因此,该模型生成了两串信息。一个是基础状态路径(标签),当我们从一个状态转换到另一个状态时。另一个是观察到的序列(DNA),每个残基都从状态路径中的一个状态发射出来。
状态路径是马尔可夫链,这意味着我们接下来要进入的状态仅取决于我们所处的状态。由于我们只得到了观察到的序列,所以这个底层状态路径是隐藏的——这些是我们想要推断的残基标签。状态路径是一条隐藏的马尔可夫链。
概率 P(S,π|HMM,θ),具有参数 θ 的 HMM 生成状态路径 π,观测到的序列 S 是所使用的所有发射概率和跃迁概率的乘积。例如,考虑图 1 中间的 26 个核苷酸序列和状态路径,其中有 27 个跃迁和 26 个发射需要处理。将所有 53 个概率相乘(并取对数,因为这些数字很小),您将计算对数 P(S,π|HMM,θ) = −41.22。
HMM 是一个完全概率模型——模型参数和整体序列“分数”都是概率。因此,我们可以使用贝叶斯概率论以标准、强大的方式操纵这些数字,包括优化参数和解释分数的重要性。
四、查找最佳状态路径
在分析问题中,我们得到了一个序列,我们想要推断隐藏的状态路径。可能有许多状态路径可以生成相同的序列。我们想找到概率最高的那个。
例如,如果我们在图 1 中给定 HMM 和 26 个核苷酸序列,则有 14 条可能的路径具有非零概率,因为 5′SS 必须落在 14 个内部 As 或 G 之一上。最好的一个的对数概率为 −41.22,这推断出最有可能的 5′SS 位置位于第五个 G。
对于大多数问题,有太多可能的状态序列,我们无法枚举它们。高效的 Viterbi 算法保证在给定序列和 HMM 的情况下找到最可能的状态路径。维特比算法是一种动态规划算法,与用于标准序列比对的算法非常相似。
五、超越最佳得分对齐
图 1 显示,一个替代状态路径与将 5′SS 置于第五个 G 的分数略有不同(对数概率为 -41.71 对 -41.22)。我们对第五个G是正确的选择有多大信心?
这是概率建模优势的一个例子:我们可以直接计算我们的置信度。状态 k 发出残基 i 的概率是使用状态 k 生成残基 i(即 π我 = k 在状态路径 π) 中,由所有可能的状态路径的总和归一化。在我们的玩具模型中,这只是分子中的一条状态路径和分母中 14 条状态路径的总和。我们得到得分最高的第五个 G 正确率为 46%,第六个 G 位置正确率为 28%(图 1,底部)。这称为后验解码。对于较大的问题,后验解码使用两种称为“前向”和“后向”的动态规划算法,它们本质上类似于 Viterbi,但它们对可能的路径求和,而不是选择最佳路径。
六、制作更逼真的模型
制作 HMM 意味着指定四件事:(i) 符号字母表,K 个不同的符号(例如,ACGT,K = 4); (ii)模型中的状态数,M;(iii) 排放概率 e我(x) 对于每个状态 i,该总和 1 超过 K 符号 x, Σxe我(x) = 1;(iv)转移概率t我(j) 对于每个状态 i 到任何其他状态 j(包括它自己),其总和为 1 超过 M 状态 j, Σjt我(j) = 1。任何具有这些属性的模型都是 HMM。
这意味着只需绘制与手头问题相对应的图片即可制作新的 HMM,如图 1 所示。这种图形的简单性使人们可以清楚地关注问题的生物学定义。
例如,在我们的玩具拼接站点模型中,也许我们对自己的辨别能力不满意;也许我们想在 5’ 剪接位点添加一个更现实的六核苷酸共识 GTRAGT。我们可以用一行六个 HMM 状态代替“5”状态,以模拟一个六碱基无固定的共识基序,参数化已知 5’ 剪接位点的发射概率。也许我们想模拟一个完整的内含子,包括一个 3’ 剪接位点;我们只需为 3′SS 共识添加一行状态,并添加一个 3′ 外显子状态,让观察到的序列以外显子而不是内含子结束。那么也许我们想建立一个完整的基因模型…无论我们添加什么,都只是画出我们想要的东西。
七、收获
HMM 不能很好地处理残基之间的相关性,因为它们假设每个残基仅取决于一种基础状态。HMM 通常不合适的一个例子是 RNA 二级结构分析。保守的RNA碱基对诱导长程成对相关性;一个位置可能是任何残基,但碱基配对的伴侣必须是互补的。HMM 状态路径无法“记住”遥远状态生成的内容。
有时,人们可以在不破坏算法的情况下弯曲 HMM 的规则。例如,在基因发现中,人们想要发射一个相关的三重密码子,而不是三个独立的残基;HMM 算法可以很容易地扩展到三重态发射态。但是,基本的 HMM 工具包只能延伸到此为止。除了HMM之外,还有更强大(尽管效率较低)的概率模型用于序列分析。
相关文章:

什么是隐马尔可夫模型?
文章目录 一、说明二、玩具HMM:5′拼接位点识别三、那么,隐藏了什么?四、查找最佳状态路径五、超越最佳得分对齐六、制作更逼真的模型七、收获 关键词:hidden markov model 一、说明 被称为隐马尔可夫模型的统计模型是计算生物学…...

qt中使用qsqlite连接数据库,却没有在本地文件夹中生成db文件
exe运行起来之后,发现没有在exe文件夹下生成数据库文件,,之前可以,但中间莫名其妙不行了,代码如下 // 建立和SQlite数据库的连接database QSqlDatabase::addDatabase("QSQLITE");// 设置数据库文件的名字da…...

Django的‘通用视图TemplateView’
使用通用视图的好处是:如果有一个html需要展示,不需要写view视图函数,直接写好url即可。 使用通用视图的步骤如下: 1、编辑项目urls.py文件 from django.views.generic import TemplateView 在该文件的映射表中添加:…...

java功能实现在某个时间范围之内输出true,不在某个范围输出false,时间精确到分钟
import org.slf4j.Logger; import org.slf4j.LoggerFactory; public class DateTimeChecker { private static final Logger log LoggerFactory.getLogger(DateTimeChecker.class); /** * 检查当前时间是否在指定的小时和分钟范围内。 * * param startHour 开…...
macbook屏幕录制技巧,这2个方法请你收好
在当今数字化时代,屏幕录制成为了一项不可或缺的技能,无论是教学演示、游戏直播,还是软件操作教程,屏幕录制都能帮助我们更直观地传达信息。MacBook作为苹果公司的标志性产品,其屏幕录制功能也备受用户关注。本文将详细…...

vue-loader
Vue Loader 是一个 webpack 的 loader,它允许你以一种名为单文件组件 (SFCs)的格式撰写 Vue 组件 起步 安装 npm install vue --save npm install webpack webpack-cli style-loader css-loader html-webpack-plugin vue-loader vue-template-compiler webpack…...

IO系列(十) -TCP 滑动窗口原理介绍(上)
一、摘要 之前在上分享网络编程知识文章的时候,有网友写下一条留言:“可以写写一篇关于 TCP 滑动窗口原理的文章吗?”。 当时没有立即回复,经过查询多方资料,发现这个 TCP 真的非常非常的复杂,就像一个清…...

IPython 使用技巧整理
IPython 是一个增强的 Python 交互式 shell,提供了许多实用的功能和特性,使得 Python 编程和数据科学工作变得更加便捷和高效。以下是一些 IPython 的使用技巧整理: 1. 自动补全和查询 Tab 补全:在 IPython 中,你可以…...

Python 引入中文py文件
目录 背景 思路 importlib介绍 使用方法 1.导入内置库 importlib.util 2.创建模块规格对象 spec importlib.util.spec_from_file_location("example_module", "example.py") 3.创建模块对象 module importlib.util.module_from_spec(spec) …...
qt 实现模拟实际物体带速度的移动(水平、垂直、斜角度)——————附带完整代码
文章目录 0 效果1 原理1.1 图片旋转1.2 物体按照现实中的实际距离带真实速度移动 2 完整实现2.1 将车辆按钮封装为一个类:2.2 调用方法 3 完整代码参考 0 效果 实现后的效果如下 可以显示属性(继承自QToolButton): 鼠标悬浮显示文字 按钮…...
驱动开发(三):内核层控制硬件层
驱动开发系列文章: 驱动开发(一):驱动代码的基本框架 驱动开发(二):创建字符设备驱动 驱动开发(三):内核层控制硬件层 ←本文 目录…...

企业邮箱大附件无法上传?无法确认接收状态?这样解决就行
Outlook邮箱作为最常用的邮箱系统,被全世界企业采用作为内部通用沟通方式,但Outlook邮箱却有着明显的使用缺陷,如邮箱大附件上传障碍及附件接收无提示等。 1、企业邮箱大附件无法上传 Outlook企业邮箱大附件的上传上限一般是50M,…...
)
Kotlin 数据类(Data Class)
Kotlin 数据类(Data Class)是一种特别用于持有数据的类。它们简化了数据类的创建,并提供了一些自动生成的方法。下面详细介绍 Kotlin 数据类的原理和使用方法。 数据类的定义 Kotlin 中的数据类使用 data 关键字定义。例如: da…...
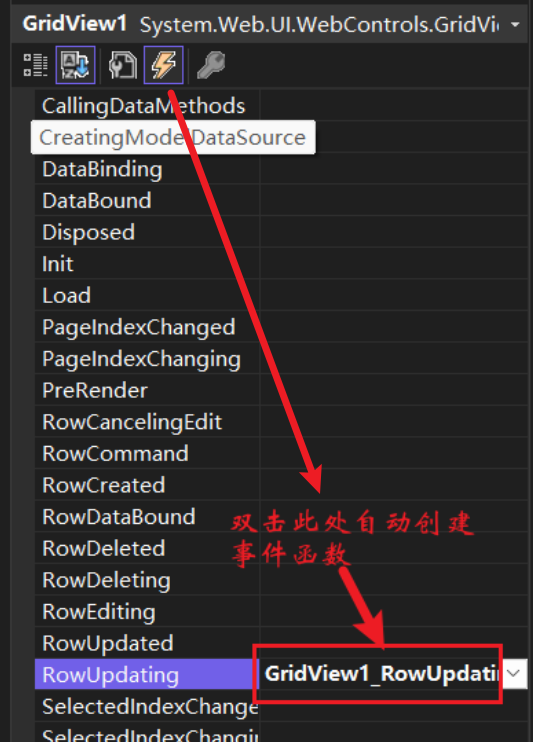
gridview自带编辑功能如何判断用户修改的值的合法性
在使用GridView的编辑功能更新值时,确保输入的值合法性是十分重要的。为了实现这一点,你可以在GridView的RowUpdating事件中加入代码来检查用户输入的值。如果发现输入的值不合法,你可以取消更新操作并向用户显示错误消息。下面是如何实现的步…...
设计模式-结构型-06-桥接模式
1、传统方式解决手机操作问题 现在对不同手机类型的不同品牌实现操作编程(比如:开机、关机、上网,打电话等),如图: UML 类图 问题分析 扩展性问题(类爆炸):如果我们再…...

安泰电压放大器的选型原则是什么
电压放大器是电子电路中常用的一种器件,主要用于放大输入电压信号。在选型电压放大器时,需要考虑以下几个原则。 根据应用需求确定放大倍数。放大倍数是指输出电压与输入电压之间的倍数关系,也称为增益。不同的应用场景对放大倍数的要求不同&…...

方法分享 |公网IP怎么指定非433端口实现https访问
公网IP可以通过指定非443端口实现HTTPS访问。在网络配置中,虽然HTTPS协议默认使用443端口,但没有规定不能在其他端口上实施HTTPS服务。使用非标准端口进行HTTPS通信需要正确配置服务器和SSL证书,并确保客户端能够连接到指定的端口。下面说明如…...
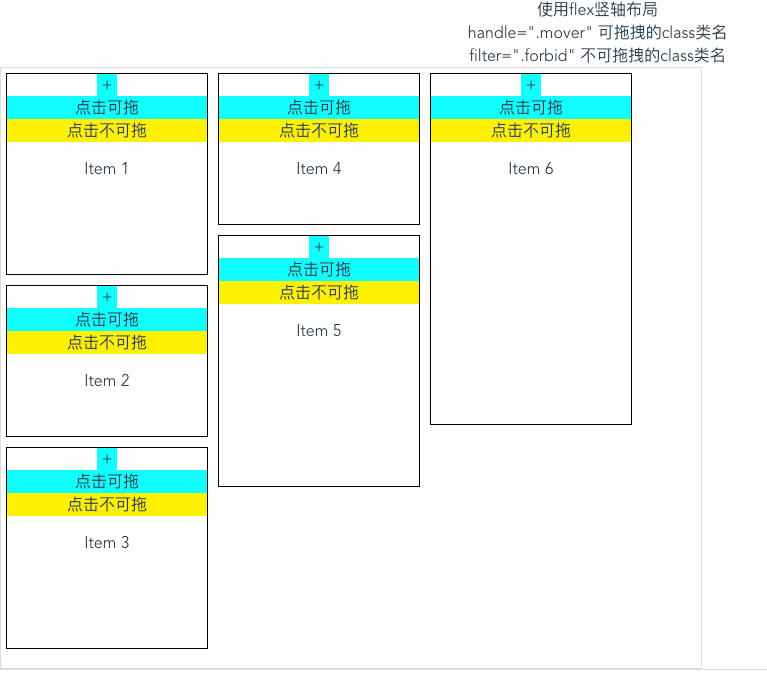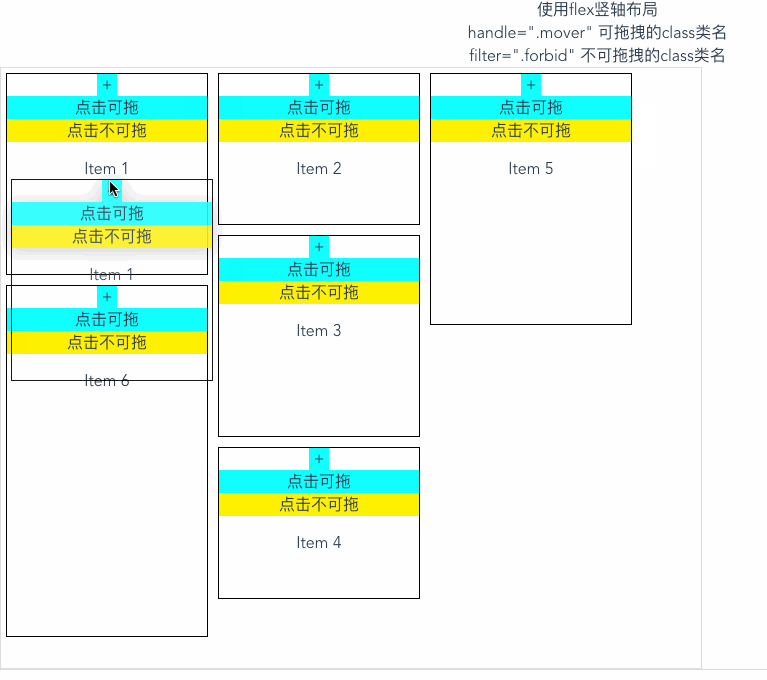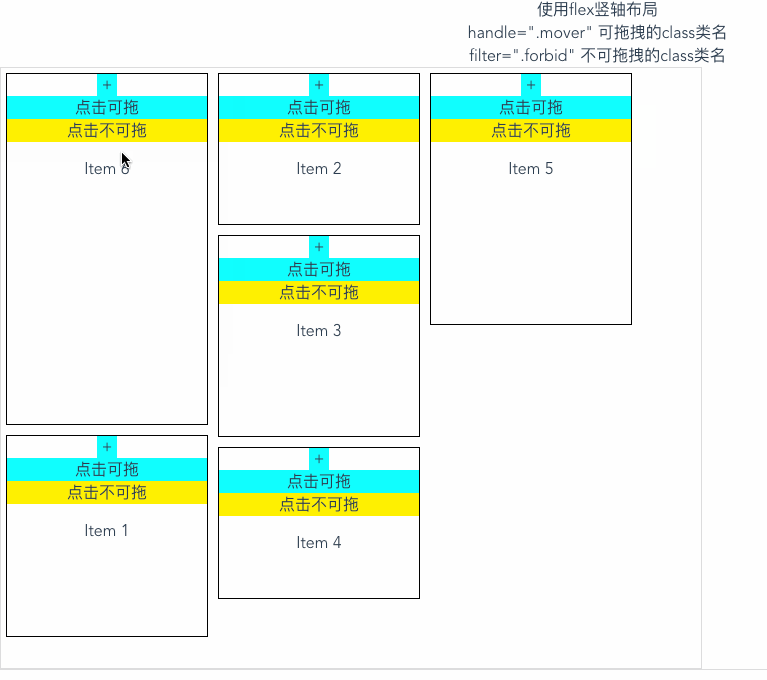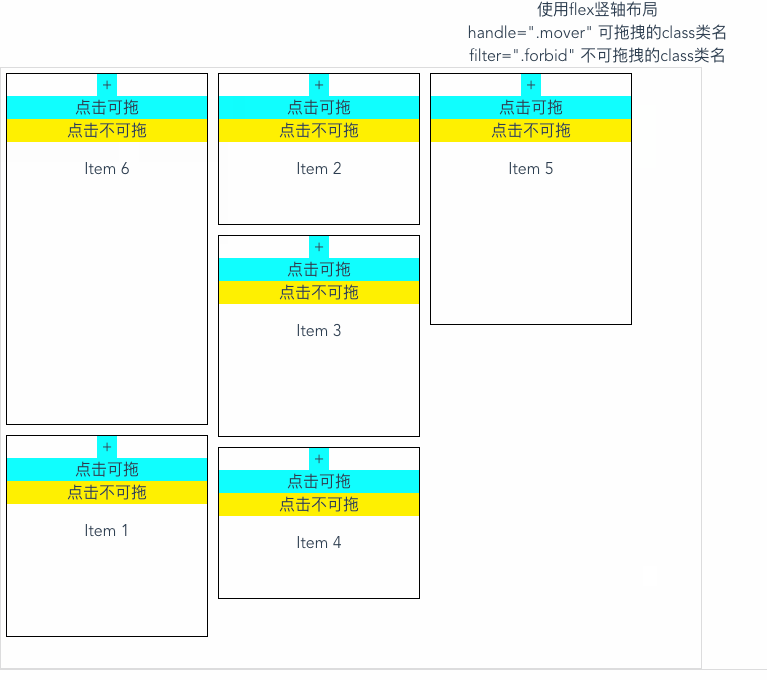
vue实现拖拽元素;vuedraggable拖拽插件
效果图: 中文文档 以下代码可直接复制使用 安装依赖 npm i -S vuedraggable使用 <template><div class"container"><div>使用flex竖轴布局 <br>handle".mover" 可拖拽的class类名 <br>filter".forbid&qu…...

Javascript介绍
Javascript 定义:一门简单的浏览器可解析的语言 作用:与HTML相结合使用,使我们的网页变得更加酷炫 发展史: 1.1992年,Nombase公司开发出来,校验表单,起名c--,后来更名为&#…...
毕业答辩PPT:如何在短时间内高效准备?
提起PPT,大家的第一反应就是痛苦。经常接触PPT的学生党和打工人,光看到这3个字母,就已经开始头痛了: 1、PPT内容框架与文案挑战重重,任务艰巨,耗费大量精力。 2、PPT的排版技能要求高,并非易事…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
