数据分析必备:一步步教你如何用matplotlib做数据可视化(10)
1、Matplotlib 二维箭头图
箭头图将速度矢量显示为箭头,其中分量(u,v)位于点(x,y)。
quiver(x,y,u,v)
上述命令将矢量绘制为在x和y中每个对应元素对中指定的坐标处的箭头。
参数
下表列出了quiver()函数的参数 -
x - 1D或2D阵列,序列。箭头位置的x坐标
y - 1D或2D阵列,序列。箭头位置的y坐标
u - 1D或2D阵列,序列。箭头矢量的x分量
v - 1D或2D阵列,序列。箭头矢量的y分量
c - 1D或2D阵列,序列。箭头位置的x坐标
以下代码绘制了一个简单的箭袋图
import matplotlib.pyplot as plt
import numpy as np
import math
import seaborn as sns
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一(替换sans-serif字体)
plt.rcParams['axes.unicode_minus'] = False # 原文出自【立地货】,商业转载请联系作者获得授权,非商业请保留原文链接:
x,y = np.meshgrid(np.arange(-2, 2, .2), np.arange(-2, 2, .25))
z = x*np.exp(-x**2 - y**2)
v, u = np.gradient(z, .2, .2)
fig, ax = plt.subplots()
q = ax.quiver(x,y,u,v)
plt.show()
执行上面示例代码,得到以下结果
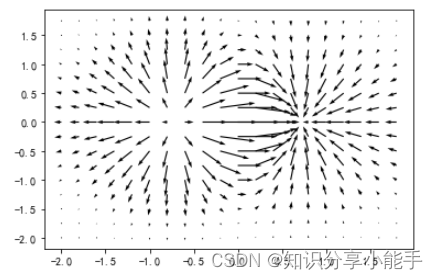
2、Matplotlib 箱线图
箱形图也称为须状图,显示包含最小值,第一四分位数,中位数,第三四分位数和最大值的一组数据的摘要。在方块图中,绘制从第一个四分位数到第三个四分位数的方框。垂直线穿过中间的框。须状从每个四分位数到最小值或最大值。
执行代码结果
让我们为箱形图创建数据。使用numpy.random.normal()函数来创建虚假数据。它需要三个参数,正态分布的均值和标准差,以及所需的值的数量。
np.random.seed(10)
collectn_1 = np.random.normal(100, 10, 200)
collectn_2 = np.random.normal(80, 30, 200)
collectn_3 = np.random.normal(90, 20, 200)
collectn_4 = np.random.normal(70, 25, 200)
上面创建的数组列表是创建boxplot所需的唯一输入。使用data_to_plot代码行,可以使用以下代码创建boxplot
fig = plt.figure()
#创建轴实例
ax = fig.add_axes([0,0,1,1])
#创建箱线图
bp = ax.boxplot(data_to_plot)
plt.show()
执行上面的代码行将生成以下输出
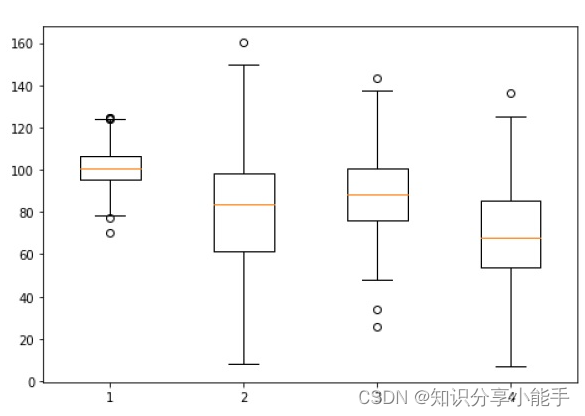
3、Matplotlib 小提琴图
小提琴图类似于箱形图,除了它们还显示不同值的数据的概率密度。这些图包括数据中位数的标记和表示四分位数范围的框,如标准框图中所示。在该箱图上叠加的是核密度估计。与箱形图一样,小提琴图用于表示跨不同“类别”的可变分布(或样本分布)的比较。
小提琴图形比普通图形更具信息性。事实上,虽然箱形图仅显示平均值/中位数和四分位数范围等汇总统计量,但小提琴图显示了数据的完整分布。
import matplotlib.pyplot as plt
np.random.seed(10)
collectn_1 = np.random.normal(100, 10, 200)
collectn_2 = np.random.normal(80, 30, 200)
collectn_3 = np.random.normal(90, 20, 200)
collectn_4 = np.random.normal(70, 25, 200)
##将这些不同的集合合并到一个列表中
data_to_plot = [collectn_1, collectn_2, collectn_3, collectn_4]
#创建一个图形实例
fig = plt.figure()
#创建轴实例
ax = fig.add_axes([0,0,1,1])
#创建箱线图
bp = ax.violinplot(data_to_plot)
plt.show()
执行上面示例代码,得到以下结果

相关文章:

数据分析必备:一步步教你如何用matplotlib做数据可视化(10)
1、Matplotlib 二维箭头图 箭头图将速度矢量显示为箭头,其中分量(u,v)位于点(x,y)。 quiver(x,y,u,v)上述命令将矢量绘制为在x和y中每个对应元素对中指定的坐标处的箭头。 参数 下表列出了quiver()函数的参数 - x - 1D或2D阵列,…...
Stable Diffusion部署教程,开启你的AI绘图之路
本文环境 系统:Ubuntu 20.04 64位 内存:32G 环境安装 2.1 安装GPU驱动 在英伟达官网根据显卡型号、操作系统、CUDA等查询驱动版本。官网查询链接https://www.nvidia.com/Download/index.aspx?langen-us 注意这里的CUDA版本,如未安装CUD…...

三生随记——诡异的牙线
在小镇的角落,坐落着一间古老的牙医诊所。这所诊所早已荒废多年,窗户上爬满了藤蔓,门板上的油漆斑驳脱落,仿佛诉说着无尽的沉寂与孤独。然而,在午夜时分,偶尔会有低沉的呻吟声从紧闭的诊所里传出࿰…...
批量重命名神器揭秘:一键实现文件夹随机命名,自定义长度轻松搞定!
在数字化时代,我们经常需要管理大量的文件夹,尤其是对于那些需要频繁更改或整理的文件来说,给它们进行批量重命名可以大大提高工作效率。然而,传统的重命名方法既繁琐又耗时,无法满足高效工作的需求。今天,…...
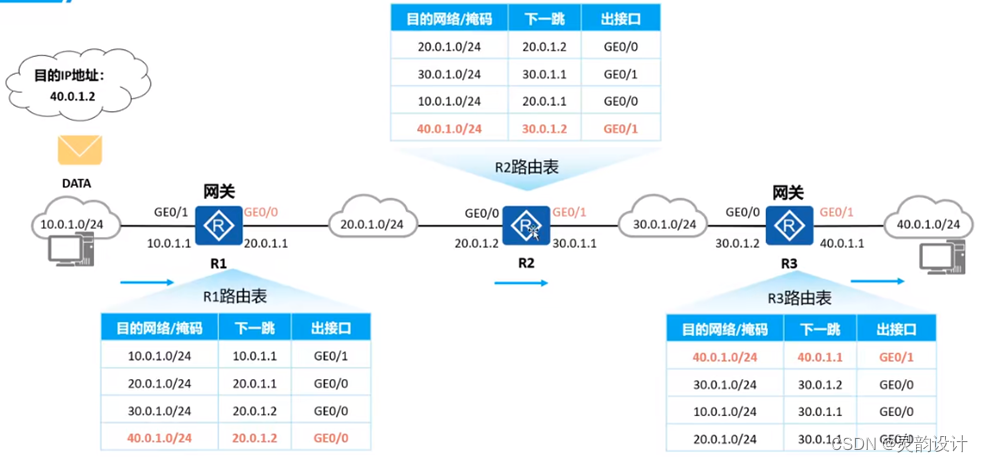
学习笔记——路由网络基础——路由转发
六、路由转发 1、最长匹配原则 最长匹配原则 是支持IP路由的设备默认的路由查找方式(事实上几乎所有支持IP路由的设备都是这种查找方式)。当路由器收到一个IP数据包时,会将数据包的目的IP地址与自己本地路由表中的表项进行逐位(Bit-By-Bit)的逐位查找,…...

Python网络安全项目开发实战,如何防命令注入
注意:本文的下载教程,与以下文章的思路有相同点,也有不同点,最终目标只是让读者从多维度去熟练掌握本知识点。 下载教程: Python网络安全项目开发实战_防命令注入_编程案例解析实例详解课程教程.pdf 在Python网络安全项目开发中,防止命令注入(Command Injection)是一项…...

程序员如何高效读代码?
程序员高效读代码的技巧包括以下几点: 明确阅读目的:在开始阅读代码之前,先明确你的阅读目的。是为了理解整个系统的架构?还是为了修复一个具体的bug?或者是为了了解某个功能是如何实现的?明确目的可以帮助…...

全面分析一下前端框架Angular的来龙去脉,分析angular的技术要点和难点,以及详细的语法和使用规则,底层原理-小白进阶之路
Angular 前端框架全面分析 Angular 是一个由 Google 维护的开源前端框架。它最早在 2010 年发布,最初版本称为 AngularJS。2016 年,团队发布了一个完全重写的版本,称为 Angular 2,之后的版本(如 Angular 4、Angular 5…...

VACUUM 剖析
VACUUM 剖析 为什么需要 Vacuum MVCC MVCC:Multi-Version Concurrency Control,即多版本并发控制。 PostgreSQL 使用多版本并发控制(MVCC)来支持高并发的事务处理,同时保持数据的一致性和隔离性。MVCC 是一种用于管…...

基于LangChain框架搭建知识库
基于LangChain框架搭建知识库 说明流程1.数据加载2.数据清洗3.数据切分4.获取向量5.向量库保存到本地6.向量搜索7.汇总调用 说明 本文使用openai提供的embedding模型作为框架基础模型,知识库的搭建目的就是为了让大模型减少幻觉出现,实现起来也很简单&a…...

LeetCode 1789, 6, 138
目录 1789. 员工的直属部门题目链接表要求知识点思路代码 6. Z 字形变换题目链接标签思路代码 138. 随机链表的复制题目链接标签思路代码 1789. 员工的直属部门 题目链接 1789. 员工的直属部门 表 表Employee的字段为employee_id,department_id和primary_flag。…...

Redis部署模式全解析:单点、主从、哨兵与集群
Redis是一个高性能的键值存储系统,以其丰富的数据结构和优异的读写性能而闻名。在实际应用中,根据业务需求的不同,Redis可以部署在多种模式下。本文将详细介绍Redis的四种主要部署模式:单点模式、主从复制模式、哨兵模式以及集群模…...

python-docx顺序读取word内容
来源How to use Python iteration to read paragraphs, tables and pictures in word? Issue #650 python-openxml/python-docx (github.com) from docx import Document from docx.oxml.ns import qndef iter_block_items(parent):"""生成 paren…...
)
kafka 集群原理设计和实现概述(一)
kafka 集群原理设计和实现概述(一) Kafka 集群的设计原理是为了实现高可用性、高吞吐量、容错性和可扩展性。以下是 Kafka 集群的设计原 理及其实现方法: 1. 分布式架构设计 Kafka 采用分布式架构,集群中的多个 Broker 共同工作,负责接收、存储和传递消息。通过将数据分布…...

three.js 第十一节 - uv坐标
// ts-nocheck // 引入three.js import * as THREE from three // 导入轨道控制器 import { OrbitControls } from three/examples/jsm/controls/OrbitControls // 导入lil.gui import { GUI } from three/examples/jsm/libs/lil-gui.module.min.js // 导入tween import * as T…...

git从master分支创建分支
1. 切换到主分支或你想从哪里创建新分支 git checkout master 2. 创建并切换到新的本地分支 develop git checkout -b develop 3. 将新分支推送到远程存储库 git push origin develop 4. 设置本地 develop 分支跟踪远程 develop 分支 git branch --set-upstream-toorigi…...
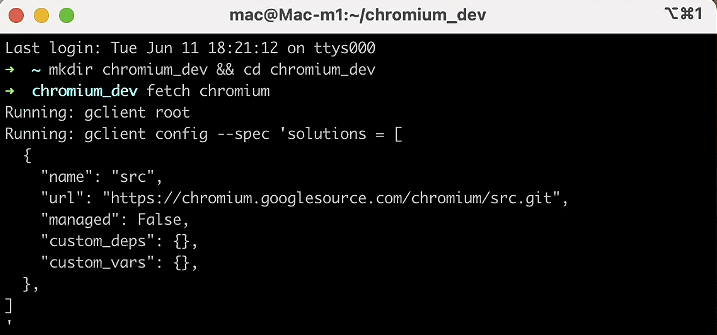
Chromium 调试指南2024 Mac篇 - 准备工作 (一)
1.引言 Chromium是一个由Google主导开发的开源浏览器项目,它为Google Chrome浏览器提供了基础框架。Chromium不仅是研究和开发现代浏览器技术的重要平台,还为众多其他基于Chromium的浏览器(如Microsoft Edge、Brave等)提供了基础…...
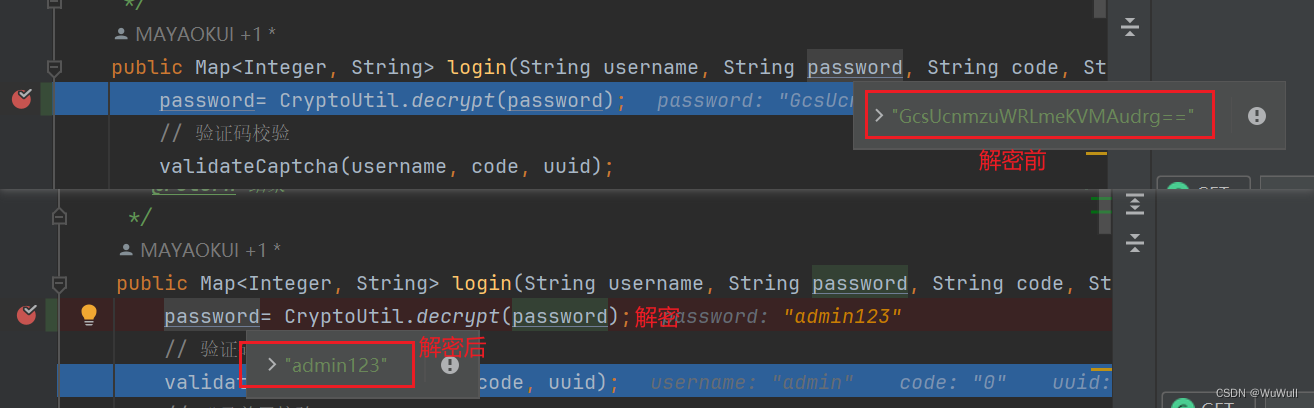
vue登陆密码加密,java后端解密
前端 安装crypto-js npm install crypto-js加密 //引入crypto-js import CryptoJS from crypto-js;/** ---密码加密 start--- */ const SECRET_KEY CryptoJS.enc.Utf8.parse("a15q8f6s5s1a2v3s"); const SECRET_IV CryptoJS.enc.Utf8.parse("a3c6g5h4v9sss…...
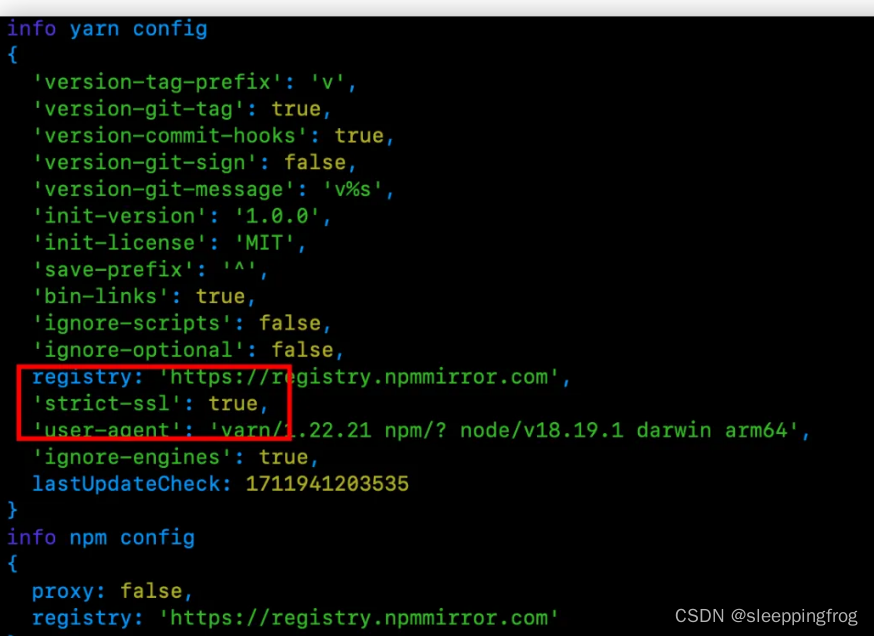
npm 安装踩坑
1 网络正常,但是以前的老项目安装依赖一直卡住无法安装?哪怕切换成淘宝镜像 解决办法:切换成yarn (1) npm i yarn -g(2) yarn init(3) yarn install在安装的过程中发现: [2/4] Fetching packages... error marked11.1.0:…...

内容安全复习 6 - 白帽子安全漏洞挖掘披露的法律风险
文章目录 安全漏洞的法律概念界定安全漏洞特征白帽子安全漏洞挖掘面临的法律风险“白帽子”安全漏洞挖掘的风险根源“白帽子”的主体边界授权行为边界关键结论 安全漏洞的法律概念界定 可以被利用来破坏所在系统的网络或信息安全的缺陷或错误;被利用的网络缺陷、错…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
