408数据结构-图的应用1-最小生成树 自学知识点整理
前置知识:图的遍历
图的应用是408初试历年考查的重点。不过一般而言,这部分内容直接以算法设计题形式考查的可能性极小,更多的是结合图的实例来考查算法的具体操作过程,要求掌握的是手推模拟给定图的各个算法执行过程。此外,还需对给定模型建立相应的图去解决问题。
最小生成树
知识点回顾:图的基本概念-生成树
一个连通图的生成树包含图的所有顶点,并且只含尽可能少的边。对于生成树来说,若砍去(减少)它的一条边,则会使生成树变成非连通图;若给它增加一条边,则会形成图中的一条回路(环)。
对于一个带权连通无向图 G G G,生成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。权值之和最小的那棵生成树称为 G G G的最小生成树( M i n i m u m − S p a n n i n g − T r e e Minimum-Spanning-Tree Minimum−Spanning−Tree, M S T MST MST)。
最小生成树的性质
- 若图 G G G中存在权值相同的边,则 G G G的最小生成树可能不唯一,即最小生成树的树形可能不唯一。当图 G G G中的各边权值互不相等时, G G G的最小生成树是唯一的;若无向连通图 G G G的边数比顶点数少 1 1 1,即 G G G本身是一棵树时,则图 G G G的最小生成树就是其本身;只有连通图才有生成树,非连通图只有生成森林。
- 虽然最小生成树可能不唯一,但其对应的边的权值之和总是唯一的,并且是最小的。
- 最小生成树的边数为顶点数减 1 1 1。(树的性质)
注意:最小生成树中所有边的权值之和最小,不代表任意两个顶点之间的路径是最短路径。
构造最小生成树有多种算法,但大多数算法都利用了最小生成树的下列性质:假设 G = ( V , E ) G=(V,E) G=(V,E)是一个带权连通无向图, U U U是顶点集 V V V的一个非空子集。若 ( u , v ) (u,v) (u,v)是一条具有最小权值的边,其中 u ∈ U , v ∈ V − U u∈U, v∈V-U u∈U,v∈V−U,则必存在一棵包含边 ( u , v ) (u,v) (u,v)的最小生成树。
基于该性质的最小生成树算法主要有 P r i m Prim Prim算法和 K r u s k a l Kruskal Kruskal算法,它们都是基于贪心算法的策略,即通过多个局部最优解得到全局最优解。408初试中,需要掌握这两个算法的本质含义和基本思想,并能够手动模拟推演出其算法的实现步骤。
王道书上给出了一个通用的最小生成树算法的伪代码:
GENERIC_MST(G) {T=NULL;while T 未形成一棵生成树;do 找到一条最小代价边(u,v)并加入T后不会产生回路;T=T∪(u,v);
}
P r i m Prim Prim算法
P r i m Prim Prim(普里姆)算法的执行非常类似于寻找图的最短路径的 D i j k s t r a Dijkstra Dijkstra算法(下一节会讲)。
P r i m Prim Prim算法构造最小生成树的过程如下图 6.15 6.15 6.15所示(王道考研408数据结构2025 - P241)。初始时选取图中任一顶点(如顶点 1 1 1)加入树 T T T,此时树中只含有一个顶点,之后选择一个与当前 T T T中顶点集合距离最近的顶点,并将该顶点和相应的边加入 T T T,每次操作后 T T T中的顶点数和边数都增加 1 1 1。以此类推,直至图中所有的顶点都并入 T T T,得到的 T T T就是最小生成树。
(图片来自王道考研408数据结构2025)

P r i m Prim Prim算法的步骤如下:
- 假设 G = { V , E } G= \{V,E\} G={V,E}是连通图,其最小生成树 T = ( U , E T ) T=(U,E_T) T=(U,ET), E T E_T ET是最小生成树中边的集合。
- 初始化:向空树 T = ( U , E T ) T=(U,E_T) T=(U,ET)中添加图 G = ( V , E ) G=(V,E) G=(V,E)的任意一个顶点 u 0 u_0 u0,使 U = { u 0 } U=\{u_0\} U={u0}, E T = ∅ E_T=\emptyset ET=∅。
- 循环(重复下列操作直至 U = V U=V U=V):从图 G G G中选择满足 { ( u , v ) ∣ u ∈ U , v ∈ V − U } \left \{ \left ( u,v \right ) \mid u \in U, v \in V-U \right \} {(u,v)∣u∈U,v∈V−U}且具有最小权值的边 ( u , v ) (u,v) (u,v),加入树 T T T,置 U = U ∪ { v } U = U \cup \left \{ v \right \} U=U∪{v}, E T = E T ∪ { ( u , v ) } E_T = E_T \cup \left \{ \left ( u,v \right ) \right \} ET=ET∪{(u,v)}。
王道书上给出的 P r i m Prim Prim算法简单实现的伪代码如下,感兴趣的读者可以尝试完善之:
void Prim(G, T){T=∅; //初始化空树U={w}; //添加任意一个顶点wwhile((V-U)!=∅){ //若树中不含全部顶点设(u,v)是使u∈U与v∈(V−U),且权值最小的边T=T∪{(u,v)}; //边归入树U=U∪{v}; //顶点归入树}
}
P r i m Prim Prim算法的时间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2),不依赖于 ∣ E ∣ |E| ∣E∣,因此它适用于求解稠密图的最小生成树。虽然采用其他方法能改进 P r i m Prim Prim算法的时间复杂度,但增加了实现的复杂性。
相关例题:PTA 7-50 畅通工程之局部最小花费问题(传送门)
K r u s k a l Kruskal Kruskal算法
与 P r i m Prim Prim算法从顶点开始扩展最小生成树不同, K r u s k a l Kruskal Kruskal(克鲁斯卡尔)算法是一种按权值的递增次序选择合适的边来构造最小生成树的方法。
K r u s k a l Kruskal Kruskal算法构造最小生成树的过程如下图 6.16 6.16 6.16所示(王道考研408数据结构2025 - P241)。初始时为只有 n n n个顶点而无边的非连通图 T = { V , { } } T = \left \{ V,\left \{ \right \} \right \} T={V,{}},每个顶点自成一个连通分量。然后按照边的权值由小到大的排序,不断选取当前未被选取过且权值最小的边,若该边依附的顶点落在 T T T中不同的连通分量上(使用并查集判断这两个顶点是否属于同一棵集合树),则将此边加入 T T T,否则舍弃此边而选择下一条权值最小的边。以此类推,直至 T T T中所有顶点都在一个连通分量上。
(图片来自王道考研408数据结构2025)

知识点回顾:并查集
K r u s k a l Kruskal Kruskal算法的步骤如下:
- 假设 G = { V , E } G= \{V,E\} G={V,E}是连通图,其最小生成树 T = ( U , E T ) T=(U,E_T) T=(U,ET)。
- 初始化: U = V U=V U=V, E T = ∅ E_T=\emptyset ET=∅。即每个顶点构成的一棵独立的树, T T T此时是一个仅含 ∣ V ∣ |V| ∣V∣个顶点的森林。
- 循环(重复直至 T T T是一棵树):按 G G G的边的权值递增顺序依次从 E − E T E-E_T E−ET中选择一条边,若这条边加入 T T T后不构成回路,则将其加入 E T E_T ET,否则舍弃,直到 E T E_T ET中含有 n − 1 n-1 n−1条边。
王道书上给出的 K r u s k a l Kruskal Kruskal算法简单实现的伪代码如下,感兴趣的读者可以尝试完善之:
void Kruskal(V,T){T=V; //初始化树T,仅含顶点numS=n; //连通分量数while(numS>1){ //若连通分量数大于1从E中取出权值最小的边(v,u);if(v和u属于T中不同的连通分量){T=T∪{(v,u)}; //将此边加入生成树中numS--; //连通分量数减1}}
}
根据图的相关性质,若一条边连接了两棵不同树中的顶点,则对这两棵树来说,它必定是连通的,将这条边加入森林中,完成两棵树的合并,直到整个森林合并成一棵树。
在 K r u s k a l Kruskal Kruskal算法中,最坏情况下需要对 ∣ E ∣ |E| ∣E∣条边各扫描一次。通常采用堆(第 7 7 7章里会讲)来存放边的集合,每次选择最小权值的边需要 O ( l o g 2 ∣ E ∣ ) O(log_2|E|) O(log2∣E∣)的时间;每次使用并查集来快速判断两个顶点是否属于一个集合所需的时间为 O ( α ( ∣ V ∣ ) ) O(α(|V|)) O(α(∣V∣)), α ( ∣ V ∣ ) α(|V|) α(∣V∣)的增长极其缓慢,可视为常数。算法的总时间复杂度为 O ( ∣ E ∣ l o g 2 ∣ E ∣ ) O(|E|log_2|E|) O(∣E∣log2∣E∣),不依赖于 ∣ V ∣ |V| ∣V∣,因此 K r u s k a l Kruskal Kruskal算法适合顶点较多的稀疏图。
相关例题:洛谷P3366 【模板】最小生成树(传送门)
个人题解:【洛谷P3366】【模板】最小生成树 解题报告
对本小节内容,需要掌握手推Prim算法和Kruskal算法过程,能够模拟构建最小生成树,如有余力可以打一些代码题增强理解。
以上。
相关文章:

408数据结构-图的应用1-最小生成树 自学知识点整理
前置知识:图的遍历 图的应用是408初试历年考查的重点。不过一般而言,这部分内容直接以算法设计题形式考查的可能性极小,更多的是结合图的实例来考查算法的具体操作过程,要求掌握的是手推模拟给定图的各个算法执行过程。此外&#…...

Ubuntu18.04操作系统使用pip3安装open cv
在Ubuntu18.04操作系统环境下使用pip3安装opencv。安装方法如下: #pip3安装 sudo apt-get install python3-pip # 依赖包安装 sudo apt-get install libsm6 libxrender1 libxext6 #opencv安装;版本号自行填写 pip3 install opencv-python4.1.1.26 具体步骤 1、确认…...

为什么变量不可以在 switch 语句中声明定义?
目录 1.引言 2.switch语句的基本用法 3.为何不能在switch语句中声明变量 3.1.作用域问题 3.2.跳转语句的限制 4.解决方案 4.1.在switch语句之前声明变量 4.2.使用花括号创建新的作用域 5.总结 1.引言 在C/C等编程语言中,switch语句是一种常见的控制流结构&…...
手机定位技术全解析:原理、发展与应用
1. 引言 背景介绍 最近,神仙姐姐刘亦菲主演的电视剧《玫瑰的故事》中的一段情节引发了广泛讨论。剧中,方协文(丈夫)对玫瑰(妻子)的控制欲变本加厉,竟然偷偷在她的手机上安装监控软件ÿ…...

深入探索Kylin的Cube构建:数据魔方的构建之旅
深入探索Kylin的Cube构建:数据魔方的构建之旅 引言 Apache Kylin是一个开源的分布式分析引擎,提供Hadoop和Spark之上的高性能数据立方体(Cube)技术。Kylin的Cube构建过程是其核心功能之一,它允许用户定义和构建多维数…...
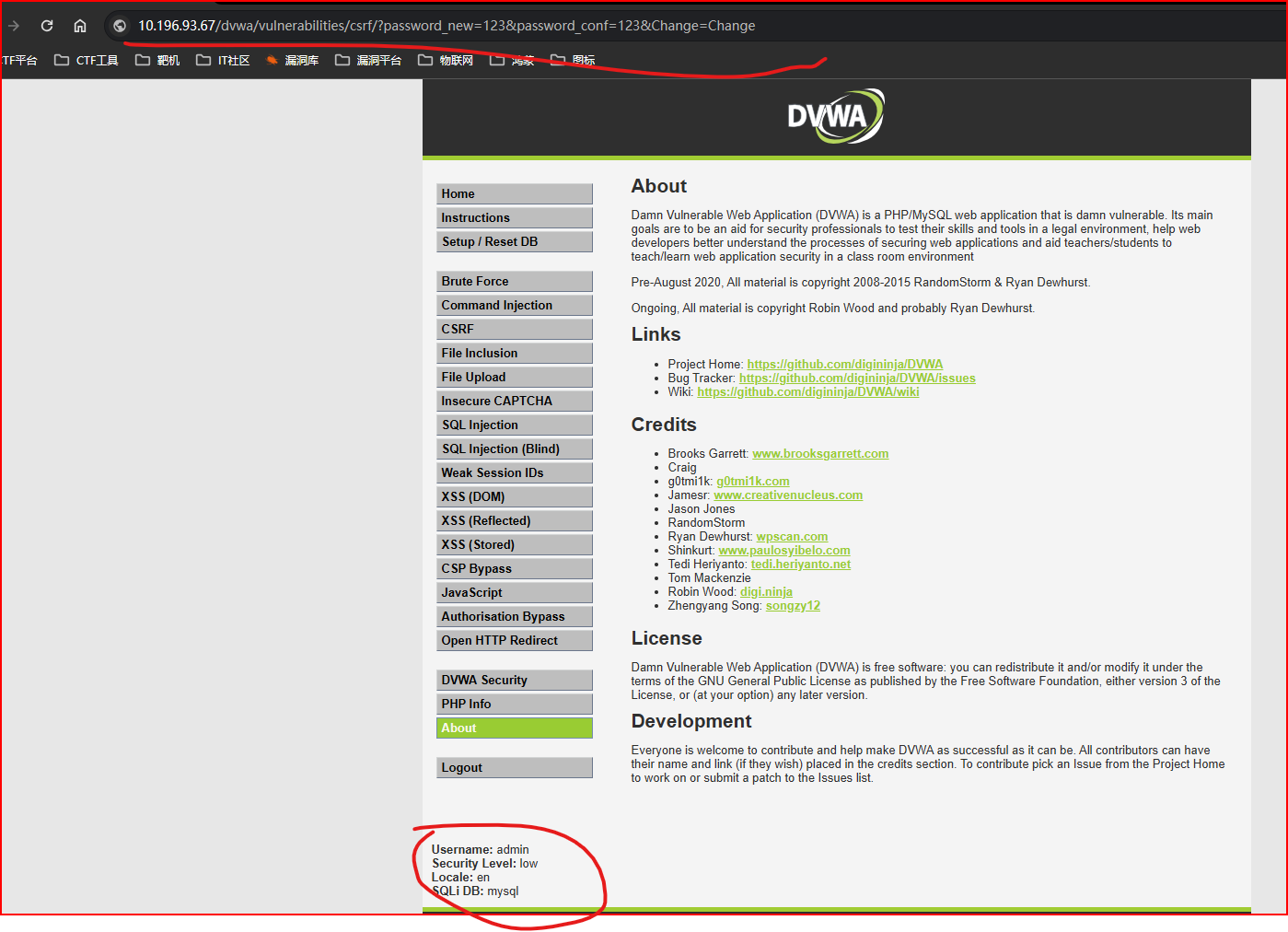
web渗透-CSRF漏洞
一、简介 cross-site request forgery 简称为"csrf",在csrf的攻击场景中攻击者会伪造一个请求(这个请求一般是一个链接),然后欺骗目标用户进行点击,用户一旦点击了这个请求,整个攻击就完成了。所以csrf攻击也为"o…...
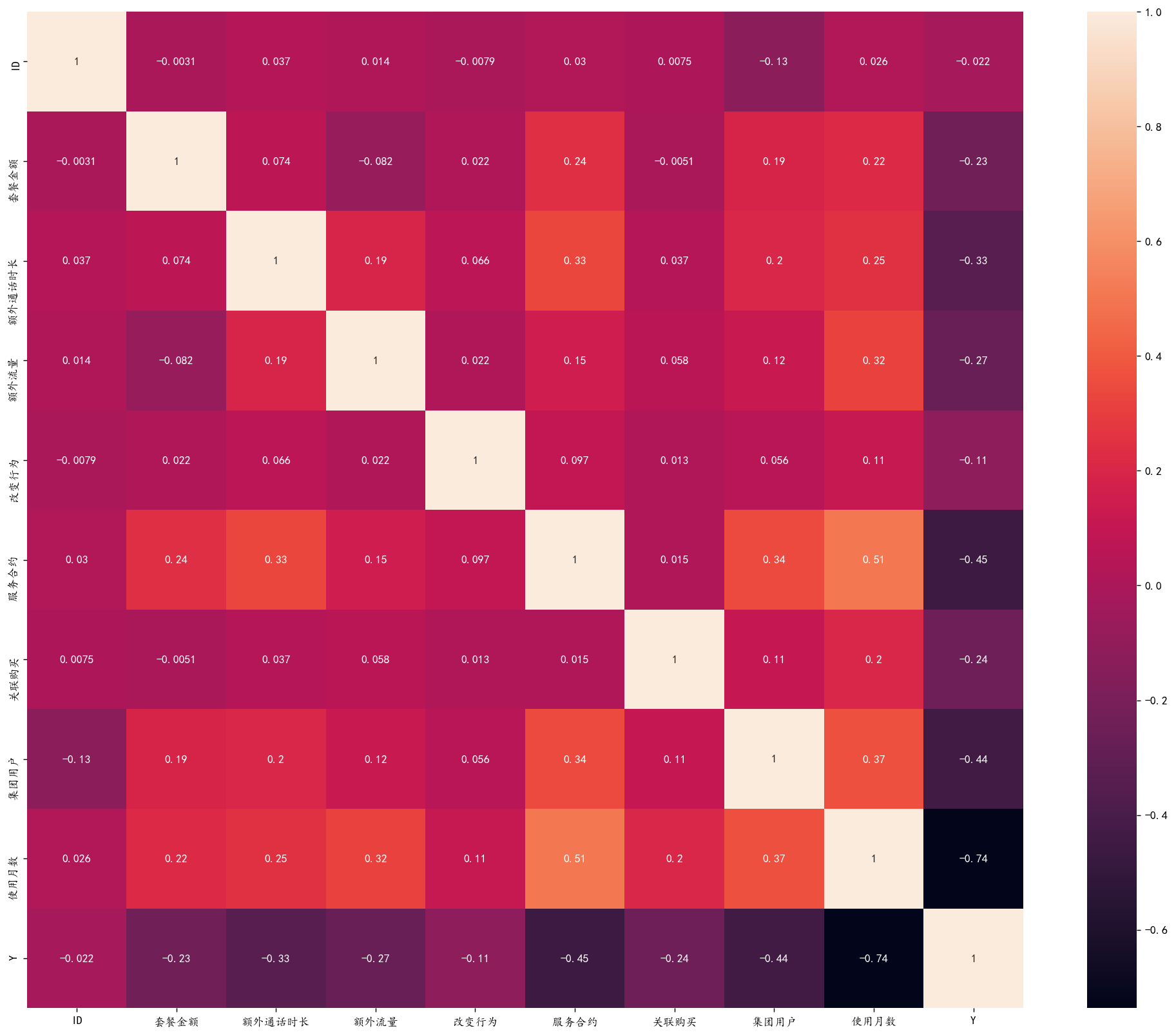
Python数据分析-电信客户流量预测与分析
一、背景介绍 研究背景:在快速发展和高度竞争的电信行业中,客户流失已成为运营商面临的主要挑战之一。电信服务的普及和用户选择的多样性使得保持客户忠诚度变得越来越困难。在这种背景下,准确预测客户流失并采取相应措施,对于运…...
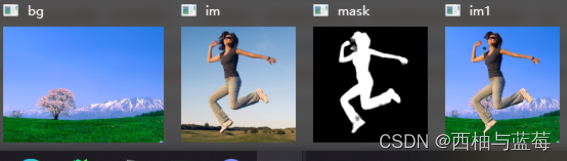
动态人物抠图换背景 MediaPipe
pip下载 MediaPipe pip install mediapipe -i 手部特征点模型包包含一个手掌检测模型和一个手部特征点检测模型。手掌检测模型在输入图片中定位手部,手部特征点检测模型可识别手掌检测模型定义的被剪裁手掌图片上的特定手部特征点。 由于运行手掌检测模型非常耗时&…...
)
Vue3 vite使用postcss-px-to-viewport(适配vant)
Vue3 vite使用postcss-px-to-viewport(适配vant) 安装vite.config.js配置 安装 npm install postcss-px-to-viewport-8-plugin -Dvite.config.js配置 import { fileURLToPath, URL } from node:urlimport { defineConfig } from vite import vue from …...

MCU复位时GPIO是什么状态?
大家一定遇到过上电或者复位时外部的MOS电路或者芯片使能信号意外开启,至此有经验的工程师就会经常关心一个问题,MCU复位时GPIO是什么状态?什么电路需要外部加上下拉? MCU从上电到启动,实际可分为复位前和复位后、初始…...
领先GPT-4o:Anthropic 推出新一代模型 Claude 3.5 Sonnet|TodayAI
Anthropic,全球领先的人工智能实验室之一,近日发布了其最新的人工智能模型——Claude 3.5 Sonnet。该模型不仅速度更快,成本更低,而且在多个关键任务上的表现超过了其前代模型 Claude 3 Opus。 更强的视觉功能与幽默感 Claude 3…...
使用AES,前端加密,后端解密,spring工具类了
学习python的时候,看到很多会对参数进行加密,于是好奇心驱使下,让我去了解了下AES加密如何在java中实现。 首先 npm install crypto-js 然后在你的方法中,给你们前端源码看看,因为我用的ruoyi框架做的实验ÿ…...

通过Spring-Data-Redis操作Redis
目录 一、搭建环境 (1)引入依赖 (2)自定义模板序列器 (3)编写配置文件 (4)操作方法 二、测试 一、搭建环境 (1)引入依赖 <dependencies><dep…...

自动驾驶ADAS
1 ToF摄像头分类 1.1 ToF原理 类似雷达测距,生成3D点云,或者叫3D贴图。ToF相机的分辨率一般在3万像素左右。ToF距离计算公式如图所示。 Figure 1-1 ToF距离计算公式 D:距离 c:光速 PHI:相位差 fmod:调制频率…...
Python+Pytest+Allure+Yaml接口自动化测试框架详解
PythonPytestAllureYaml接口自动化测试框架详解 编撰人:CesareCheung 更新时间:2024.06.20 一、技术栈 PythonPytestAllureYaml 版本要求:Python3.7.0,Pytest7.4.4,Allure2.18.1,PyYaml6.0 二、环境配置 1、安装python3.7,并配置…...
python turtle 001画两只小狗
效果图: 代码: pythonturtle001画两只小狗资源-CSDN文库 # 作者V w1933423import turtle # 导入turtle模块def draw_dogs():turtle.setup(800, 800) # 设置画布大小为800x800p turtle.Pen() # 创建一个画笔对象p.pensize(14) # 设置画笔大小为14p.…...
『亚马逊云科技产品测评』程序员最值得拥有的第一台专属服务器 “亚马逊EC2实例“
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 引言 自2006年8月9日,在搜索引擎大会(SES San Jo…...

python 趣味习题_递归函数(炸弹迷宫路径计算)
@[toc] python 学习中,常会遇到一些百思不得其解的难题,但有时“灵光一现”找准方法,难题便会迎刃而解。 本专栏旨在记录本人解决问题的思考方法,及实现过程。有更好方法或对程序执行有疑问的伙伴,可在评论区留言,共同讨论。 题目要求 题目描述:在一串连续的迷宫(房间…...

免费翻译API及使用指南——百度、腾讯
目录 一、百度翻译API 二、腾讯翻译API 一、百度翻译API 百度翻译API接口免费翻译额度:标准版(5万字符免费/每月)、高级版(100万字符免费/每月-需个人认证,基本都能通过)、尊享版(200万字符免…...
深度测试中的隐藏面消除技术
by STANCH 标签:#计算机图形学 #深度测试 #深度测试 #隐藏面消除 1.概述 根据我们的日常经验,近处的物体会挡住后面的物体,在三维场景中通常通过深度缓冲来实现这样的效果。深度缓冲记录着屏幕对应的每个像素的深度值。模型一开始所在的局部…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
