【贡献法】2262. 字符串的总引力
本文涉及知识点
贡献法
LeetCode2262. 字符串的总引力
字符串的 引力 定义为:字符串中 不同 字符的数量。
例如,“abbca” 的引力为 3 ,因为其中有 3 个不同字符 ‘a’、‘b’ 和 ‘c’ 。
给你一个字符串 s ,返回 其所有子字符串的总引力 。
子字符串 定义为:字符串中的一个连续字符序列。
示例 1:
输入:s = “abbca”
输出:28
解释:“abbca” 的子字符串有:
- 长度为 1 的子字符串:“a”、“b”、“b”、“c”、“a” 的引力分别为 1、1、1、1、1,总和为 5 。
- 长度为 2 的子字符串:“ab”、“bb”、“bc”、“ca” 的引力分别为 2、1、2、2 ,总和为 7 。
- 长度为 3 的子字符串:“abb”、“bbc”、“bca” 的引力分别为 2、2、3 ,总和为 7 。
- 长度为 4 的子字符串:“abbc”、“bbca” 的引力分别为 3、3 ,总和为 6 。
- 长度为 5 的子字符串:“abbca” 的引力为 3 ,总和为 3 。
引力总和为 5 + 7 + 7 + 6 + 3 = 28 。
示例 2:
输入:s = “code”
输出:20
解释:“code” 的子字符串有: - 长度为 1 的子字符串:“c”、“o”、“d”、“e” 的引力分别为 1、1、1、1 ,总和为 4 。
- 长度为 2 的子字符串:“co”、“od”、“de” 的引力分别为 2、2、2 ,总和为 6 。
- 长度为 3 的子字符串:“cod”、“ode” 的引力分别为 3、3 ,总和为 6 。
- 长度为 4 的子字符串:“code” 的引力为 4 ,总和为 4 。
引力总和为 4 + 6 + 6 + 4 = 20 。
提示:
1 <= s.length <= 105
s 由小写英文字母组成
贡献法
n = s.length
累计s[i]的对各子串贡献的引力。
s[left…r] 如果有相等的字符,则引力算到第一个字符上,下标最小字符。
令和s[i]相等的前一个下标为i1,则s[i]对符合以下条件的子数组贡献1:
[left,r] ,left ∈ \in ∈(i1,i] r ∈ \in ∈[i,n)
累计: (i-i1)*(n-i)
为了不处理边界情况v[0] =-1。
代码
核心代码
class Solution {
public:long long appealSum(string s) {vector<vector<int>> indexs(26, vector<int>(1, -1));const int N = s.length();for (int i = 0; i < N; i++) {indexs[s[i] - 'a'].emplace_back(i);}long long llRet = 0;for (const auto& v : indexs) {for (int i = 1; i < v.size(); i++) {llRet += (long long)(v[i] - v[i - 1]) * (N - v[i]);}}return llRet;}
};
单元测试
template<class T1, class T2>
void AssertEx(const T1& t1, const T2& t2)
{Assert::AreEqual(t1, t2);
}template<class T>
void AssertEx(const vector<T>& v1, const vector<T>& v2)
{Assert::AreEqual(v1.size(), v2.size());for (int i = 0; i < v1.size(); i++){Assert::AreEqual(v1[i], v2[i]);}
}template<class T>
void AssertV2(vector<vector<T>> vv1, vector<vector<T>> vv2)
{sort(vv1.begin(), vv1.end());sort(vv2.begin(), vv2.end());Assert::AreEqual(vv1.size(), vv2.size());for (int i = 0; i < vv1.size(); i++){AssertEx(vv1[i], vv2[i]);}
}namespace UnitTest
{ string s;TEST_CLASS(UnitTest){public:TEST_METHOD(TestMethod00){s = "c";auto res = Solution().appealSum(s);AssertEx(1LL, res);}TEST_METHOD(TestMethod03){s = "cc";auto res = Solution().appealSum(s);AssertEx(3LL, res);}TEST_METHOD(TestMethod01){s = "abbca";auto res = Solution().appealSum(s);AssertEx(28LL, res);}TEST_METHOD(TestMethod02){s = "code";auto res = Solution().appealSum(s);AssertEx(20LL, res);}};
}
扩展阅读
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关推荐
| 我想对大家说的话 |
|---|
| 《喜缺全书算法册》以原理、正确性证明、总结为主。 |
| 按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【贡献法】2262. 字符串的总引力
本文涉及知识点 贡献法 LeetCode2262. 字符串的总引力 字符串的 引力 定义为:字符串中 不同 字符的数量。 例如,“abbca” 的引力为 3 ,因为其中有 3 个不同字符 ‘a’、‘b’ 和 ‘c’ 。 给你一个字符串 s ,返回 其所有子字符…...
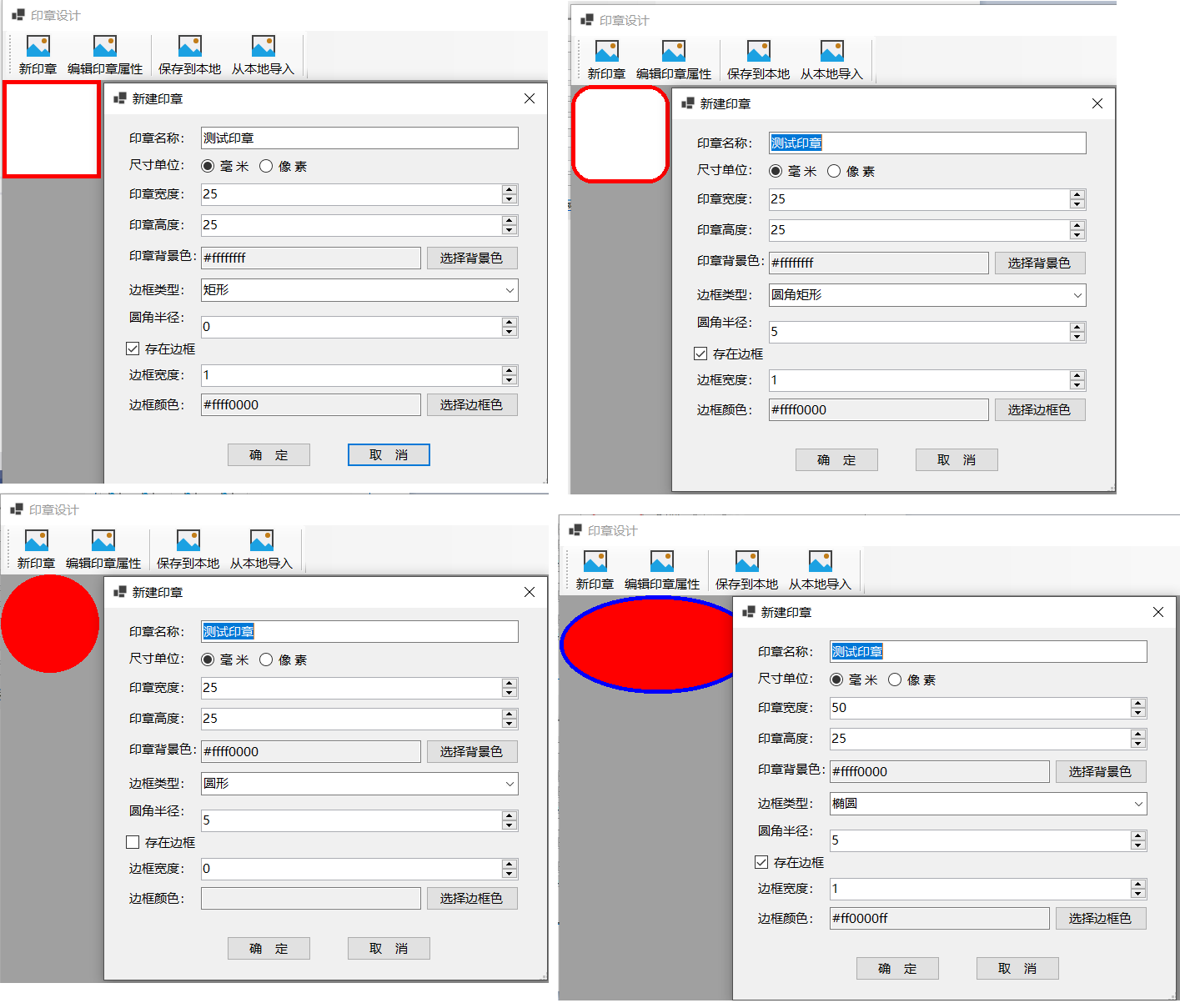
C#基于SkiaSharp实现印章管理(3)
本系列第一篇文章中创建的基本框架限定了印章形状为矩形,但常用的印章有方形、圆形等多种形状,本文调整程序以支持定义并显示矩形、圆角矩形、圆形、椭圆等4种形式的印章背景形状。 定义印章背景形状枚举类型,矩形、圆形、椭圆相关的尺寸…...

如何理解泛型的编译期检查
既然说类型变量会在编译的时候擦除掉,那为什么我们往 ArrayList 创建的对象中添加整数会报错呢?不是说泛型变量String会在编译的时候变为Object类型吗?为什么不能存别的类型呢?既然类型擦除了,如何保证我们只能使用泛型…...
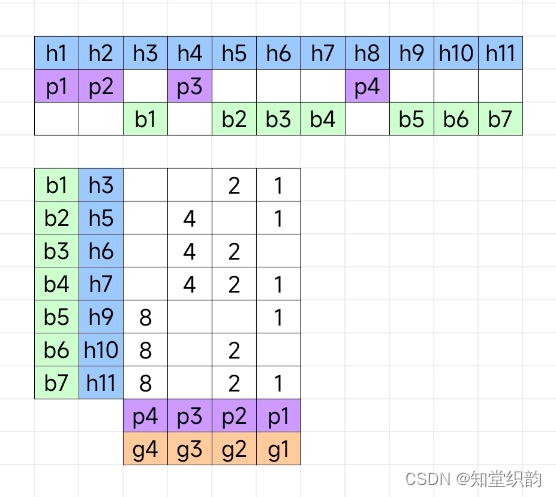
计算机组成原理:海明校验
在上图中,对绿色的7比特数据进行海明校验,需要添加紫色的4比特校验位,总共是蓝色的11比特。紫色的校验位pi分布于蓝色的hi的1, 2, 4, 8, 16, 32, 64位,是2i-1位。绿色的数据位bi分布于剩下的位。 在下图中,b1位于h3&a…...
信息学奥赛初赛天天练-39-CSP-J2021基础题-哈夫曼树、哈夫曼编码、贪心算法、满二叉树、完全二叉树、前中后缀表达式转换
PDF文档公众号回复关键字:20240629 2022 CSP-J 选择题 单项选择题(共15题,每题2分,共计30分:每题有且仅有一个正确选项) 5.对于入栈顺序为a,b,c,d,e的序列,下列( )不合法的出栈序列 A. a,b&a…...

第11章 规划过程组(收集需求)
第11章 规划过程组(一)11.3收集需求,在第三版教材第377~378页; 文字图片音频方式 第一个知识点:主要输出 1、需求跟踪矩阵 内容 业务需要、机会、目的和目标 项目目标 项目范围和 WBS 可…...

探索WebKit的守护神:深入Web安全策略
探索WebKit的守护神:深入Web安全策略 在数字化时代,网络已成为我们生活的一部分,而网页浏览器作为我们探索网络世界的窗口,其安全性至关重要。WebKit作为众多流行浏览器的内核,例如Safari,其安全性策略是保…...

unity ScrollRect裁剪ParticleSystem粒子
搜了下大概有这几种方法 通过模板缓存通过shader裁剪区域:案例一,案例二,案例三,三个案例都是类似的方法,需要在c#传入数据到shader通过插件 某乎上的模板缓存方法link,(没有登录看不到全文&a…...

凤仪亭 | 第7集 | 大丈夫生居天地之间,岂能郁郁久居人下 | 司徒一言,令我拨云见日,茅塞顿开 | 三国演义 | 逐鹿群雄
🙋大家好!我是毛毛张! 🌈个人首页: 神马都会亿点点的毛毛张 📌这篇博客分享的是《三国演义》文学剧本第Ⅰ部分《群雄逐鹿》的第7️⃣集《凤仪亭》的经典语句和文学剧本全集台词 文章目录 1.经典语句2.文学剧本台词 …...

React实战学习(一)_棋盘设计
需求: 左上侧:状态左下侧:棋盘,保证胜利就结束 和 下过来的不能在下右侧:“时光机”,保证可以回顾,索引 语法: 父子之间属性传递(props)子父组件传递(写法上&…...

【LeetCode】每日一题:三数之和
解题思路 最开始是打算沿着二数之和的思路做,即固定了最大的,然后小的开始遍历,因为这种遍历方式只需要遍历一轮就能完成,所以复杂度应该是O(n2),但是最后几个示例还是超时了,可能进…...

逆风而行:提升逆商,让困难成为你前进的动力
一、引言 生活,总是充满了未知与变数。有时,我们会遇到阳光明媚的日子,享受着宁静与和谐;但更多时候,我们却不得不面对那些突如其来的坏事件,如工作的挫折、人际关系的困扰、健康的挑战等。这些事件如同突…...

新能源汽车CAN总线故障定位与干扰排除的几个方法
CAN总线是目前最受欢迎的现场总线之一,在新能源车中有广泛应用。新能源车的CAN总线故障和隐患将影响驾驶体验甚至行车安全,如何进行CAN总线故障定位及干扰排除呢? 目前,国内机动车保有量已经突破三亿大关。由于大量的燃油车带来严峻的环境问题,因此全面禁售燃油车的日程在…...
【涵子来信】——社交宝典:克服你心中的内向,世界总有缺陷
内向,你是内向的吗?想必每个人不同,面对的情形也是不同的。 暑假是一个很好的机会,我是可以去多社交社交。但是,面对着CSDN上这么多技术人er,那么,我的宝典,对于大家,有…...

LabVIEW项目外协时选择公司与个人兼职的比较
在选择LabVIEW项目外协合作伙伴时,外协公司和个人兼职各有优劣。个人兼职成本较低且灵活,但在可靠性、技术覆盖面、资源和风险管理上存在不足。而外协公司拥有专业团队、丰富资源、完善的项目管理和风险控制,尽管成本较高,但能提…...

汽车电子工程师入门系列——CAN 规范系列通读
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

泽众云真机-平台华为机型HarmonyOS NEXT系统已上线!
泽众云真机平台华为机型HarmonyOS NEXT系统已上线! 之前文章《泽众云真机-平台即将升级支持华为机型HarmonyOS NEXT系统泽众云真机-平台即将升级支持华为机型HarmonyOS NEXT系统》,为什么要升级HarmonyOS NEXT系统?我们之前有说过,…...

AI基础:从线性回归到梯度下降
一个简单的问题: 如果此时你正站在迷路缭绕的山坡上,能见度不高,但是你又想去往最低的山谷的位置,怎么走? 很简单,哪里陡那就往那里走呗——而这就是梯度下降算法的思想。 古话说:“先发制于人…...

AI产品经理面试
把优秀当习惯把优秀当习惯肯定不是口头说说,那有什么判断标准吗? 当我做完一件事儿的时候,我会看它有没有突破我的舒适圈、能不能惊艳到我自己。这就是我的判断标准。 在自我介绍和经历介绍时,面试者应该注重以下几个方面…...

二进制方式部署consul单机版
1.consul的下载 mkdir -p /root/consul/data && cd /root/consul wget https://releases.hashicorp.com/consul/1.18.0/consul_1.18.0_linux_amd64.zip unzip consul_1.18.0_linux_amd64.zip mv consul /usr/local/bin/ 2.配置文件 // 配置文件路径: /roo…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
