K 近邻、K-NN 算法图文详解
1. 为什么学习KNN算法
KNN是监督学习分类算法,主要解决现实生活中分类问题。根据目标的不同将监督学习任务分为了分类学习及回归预测问题。
KNN(K-Nearest Neihbor,KNN)K近邻是机器学习算法中理论最简单,最好理解的算法,是一个非常适合入门的算法,拥有如下特性:
- 思想极度简单,应用数学知识少(近乎为零),对于很多不擅长数学的小伙伴十分友好
- 虽然算法简单,但效果也不错
2. KNN 原理

上图中每一个数据点代表一个肿瘤病历:
- 横轴表示肿瘤大小,纵轴表示发现时间
- 恶性肿瘤用蓝色表示,良性肿瘤用红色表示
疑问:新来了一个病人(下图绿色的点),如何判断新来的病人(即绿色点)是良性肿瘤还是恶性肿瘤?
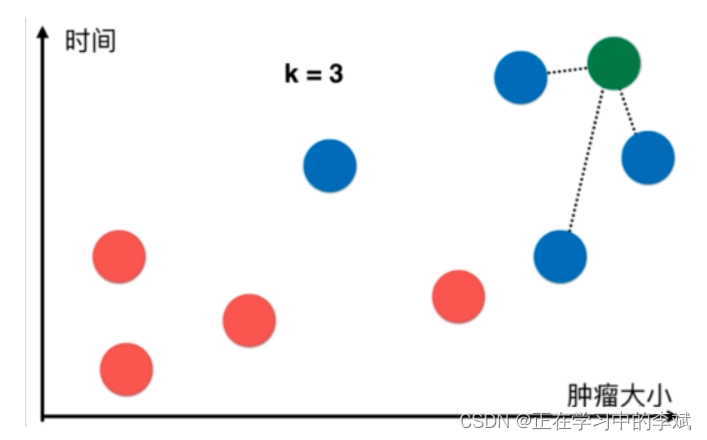
解决方法:k-近邻算法的做法如下:
(1)取一个值k=3(k值后面介绍,现在可以理解为算法的使用者根据经验取的最优值)
(2)在所有的点中找到距离绿色点最近的三个点
(3)让最近的点所属的类别进行投票
(4)最近的三个点都是蓝色的,所以该病人对应的应该也是蓝色,即恶性肿瘤。
3. 距离度量方法
机器学习算法中,经常需要 判断两个样本之间是否相似 ,比如KNN,K-means,推荐算法中的协同过滤等等,常用的套路是 将相似的判断转换成距离的计算 ,距离近的样本相似程度高,距离远的相似程度低。所以度量距离是很多算法中的关键步骤。
KNN算法中要求数据的所有特征都用数值表示。若在数据特征中存在非数值类型,必须采用手段将其进行量化为数值。
- 比如样本特征中包含有颜色(红、绿、蓝)一项,颜色之间没有距离可言,可通过将颜色转化为 灰度值来实现距离计算 。
- 每个特征都用数值表示,样本之间就可以计算出彼此的距离来
3.1 欧式距离

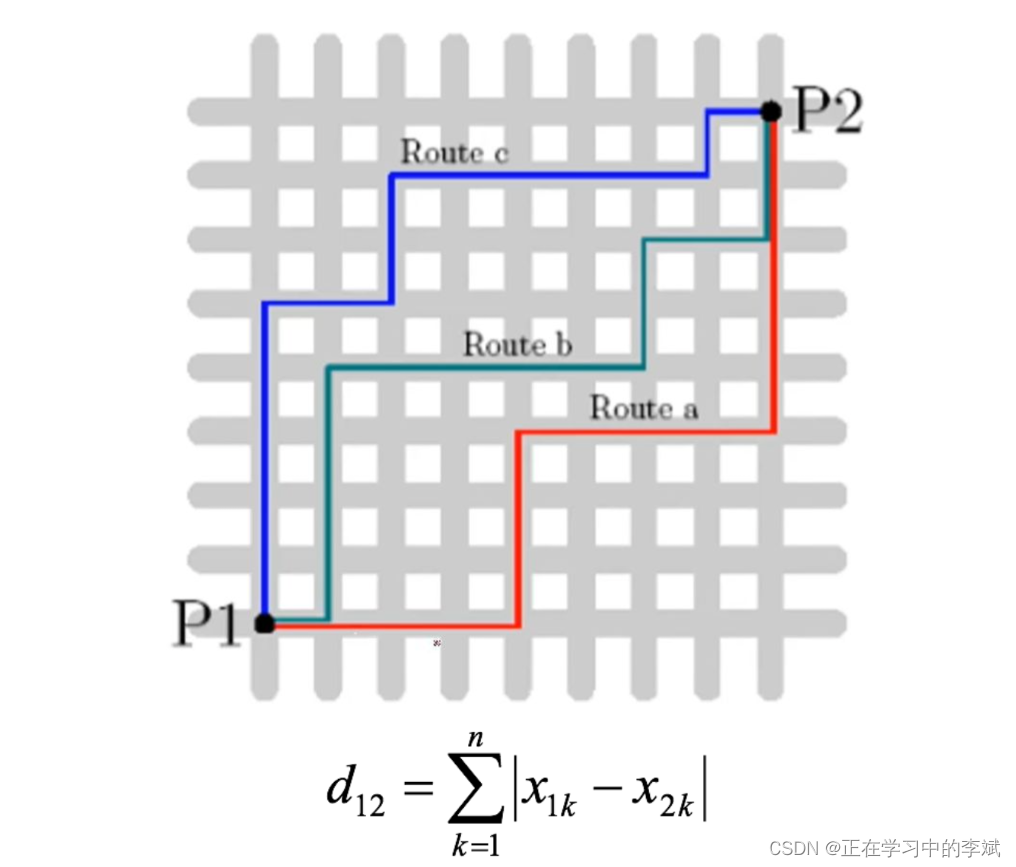
3.2 曼哈顿距离
3.3 切比雪夫距离(了解)
3.4 闵式距离
闵氏距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述。

其中p是一个变参数:
- 当 p=1 时,就是曼哈顿距离;
- 当 p=2 时,就是欧氏距离;
- 当 p→∞ 时,就是切比雪夫距离。
根据 p 的不同,闵氏距离可以表示某一类/种的距离。
4. 归一化和标准化
样本中有多个特征,每一个特征都有自己的定义域和取值范围,他们对距离计算也是不同的,如取值较大的影响力会盖过取值较小的参数。因此,为了公平,样本参数必须做一些归一化处理,将不同的特征都缩放到相同的区间或者分布内。

4.1 归一化
from sklearn.preprocessing import MinMaxScaler# 1. 准备数据
data = [[90, 2, 10, 40],[60, 4, 15, 45],[75, 3, 13, 46]]
# 2. 初始化归一化对象
transformer = MinMaxScaler()
# 3. 对原始特征进行变换
data = transformer.fit_transform(data)
# 4. 打印归一化后的结果
print(data)
归一化受到最大值与最小值的影响,这种方法容易受到异常数据的影响, 鲁棒性较差,适合传统精确小数据场景
4.2 标准化
from sklearn.preprocessing import StandardScaler# 1. 准备数据
data = [[90, 2, 10, 40],[60, 4, 15, 45],[75, 3, 13, 46]]
# 2. 初始化标准化对象
transformer = StandardScaler()
# 3. 对原始特征进行变换
data = transformer.fit_transform(data)
# 4. 打印归一化后的结果
print(data)
对于标准化来说,如果出现异常点,由于具有一定数据量,少量的异常点对于平均值的影响并不大
5. K 值选择问题
KNN算法的关键是什么?
答案一定是K值的选择,下图中K=3,属于红色三角形,K=5属于蓝色的正方形。这个时候就是K选择困难的时候。

使用 scikit-learn 提供的 GridSearchCV 工具, 配合交叉验证法可以搜索参数组合.
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV# 1. 加载数据集
x, y = load_iris(return_X_y=True)# 2. 分割数据集
x_train, x_test, y_train, y_test = \train_test_split(x, y, test_size=0.2, stratify=y, random_state=0)# 3. 创建网格搜索对象
estimator = KNeighborsClassifier()
param_grid = {'n_neighbors': [1, 3, 5, 7]}
estimator = GridSearchCV(estimator, param_grid=param_grid, cv=5, verbose=0)
estimator.fit(x_train, y_train)# 4. 打印最优参数
print('最优参数组合:', estimator.best_params_, '最好得分:', estimator.best_score_)# 4. 测试集评估模型
print('测试集准确率:', estimator.score(x_test, y_test))
6. 数据集划分
为了能够评估模型的泛化能力,可以通过实验测试对学习器的泛化能力进行评估,进而做出选择。因此需要使用一个 “测试集” 来测试学习器对新样本的判别能力,以测试集上的 “测试误差” 作为泛化误差的近似。
6.1 留出法(简单交叉验证)
留出法 (hold-out) 将数据集 D 划分为两个互斥的集合,其中一个集合作为训练集 S,另一个作为测试集 T。
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import ShuffleSplit
from collections import Counter
from sklearn.datasets import load_irisdef test01():# 1. 加载数据集x, y = load_iris(return_X_y=True)print('原始类别比例:', Counter(y))# 2. 留出法(随机分割)x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)print('随机类别分割:', Counter(y_train), Counter(y_test))# 3. 留出法(分层分割)x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, stratify=y)print('分层类别分割:', Counter(y_train), Counter(y_test))def test02():# 1. 加载数据集x, y = load_iris(return_X_y=True)print('原始类别比例:', Counter(y))print('*' * 40)# 2. 多次划分(随机分割)spliter = ShuffleSplit(n_splits=5, test_size=0.2, random_state=0)for train, test in spliter.split(x, y):print('随机多次分割:', Counter(y[test]))print('*' * 40)# 3. 多次划分(分层分割)spliter = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=0)for train, test in spliter.split(x, y):print('分层多次分割:', Counter(y[test]))if __name__ == '__main__':test01()test02()
6.2 交叉验证法
K-Fold交叉验证,将数据随机且均匀地分成k分,每次使用k-1份数据作为训练,而使用剩下的一份数据进行测试
from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold
from collections import Counter
from sklearn.datasets import load_irisdef test():# 1. 加载数据集x, y = load_iris(return_X_y=True)print('原始类别比例:', Counter(y))print('*' * 40)# 2. 随机交叉验证spliter = KFold(n_splits=5, shuffle=True, random_state=0)for train, test in spliter.split(x, y):print('随机交叉验证:', Counter(y[test]))print('*' * 40)# 3. 分层交叉验证spliter = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)for train, test in spliter.split(x, y):print('分层交叉验证:', Counter(y[test]))if __name__ == '__main__':test()
6.3 留一法
留一法( Leave-One-Out,简称LOO),即每次抽取一个样本做为测试集。
from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import LeavePOut
from sklearn.datasets import load_iris
from collections import Counterdef test01():# 1. 加载数据集x, y = load_iris(return_X_y=True)print('原始类别比例:', Counter(y))print('*' * 40)# 2. 留一法spliter = LeaveOneOut()for train, test in spliter.split(x, y):print('训练集:', len(train), '测试集:', len(test), test)print('*' * 40)# 3. 留P法spliter = LeavePOut(p=3)for train, test in spliter.split(x, y):print('训练集:', len(train), '测试集:', len(test), test)if __name__ == '__main__':test01()
6.4 自助法
每次随机从D中抽出一个样本,将其拷贝放入D,然后再将该样本放回初始数据集D中,使得该样本在下次采样时仍有可能被抽到;
这个过程重复执行m次后,我们就得到了包含m个样本的数据集D′,这就是自助采样的结果。
import pandas as pdif __name__ == '__main__':# 1. 构造数据集data = [[90, 2, 10, 40],[60, 4, 15, 45],[75, 3, 13, 46],[78, 2, 64, 22]]data = pd.DataFrame(data)print('数据集:\n',data)print('*' * 30)# 2. 产生训练集train = data.sample(frac=1, replace=True)print('训练集:\n', train)print('*' * 30)# 3. 产生测试集test = data.loc[data.index.difference(train.index)]print('测试集:\n', test)
7. 可执行示例代码
以下是 K-NN 算法的实现示例代码,使用 scikit-learn 库:
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score# 示例数据
X = np.array([[1, 2], [2, 3], [3, 4], [6, 7], [7, 8], [8, 9]])
y = np.array([0, 0, 0, 1, 1, 1])# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)# 创建KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)# 训练模型(实际上只是存储数据)
knn.fit(X_train, y_train)# 进行预测
y_pred = knn.predict(X_test)# 计算准确率,分类算法的评估
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
通过这个示例,可以看到 K-NN 算法的基本流程和实现。该算法通过计算距离来进行分类,并可以通过调整 K 值来优化模型性能。
8. K-NN 算法总结
K-NN(K-Nearest Neighbors)算法是一种基于实例的学习方法,用于分类和回归。它通过计算样本与训练集中所有样本之间的距离,选择最近的 K 个邻居,然后根据这些邻居的标签进行预测。
特点
- 基于实例:没有显式的训练过程,直接使用训练数据进行预测。
- 懒惰学习:训练阶段只是存储数据,实际的计算发生在预测阶段。
- 非参数化:不对数据进行任何假设。
优点
- 简单易实现:实现起来相对简单,理解容易。
- 无需假设数据分布:对数据的分布没有任何假设。
- 适用于分类和回归:可以同时用于分类和回归问题。
- 灵活性:可以处理多类别分类问题。
缺点
- 计算复杂度高:预测时需要计算新样本与所有训练样本的距离,计算量大,尤其是数据量大时。
- 存储复杂度高:需要存储所有的训练数据。
- 对噪音敏感:容易受到噪音和异常值的影响。
- 维度灾难:高维数据时,计算距离的效果会变差,需要进行降维处理。
关键
- 选择合适的 K 值:K 值过小容易过拟合,K 值过大容易欠拟合。通常通过交叉验证选择合适的 K 值。
- 距离度量:常用的距离度量方法有欧氏距离、曼哈顿距离、闵可夫斯基距离等。
- 特征缩放:在计算距离前,需要对特征进行标准化或归一化处理,以避免特征值范围差异导致的计算偏差。
过程
- 数据准备:准备训练数据集和测试数据集。
- 计算距离:对于每个测试样本,计算它与所有训练样本之间的距离。
- 选择邻居:选择距离最近的 K 个邻居。
- 投票或平均:
- 分类:对 K 个邻居的类别进行投票,选择出现次数最多的类别作为预测结果。
- 回归:对 K 个邻居的目标值进行平均,作为预测结果。
- 输出结果:输出测试样本的预测结果。
相关文章:

K 近邻、K-NN 算法图文详解
1. 为什么学习KNN算法 KNN是监督学习分类算法,主要解决现实生活中分类问题。根据目标的不同将监督学习任务分为了分类学习及回归预测问题。 KNN(K-Nearest Neihbor,KNN)K近邻是机器学习算法中理论最简单,最好理解的算法…...

Eclipse + GDB + J-Link 的单片机程序调试实践
Eclipse GDB J-Link 的调试实践 本文介绍如何创建Eclipse的调试配置,如何控制调试过程,如何查看修改各种变量。 对 Eclipse 的要求 所用 Eclipse 应当安装了 Eclipse Embedded CDT 插件。从 https://www.eclipse.org/downloads/packages/ 下载 Ecli…...

前端代码生成辅助工具
1,Axure Axure设计的界面如何生成HTML文件 https://blog.csdn.net/qq_43279782/article/details/112387511 Axure 生成HTML 文件,并用Chrome打开 https://blog.csdn.net/qq_30718137/article/details/80621025 2,OpenUI [开源] OpenUI …...

静态库与动态库总结
一、库文件和头文件 所谓库文件,可以将其理解为压缩包文件,该文件内部通常包含不止一个目标文件(也就是二进制文件)。 值得一提的是,库文件中每个目标文件存储的代码,并非完整的程序,而是一个…...

深入解析tcpdump:网络数据包捕获与分析的利器
引言 在网络技术日新月异的今天,网络数据包的捕获与分析成为了网络管理员、安全专家以及开发人员不可或缺的技能。其中,tcpdump作为一款强大的网络数据包捕获分析工具,广泛应用于Linux系统中。本文将从技术人的角度,详细分析tcpdu…...

【漏洞复现】科立讯通信有限公司指挥调度管理平台uploadgps.php存在SQL注入
0x01 产品简介 科立讯通信指挥调度管理平台是一个专门针对通信行业的管理平台。该产品旨在提供高效的指挥调度和管理解决方案,以帮助通信运营商或相关机构实现更好的运营效率和服务质量。该平台提供强大的指挥调度功能,可以实时监控和管理通信网络设备、…...
什么是自然语言处理(NLP)?详细解读文本分类、情感分析和机器翻译的核心技术
什么是自然语言处理? 自然语言处理(Natural Language Processing,简称NLP)是人工智能的一个重要分支,旨在让计算机理解、解释和生成人类的自然语言。打个比方,你和Siri对话,或使用谷歌翻译翻译一…...

【linux】gcc快速入门教程
目录 一.gcc简介 二.gcc常用命令 一.gcc简介 gcc 是GNU Compiler Collection(GNU编译器套件)。就是一个编译器。编译一个源文件的时候可以直接使用,但是源文件数量太多时,就很不方便,于是就出现了make 工具 二.gcc…...
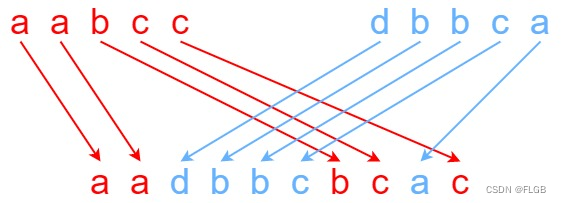
【多维动态规划】Leetcode 97. 交错字符串【中等】
交错字符串 给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。 两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串 子字符串 是字符串中连续的 非空 字符序列。 s s1 s2 … snt…...

【JavaScript脚本宇宙】精通前端开发:六大热门CSS框架详解
前端开发的利器:深入了解六大CSS框架 前言 在现代Web开发中,选择适合的前端框架和工具包是构建高效、响应式和美观的网站或应用程序的关键。本文将详细介绍六个广受欢迎的CSS框架:Bootstrap、Bulma、Tailwind CSS、Foundation、Materialize…...

开发技术-Java集合(List)删除元素的几种方式
文章目录 1. 错误的删除2. 正确的方法2.1 倒叙删除2.2 迭代器删除2.3 removeAll() 删除2.4 removeIf() 最简单的删除 3. 总结 1. 错误的删除 在写代码时,想将其中的一个元素删除,就遍历了 list ,使用了 remove(),发现效果并不是想…...

c++ 递归
递归函数是指在函数定义中调用自身的函数。C语言也支持递归函数。 下面是一个使用递归函数计算阶乘的例子: #include <iostream> using namespace std;int factorial(int n) {// 基本情况,当 n 等于 0 或 1 时,阶乘为 1if (n 0 || n…...
RedHat9 | podman容器
1、容器技术介绍 传统问题 应用程序和依赖需要一起安装在物理主机或虚拟机上的操作系统应用程序版本比当前操作系统安装的版本更低或更新两个应用程序可能需要某一软件的不同版本,彼此版本之间不兼容 解决方式 将应用程序打包并部署为容器容器是与系统的其他部分…...

边缘计算项目有哪些
边缘计算项目在多个领域得到了广泛的应用,以下是一些典型的边缘计算项目案例: 1. **智能交通系统**:通过在交通信号灯、监控摄像头等设备上部署边缘计算,可以实时分析交通流量,优化交通信号控制,减少拥堵&…...

计算fibonacci数列每一项时所需的递归调用次数
斐波那契数列是一个经典的数列,其中每一项是前两项的和,定义为: [ F(n) F(n-1) F(n-2) ] 其中,( F(0) 0 ) 和 ( F(1) 1 )。 对于计算斐波那契数列的第 ( n ) 项,如果使用简单的递归方法,其时间复杂度是…...

【教学类65-05】20240627秘密花园涂色书(中四班练习)
【教学类65-03】20240622秘密花园涂色书03(通义万相)(A4横版1张,一大 68张纸136份)-CSDN博客 背景需求: 打印以下几款秘密花园样式(每款10份)给中四班孩子玩一下,看看效果 【教学类…...
)
Python 学习之基础语法(一)
Python的语法基础主要包括以下几个方面,下面将逐一进行分点表示和归纳: 一、基本语法 1. 注释 a. 单行注释:使用#开头,例如# 这是一个单行注释。 b. 多行注释:使用三引号(可以是三个单引号或三个双引号&…...
日志分析-windows系统日志分析
日志分析-windows系统日志分析 使用事件查看器分析Windows系统日志 cmd命令 eventvwr 筛选 清除日志、注销并重新登陆,查看日志情况 Windows7和Windowserver2008R2的主机日志保存在C:\Windows\System32\winevt\Logs文件夹下,Security.evtx即为W…...

【ARM】MDK工程切换高版本的编译器后出现error A1137E报错
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 解决工程从Compiler 5切换到Compiler 6进行编译时出现一些非语法问题上的报错。 2、 问题场景 对于一些使用Compiler 5进行编译的工程,要切换到Compiler 6进行编译的时候,原本无任何报错警告…...

深入 SSH:解锁本地转发、远程转发和动态转发的潜力
文章目录 前言一、解锁内部服务:SSH 本地转发1.1 什么是 SSH 本地转发1.2 本地转发应用场景 二、打开外部访问大门:SSH 远程转发2.1 什么是 SSH 远程转发2.2 远程转发应用场景 三、动态转发:SSH 让你拥有自己的 VPN3.1 什么是 SSH 动态转发3.…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
