Python和MATLAB粘性力接触力动态模型半隐式欧拉算法
🎯要点
🎯运动力模型计算制作过程:🖊相机捕捉网球运动图,制定运动数学模型,数值微分运动方程 | 🖊计算运动,欧拉算法离散积分运动,欧拉-克罗默算法微分运动方程
🎯粘性力模型计算制作过程:🖊绘制雨滴、环境和坐标系下落自由体草图,使用牛顿第二定律制定运动数学模型,定义无空气阻力和恒速简化数学模型,数值模型解析
🎯固体-固体接触力模型计算制作过程:🖊实验绘制悬块弹簧形变量图,使用牛顿第二定律制定平衡模型,定义无空气阻力简化数学模型,欧拉-克罗默算法数值求解,制作三维动态可视图
🎯移动物体间复合力模型计算制作过程:🖊实验绘制电梯,物重和人自由体图,模型使用牛顿第三定律确定力对和牛顿第二定律确定图中运动体,解析无运动和相对运动简化力模型
🎯龙卷风、弹跳球和河流上船只三维运动力模型计算制作过程 | 🎯加速实验车、旋转杆、圆周运动,风中的珠子和地震期间的振荡中约束运动力模型计算制作过程
📜物理学和数学模型用例 | 本文
📜物理数学波形方程:Python数值和符号算法计算及3D视图物理数学波形方程
📜物理数学热力学静电学和波动方程:Python和C++数学物理计算分形热力学静电学和波动方程
📜物理数学拉格朗日和哈密顿动力学:Python计算物理粒子及拉格朗日和哈密顿动力学
📜物理数学气体动能和粒子速度:MATLAB和Python数值和符号计算可视化物理学气体动能和粒子速度
📜物理统计推理模型:Python射频电磁肿瘤热疗数学模型和电磁爆炸性变化统计推理模型
📜物理数学流体力学:C++风流和MATLAB | Python | CUDA 库埃特流泊肃叶流薄膜流体
📜物理数学气体运动模型:C++ | Python气泡表面张力和预期形态及上升速度数值模型


🍇Python半隐式欧拉方法
在数学中,半隐式欧拉方法也称为辛欧拉、半显式欧拉、欧拉-克罗默和牛顿-斯托默-韦莱,是欧拉方法的一种改进,用于求解哈密顿方程,哈密顿方程是经典力学中出现的常微分方程组。半隐式欧拉方法是一种辛积分器,因此比标准欧拉方法能得到更好的结果。
半隐式欧拉方法可以应用于一对以下形式的微分方程:
d x d t = f ( t , v ) d v d t = g ( t , x ) \begin{aligned} & \frac{d x}{d t}=f(t, v) \\ & \frac{d v}{d t}=g(t, x) \end{aligned} dtdx=f(t,v)dtdv=g(t,x)
其中 f f f 和 g g g 是给定函数。这里, x x x和 v v v可以是标量或向量。如果哈密顿量具有以下形式,则哈密顿力学中的运动方程采用这种形式
H = T ( t , v ) + V ( t , x ) H=T(t, v)+V(t, x) H=T(t,v)+V(t,x)
微分方程需在初始条件下求解
x ( t 0 ) = x 0 , v ( t 0 ) = v 0 x\left(t_0\right)=x_0, \quad v\left(t_0\right)=v_0 x(t0)=x0,v(t0)=v0
欧拉方法对于振荡系统存在一个根本问题。再看一下欧拉方法的近似,得到下一个时间间隔的位置:
x ( t i + Δ t ) ≈ x ( t i ) + v ( t i ) Δ t x\left(t_i+\Delta t\right) \approx x\left(t_i\right)+v\left(t_i\right) \Delta t x(ti+Δt)≈x(ti)+v(ti)Δt
它使用时间间隔开始时的速度值来将解逐步推向未来。
由于欧拉方法通过线性近似将解投影到未来,并假设区间开始时的导数值,因此它对于振荡函数来说不是很好。改进欧拉方法的一个聪明的想法是使用第二个方程的导数的更新值。
纯欧拉方法适用:
x ( t 0 ) = x 0 , x i + 1 = x i + v i Δ t v ( t 0 ) = v 0 , v i + 1 = v i − ω 2 x i Δ t \begin{aligned} x\left(t_0\right)=x_0, & x_{i+1}=x_i+v_i \Delta t \\ v\left(t_0\right)=v_0, & v_{i+1}=v_i-\omega^2 x_i \Delta t \end{aligned} x(t0)=x0,v(t0)=v0,xi+1=xi+viΔtvi+1=vi−ω2xiΔt
如果在 v v v 的方程中您使用了刚刚计算的值 x i + 1 x_{i+1} xi+1 会怎样?像这样:
x ( t 0 ) = x 0 , x i + 1 = x i + v i Δ t v ( t 0 ) = v 0 , v i + 1 = v i − ω 2 x i + 1 Δ t \begin{aligned} & x\left(t_0\right)=x_0, \quad x_{i+1}=x_i+v_i \Delta t \\ & v\left(t_0\right)=v_0, \quad v_{i+1}=v_i-\omega^2 x_{i+1} \Delta t \\ & \end{aligned} x(t0)=x0,xi+1=xi+viΔtv(t0)=v0,vi+1=vi−ω2xi+1Δt
请注意第二个方程右侧的 x i + 1 x_{i+1} xi+1:这是更新后的值,给出时间间隔结束时的加速度。这种修改后的方案称为欧拉-克罗默方法。
代码实现:
def euler_cromer(state, rhs, dt):mid_state = state + rhs(state)*dt # Euler stepmid_derivs = rhs(mid_state) # updated derivativesnext_state = np.array([mid_state[0], state[1] + mid_derivs[1]*dt])return next_state
模拟数据
w = 2
period = 2*np.pi/w
dt = period/200
T = 800*period
N = round(T/dt)print('The number of time steps is {}.'.format( N ))
print('The time increment is {}'.format( dt ))t = np.linspace(0, T, N)x0 = 2
v0 = 0 num_sol = np.zeros([N,2])
num_sol[0,0] = x0
num_sol[0,1] = v0for i in range(N-1):num_sol[i+1] = euler_cromer(num_sol[i], springmass, dt)
The number of time steps is 160000. The time increment is 0.015707963267948967
首先,得到解析解。然后,您选择绘制振荡运动的前几个周期:数值和解析。
x_an = x0*np.cos(w * t)
iend = 800
fig = plt.figure(figsize=(6,4))
plt.plot(t[:iend], num_sol[:iend, 0], linewidth=2, linestyle='--', label='Numerical solution')
plt.plot(t[:iend], x_an[:iend], linewidth=1, linestyle='-', label='Analytical solution')
plt.xlabel('Time [s]')
plt.ylabel('$x$ [m]')
plt.title('Spring-mass system, with Euler-Cromer method.\n');
该图显示,欧拉-克罗默不存在振幅增大的问题。从这个意义上讲,你应该对此感到满意。但是,如果你绘制一段较长模拟的末尾,你就会发现它确实开始偏离解析解。
istart = 400fig = plt.figure(figsize=(6,4))plt.plot(t[-istart:], num_sol[-istart:, 0], linewidth=2, linestyle='--', label='Numerical solution')
plt.plot(t[-istart:], x_an[-istart:], linewidth=1, linestyle='-', label='Analytical solution')
plt.xlabel('Time [s]')
plt.ylabel('$x$ [m]')
plt.title('Spring-mass system, with Euler-Cromer method. \n');
观察一段很长的运行中的最后几次振荡,即使时间增量很小,也会发现轻微的相位差。因此,尽管欧拉-克罗默方法解决了欧拉方法的一个大问题,但它仍然存在一些错误。它仍然是一阶方法!
👉参阅:计算思维 | 亚图跨际
相关文章:

Python和MATLAB粘性力接触力动态模型半隐式欧拉算法
🎯要点 🎯运动力模型计算制作过程:🖊相机捕捉网球运动图,制定运动数学模型,数值微分运动方程 | 🖊计算运动,欧拉算法离散积分运动,欧拉-克罗默算法微分运动方程 &#…...
webstorm无法识别tsconfig.json引用项目配置文件中的路径别名
问题 vite项目模板中,应用的ts配置内容写在tsconfig.app.json文件中,并在tsconfig.json通过项目引用的方式导入 {"files": [],"references": [{"path": "./tsconfig.app.json"},{"path": "./t…...
qiankun微前端:qiankun+vite+vue3+ts(未完待续..)
目录 什么是微前端 目前现有的微前端 好处 使用 子应用的页面在主应用里显示 什么是微前端 微前端是一种多个团队通过独立发布功能的方式来共同构建现代化 web 应用的技术手段及方法策略。 我的理解就是将一个大型的前端应用拆分成多个模块,每个微前端模块可以由…...

001:开源交易系统开发实战开篇
本专栏采用融入【主力思维】的方法学,包含数据抓取、特征模型开发、历史验证回归测试、每日动态风险评估管理等技术,较大的增强股票投资胜率,让IT开发者拥有一套属于自己思路的专用交易软件。 先简要介绍系统成功和项目,后续持续…...

Pytorch实战(一):LeNet神经网络
文章目录 一、模型实现1.1数据集的下载1.2加载数据集1.3模型训练1.4模型预测 LeNet神经网络是第一个卷积神经网络(CNN),首次采用了卷积层、池化层这两个全新的神经网络组件,接收灰度图像,并输出其中包含的手写数字&…...
RabbitMq的基础及springAmqp的使用
RabbitMq 官网:RabbitMQ: One broker to queue them all | RabbitMQ 什么是MQ? mq就是消息队列,消息队列遵循这先入先出原则。一般用来解决应用解耦,异步消息,流量削峰等问题,实现高性能,高可用…...
uniapp uniCloud云开发
uniCloud概述 uniCloud 是 DCloud 联合阿里云、腾讯云、支付宝云,为开发者提供的基于 serverless 模式和 js 编程的云开发平台。 uniCloud 的 web控制台地址:https://unicloud.dcloud.net.cn 文档:https://doc.dcloud.net.cn/uniCloud/ un…...

智能扫地机,让生活电器更加便民-NV040D扫地机语音方案
一、语音扫地机开发背景: 随着人工智能和物联网技术的飞速发展,智能家居设备已成为现代家庭不可或缺的一部分。其中,扫地机作为家庭清洁的重要工具,更是得到了广泛的关注和应用。 然而,传统的扫地机在功能和使用上仍存…...
【后端面试题】【中间件】【NoSQL】ElasticSearch索引机制和高性能的面试思路
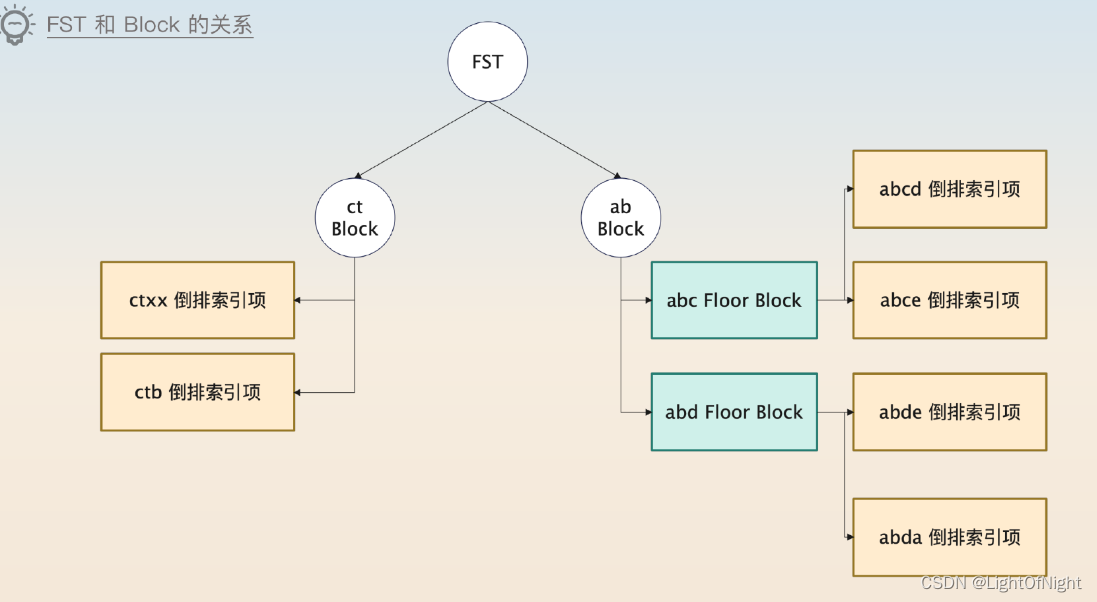
Elasticsearch的索引机制 Elasticsearch使用的是倒排索引,所谓的倒排索引是相对于正排索引而言的。 在一般的文件系统中,索引是文档映射到关键字,而倒排索引则相反,是从关键字映射到文档。 如果没有倒排索引的话,想找…...

【漏洞复现】时空智友ERP updater.uploadStudioFile接口处存在任意文件上传
0x01 产品简介 时空智友ERP是一款基于云计算和大数据技术的企业资源计划管理系统。该系统旨在帮助企业实现数字化转型,提高运营效率、降低成本、增强决策能力和竞争力,时空智友ERP系统涵盖了企业的各个业务领域,包括财务管理、供应链管理、生…...

[leetcode hot 150]第五百三十题,二叉搜索树的最小绝对差
题目: 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其数值等于两值之差的绝对值。 解析: minDiffInBST 方法是主要方法。创建一个 ArrayList 来存储树的节点值。inorderTrave…...

【Docker】可视化平台Portainer
文章目录 Portainer的特点Portainer的安装步骤注意事项 Docker的可视化工具Portainer是一个轻量级的容器管理平台,它为用户提供了一个直观的图形界面来管理Docker环境。以下是关于Portainer的详细介绍和安装步骤: Portainer的特点 轻量级:P…...

MySQL高级-MVCC-原理分析(RR级别)
文章目录 1、RR隔离级别下,仅在事务中第一次执行快照读时生成ReadView,后续复用该ReadView2、总结 1、RR隔离级别下,仅在事务中第一次执行快照读时生成ReadView,后续复用该ReadView 而RR 是可重复读,在一个事务中&…...

压力测试Monkey命令参数和报告分析
目录 常用参数 -p <测试的包名列表> -v 显示日志详细程度 -s 伪随机数生成器的种子值 --throttle < 毫秒> --ignore-crashes 忽略崩溃 --ignore-timeouts 忽略超时 --monitor-native-crashes 监视本地崩溃代码 --ignore-security-exceptions 忽略安全异常 …...
C# Benchmark
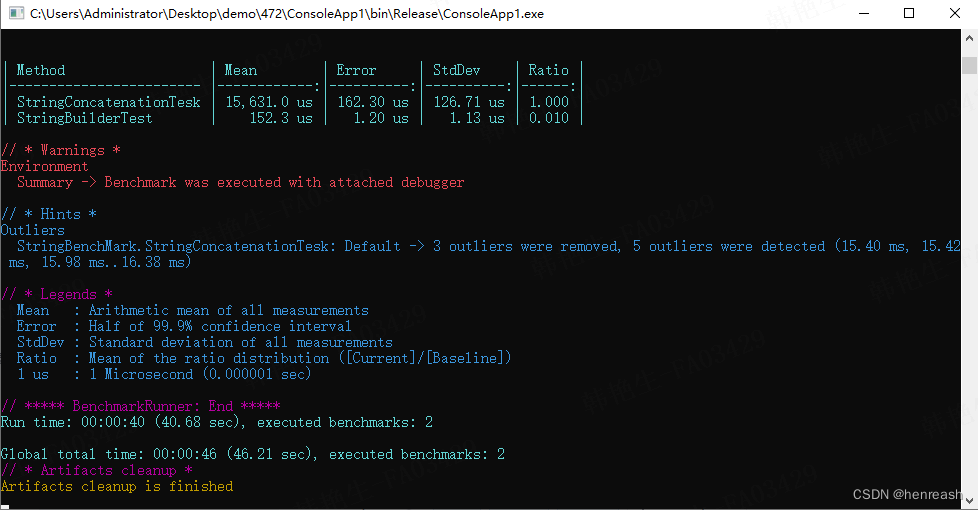
创建控制台项目(或修改现有项目的Main方法代码),Nget导入Benchmark0.13.12,创建测试类: public class StringBenchMark{int[] numbers;public StringBenchMark() {numbers Enumerable.Range(1, 20000).ToArray();}[Be…...
算法金 | 协方差、方差、标准差、协方差矩阵
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 抱个拳,送个礼 1. 方差 方差是统计学中用来度量一组数据分散程度的重要指标。它反映了数据点与其均值之间的偏离程度。在…...
FastAPI教程II
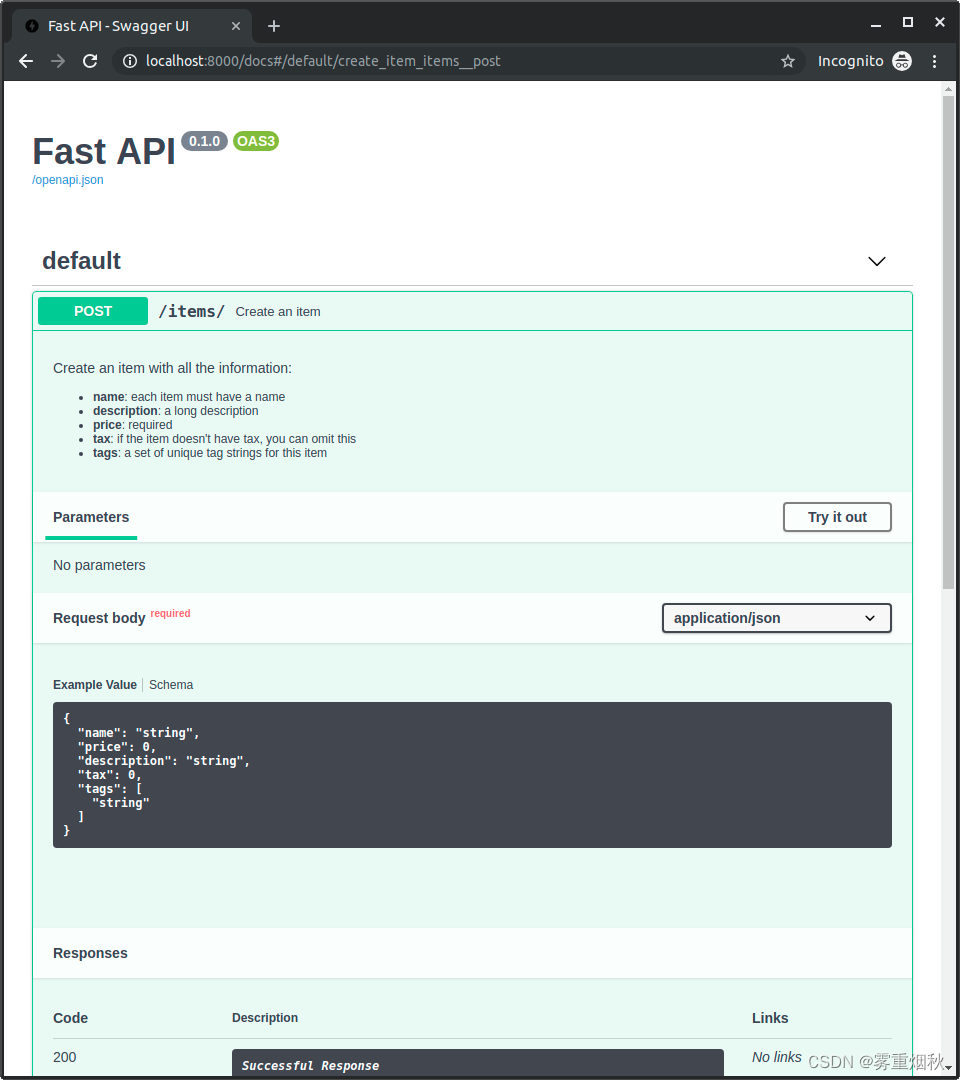
本文参考FastAPI教程https://fastapi.tiangolo.com/zh/tutorial Cookie参数 定义Cookie参数与定义Query和Path参数一样。 具体步骤如下: 导入Cookie:from fastapi import Cookie声明Cookie参数,声明Cookie参数的方式与声明Query和Path参数…...

Facebook的投流技巧有哪些?
相信大家都知道Facebook拥有着巨大的用户群体和高转化率,在国外社交推广中的影响不言而喻。但随着Facebook广告的竞争越来越激烈,在Facebook广告上获得高投资回报率也变得越来越困难。IPIDEA代理IP今天就教大家如何在Facebook上投放广告的技巧࿰…...

Spring Boot 中的微服务监控与管理
微服务的概述 微服务架构的优点和挑战 优点: 灵活性和可扩展性:微服务架构允许每个服务单独部署和扩展,这使得系统可以更灵活地适应不同的业务需求和负载变化。 使团队更加聚焦:每个微服务都有明确的职责,这使得开发团队可以更加聚焦,专注于开发他们的服务。 技术和框…...
模拟卷)
【计算机网络】期末复习(1)模拟卷
一、选择题 1. 电路交换的三个阶段是建立连接、()和释放连接 A. Hello包探测 B. 通信 C. 二次握手 D. 总线连接 2. 一下哪个协议不属于C/S模式() A. SNMP…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
