递推算法计算信号特征
在线算法(在线计算或递推计算)能够在不存储全部数据的情况下逐步更新信号的特征信息,非常适合资源受限的单片机应用场景。
用途:单片机边采集ADC边计算,最终将采集的信号特征计算结果。平台通过长期监控信号特征来确定采集的设备工作正常。用途机台长期监控。
以下是几种常见的信号特征信息计算及其对应的在线算法:
1. 均值(Mean)
递推均值公式
mean n = ( n − 1 ) ⋅ mean n − 1 + x n n \text{mean}_n = \frac{(n-1) \cdot \text{mean}_{n-1} + x_n}{n} meann=n(n−1)⋅meann−1+xn
其中,( n ) 是当前采样点的数量,( x_n ) 是第 ( n ) 个采样值,( \text{mean}_{n-1} ) 是前 ( n-1 ) 个采样值的均值。
2. 均方根(RMS, Root Mean Square)
递推 RMS 公式:
RMS n = ( n − 1 ) ⋅ ( RMS n − 1 ) 2 + x n 2 n \text{RMS}_n = \sqrt{\frac{(n-1) \cdot (\text{RMS}_{n-1})^2 + x_n^2}{n}} RMSn=n(n−1)⋅(RMSn−1)2+xn2
3. 方差(Variance)
递推方差公式:
var n = ( n − 1 ) ⋅ var n − 1 + ( x n − mean n ) ( x n − mean n − 1 ) n \text{var}_n = \frac{(n-1) \cdot \text{var}_{n-1} + (x_n - \text{mean}_n)(x_n - \text{mean}_{n-1})}{n} varn=n(n−1)⋅varn−1+(xn−meann)(xn−meann−1)
4. 标准差(Standard Deviation)
标准差是方差的平方根:
stddev n = var n \text{stddev}_n = \sqrt{\text{var}_n} stddevn=varn
5. 峰峰值(Peak-to-Peak Value)
更新最大值和最小值:
if (x_n > max) max = x_n;
if (x_n < min) min = x_n;
峰峰值计算公式:
peak-to-peak = max − min \text{peak-to-peak} = \text{max} - \text{min} peak-to-peak=max−min
6. 平均绝对偏差(Mean Absolute Deviation, MAD)
递推平均绝对偏差公式:
MAD n = ( n − 1 ) ⋅ MAD n − 1 + ∣ x n − mean n ∣ n \text{MAD}_n = \frac{(n-1) \cdot \text{MAD}_{n-1} + |x_n - \text{mean}_n|}{n} MADn=n(n−1)⋅MADn−1+∣xn−meann∣
7. 信号功率(Power)
递推信号功率公式:
power n = ( n − 1 ) ⋅ power n − 1 + x n 2 n \text{power}_n = \frac{(n-1) \cdot \text{power}_{n-1} + x_n^2}{n} powern=n(n−1)⋅powern−1+xn2
8. 信号能量(Energy)
信号能量是所有样本平方的累加和:
energy n = energy n − 1 + x n 2 \text{energy}_n = \text{energy}_{n-1} + x_n^2 energyn=energyn−1+xn2
示例代码更新
以下是使用递推算法计算上述信号特征信息的示例代码:
#include "stm32f0xx_hal.h"
#include <math.h>// 全局变量
volatile uint32_t count = 0;
volatile float mean = 0;
volatile float variance = 0;
volatile float stddev = 0;
volatile float max = -FLT_MAX;
volatile float min = FLT_MAX;
volatile float mad = 0;
volatile float power = 0;
volatile float energy = 0;
volatile uint8_t trigger_active = 0;// ADC 和定时器句柄
ADC_HandleTypeDef hadc;
TIM_HandleTypeDef htim;// 初始化 ADC
void ADC_Init(void) {__HAL_RCC_ADC1_CLK_ENABLE();hadc.Instance = ADC1;hadc.Init.Resolution = ADC_RESOLUTION_12B;hadc.Init.ScanConvMode = DISABLE;hadc.Init.ContinuousConvMode = DISABLE;hadc.Init.DiscontinuousConvMode = DISABLE;hadc.Init.ExternalTrigConv = ADC_EXTERNALTRIGCONV_T1_TRGO;hadc.Init.DataAlign = ADC_DATAALIGN_RIGHT;hadc.Init.NbrOfConversion = 1;HAL_ADC_Init(&hadc);// 配置 ADC 通道ADC_ChannelConfTypeDef sConfig = {0};sConfig.Channel = ADC_CHANNEL_0;sConfig.Rank = ADC_RANK_CHANNEL_NUMBER;HAL_ADC_ConfigChannel(&hadc, &sConfig);
}// 初始化定时器
void TIM_Init(void) {__HAL_RCC_TIM1_CLK_ENABLE();htim.Instance = TIM1;htim.Init.Prescaler = 8000 - 1; // 1 MHz 时钟,1 kHz 采样率htim.Init.CounterMode = TIM_COUNTERMODE_UP;htim.Init.Period = 1000 - 1; // 1 kHzhtim.Init.ClockDivision = TIM_CLOCKDIVISION_DIV1;HAL_TIM_Base_Init(&htim);// 配置定时器触发 ADCTIM_MasterConfigTypeDef sMasterConfig = {0};sMasterConfig.MasterOutputTrigger = TIM_TRGO_UPDATE;sMasterConfig.MasterSlaveMode = TIM_MASTERSLAVEMODE_DISABLE;HAL_TIMEx_MasterConfigSynchronization(&htim, &sMasterConfig);
}// ADC 转换完成中断服务函数
void HAL_ADC_ConvCpltCallback(ADC_HandleTypeDef* hadc) {if (trigger_active) {uint32_t adc_value = HAL_ADC_GetValue(hadc);float x_n = (float)adc_value;// 更新样本计数count++;// 计算均值float old_mean = mean;mean = ((count - 1) * mean + x_n) / count;// 计算方差variance = ((count - 1) * variance + (x_n - mean) * (x_n - old_mean)) / count;stddev = sqrt(variance);// 更新最大值和最小值if (x_n > max) max = x_n;if (x_n < min) min = x_n;// 计算平均绝对偏差mad = ((count - 1) * mad + fabs(x_n - mean)) / count;// 计算信号功率power = ((count - 1) * power + x_n * x_n) / count;// 计算信号能量energy += x_n * x_n;}
}// 触发信号检测函数
void check_trigger_signal(void) {if (/* 检测到触发信号 */) {trigger_active = 1;HAL_ADC_Start_IT(&hadc);HAL_TIM_Base_Start(&htim);} else {trigger_active = 0;HAL_ADC_Stop_IT(&hadc);HAL_TIM_Base_Stop(&htim);}
}// 主函数
int main(void) {HAL_Init();ADC_Init();TIM_Init();while (1) {check_trigger_signal();// 其他处理}
}
在这个示例代码中,我们展示了如何使用递推算法来计算多个信号特征信息,包括均值、方差、标准差、最大值、最小值、平均绝对偏差、信号功率和能量。这些算法在每次新的采样点到达时更新,无需存储所有数据,适用于单片机环境。
相关文章:

递推算法计算信号特征
在线算法(在线计算或递推计算)能够在不存储全部数据的情况下逐步更新信号的特征信息,非常适合资源受限的单片机应用场景。 用途:单片机边采集ADC边计算,最终将采集的信号特征计算结果…...

spring-boot-configuration-processor注释处理器
开源项目SDK:https://github.com/mingyang66/spring-parent 个人文档:https://mingyang66.github.io/raccoon-docs/#/ spring-boot-configuration-processor是springboot提供的一个注释处理器(annotation processor),它用于在编译…...

Python和MATLAB粘性力接触力动态模型半隐式欧拉算法
🎯要点 🎯运动力模型计算制作过程:🖊相机捕捉网球运动图,制定运动数学模型,数值微分运动方程 | 🖊计算运动,欧拉算法离散积分运动,欧拉-克罗默算法微分运动方程 &#…...
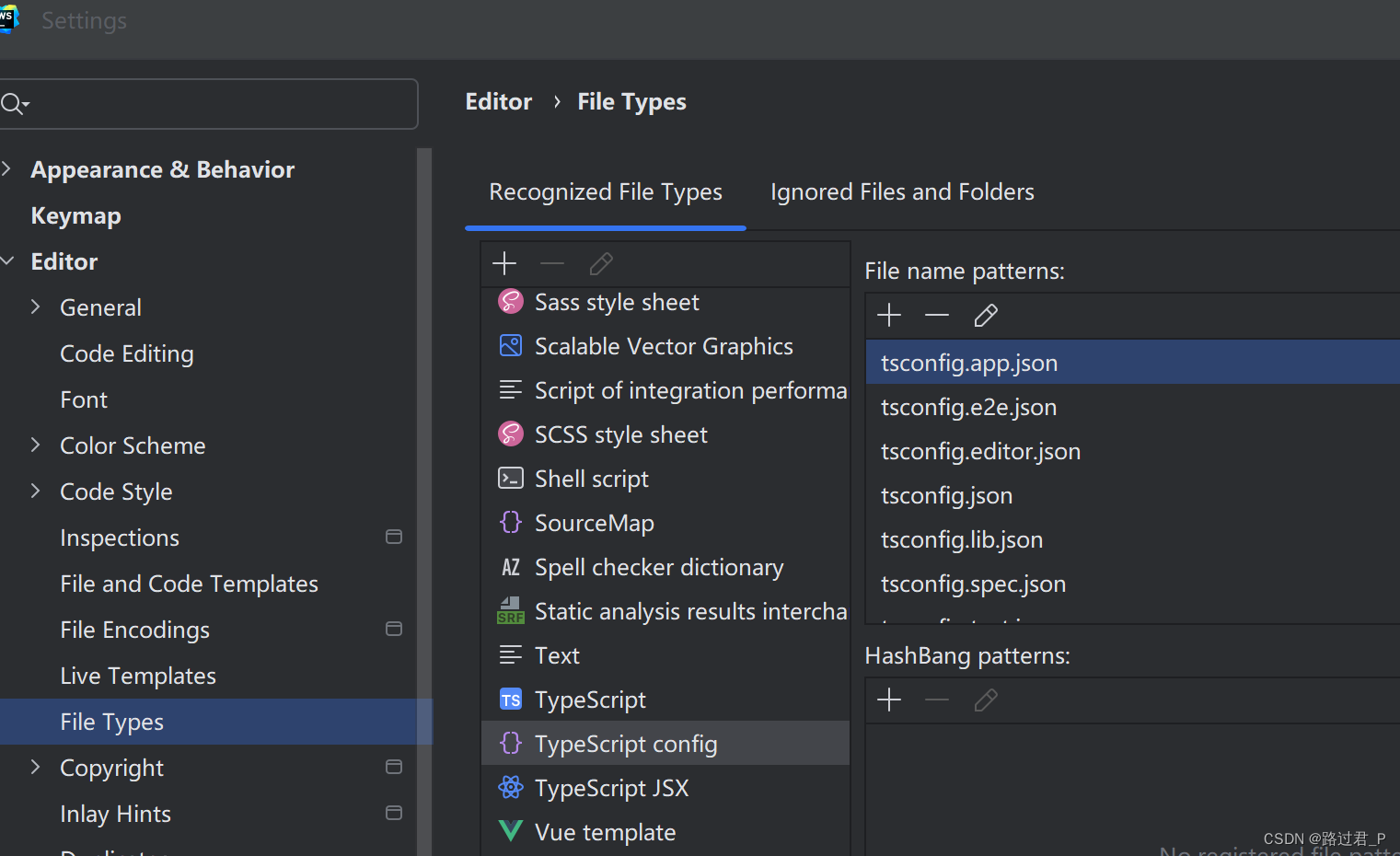
webstorm无法识别tsconfig.json引用项目配置文件中的路径别名
问题 vite项目模板中,应用的ts配置内容写在tsconfig.app.json文件中,并在tsconfig.json通过项目引用的方式导入 {"files": [],"references": [{"path": "./tsconfig.app.json"},{"path": "./t…...
qiankun微前端:qiankun+vite+vue3+ts(未完待续..)
目录 什么是微前端 目前现有的微前端 好处 使用 子应用的页面在主应用里显示 什么是微前端 微前端是一种多个团队通过独立发布功能的方式来共同构建现代化 web 应用的技术手段及方法策略。 我的理解就是将一个大型的前端应用拆分成多个模块,每个微前端模块可以由…...

001:开源交易系统开发实战开篇
本专栏采用融入【主力思维】的方法学,包含数据抓取、特征模型开发、历史验证回归测试、每日动态风险评估管理等技术,较大的增强股票投资胜率,让IT开发者拥有一套属于自己思路的专用交易软件。 先简要介绍系统成功和项目,后续持续…...

Pytorch实战(一):LeNet神经网络
文章目录 一、模型实现1.1数据集的下载1.2加载数据集1.3模型训练1.4模型预测 LeNet神经网络是第一个卷积神经网络(CNN),首次采用了卷积层、池化层这两个全新的神经网络组件,接收灰度图像,并输出其中包含的手写数字&…...
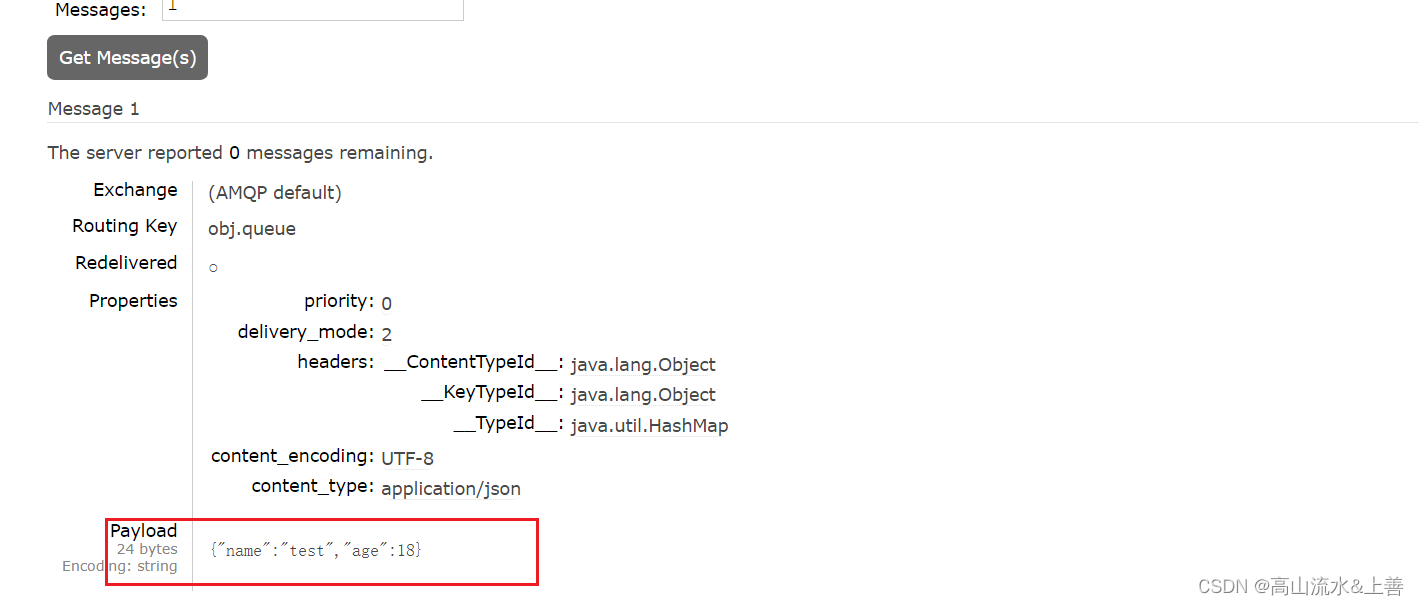
RabbitMq的基础及springAmqp的使用
RabbitMq 官网:RabbitMQ: One broker to queue them all | RabbitMQ 什么是MQ? mq就是消息队列,消息队列遵循这先入先出原则。一般用来解决应用解耦,异步消息,流量削峰等问题,实现高性能,高可用…...
uniapp uniCloud云开发
uniCloud概述 uniCloud 是 DCloud 联合阿里云、腾讯云、支付宝云,为开发者提供的基于 serverless 模式和 js 编程的云开发平台。 uniCloud 的 web控制台地址:https://unicloud.dcloud.net.cn 文档:https://doc.dcloud.net.cn/uniCloud/ un…...

智能扫地机,让生活电器更加便民-NV040D扫地机语音方案
一、语音扫地机开发背景: 随着人工智能和物联网技术的飞速发展,智能家居设备已成为现代家庭不可或缺的一部分。其中,扫地机作为家庭清洁的重要工具,更是得到了广泛的关注和应用。 然而,传统的扫地机在功能和使用上仍存…...
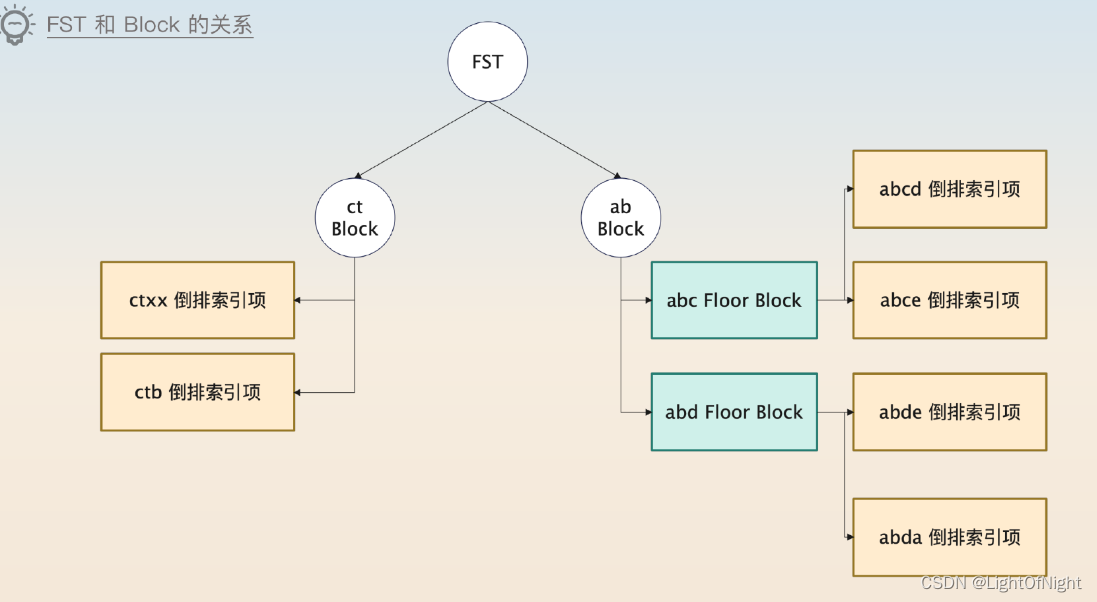
【后端面试题】【中间件】【NoSQL】ElasticSearch索引机制和高性能的面试思路
Elasticsearch的索引机制 Elasticsearch使用的是倒排索引,所谓的倒排索引是相对于正排索引而言的。 在一般的文件系统中,索引是文档映射到关键字,而倒排索引则相反,是从关键字映射到文档。 如果没有倒排索引的话,想找…...

【漏洞复现】时空智友ERP updater.uploadStudioFile接口处存在任意文件上传
0x01 产品简介 时空智友ERP是一款基于云计算和大数据技术的企业资源计划管理系统。该系统旨在帮助企业实现数字化转型,提高运营效率、降低成本、增强决策能力和竞争力,时空智友ERP系统涵盖了企业的各个业务领域,包括财务管理、供应链管理、生…...

[leetcode hot 150]第五百三十题,二叉搜索树的最小绝对差
题目: 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其数值等于两值之差的绝对值。 解析: minDiffInBST 方法是主要方法。创建一个 ArrayList 来存储树的节点值。inorderTrave…...

【Docker】可视化平台Portainer
文章目录 Portainer的特点Portainer的安装步骤注意事项 Docker的可视化工具Portainer是一个轻量级的容器管理平台,它为用户提供了一个直观的图形界面来管理Docker环境。以下是关于Portainer的详细介绍和安装步骤: Portainer的特点 轻量级:P…...

MySQL高级-MVCC-原理分析(RR级别)
文章目录 1、RR隔离级别下,仅在事务中第一次执行快照读时生成ReadView,后续复用该ReadView2、总结 1、RR隔离级别下,仅在事务中第一次执行快照读时生成ReadView,后续复用该ReadView 而RR 是可重复读,在一个事务中&…...

压力测试Monkey命令参数和报告分析
目录 常用参数 -p <测试的包名列表> -v 显示日志详细程度 -s 伪随机数生成器的种子值 --throttle < 毫秒> --ignore-crashes 忽略崩溃 --ignore-timeouts 忽略超时 --monitor-native-crashes 监视本地崩溃代码 --ignore-security-exceptions 忽略安全异常 …...
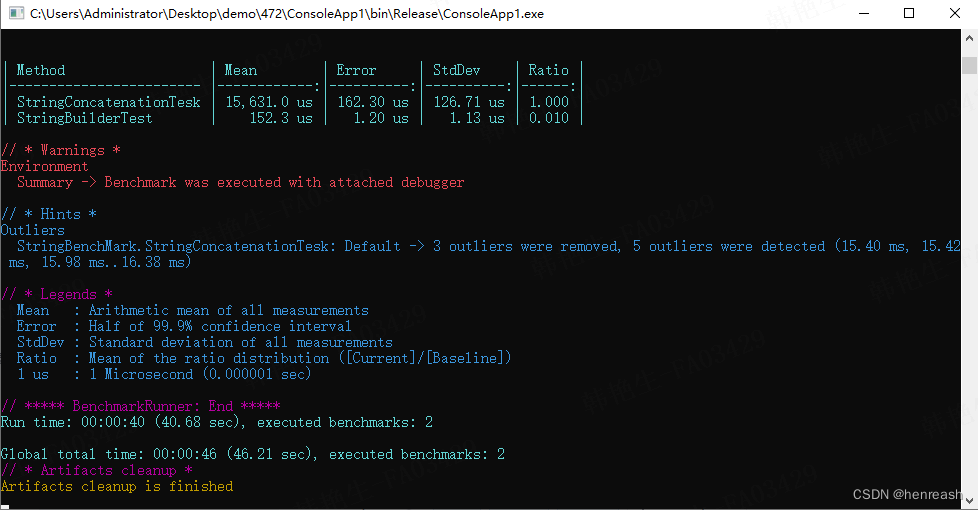
C# Benchmark
创建控制台项目(或修改现有项目的Main方法代码),Nget导入Benchmark0.13.12,创建测试类: public class StringBenchMark{int[] numbers;public StringBenchMark() {numbers Enumerable.Range(1, 20000).ToArray();}[Be…...
算法金 | 协方差、方差、标准差、协方差矩阵
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 抱个拳,送个礼 1. 方差 方差是统计学中用来度量一组数据分散程度的重要指标。它反映了数据点与其均值之间的偏离程度。在…...
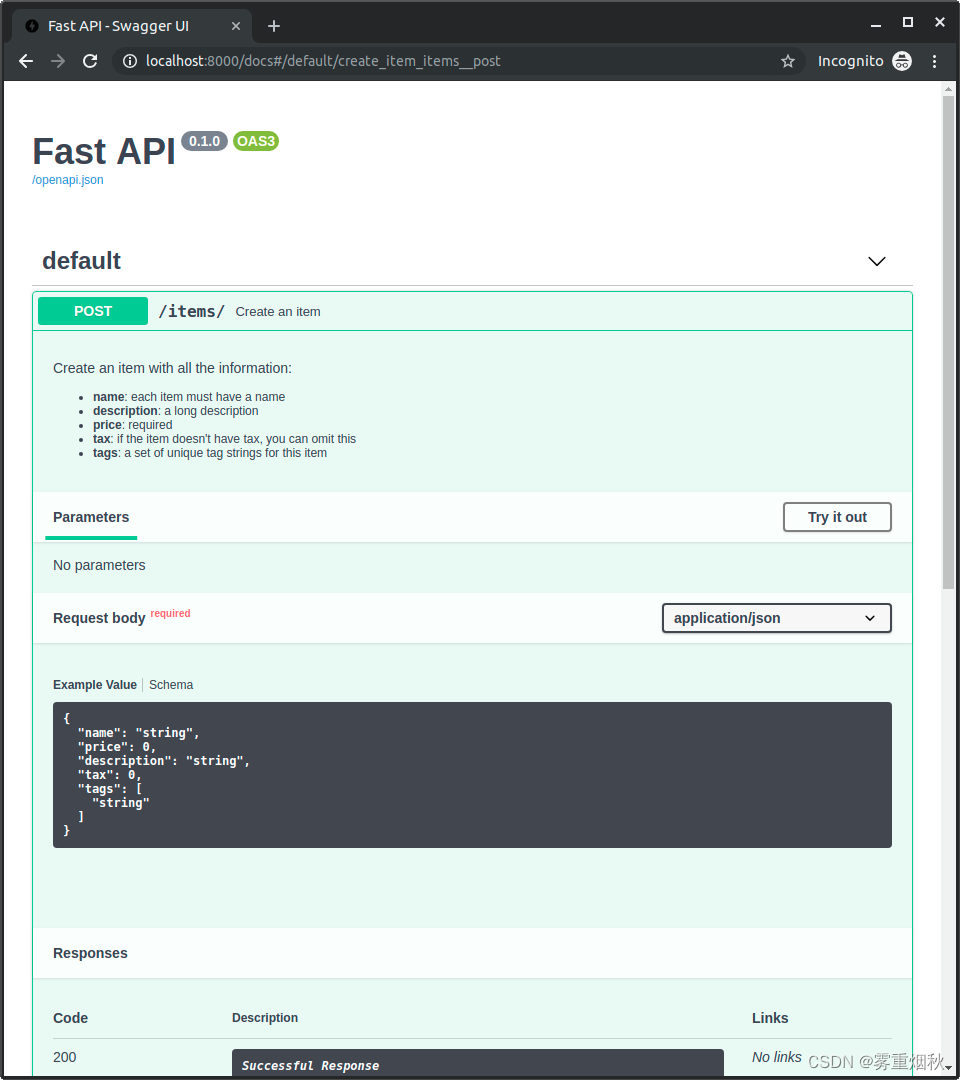
FastAPI教程II
本文参考FastAPI教程https://fastapi.tiangolo.com/zh/tutorial Cookie参数 定义Cookie参数与定义Query和Path参数一样。 具体步骤如下: 导入Cookie:from fastapi import Cookie声明Cookie参数,声明Cookie参数的方式与声明Query和Path参数…...

Facebook的投流技巧有哪些?
相信大家都知道Facebook拥有着巨大的用户群体和高转化率,在国外社交推广中的影响不言而喻。但随着Facebook广告的竞争越来越激烈,在Facebook广告上获得高投资回报率也变得越来越困难。IPIDEA代理IP今天就教大家如何在Facebook上投放广告的技巧࿰…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
