排序(堆排序、快速排序、归并排序)-->深度剖析(二)
前言
前面介绍了冒泡排序、选择排序、插入排序、希尔排序,作为排序中经常用到了算法,还有堆排序、快速排序、归并排序
堆排序(HeaSort)
堆排序的概念
堆排序是一种有效的排序算法,它利用了完全二叉树的特性。在C语言中,堆排序通常通过构建一个最大堆(或最小堆),然后逐步调整堆结构,最终实现排序。
代码实现
堆排序是一种基于二叉堆的排序算法,它通过将待排序的元素构建成一个二叉堆,然后逐步移除堆顶元素并将其放置在数组的尾部,同时维护堆的性质,直至所有元素都被排序。
注意:第一个for循环中的(n-1-1)/ 2 的含义
- 第一个减1是由n-1个元素
- 第二个减1是除以2是父亲节点。以为我们调整的是每一个根节点。(非叶子节点)
//堆排序
void HeapSort(int* a, int n)
{//建堆for(int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a,n,i);}//排序int end = n - 1;while(end > 0){Swap(&a[end], &a[0]);AdjustDown(a, end, 0);--end;}
}其中AdjustDown是建立堆的函数,我们要建立一个大堆,将替换到上上面的小值,向下调整,保持大堆的结构。
代码如下:
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}}
堆排序的复杂度分析
堆排序是一种常用的排序算法,其时间复杂度通常为O(nlogn)。在C语言中实现堆排序时,时间复杂度的分析主要涉及到两个阶段:构建初始堆和进行堆排序。
- 构建初始堆:从最后一个非叶子节点开始,逐步向上调整,直到根节点满足堆的性质。这个过程的时间复杂度为
O(n),因为需要对每个非叶子节点进行一次调整。 - 进行堆排序:堆排序的过程涉及到多次交换堆顶元素和最后一个元素,并对剩余的元素进行调整。每次交换后,堆的大小减一,并对新的堆顶元素进行调整。这个过程的时间复杂度为
O(nlogn),因为每次调整的时间复杂度为O(logn),总共需要进行n-1次调整。
快速排序(Quick Sort)
快速排序的概念
快速排序(Quick Sort)是一种高效的排序算法,它的基本思想是通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,然后再分别对这两部分记录继续进行排序,以达到整个序列有序的目的。在C语言中,快速排序的实现通常涉及到递归函数的编写,以及对数组进行分区(partition)操作。
霍尔版本(hoare)

在这里我们是要,定义一个关键字(keyi)进行分区,然后分别向左右进行递归。
代码实现
int part1(int* a, int left, int right)
{int mid = GetmidNum(a,left,right);Swap(&a[left], &a[mid]);int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi])right--;while (left < right && a[left] <=a[keyi])left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;return keyi;
}
挖坑法
挖坑法类似于霍尔方法,挖坑就是记住关键字,保证关键字就是一个坑位,比关键字值小(大)的时候就入坑位,此时,这个值位置作为新的坑位直至两个前后指针指向同一个坑位。

代码实现
int part2(int* a, int left, int right)
{int mid = GetmidNum(a, left, right);Swap(&a[left], &a[mid]);int keyi = a[left];int hole = left;while (left < right){while (left < right && a[right] >= keyi)right--;Swap(&a[hole], &a[right]);hole = right;while (left < right && a[left] <= keyi)left++;Swap(&a[hole], &a[left]);hole = left;}Swap(&keyi, &a[hole]);keyi = left;return keyi; }
前后指针法
-
prev指针初始化为数组的开始位置,cur指针初始化为prev的下一位置。 -
cur指针向前遍历数组,寻找小于或等于基准值的元素,而prev指针则跟随cur指针的移动,直到cur找到一个小于基准值的元素。 -
一旦找到这样的元素,
prev和cur指针之间的元素都会被交换,然后cur指针继续向前移动,直到找到下一个小于基准值的元素,或者到达数组的末尾。最后,基准值会被放置在prev指针当前的位置,完成一次排序

代码实现
int part3(int* a, int left, int right)
{int mid = GetmidNum(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;int cur = left + 1;int prev = left;while (cur <= right){while (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}递归实现
以上都是递归方法,通过调用分区进行排序。
void QuickSort(int* a, int left, int right)
{if (left >= right)return;int key = part3(a, left, right);QuickSort(a, left, key - 1);QuickSort(a, key + 1, right);}
快速排序迭代实现(利用栈)参考:栈和队列
基本步骤
- 初始化栈:创建一个空栈,用于存储待排序子数组的起始和结束索引。
- 压栈:将整个数组的起始和结束索引作为一对入栈。
- 循环处理,在栈非空时,重复以下步骤:
- 弹出一对索引(即栈顶元素)来指定当前要处理的子数组。
- 选择子数组的一个元素作为枢轴(pivot)进行分区。
- 进行分区操作,这会将子数组划分为比枢轴小的左侧部分和比枢轴大的
代码实现
void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STpush(&st, left);STpush(&st, right);while (!STEmpty(&st)){int end = STTop(&st);STPop(&st);int begin = STTop(&st);STPop(&st);int keyi = part3(a, begin, end);if (keyi + 1 < end){STpush(&st, keyi + 1);STpush(&st, end);}if (begin < keyi - 1){STpush(&st, begin);STpush(&st, keyi - 1);}}STDestroy(&st);
}
快速排序的优化
优化角度从两个方面切入
- 在选择关键字的(基准值)时候,如果我们碰到了,有序数组,那么就会,减低排序效率。
- 方法一:三数取中,即区三个关键字先进行排序,将中间数作为关键字,一般取左端右端和中间值。
- 方法二:随机值。利用随机数生成。
三数取中代码实现
int GetmidNum(int* a, int begin, int end)
{int mid = (begin + end) / 2;if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if(a[end]<a[begin]){return begin;}else{return end;}}else //a[begin]>a[mid]{if (a[begin] < a[end]){return begin;}else if (a[end] < a[mid]){return mid;}else{return end;}}随机选 key(下标) 代码实现
srand(time(0));
int randi = left + (rand() % (right - left));
Swap(&a[left], &a[randi]);
快速排序复杂度分析
- 在平均情况下,快速排序的时间复杂度为O(n log n),这是因为每次划分都能够将数组分成大致相等的两部分,从而实现高效排序。在最坏情况下,快速排序的时间复杂度为O(n^2)
- 除了递归调用的栈空间之外,不需要额外的存储空间,因此空间复杂度是O(log n)。在最坏情况下,快速排序的时间复杂度可能是 O(n),这是因为在最坏情况下,递归堆栈空间可能会增长到线性级别。
根据上述描述,优化快速排序是必要的。
归并排序(Merge Sort)

归并排序的概念
归并排序(Merge Sort)是一种基于分治策略的排序算法,它将待排序的序列分为两个或以上的子序列,对这些子序列分别进行排序,然后再将它们合并为一个有序的序列。归并排序的基本思想是将待排序的序列看作是一系列长度为1的有序序列,然后将相邻的有序序列段两两归并,形成长度为2的有序序列,以此类推,最终得到一个长度为n的有序序列。
基本操作:
- 分解:将序列每次折半划分,递归实现,直到子序列的大小为1。
- 合并:将划分后的序列段两两合并后排序。在每次合并过程中,都是对两个有序的序列段进行合并,然后排序。这两个有序序列段分别为
R[low, mid]和R[mid+1, high]。先将他们合并到一个局部的暂存数组R2中,合并完成后再将R2复制回R中。
代码实现(递归)
void _MergeSort(int* a, int* tmp, int begin, int end)
{if (begin >= end)return;int mid = (begin + end) / 2;_MergeSort(a, tmp, begin, mid - 1);_MergeSort(a, tmp, mid + 1, end);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] > a[begin2]){tmp[i++] = a[begin2++];}else{tmp[i++] = a[begin1++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, tmp, 0, n-1);free(tmp);
}
代码实现(迭代)
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i =2* gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int j = i;if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n-1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp);
}
归并排序复杂度分析
- 时间复杂度是 O(n log n),其中 n 是待排序元素的数量。这个时间复杂度表明,归并排序的执行速度随着输入大小的增加而线性增加,但不会超过对数级的增长。
- 空间复杂度为 O(n),在数据拷贝的时候malloc一个等大的数组。
总结
p[j++] = a[begin2++];
}
}
while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;
}
free(tmp);
}
## 归并排序复杂度分析* 时间复杂度是 O(n log n),其中 n 是待排序元素的数量。这个时间复杂度表明,归并排序的执行速度随着输入大小的增加而线性增加,但不会超过对数级的增长。
* 空间复杂度为 O(n),在数据拷贝的时候malloc一个等大的数组。# 总结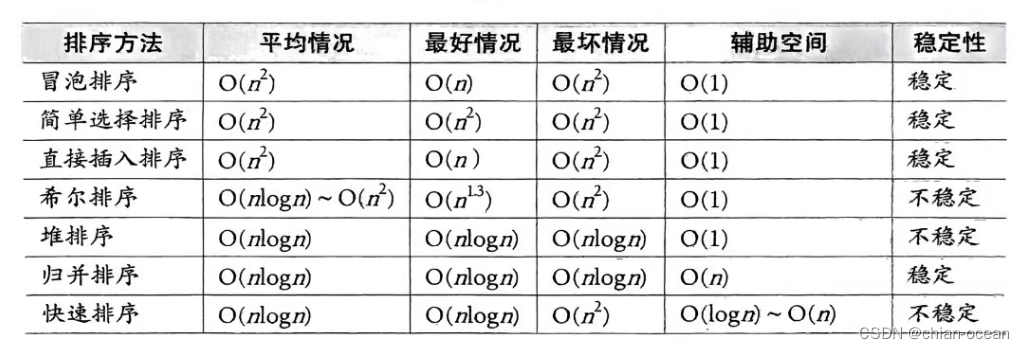相关文章:

排序(堆排序、快速排序、归并排序)-->深度剖析(二)
前言 前面介绍了冒泡排序、选择排序、插入排序、希尔排序,作为排序中经常用到了算法,还有堆排序、快速排序、归并排序 堆排序(HeaSort) 堆排序的概念 堆排序是一种有效的排序算法,它利用了完全二叉树的特性。在C语言…...

七一建党节|热烈庆祝中国共产党成立103周年!
时光荏苒,岁月如梭。 在这热情似火的夏日, 我们迎来了中国共产党成立103周年的重要时刻。 这是一个值得全体中华儿女共同铭记和庆祝的日子, 也是激励我们不断前进的重要时刻。 103年, 风雨兼程,砥砺前行。 从嘉兴…...

Spring Boot应用知识梳理
一.简介 Spring Boot 是一个用于快速开发基于 Spring 框架的应用程序的工具。它简化了基于 Spring 的应用程序的配置和部署过程,提供了一种快速、便捷的方式来构建独立的、生产级别的 Spring 应用程序。 Spring Boot 的一些主要优点包括: 1. 简化配置…...

Spring中利用重载与静态分派
Spring中利用重载与静态分派 在Java和Spring框架中,重载(Overloading)和静态分派(Static Dispatch)是两个非常重要的概念,它们在处理类方法选择和执行过程中扮演着关键角色。本文旨在深入探讨Spring环境下…...

文本三剑客之awk:
文本三剑客awk: grep 查 sed 增删改查 主要:增改 awk 按行取列 awk awk默认的分隔符:空格,tab键,多个空格自动压缩为一个。 awk的工作原理:根据指令信息,逐行的读取文本内容,然…...

SpringSecurity-授权示例
用户基于权限进行授权 定义用户与权限 authorities()。 package com.cms.config;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.security.core.userdetails.User; import…...

选哪个短剧系统源码好:全面评估与决策指南
在短剧内容创作和分享日益流行的今天,选择合适的短剧系统源码对于构建一个成功的短剧平台至关重要。短剧系统源码不仅关系到平台的稳定性和用户体验,还直接影响到内容创作者和观众的互动质量。本文将提供一份全面的评估指南,帮助您在众多短剧…...

AI时代的软件工程:挑战与改变
人工智能(AI)正以惊人的速度改变着我们的生活和工作方式。作为与AI关系最为密切的领域之一,软件工程正经历着深刻的转变。 1 软件工程的演变 软件工程的起源 软件工程(Software Engineering)是关于如何系统化、规范化地…...

Zuul介绍
Zuul 是 Netflix 开源的一个云平台网络层代理,它主要用于路由、负载均衡、中间件通信和动态路由。Zuul 本质上是一个基于 JVM 的网关,它提供了以下功能: 1.路由:Zuul 允许客户端和服务器之间的所有入站和出站请求通过一个中心化的…...
7-1作业
1.实验目的:完成字符收发 led.h #ifndef __GPIO_H__ #define __GPIO_H__#include "stm32mp1xx_rcc.h" #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_uart.h"//RCC,GPIO,UART初始化 void init();//字符数据发送 void set_tt…...

ElasticSearch安装、配置详细步骤
一、环境及版本介绍 操作系统: Windows 10 软件版本: elasticsearch-7.17.22、kibana-7.17.22、IK-7.17.22 开发环境选择软件版本应提前考虑正式系统环境,否则会产生软件与服务器环境不兼容的问题出现,ElasticSearch与环境支持…...
【Mybatis 与 Spring】事务相关汇总
之前分享的几篇文章可以一起看,形成一个体系 【Mybatis】一级缓存与二级缓存源码分析与自定义二级缓存 【Spring】Spring事务相关源码分析 【Mybatis】Mybatis数据源与事务源码分析 Spring与Mybaitis融合 SpringManagedTransaction: org.mybatis.spri…...
)
Leetcode 2065. 最大化一张图中的路径价值(DFS / 最短路)
Leetcode 2065. 最大化一张图中的路径价值 暴力DFS 容易想到,从0点出发DFS,期间维护已经走过的距离(时间)和途径点的权值之和,若访问到0点则更新答案,若下一步的距离与已走过的距离和超出了maxTime&#…...
SeeSR: Towards Semantics-Aware Real-World Image Super-Resolution
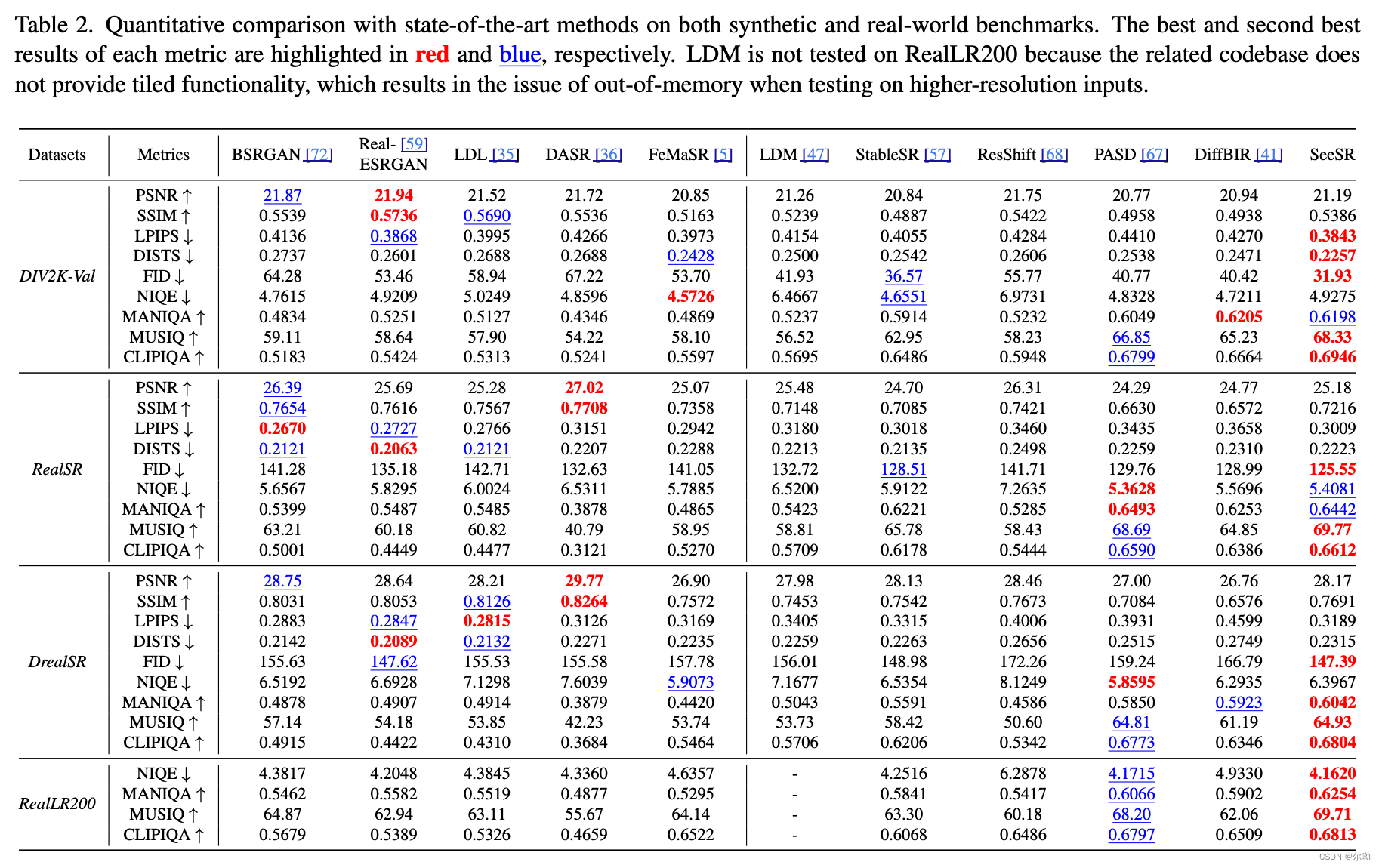
CVPR2024 香港理工大学&OPPO&bytedancehttps://github.com/cswry/SeeSR?tabreadme-ov-file#-licensehttps://arxiv.org/pdf/2311.16518#page5.80 问题引入 因为有些LR退化情况比较严重,所以超分之后的结果会出现语义的不一致的情况,所以本文训…...
七月论文审稿GPT第5版:拿我司七月的早期paper-7方面review数据集微调LLama 3
前言 llama 3出来后,为了通过paper-review的数据集微调3,有以下各种方式 不用任何框架 工具 技术,直接微调原生的llama 3,毕竟也有8k长度了 效果不期望有多高,纯作为baseline通过PI,把llama 3的8K长度扩展…...

盘古5.0,靠什么去解最难的题?
文|周效敬 编|王一粟 当大模型的竞争开始拼落地,商业化在B端和C端都展开了自由生长。 在B端,借助云计算向千行万业扎根;在C端,通过软件App和智能终端快速迭代。 在华为,这家曾经以通信行业起…...
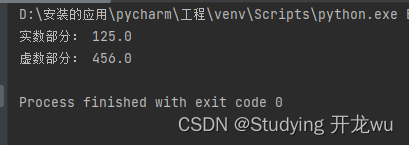
2.3章节Python中的数值类型
1.整型数值 2.浮点型数值 3.复数 Python中的数值类型清晰且丰富,主要分为以下几种类型,每种类型都有其特定的用途和特性。 一、整型数值 1.定义:整数类型用于表示整数值,如1、-5、100等。 2.特点: Python 3中的…...

每日Attention学习7——Frequency-Perception Module
模块出处 [link] [code] [ACM MM 23] Frequency Perception Network for Camouflaged Object Detection 模块名称 Frequency-Perception Module (FPM) 模块作用 获取频域信息,更好识别伪装对象 模块结构 模块代码 import torch import torch.nn as nn import to…...
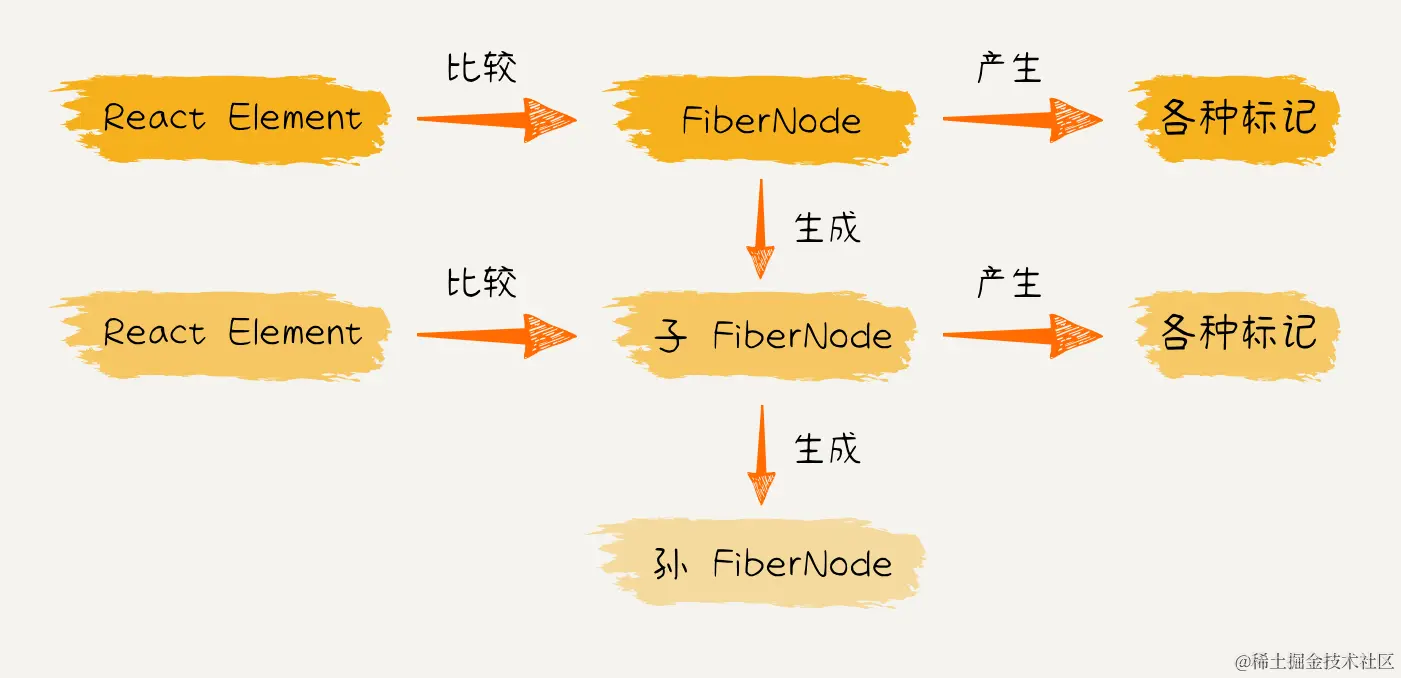
【从0实现React18】 (五) 初探react mount流程 完成核心递归流程
更新流程的目的: 生成wip fiberNode树标记副作用flags 更新流程的步骤: 递:beginWork归:completeWork 在 上一节 ,我们探讨了 React 应用在首次渲染或后续更新时的整体更新流程。在 Reconciler 工作流程中ÿ…...
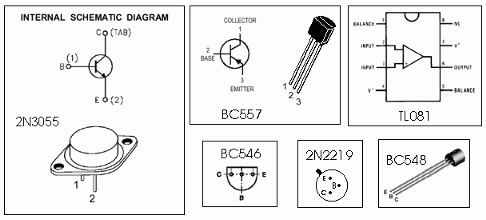
0-30 VDC 稳压电源,电流控制 0.002-3 A
怎么运行的 首先,有一个次级绕组额定值为 24 V/3 A 的降压电源变压器,连接在电路输入点的引脚 1 和 2 上。(电源输出的质量将直接影响与变压器的质量成正比)。变压器次级绕组的交流电压经四个二极管D1-D4组成的电桥整流。桥输出端…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
