【算法刷题 | 动态规划14】6.28(最大子数组和、判断子序列、不同的子序列)

文章目录
- 35.最大子数组和
- 35.1题目
- 35.2解法:动规
- 35.2.1动规思路
- 35.2.2代码实现
- 36.判断子序列
- 36.1题目
- 36.2解法:动规
- 36.2.1动规思路
- 36.2.2代码实现
- 37.不同的子序列
- 37.1题目
- 37.2解法:动规
- 37.2.1动规思路
- 37.2.2代码实现
35.最大子数组和
35.1题目
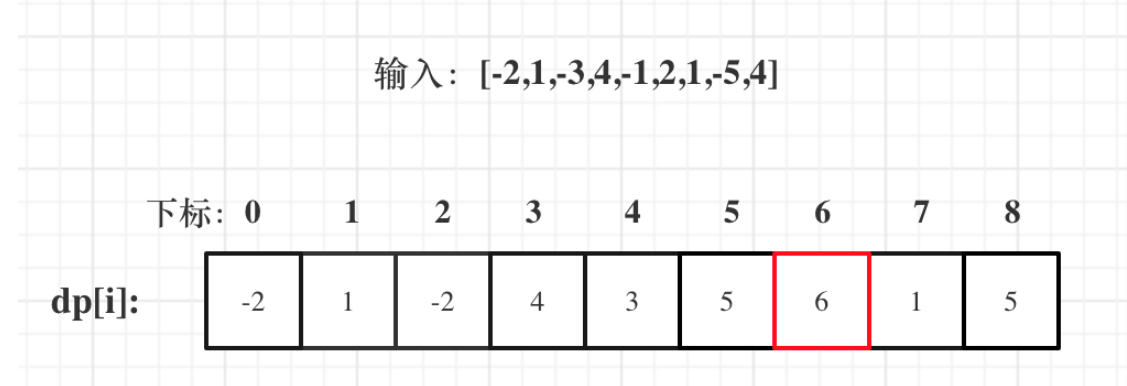
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
- 示例一:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6
- 示例二:
输入:nums = [1]
输出:1
35.2解法:动规
35.2.1动规思路
-
确定dp数组以及下标含义:
dp[i]:下标为i的子数组的最大子数组和为dp[i]
-
确定递推公式:dp[i]=Math.max( dp[i-1]+nums[i],nums[i])
-
dp数组初始化:dp[0]=Math.max(0,nums[i])
-
确定遍历顺序:从前往后
-
举例推导:
35.2.2代码实现
public int maxSubArray(int[] nums) {int[] dp=new int[nums.length];int result=nums[0];dp[0]=nums[0];for(int i=1;i<nums.length;i++){dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);result=Math.max(result,dp[i]);}return result;}
36.判断子序列
36.1题目
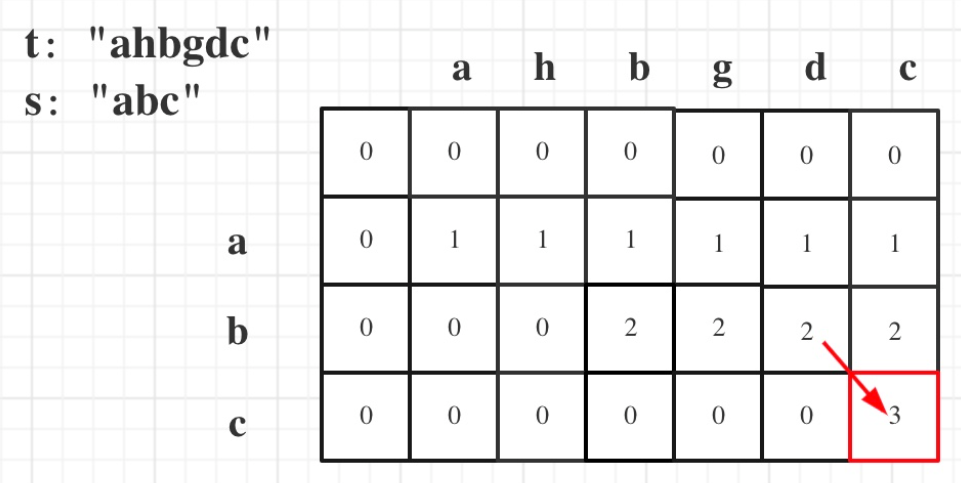
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, … , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
- 示例一:
输入:s = "abc", t = "ahbgdc"
输出:true
- 示例二:
输入:s = "axc", t = "ahbgdc"
输出:false
36.2解法:动规
36.2.1动规思路
-
确定dp数组以及下标含义:
dp(i)(j):表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同的子序列的长度为dp(i)(j)
-
确定递推公式:
2.1 s[i-1]=t[j-1]:t中找到了一个字符,在s中也出现,即dp(i)(j)=dp(i-1)(j-1)+1
2.2 s[i-1]!=t[j-1]:t下标j-1位置的字符和s下标i-1位置的字符不同,即dp(i)(j)=dp(i)(j-1)
-
dp数组初始化:dp(i)(0)和dp(0)(j)位置的元素没有意义
-
确定遍历顺序:从上到下
-
举例推导:
36.2.2代码实现
public boolean isSubsequence(String s, String t) {int[][] dp=new int[s.length()+1][t.length()+1];for(int i=1;i<=s.length();i++){for(int j=1;j<=t.length();j++){if(s.charAt(i-1)==t.charAt(j-1)){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=dp[i][j-1];}}}return dp[s.length()][t.length()]==s.length();}
37.不同的子序列
37.1题目
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
- 示例一:
输入:s = "rabbbit", t = "rabbit"
输出:3
解释:
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit
- 示例二:
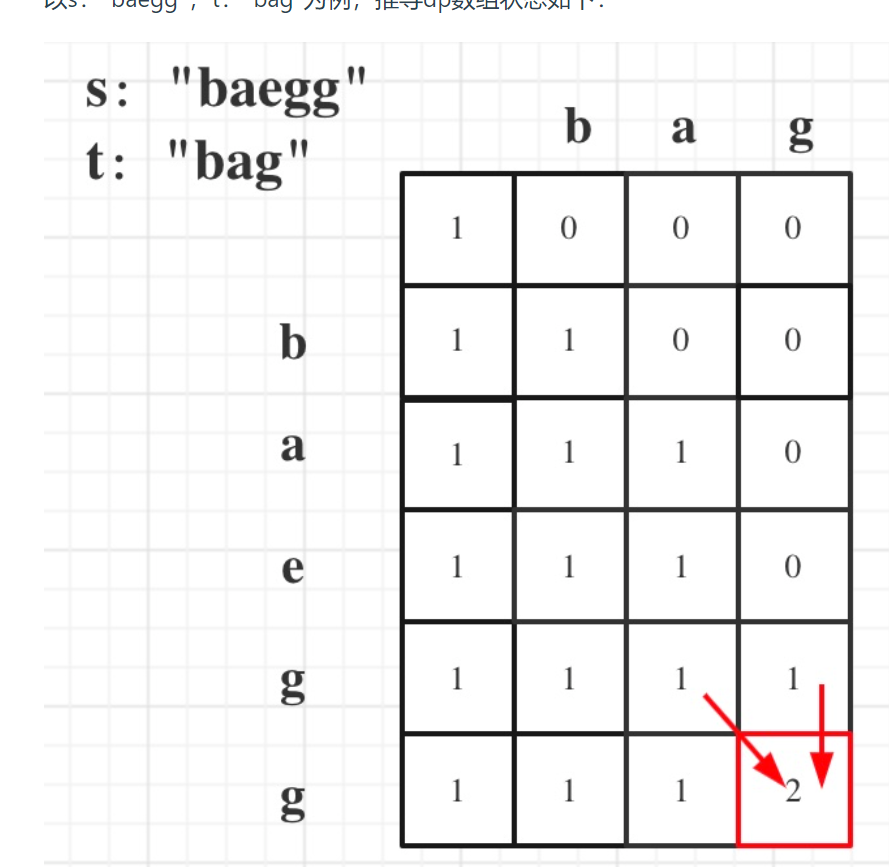
输入:s = "babgbag", t = "bag"
输出:5
解释:
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag
37.2解法:动规
37.2.1动规思路
-
求解:求子序列s组装成t的几种方法!!!
-
确定dp数组以及下标含义:
dp(i)(j):以下标i-1为结尾的s子序列中 出现 以下标j-1为结尾的t子序列的个数 为dp(i)(j)
-
确定递推公式:
3.1 s[i-1]=j[j-1]:两种情况,取s[i-1]或不取,即dp(i)(j)=dp(i-1)(j-1)+dp(i-1)(j)
3.2 s[i-1]!=[j-1]:只能不取s[i-1],即dp(i)(j)=dp(i-1)(j)
-
dp数组初始化:
dp(i)(0):子序列s组装成空串的方法肯定有一种
dp(0)(j):无意义
-
确定遍历顺序:从上到下
-
举例推导:
37.2.2代码实现
public int numDistinct(String s, String t) {int[][] dp=new int[s.length()+1][t.length()+1];//初始化for(int i=0;i<=s.length();i++){dp[i][0]=1;}for(int i=1;i<=s.length();i++){for(int j=1;j<=t.length();j++){if(s.charAt(i-1)==t.charAt(j-1)){//两种情况:取/不取dp[i][j]=dp[i-1][j-1]+dp[i-1][j];}else{dp[i][j]=dp[i-1][j];}}}return dp[s.length()][t.length()];}

相关文章:

【算法刷题 | 动态规划14】6.28(最大子数组和、判断子序列、不同的子序列)
文章目录 35.最大子数组和35.1题目35.2解法:动规35.2.1动规思路35.2.2代码实现 36.判断子序列36.1题目36.2解法:动规36.2.1动规思路36.2.2代码实现 37.不同的子序列37.1题目37.2解法:动规37.2.1动规思路37.2.2代码实现 35.最大子数组和 35.1…...
vue3 vxe-grid列中绑定vxe-switch实现数据更新
1、先上一张图: <template #valueSlot"{ row }"><vxe-switch :value"getV(row.svalue)" change"changeSwitch(row)" /></template>function getV(value){return value 1;};function changeSwitch(row) {console.l…...

Hive SQL:实现炸列(列转行)以及逆操作(行转列)
目录 列转行行转列 列转行 函数: EXPLODE(ARRAY):将ARRAY中的每一元素转换为每一行 EXPLODE(MAP):将MAP中的每个键值对转换为两行,其中一行数据包含键,另一行数据包含值 数据样例: 1、将每天的课程&#…...

MD5算法详解
哈希函数 是一种将任意输入长度转变为固定输出长度的函数。 一些常见哈希函数有:MD5、SHA1、SHA256。 MD5算法 MD5算法是一种消息摘要算法,用于消息认证。 数据存储方式:小段存储。 数据填充 首先对我们明文数据进行处理,使其…...

ES6的代理模式-Proxy
语法 target 要使用 Proxy 包装的目标对象(可以是任何类型的对象,包括原生数组,函数,甚至另一个代理handler 一个通常以函数作为属性的对象,用来定制拦截行为 const proxy new Proxy(target, handle)举个例子 <s…...

排序(堆排序、快速排序、归并排序)-->深度剖析(二)
前言 前面介绍了冒泡排序、选择排序、插入排序、希尔排序,作为排序中经常用到了算法,还有堆排序、快速排序、归并排序 堆排序(HeaSort) 堆排序的概念 堆排序是一种有效的排序算法,它利用了完全二叉树的特性。在C语言…...

七一建党节|热烈庆祝中国共产党成立103周年!
时光荏苒,岁月如梭。 在这热情似火的夏日, 我们迎来了中国共产党成立103周年的重要时刻。 这是一个值得全体中华儿女共同铭记和庆祝的日子, 也是激励我们不断前进的重要时刻。 103年, 风雨兼程,砥砺前行。 从嘉兴…...

Spring Boot应用知识梳理
一.简介 Spring Boot 是一个用于快速开发基于 Spring 框架的应用程序的工具。它简化了基于 Spring 的应用程序的配置和部署过程,提供了一种快速、便捷的方式来构建独立的、生产级别的 Spring 应用程序。 Spring Boot 的一些主要优点包括: 1. 简化配置…...

Spring中利用重载与静态分派
Spring中利用重载与静态分派 在Java和Spring框架中,重载(Overloading)和静态分派(Static Dispatch)是两个非常重要的概念,它们在处理类方法选择和执行过程中扮演着关键角色。本文旨在深入探讨Spring环境下…...

文本三剑客之awk:
文本三剑客awk: grep 查 sed 增删改查 主要:增改 awk 按行取列 awk awk默认的分隔符:空格,tab键,多个空格自动压缩为一个。 awk的工作原理:根据指令信息,逐行的读取文本内容,然…...

SpringSecurity-授权示例
用户基于权限进行授权 定义用户与权限 authorities()。 package com.cms.config;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.security.core.userdetails.User; import…...

选哪个短剧系统源码好:全面评估与决策指南
在短剧内容创作和分享日益流行的今天,选择合适的短剧系统源码对于构建一个成功的短剧平台至关重要。短剧系统源码不仅关系到平台的稳定性和用户体验,还直接影响到内容创作者和观众的互动质量。本文将提供一份全面的评估指南,帮助您在众多短剧…...

AI时代的软件工程:挑战与改变
人工智能(AI)正以惊人的速度改变着我们的生活和工作方式。作为与AI关系最为密切的领域之一,软件工程正经历着深刻的转变。 1 软件工程的演变 软件工程的起源 软件工程(Software Engineering)是关于如何系统化、规范化地…...

Zuul介绍
Zuul 是 Netflix 开源的一个云平台网络层代理,它主要用于路由、负载均衡、中间件通信和动态路由。Zuul 本质上是一个基于 JVM 的网关,它提供了以下功能: 1.路由:Zuul 允许客户端和服务器之间的所有入站和出站请求通过一个中心化的…...
7-1作业
1.实验目的:完成字符收发 led.h #ifndef __GPIO_H__ #define __GPIO_H__#include "stm32mp1xx_rcc.h" #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_uart.h"//RCC,GPIO,UART初始化 void init();//字符数据发送 void set_tt…...

ElasticSearch安装、配置详细步骤
一、环境及版本介绍 操作系统: Windows 10 软件版本: elasticsearch-7.17.22、kibana-7.17.22、IK-7.17.22 开发环境选择软件版本应提前考虑正式系统环境,否则会产生软件与服务器环境不兼容的问题出现,ElasticSearch与环境支持…...
【Mybatis 与 Spring】事务相关汇总
之前分享的几篇文章可以一起看,形成一个体系 【Mybatis】一级缓存与二级缓存源码分析与自定义二级缓存 【Spring】Spring事务相关源码分析 【Mybatis】Mybatis数据源与事务源码分析 Spring与Mybaitis融合 SpringManagedTransaction: org.mybatis.spri…...
)
Leetcode 2065. 最大化一张图中的路径价值(DFS / 最短路)
Leetcode 2065. 最大化一张图中的路径价值 暴力DFS 容易想到,从0点出发DFS,期间维护已经走过的距离(时间)和途径点的权值之和,若访问到0点则更新答案,若下一步的距离与已走过的距离和超出了maxTime&#…...
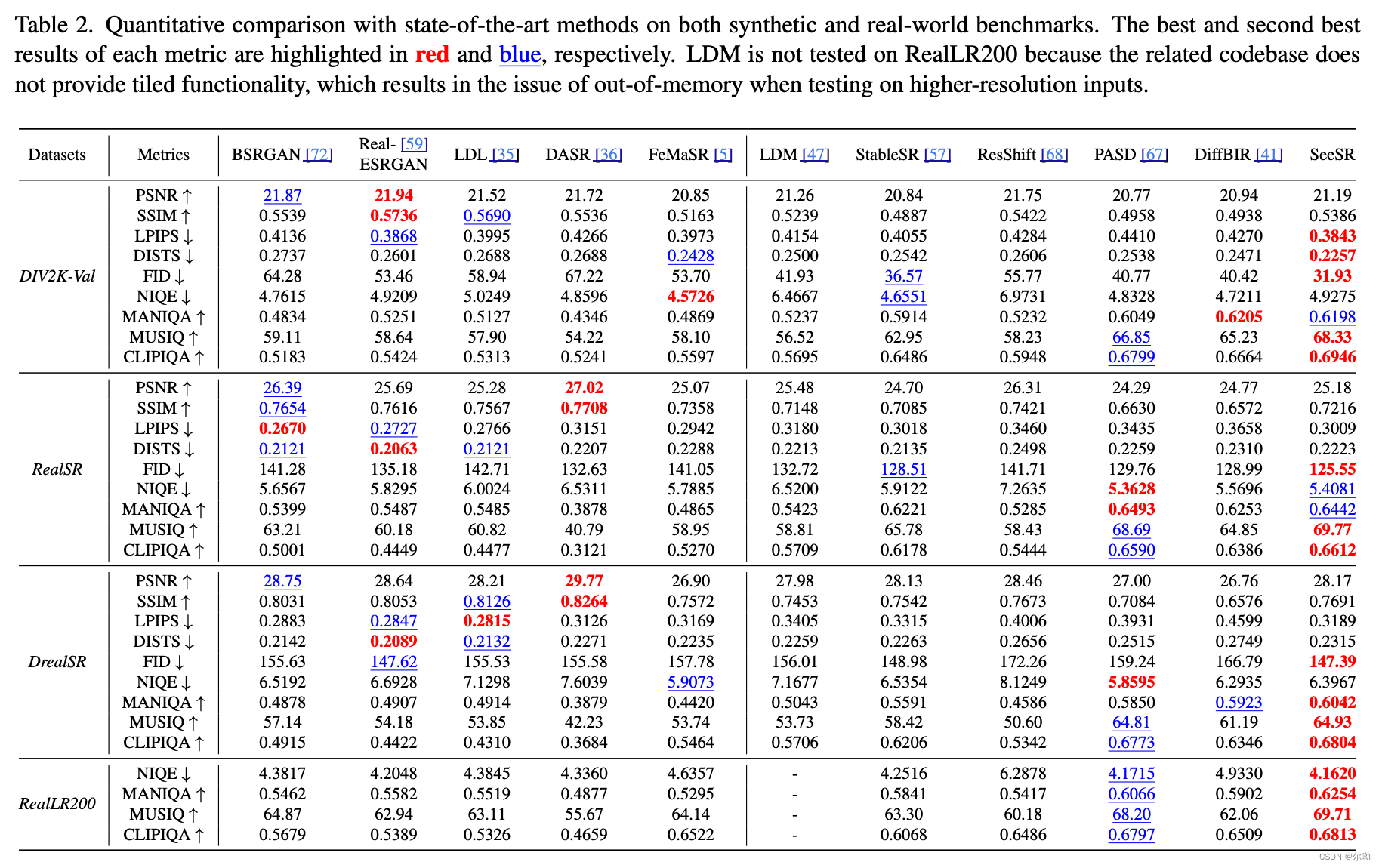
SeeSR: Towards Semantics-Aware Real-World Image Super-Resolution
CVPR2024 香港理工大学&OPPO&bytedancehttps://github.com/cswry/SeeSR?tabreadme-ov-file#-licensehttps://arxiv.org/pdf/2311.16518#page5.80 问题引入 因为有些LR退化情况比较严重,所以超分之后的结果会出现语义的不一致的情况,所以本文训…...
七月论文审稿GPT第5版:拿我司七月的早期paper-7方面review数据集微调LLama 3
前言 llama 3出来后,为了通过paper-review的数据集微调3,有以下各种方式 不用任何框架 工具 技术,直接微调原生的llama 3,毕竟也有8k长度了 效果不期望有多高,纯作为baseline通过PI,把llama 3的8K长度扩展…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
