深入理解二分法
前言
二分法(Binary Search)是一种高效的查找算法,广泛应用于计算机科学和工程领域。它用于在有序数组中查找特定元素,其时间复杂度为 O(log n),显著优于线性搜索的 O(n)。本文将深入介绍二分法的原理、实现及其应用场景,并提供一个详细的C语言实现示例。
二分法的基本思想
二分法通过将搜索空间逐步减半来定位目标值。其基本步骤如下:
- 初始化:定义搜索范围的起始点(left)和终点(right)。
- 查找中点:计算中间位置的索引(mid)。
- 比较中点值:将中点位置的值与目标值进行比较:
- 如果中点值等于目标值,则搜索成功。
- 如果中点值小于目标值,目标值必然位于中点右侧,将左边界更新为 mid + 1。
- 如果中点值大于目标值,目标值必然位于中点左侧,将右边界更新为 mid - 1。
- 重复步骤 2 和 3:直到找到目标值或搜索范围为空。
二分法的实现
以下是一个用C语言编写的二分法实现示例:
#include <stdio.h> // 二分查找函数 int binarySearch(int arr[], int size, int target) { int left = 0; int right = size - 1; while (left <= right) { int mid = left + (right - left) / 2; if (arr[mid] == target) { return mid; // 找到目标值,返回索引 } else if (arr[mid] < target) { left = mid + 1; // 目标值在右半部分 } else { right = mid - 1; // 目标值在左半部分 } } return -1; // 未找到目标值
}
int main() { int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; int size = sizeof(arr) / sizeof(arr[0]); int target = 7; int result = binarySearch(arr, size, target); if (result != -1) { printf("目标值 %d 在数组中的索引为 %d\n", target, result); } else { printf("目标值 %d 不在数组中\n", target); } return 0;
}示例解释
- 定义函数:
binarySearch函数接收三个参数:有序数组arr、数组大小size以及目标值target。 - 初始化:定义左右边界
left和right。 - 计算中点:在循环中计算中点索引
mid。 - 比较并调整边界:根据
arr[mid]与target的比较结果调整left或right。 - 返回结果:找到目标值返回索引,未找到返回 -1。
输出结果
目标值 7 在数组中的索引为 6二分法的应用场景
- 有序数组查找:二分法用于在有序数组中查找特定元素,如在词典中查找单词、数据库索引查找等。
- 二分查找变体:用于查找满足特定条件的最左或最右位置,如在排序数组中查找第一个大于等于某个值的元素。
- 数学求解:二分法可用于求解方程的根,如牛顿迭代法和黄金分割法等。
二分法的优缺点
优点
- 高效性:二分法的时间复杂度为 O(log n),在大数据集上比线性搜索更高效。
- 简单性:二分法算法逻辑简单,易于实现和理解。
缺点
- 有序要求:二分法要求数据是有序的,需先对数据进行排序,这可能会增加额外的时间开销。
- 适用范围:不适用于链表等非连续存储结构,因为无法直接访问中间元素。
总结
二分法是一种高效且广泛应用的搜索算法,适用于有序数据的查找。理解和掌握二分法,对于提升算法效率和解决实际问题具有重要意义。
相关文章:

深入理解二分法
前言 二分法(Binary Search)是一种高效的查找算法,广泛应用于计算机科学和工程领域。它用于在有序数组中查找特定元素,其时间复杂度为 O(log n),显著优于线性搜索的 O(n)。本文将深入介绍二分法的原理、实现及其应用场…...

【C命名规范】遵循良好的命名规范,提高代码的可读性、可维护性和可复用性
/******************************************************************** * brief param return author date version是代码书写的一种规范 * brief :简介,简单介绍函数作用 * param :介绍函数参数 * return:函数返回类型说明 * …...

Hbase面试题总结
一、介绍下HBase架构 --HMaster HBase集群的主节点,负责管理和协调整个集群的操作。它处理元数据和表的分区信息,控制RegionServer的负载均衡和故障恢复。--RegionServer HBase集群中的工作节点,负责存储和处理数据。每个RegionServer管理若…...

C语言部分复习笔记
1. 指针和数组 数组指针 和 指针数组 int* p1[10]; // 指针数组int (*p2)[10]; // 数组指针 因为 [] 的优先级比 * 高,p先和 [] 结合说明p是一个数组,p先和*结合说明p是一个指针 括号保证p先和*结合,说明p是一个指针变量,然后指…...
 : 用override set 设置工具链)
Rust学习笔记 (命令行命令) : 用override set 设置工具链
在cargo run某个项目时出现了如下错误:error: failed to run custom build command for ring v0.16.20(无法运行“Ring v0.16.20”的自定义构建命令),在PowerShell命令行运行命令 rustup override set stable-msvc后成功运行。 o…...

cv::Mat类的矩阵内容输出的各种格式的例子
操作系统:ubuntu22.04OpenCV版本:OpenCV4.9IDE:Visual Studio Code编程语言:C11 功能描述 我们可以这样使用:cv::Mat M(…); cout << M;,直接将矩阵内容输出到控制台。 输出格式支持多种风格,包括O…...

Redis--注册中心集群 Cluster 集群-单服务器
与“多服务器集群”一致需要创建redis配置模板 参照以下链接 CSDN 创建redis容器 node01服务器上创建容器 docker run -d --name redis-6381 --net host --privilegedtrue \ -v /soft/redis-cluster/6381/conf/redis.conf:/etc/redis/redis.conf \ -v /soft/redis-cluster/6…...
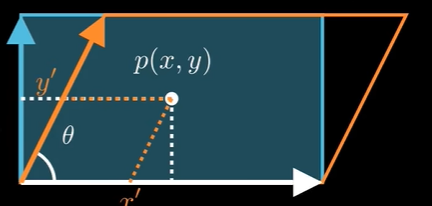
CV01_相机成像原理与坐标系之间的转换
目录 0.引言:小孔成像->映射表达式 1. 相机自身的运动如何表征?->外参矩阵E 1.1 旋转 1.2 平移 2. 如何投影到“像平面”?->内参矩阵K 2.1 图像平面坐标转换为像素坐标系 3. 三维到二维的维度是如何丢失的?…...
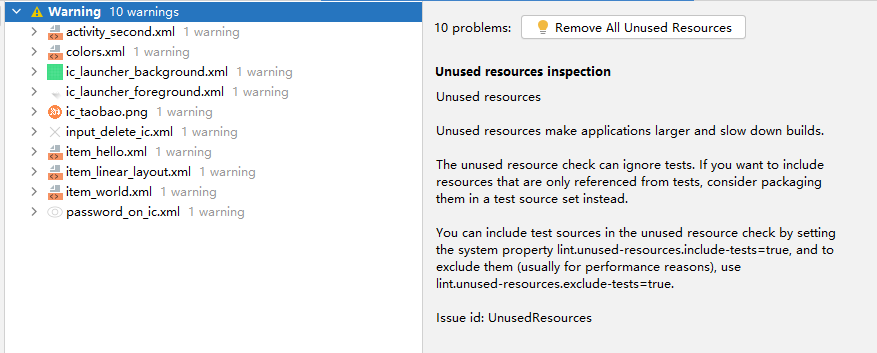
Android Lint
文章目录 Android Lint概述工作流程Lint 问题问题种类警告严重性检查规则 用命令运行 LintAndroidStudio 使用 Lint忽略 Lint 警告gradle 配置 Lint查找无用资源文件 Android Lint 概述 Lint 是 Android 提供的 代码扫描分析工具,它可以帮助我们发现代码结构/质量…...

【算法刷题 | 动态规划14】6.28(最大子数组和、判断子序列、不同的子序列)
文章目录 35.最大子数组和35.1题目35.2解法:动规35.2.1动规思路35.2.2代码实现 36.判断子序列36.1题目36.2解法:动规36.2.1动规思路36.2.2代码实现 37.不同的子序列37.1题目37.2解法:动规37.2.1动规思路37.2.2代码实现 35.最大子数组和 35.1…...
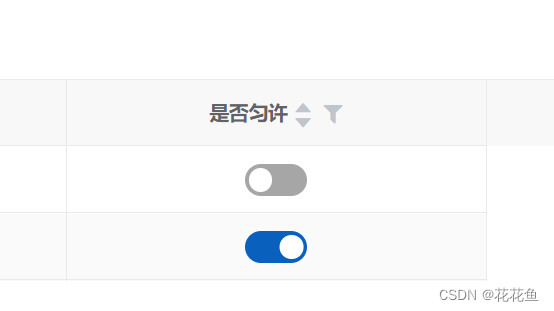
vue3 vxe-grid列中绑定vxe-switch实现数据更新
1、先上一张图: <template #valueSlot"{ row }"><vxe-switch :value"getV(row.svalue)" change"changeSwitch(row)" /></template>function getV(value){return value 1;};function changeSwitch(row) {console.l…...

Hive SQL:实现炸列(列转行)以及逆操作(行转列)
目录 列转行行转列 列转行 函数: EXPLODE(ARRAY):将ARRAY中的每一元素转换为每一行 EXPLODE(MAP):将MAP中的每个键值对转换为两行,其中一行数据包含键,另一行数据包含值 数据样例: 1、将每天的课程&#…...

MD5算法详解
哈希函数 是一种将任意输入长度转变为固定输出长度的函数。 一些常见哈希函数有:MD5、SHA1、SHA256。 MD5算法 MD5算法是一种消息摘要算法,用于消息认证。 数据存储方式:小段存储。 数据填充 首先对我们明文数据进行处理,使其…...

ES6的代理模式-Proxy
语法 target 要使用 Proxy 包装的目标对象(可以是任何类型的对象,包括原生数组,函数,甚至另一个代理handler 一个通常以函数作为属性的对象,用来定制拦截行为 const proxy new Proxy(target, handle)举个例子 <s…...

排序(堆排序、快速排序、归并排序)-->深度剖析(二)
前言 前面介绍了冒泡排序、选择排序、插入排序、希尔排序,作为排序中经常用到了算法,还有堆排序、快速排序、归并排序 堆排序(HeaSort) 堆排序的概念 堆排序是一种有效的排序算法,它利用了完全二叉树的特性。在C语言…...

七一建党节|热烈庆祝中国共产党成立103周年!
时光荏苒,岁月如梭。 在这热情似火的夏日, 我们迎来了中国共产党成立103周年的重要时刻。 这是一个值得全体中华儿女共同铭记和庆祝的日子, 也是激励我们不断前进的重要时刻。 103年, 风雨兼程,砥砺前行。 从嘉兴…...

Spring Boot应用知识梳理
一.简介 Spring Boot 是一个用于快速开发基于 Spring 框架的应用程序的工具。它简化了基于 Spring 的应用程序的配置和部署过程,提供了一种快速、便捷的方式来构建独立的、生产级别的 Spring 应用程序。 Spring Boot 的一些主要优点包括: 1. 简化配置…...

Spring中利用重载与静态分派
Spring中利用重载与静态分派 在Java和Spring框架中,重载(Overloading)和静态分派(Static Dispatch)是两个非常重要的概念,它们在处理类方法选择和执行过程中扮演着关键角色。本文旨在深入探讨Spring环境下…...

文本三剑客之awk:
文本三剑客awk: grep 查 sed 增删改查 主要:增改 awk 按行取列 awk awk默认的分隔符:空格,tab键,多个空格自动压缩为一个。 awk的工作原理:根据指令信息,逐行的读取文本内容,然…...

SpringSecurity-授权示例
用户基于权限进行授权 定义用户与权限 authorities()。 package com.cms.config;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.security.core.userdetails.User; import…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...
