力扣第215题“数组中的第K个最大元素”
在本篇文章中,我们将详细解读力扣第215题“数组中的第K个最大元素”。通过学习本篇文章,读者将掌握如何使用快速选择算法和堆排序来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。
问题描述
力扣第215题“数组中的第K个最大元素”描述如下:
给定整数数组
nums和整数k,请返回数组中第k个最大的元素。你必须设计并实现时间复杂度为
O(n)的算法解决此问题。示例:
输入: [3,2,1,5,6,4], k = 2 输出: 5示例:
输入: [3,2,3,1,2,4,5,5,6], k = 4 输出: 4
解题思路
方法一:快速选择(Quickselect)
-
初步分析:
- 快速选择算法是一种基于快速排序的选择算法,用于在无序列表中查找第 k 小(或大)元素。
- 快速选择通过划分操作将数组分成两部分,一部分大于等于基准元素,另一部分小于基准元素。
-
步骤:
- 使用快速选择算法对数组进行划分,找到第 k 个最大的元素。
- 定义一个辅助函数
partition用于划分数组。 - 根据基准元素的位置,与 k 进行比较,决定递归的方向。
代码实现
def findKthLargest(nums, k):def partition(left, right):pivot = nums[right]p = leftfor i in range(left, right):if nums[i] <= pivot:nums[i], nums[p] = nums[p], nums[i]p += 1nums[p], nums[right] = nums[right], nums[p]return pdef quickselect(left, right, k_smallest):if left == right:return nums[left]pivot_index = partition(left, right)if k_smallest == pivot_index:return nums[k_smallest]elif k_smallest < pivot_index:return quickselect(left, pivot_index - 1, k_smallest)else:return quickselect(pivot_index + 1, right, k_smallest)return quickselect(0, len(nums) - 1, len(nums) - k)# 测试案例
print(findKthLargest([3,2,1,5,6,4], 2)) # 输出: 5
print(findKthLargest([3,2,3,1,2,4,5,5,6], 4)) # 输出: 4
方法二:堆排序
-
初步分析:
- 使用最小堆可以高效地找到第 k 个最大的元素。
- 维护一个大小为 k 的最小堆,堆顶元素即为第 k 个最大的元素。
-
步骤:
- 将数组的前 k 个元素插入最小堆。
- 遍历剩余的元素,如果元素大于堆顶元素,则替换堆顶元素并调整堆。
- 最终,堆顶元素即为第 k 个最大的元素。
代码实现
import heapqdef findKthLargest(nums, k):min_heap = nums[:k]heapq.heapify(min_heap)for num in nums[k:]:if num > min_heap[0]:heapq.heappushpop(min_heap, num)return min_heap[0]# 测试案例
print(findKthLargest([3,2,1,5,6,4], 2)) # 输出: 5
print(findKthLargest([3,2,3,1,2,4,5,5,6], 4)) # 输出: 4
复杂度分析
- 时间复杂度:
- 快速选择(Quickselect):O(n),平均情况下,每次划分会将数组分成两部分。
- 堆排序:O(n log k),维护一个大小为 k 的最小堆。
- 空间复杂度:
- 快速选择(Quickselect):O(1),使用了常数个额外空间。
- 堆排序:O(k),用于存储大小为 k 的最小堆。
模拟面试问答
问题 1:你能描述一下如何解决这个问题的思路吗?
回答:我们可以使用快速选择算法或堆排序来解决这个问题。快速选择算法通过划分数组,找到第 k 个最大的元素。堆排序通过维护一个大小为 k 的最小堆,堆顶元素即为第 k 个最大的元素。
问题 2:为什么选择使用快速选择算法和堆排序来解决这个问题?
回答:快速选择算法是一种高效的选择算法,平均时间复杂度为 O(n)。堆排序通过维护一个最小堆,可以在 O(n log k) 的时间复杂度内找到第 k 个最大的元素。两种方法都可以高效地解决这个问题,适用于处理较大的数据集。
问题 3:你的算法的时间复杂度和空间复杂度是多少?
回答:快速选择算法的时间复杂度为 O(n),空间复杂度为 O(1)。堆排序的时间复杂度为 O(n log k),空间复杂度为 O(k)。
问题 4:在代码中如何处理边界情况?
回答:对于空数组或 k 大于数组长度的情况,可以返回适当的错误信息或值。对于其他情况,通过快速选择或堆排序来处理。
问题 5:你能解释一下快速选择算法的工作原理吗?
回答:快速选择算法通过划分数组,将数组分成两部分,一部分大于等于基准元素,另一部分小于基准元素。根据基准元素的位置,与 k 进行比较,决定递归的方向,最终找到第 k 个最大的元素。
问题 6:在代码中如何确保返回的结果是正确的?
回答:通过快速选择算法或堆排序,找到第 k 个最大的元素,确保返回的结果是正确的。可以通过测试案例验证结果。
问题 7:你能举例说明在面试中如何回答优化问题吗?
回答:在面试中,如果面试官问到如何优化算法,我会首先分析当前算法的瓶颈,如时间复杂度和空间复杂度,然后提出优化方案。例如,可以通过减少不必要的操作和优化数据结构来提高性能。解释其原理和优势,最后提供优化后的代码实现。
问题 8:如何验证代码的正确性?
回答:通过运行代码并查看结果,验证返回的第 k 个最大的元素是否正确。可以使用多组测试数据,包括正常情况和边界情况,确保代码在各种情况下都能正确运行。例如,可以在测试数据中包含多个不同的数组和 k 值,确保代码结果正确。
问题 9:你能解释一下解决数组中的第 K 个最大元素问题的重要性吗?
回答:解决数组中的第 K 个最大元素问题在排序和选择算法中具有重要意义。通过学习和应用快速选择算法和堆排序,可以提高处理排序和选择问题的能力。在实际应用中,第 K 个最大元素问题广泛用于数据分析、统计和优化等领域。
问题 10:在处理大数据集时,算法的性能如何?
回答:算法的性能取决于数据集的大小。在处理大数据集时,通过优化快速选择算法或堆排序的实现,可以显著提高算法的性能。例如,通过减少不必要的操作和优化划分或堆操作,可以减少时间和空间复杂度,从而提高算法的效率。
总结
本文详细解读了力扣第215题“数组中的第K个最大元素”,通过使用快速选择算法和堆排序的方法高效地解决了这一问题,并提供了详细的解释和模拟面试问答。希望读者通过本文的学习,能够在力扣刷题的过程中更加得心应手。
相关文章:

力扣第215题“数组中的第K个最大元素”
在本篇文章中,我们将详细解读力扣第215题“数组中的第K个最大元素”。通过学习本篇文章,读者将掌握如何使用快速选择算法和堆排序来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。…...
java.util.function实现原理和Java使用场景【Function、Predicate集合转换过滤,BiConsumer事件处理】
简介 java.util.function 是 Java 8 引入的一个功能包,它包含了多种函数式接口的定义,使得在 Java 中进行函数式编程变得更为方便。下面我将分别介绍 java.util.function 的作用、实现原理、常用 Java 使用场景以及代码示例。 作用 java.util.function 的主要作用是为 Jav…...

《每天5分钟用Flask搭建一个管理系统》 第6章:数据库集成
第6章:数据库集成 6.1 数据库的选择和配置 在Flask中集成数据库,首先需要选择一个数据库系统。常见的选择包括SQLite、MySQL、PostgreSQL等。选择后,需要配置数据库连接字符串。 示例代码:配置数据库 from flask import Flask…...

pandas读取和处理Excel文件的基础应用1
Pandas如何读取Excel文件并处理数据 引言: Pandas是一种常用的数据处理和分析工具,它提供了丰富的函数和方法,方便用户对数据进行清洗、转换和分析。在实际工作中,我们经常需要处理Excel格式的数据文件,本文将介绍如何…...

electron vite react 创建一个项目
要使用 Electron、Vite 和 React 创建一个项目,你可以按照以下步骤操作: 1. 安装 Node.js 和 npm 首先,确保你的计算机上安装了 Node.js 和 npm(Node Package Manager)。你可以从 Node.js 官网 下载并安装。 2. 初始化一个新的项目 在你的工作目录下,创建一个新的文件…...

鸿蒙使用 @Builder扩展出来的布局数据更新没法更新UI
由于业务的复杂,所以我们把相关UI抽离出来。但是数据变化了,没法更新UI Builder MyGridLayout() { } 通过日志打印发现数据的确是更新了,但是UI就没没办法,如何解决呢 Entry Component struct Page35 {// State sArray: bool…...

湖南省教育网络协会莅临麒麟信安调研教育网络数字化建设及教育信创发展情况
6月28日下午,湖南省教育网络协会理事长张智勇、秘书长刘志勇、副理事长黄旭、胡洪波、周中伟等协会相关负责人一行莅临麒麟信安,就湖南省教育网络数字化建设、教育信创工作等主题进行深入调研。麒麟信安副总裁王攀热情接待。 协会成员一行来到麒麟信安展…...

论文阅读_优化RAG系统的检索
英文名称: The Power of Noise: Redefining Retrieval for RAG Systems 中文名称: 噪声的力量:重新定义RAG系统的检索 链接: https://arxiv.org/pdf/2401.14887.pdf 作者: Florin Cuconasu, Giovanni Trappolini, Federico Siciliano, Simone Filice, Cesare Campag…...
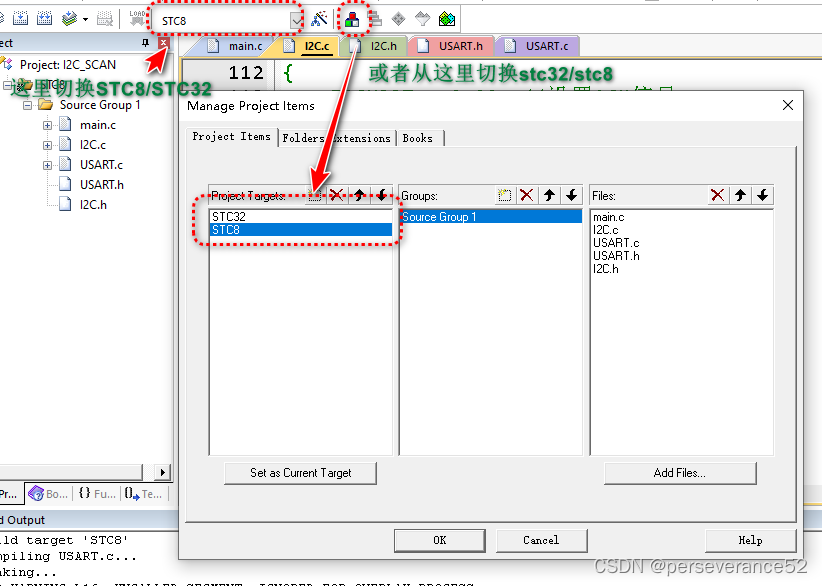
STC8/32 软硬件I2C通讯方式扫描I2C设备地址
STC8/32 软硬件I2C通讯方式扫描I2C设备地址 📄主要用于检测挂载在I2C总线上的设备。在驱动I2C设备之前,如果能扫描到该设备,说明通讯设备可以连接的上,在提前未知I2C地址的情况下,可以方便后面的驱动代码的完善。 🔬扫描测试效果:(测试mpu6050以及ssd1306 i2c oled )…...
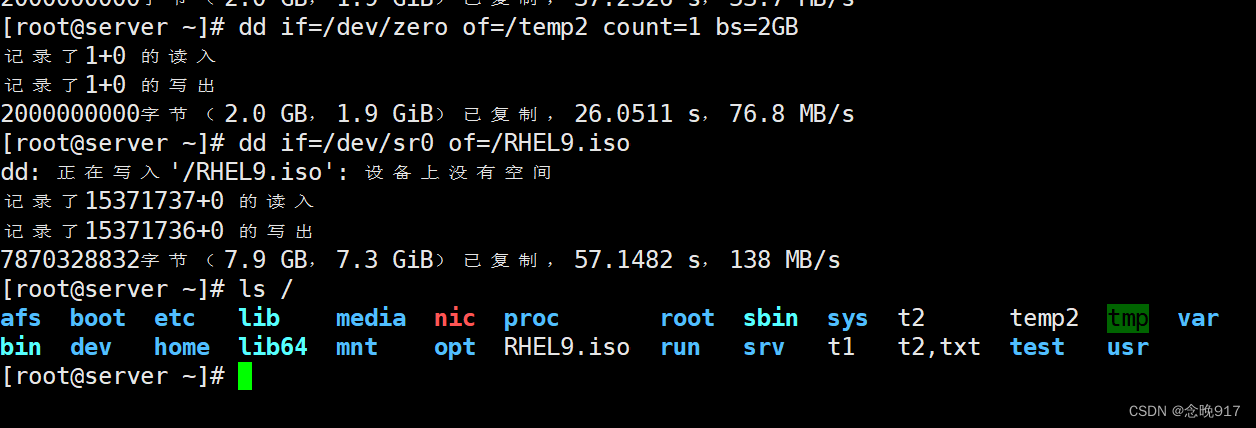
Linux——数据流和重定向,制作镜像
1. 数据流 标准输入( standard input ,简称 stdin ):默认情况下,标准输入指从键盘获取的输入 标准输出( standard output ,简称 stdout ):默认情况下,命令…...

Windows 11的市场份额越来越大了,推荐你升级!
7月1日,系统之家发布最新数据,显示Windows 11操作系统的市场份额正在稳步上升。自2021年10月Windows 11发布以来,Windows 10一直占据着市场主导地位,当时其市场份额高达81.44%。然而,随着时间的推移,Window…...

微服务架构中的调试难题与分布式事务解决方案
微服务架构作为现代软件开发的一种主要趋势,因其灵活性、高可维护性和易于扩展的特点,得到了广泛的应用。然而,在享受微服务架构带来的诸多优点的同时,开发者也面临着一些新的挑战。调试的复杂性和分布式事务的处理是其中两个较为…...

银行家算法-操作系统中避免死锁的最著名算法
背景 有很多文章都会介绍银行家算法。在百度和CSDN上搜一搜能搜出很多来。很多同学会觉得这个算法很深奥,有些文章写的又很复杂,其实真的很简单。这里简单记录一下基本原理,然后大家再配合其他文章看,就能加深理解。 算法原理 …...

PCL 基于点云RGB颜色的区域生长算法
RGB颜色的区域生长算法 一、概述1.1 算法定义1.2 算法特点1.3 算法实现二、代码示例三、运行结果🙋 结果预览 一、概述 1.1 算法定义 点云RGB区域生长算法: 是一个基于RGB颜色信息的区域生长算法,用于点云分割。该算法利用了点云中相邻点之间的颜色相似性来将点云分割成…...

cube-studio开源一站式机器学习平台,在线ide,jupyter,vscode,matlab,rstudio,ssh远程连接,tensorboard
全栈工程师开发手册 (作者:栾鹏) 一站式云原生机器学习平台 前言 开源地址:https://github.com/tencentmusic/cube-studio cube studio 腾讯开源的国内最热门的一站式机器学习mlops/大模型训练平台,支持多租户&…...
1976 ssm 营地管理系统开发mysql数据库web结构java编程计算机网页源码Myeclipse项目
一、源码特点 ssm 营地管理系统是一套完善的信息系统,结合springMVC框架完成本系统,对理解JSP java编程开发语言有帮助系统采用SSM框架(MVC模式开发),系统具有完整的源代码和数据库,系统主要采用B/S模式开…...

技术派全局异常处理
前言 全局的异常处理是Java后端不可或缺的一部分,可以提高代码的健壮性和可维护性。 在我们的开发中,总是难免会碰到一些未经处理的异常,假如没有做全局异常处理,那么我们返回给用户的信息应该是不友好的,很抽象的&am…...

对于mysql 故障的定位和排查
故障表现 他的执行时间超过规定的限制(比如1000ms)CPU使用率高大量业务失败,数据连接异常执行sql越来越慢,失败越来越多 解决方案 定位 应急 故障恢复 定位 查询慢sql的日志查看mysql 的performance schena(里面…...

什么是电航空插头插座连接器有什么作用
航空插头概述 定义与功能 航空插头,又称航空连接器,是一种专门用于航空领域的电连接器,因其最初在航空领域得到广泛应用而得名。航空插头的主要功能是实现电源或信号的连接,尤其适用于芯数较多、结构复杂的线束连接,…...

数据挖掘常见算法(分类算法)
K-近邻算法(KNN) K-近邻分类法的基本思想:通过计算每个训练数据到待分类元组Zu的距离,取和待分类元组距离最近的K个训练数据,K个数据中哪个类别的训练数据占多数,则待分类元组Zu就属于哪个类别…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
