当前位置： 首页 > news >正文

24位DAC转换的FPGA设计及将其封装成自定义IP核的方法

news 2026/2/10 1:08:08

在vivado设计中，为了方便的使用Block Desgin进行设计，可以使用vivado软件把自己编写的代码封装成IP核，封装后的IP核和原来的代码具有相同的功能。本文以实现24位DA转换（含并串转换，使用的数模转换器为CL4660）为例，介绍VIVADO封装IP核的方法及调用方法，以及DAC转换的详细FPGA设计过程，并提供其已验证过的详细代码（使用Verilog语言）。

1 创建IP核

创建一个新的工程，或者打开一个已经存在的工程，点击Tools——Creat and Package New IP...

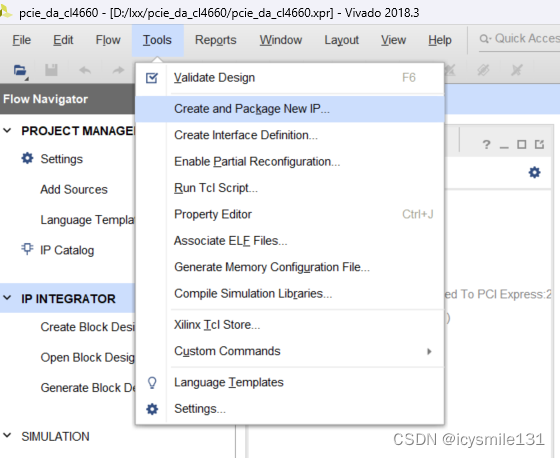
弹出以下对话框，

点击Next，选择Create a new AXI4 peripheral，点击Next，

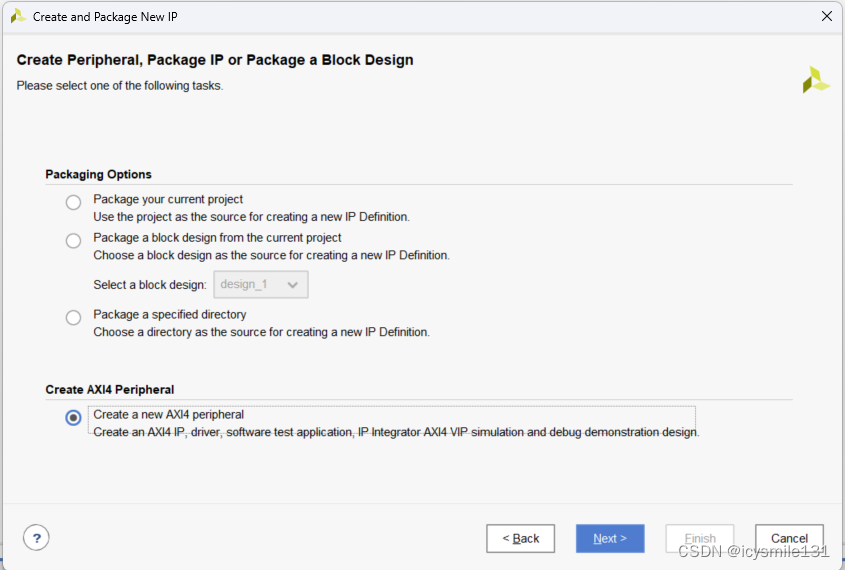
在Name中输入准备生成的IP核的名称，选择Overwrite existing，需要重新生成该IP时，自动覆盖掉原来的设计，

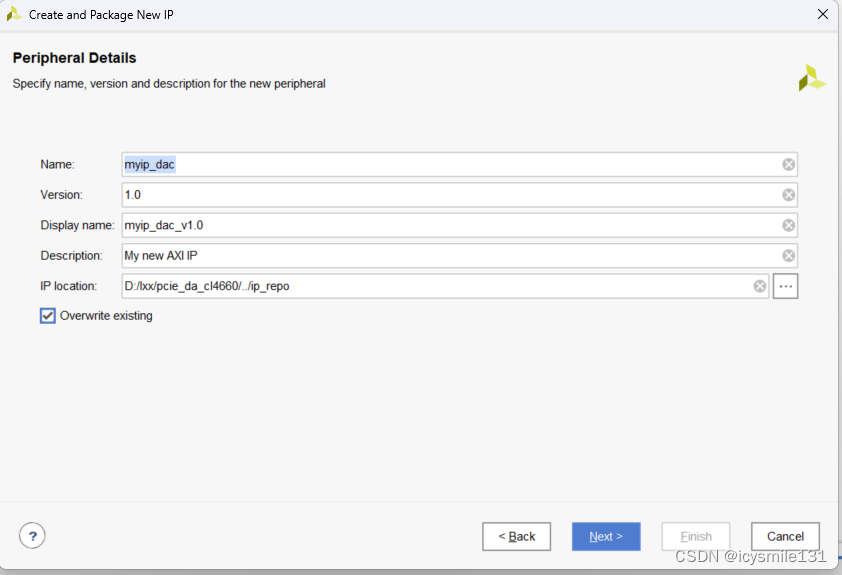
点击Next，Data Width(Bits)为数据宽度，Number of Registers为寄存器的个数，在此需要输入满足设计要求的参数，点击Next，

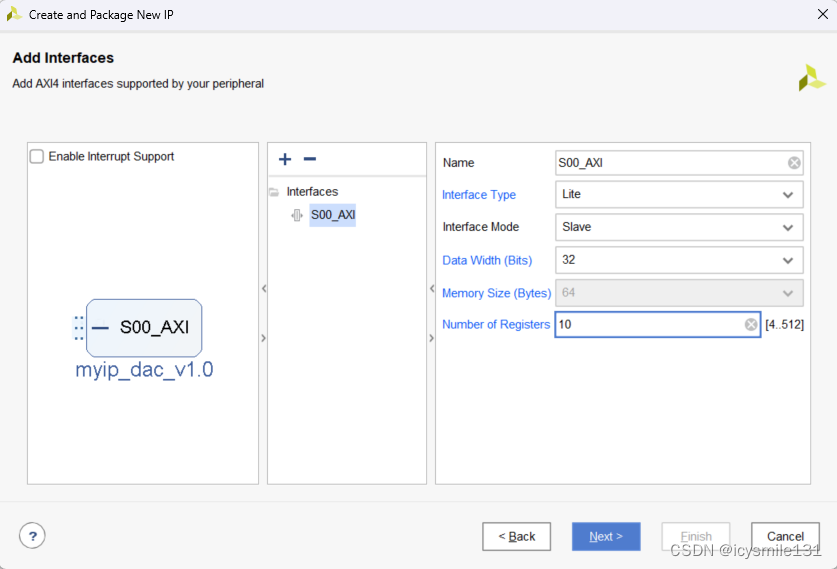
点击Finish，

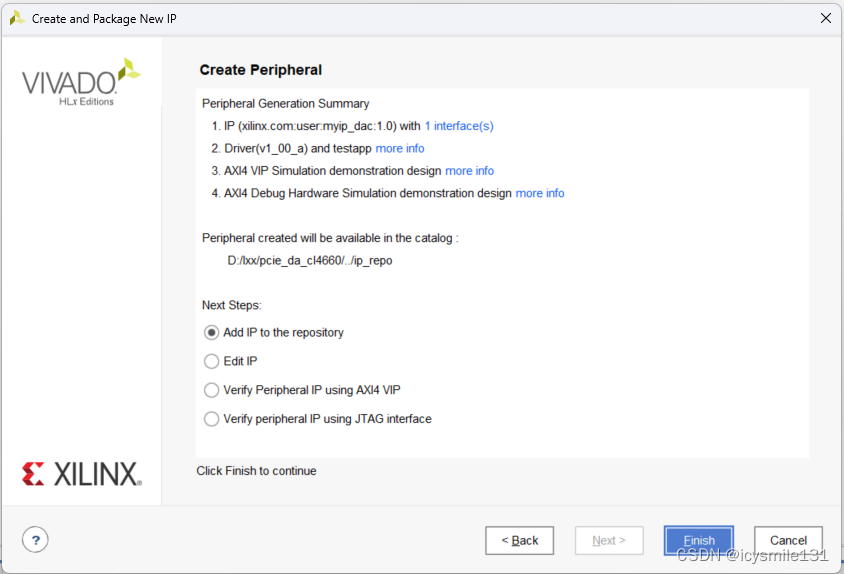
双击PROJECT MANAGER中的IP Catalog，在右侧的IP Catalog中双击新生成的IP核myip_dac_v1.0，

在新弹出的菜单中点击Add IP to Block Design，

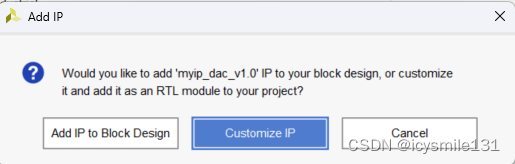
选中myip_dac_v1.0 IP 核，点击右键，在弹出菜单中选择Edit in IP packager，

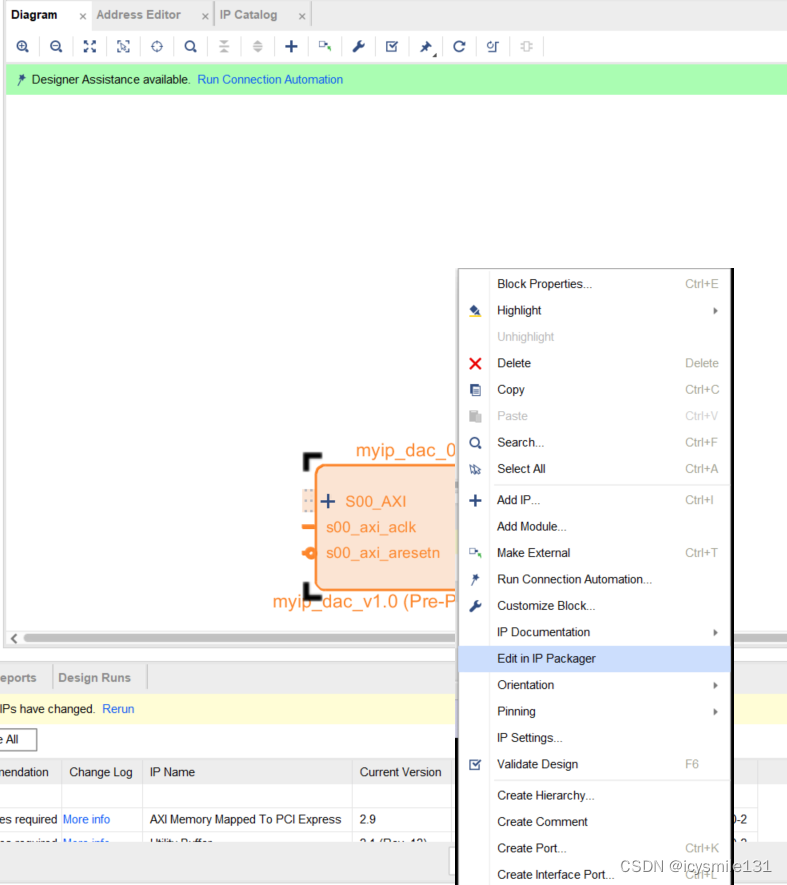
在弹出菜单中选择OK，即可开始编辑新生成的自定义IP核，

相关文章：

24位DAC转换的FPGA设计及将其封装成自定义IP核的方法

在vivado设计中，为了方便的使用Block Desgin进行设计，可以使用vivado软件把自己编写的代码封装成IP核，封装后的IP核和原来的代码具有相同的功能。本文以实现24位DA转换（含并串转换，使用的数模转换器为CL4660）为例，介绍VIVADO封装IP核的方法及调用方法，以及DAC转换的详细…...

编程日记 2024/7/3 21:42:48

【大模型LLM面试合集】大语言模型基础_llm概念

1.llm概念 1.目前 主流的开源模型体系 有哪些？ 目前主流的开源LLM（语言模型）模型体系包括以下几个： GPT（Generative Pre-trained Transformer）系列：由OpenAI发布的一系列基于Transformer架构…...

编程日记 2024/7/3 21:41:47

Qt时间日期处理与定时器使用总结

一、日期时间数据 1.QTime 用于存储和操作时间数据的类，其中包括小时(h)、分钟(m)、秒(s)、毫秒(ms)。函数定义如下： //注：秒(s)和毫秒(ms)有默认值0 QTime::QTime(int h, int m, int s 0, int ms 0) 若无须初始化时间数据，可…...

编程日记 2024/7/3 21:37:40

数据结构——Hash Map

1. Hash Map简介 Hash Map是一种基于键值对的数据结构，通过散列函数将键映射到存储位置，实现快速的数据查找和存储。它可以在常数时间内完成查找、插入和删除操作，因此在需要频繁进行这些操作时非常高效。 2. Hash Map的定义 散列表&#xff…...

编程日记 2024/7/3 21:35:38

剪画小程序：视频剪辑-视频播放倍数的调整与应用

在这个快节奏的时代，时间变得越来越宝贵，而视频倍数播放功能就像是我们的时间管理小助手，为我们的视频观看带来了极大的便利。你是否好奇它到底能在哪些地方发挥作用呢？让我们一起来看看！ 只要使用小程序【剪画】的里…...

编程日记 2024/7/3 21:33:36

使用 Java Swing 和 XChart 创建多种图表

在现代应用程序开发中，数据可视化是一个关键部分。本文将介绍如何使用 Java Swing 和 XChart 库创建各种类型的图表。XChart 是一个轻量级的图表库，支持多种类型的图表，非常适合在 Java 应用中进行快速的图表绘制。 1、环境配置 在开始之前&…...

编程日记 2024/7/3 21:32:34

信息系统运维管理：实践与发展

信息系统运维管理：实践与发展 信息系统运维管理在现代企业中扮演着至关重要的角色，确保信息系统的高效、安全和稳定运行。本文结合《信息系统运维管理》文档内容，探讨了服务设计阶段、服务转换阶段、委托系统维护管理三个主要章节&#xff0…...

编程日记 2024/7/3 21:30:32

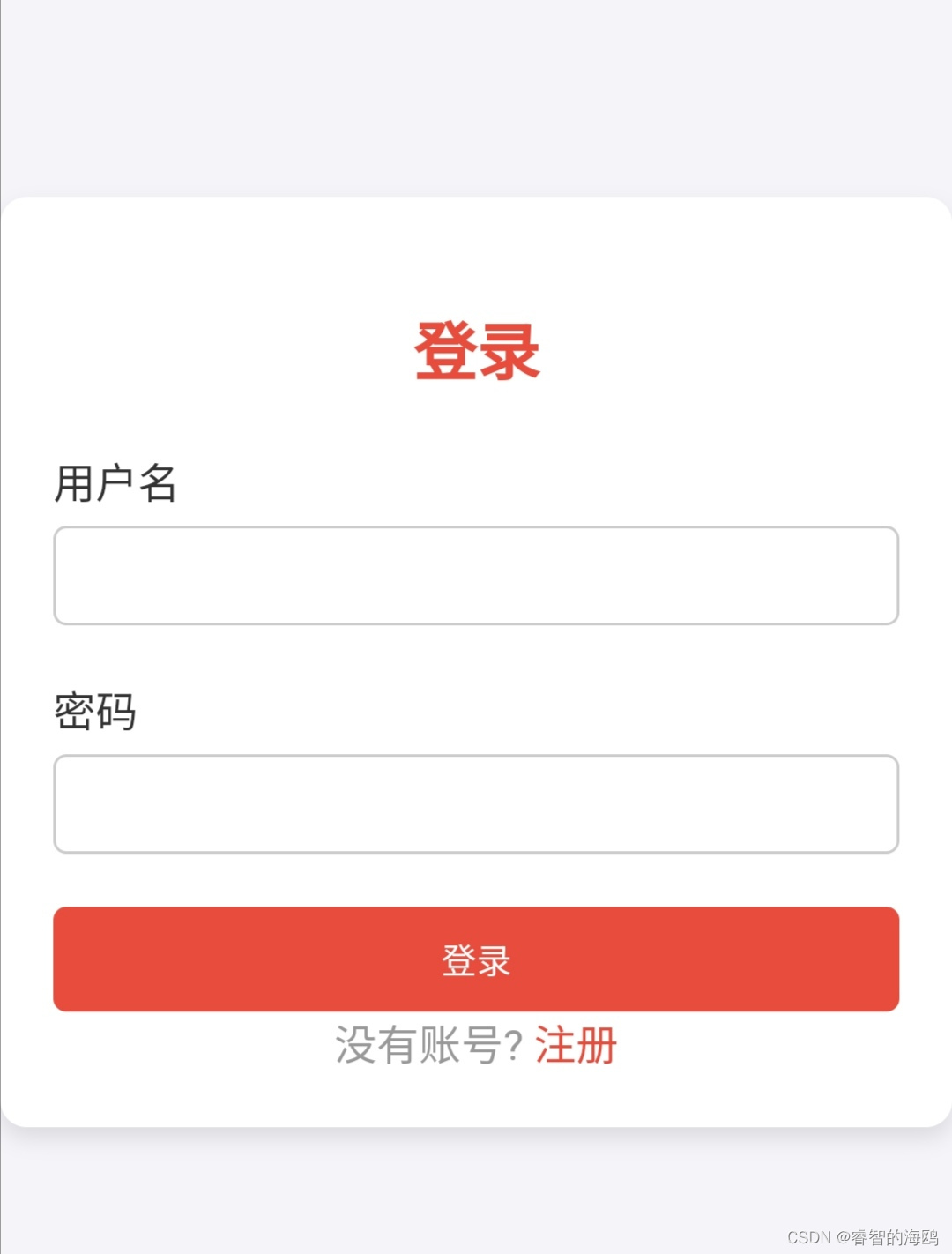
html+js+css登录注册界面

拥有向服务器发送登录或注册数据并接收返回数据的功能 点赞关注 界面 源代码 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <title>Login and Registration Form</title> <style> * …...

编程日记 2024/7/3 21:29:31

英伟达（NVIDIA）数据中心GPU介绍

英伟达&#xff08;NVIDIA&#xff09;数据中心GPU按性能由高到低排行&#xff1a; 1. NVIDIA H100 架构&#xff1a;Hopper 核心数量&#xff1a;18352 CUDA Cores, 1456 Tensor Cores 显存&#xff1a;80 GB HBM3 峰值性能&#xff1a; 单精度&#xff08;FP32&#xff09…...

编程日记 2024/7/3 21:28:30

Leetcode 3202. Find the Maximum Length of Valid Subsequence II

Leetcode 3202. Find the Maximum Length of Valid Subsequence II 1. 解题思路2. 代码实现 题目链接&#xff1a;3202. Find the Maximum Length of Valid Subsequence II 1. 解题思路 这一题的话是上一题3201. Find the Maximum Length of Valid Subsequence I的升级版&am…...

编程日记 2024/7/3 21:27:29

通过Spring Boot结合实时流媒体技术对考试过程进行实时监控

本章将深入探讨考试系统中常见的复杂技术问题&#xff0c;并提供基于Spring Boot 3.x的解决方案。涵盖屏幕切换检测与防护、接打电话识别处理、行为监控摄像头使用、网络不稳定应对等&#xff0c;每篇文章详细剖析问题并提供实际案例与代码示例&#xff0c;帮助开发者应对挑战&…...

编程日记 2024/7/3 21:26:28

智能扫地机器人避障与防跌落问题解决方案

智能扫地机器人出现避障与防跌落问题时&#xff0c;可以通过以下几种方式来解决&#xff1a; 一、避障问题的解决方案 1.升级避障技术&#xff1a; ①　激光雷达避障&#xff1a;激光雷达通过发射和接收激光信号来判断与障碍物的距离&#xff0c;具有延迟低、效果稳定、准确度…...

编程日记 2024/7/3 21:22:24

德旺训练营称重问题

这是考小学的分治策略&#xff0c;小学的分治策略几乎都是分三组。本着这个策略&#xff0c;我们做看看。 第一次称重&#xff1a; 分三组&#xff0c;16,16,17&#xff0c;拿两个16称&#xff0c;得到A情况&#xff0c;一样重&#xff0c;那么假铜钱在那组17个里面。B情况不…...

编程日记 2024/7/3 21:21:23

数据决策系统详解

文章目录 数据决策系统的核心组成部分&#xff1a;1. **数据收集与整合**&#xff1a;2. **数据处理与分析**&#xff1a;3. **数据可视化**&#xff1a;4. **决策支持**&#xff1a; 数据决策系统的功能&#xff1a;决策类型&#xff1a;数据决策系统对企业的重要性&#xff1…...

编程日记 2024/7/3 21:20:22

JSON 简述与应用

1. JSON 简述 JSON&#xff08;JavaScript Object Notation&#xff09;是一种轻量级的数据交换格式&#xff0c;常用于客户端与服务器之间的数据传递。它基于JavaScript对象表示法&#xff0c;但独立于语言&#xff0c;可以被多种编程语言解析和生成。 1.1 特点 轻量级&#…...

编程日记 2024/7/3 21:18:20

ResNet50V2

&#x1f368; 本文为&#x1f517;365天深度学习训练营 中的学习记录博客&#x1f356; 原作者&#xff1a;K同学啊 一、ResNetV1和ResNetV2的区别 ResNetV2 和 ResNetV1 都是深度残差网络&#xff08;ResNet&#xff09;的变体&#xff0c;它们的主要区别在于残差块的设计和…...

编程日记 2024/7/3 21:15:18

基于深度学习的虚拟换装

基于深度学习的虚拟换装技术旨在通过计算机视觉和图像处理技术&#xff0c;将不同的服装虚拟地穿在用户身上&#xff0c;实现快速的试穿和展示。这项技术在电商、时尚和虚拟现实领域具有广泛的应用&#xff0c;能够提升用户体验&#xff0c;增加互动性。以下是关于这一领域的系…...

编程日记 2024/7/3 21:14:17

单段时间最优S型速度规划算法

一&#xff0c;背景 在做机械臂轨迹规划的单段路径的速度规划时&#xff0c;除了参考《Trajectory Planning for Automatic Machines and Robots》等文献之外&#xff0c;还在知乎找到了这位大佬 韩冰 写的在线规划方法&#xff1a; https://zhuanlan.zhihu.com/p/585253101/e…...

编程日记 2024/7/3 21:12:15

pom文件-微服务项目结构

一、微服务项目结构 my-microservices-project/ ├── pom.xml <!-- 父模块的pom.xml --> ├── ry-system/ │ ├── pom.xml <!-- 子模块ry-system的pom.xml --> │ └── src/main/java/com/example/rysystem/ │ └── RySystemApplication.…...

编程日记 2024/7/3 21:11:14

解析Kotlin中的Nothing【笔记摘要】

1.Nothing的本质 Nothing 的源码很简单&#xff1a; public class Nothing private constructor()可以看到它是个class&#xff0c;但它的构造函数是 private 的&#xff0c;这就导致我们没法创建它的实例&#xff0c;并且在源码里 Kotlin 也没有帮我们创建它的实例。 基于这…...

编程日记 2024/7/3 21:10:13

业务系统对接大模型的基础方案：架构设计与关键步骤

业务系统对接大模型&#xff1a;架构设计与关键步骤 在当今数字化转型的浪潮中&#xff0c;大语言模型&#xff08;LLM&#xff09;已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中&#xff0c;不仅可以优化用户体验&#xff0c;还能为业务决策提供…...

编程新知 2026/2/8 4:53:03

零门槛NAS搭建：WinNAS如何让普通电脑秒变私有云？

一、核心优势&#xff1a;专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发&#xff0c;是一款收费低廉但功能全面的Windows NAS工具&#xff0c;主打“无学习成本部署” 。与其他NAS软件相比&#xff0c;其优势在于&#xff1a; 无需硬件改造&#xff1a;将任意W…...

编程新知 2026/1/2 23:01:24

图表类系列各种样式PPT模版分享

图标图表系列PPT模版&#xff0c;柱状图PPT模版&#xff0c;线状图PPT模版&#xff0c;折线图PPT模版&#xff0c;饼状图PPT模版&#xff0c;雷达图PPT模版&#xff0c;树状图PPT模版 图表类系列各种样式PPT模版分享&#xff1a;图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

编程新知 2026/2/4 18:07:02

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用

中达瑞和自2005年成立以来&#xff0c;一直在光谱成像领域深度钻研和发展&#xff0c;始终致力于研发高性能、高可靠性的光谱成像相机&#xff0c;为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

编程新知 2025/12/31 17:08:10

Python实现简单音频数据压缩与解压算法

Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中&#xff0c;压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言&#xff0c;提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

编程新知 2025/9/18 22:43:13

【iOS】 Block再学习

iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

编程新知 2026/2/1 20:22:45

CTF show 数学不及格

拿到题目先查一下壳&#xff0c;看一下信息 发现是一个ELF文件&#xff0c;64位的 ​ 用IDA Pro 64 打开这个文件 ​ 然后点击F5进行伪代码转换 可以看到有五个if判断&#xff0c;第一个argc ! 5这个判断并没有起太大作用&#xff0c;主要是下面四个if判断 ​ 根据题目…...

编程新知 2026/2/8 17:00:05

【Ftrace 专栏】Ftrace 参考博文

ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

编程新知 2026/1/20 3:30:27

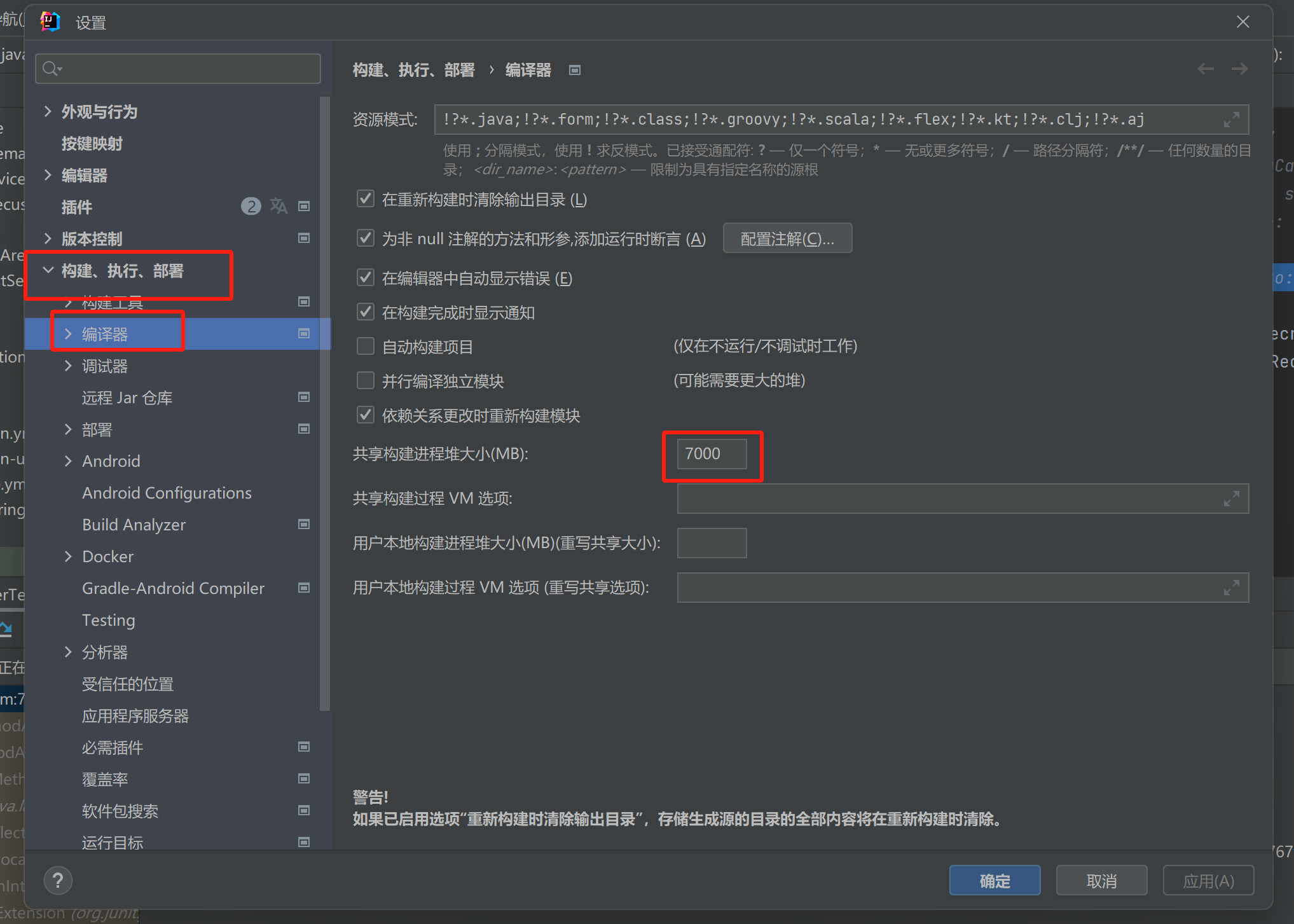
【记录坑点问题】IDEA运行：maven-resources-production:XX: OOM: Java heap space

问题&#xff1a;IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案&#xff1a;将编译的堆内存增加一点 位置&#xff1a;设置setting-》构建菜单build-》编译器Complier...

编程新知 2026/1/26 19:41:09

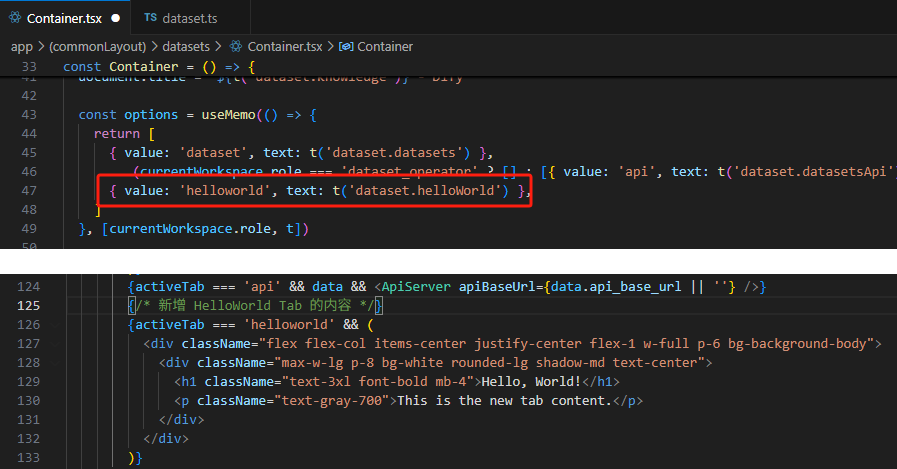
【技巧】dify前端源代码修改第一弹-增加tab页

回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码&#xff0c;在知识库增加一个tab页"HELLO WORLD"&#xff0c;完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

编程新知 2026/2/8 9:41:45