DP:背包问题----0/1背包问题
文章目录
- 💗背包问题
- 💛背包问题的变体
- 🧡0/1 背包问题的数学定义
- 💚解决背包问题的方法
- 💙例子
- 💗解决背包问题的一般步骤?
- 💗例题
- 💗总结

❤️❤️❤️❤️❤️博客主页:lyyyyrics❤️❤️❤️❤️❤️

💗背包问题
背包问题(Knapsack Problem)是一类经典的组合优化问题,在计算机科学和数学中有广泛应用。其基本问题是:
- 输入:给定一个容量为 W W W 的背包和 n n n 个物品,每个物品 i i i 有一个重量 w i w_i wi 和一个价值 v i v_i vi。
- 目标:选择若干个物品放入背包,使得总重量不超过背包的容量 W W W,并且总价值最大化。
💛背包问题的变体
- 0/1 背包问题:每个物品只能选择一次,即要么选中(1)要么不选(0)。
- 分数背包问题:每个物品可以分割,即可以选择物品的一部分。
- 多重背包问题:每个物品有多个副本,可以选择多个相同的物品。
- 多维背包问题:背包有多个限制条件,例如容量和体积等。
🧡0/1 背包问题的数学定义
目标函数:
maximize ∑ i = 1 n c i ⋅ x i \text{maximize} \sum_{i=1}^{n} c_i \cdot x_i maximizei=1∑nci⋅xi
其中, n n n 表示物品的数量, c i c_i ci 表示物品 i i i 的价值。
约束条件:
∑ i = 1 n w i ⋅ x i ≤ C \sum_{i=1}^{n} w_i \cdot x_i \leq C i=1∑nwi⋅xi≤C
其中, w i w_i wi 表示物品 i i i 的重量, C C C 表示背包的容量。
其它约束条件:
x i ∈ { 0 , 1 } x_i \in \{0,1\} xi∈{0,1}
i = 1 , 2 , 3 , … , n i = 1,2,3,\ldots,n i=1,2,3,…,n
其中, x i x_i xi 表示物品 i i i 是否被选中。
💚解决背包问题的方法
解决背包问题的方法有很多,包括动态规划、分支定界法、贪心算法(适用于分数背包问题)以及各种近似算法和启发式算法等。
💙例子
假设有一个背包容量为 50 的背包,有以下物品:
| 物品 | 重量 | 价值 |
|---|---|---|
| 1 | 10 | 60 |
| 2 | 20 | 100 |
| 3 | 30 | 120 |
目标是选择物品使得总重量不超过 50 且总价值最大化。在这个例子中,最佳选择是选取物品 2 和物品 3,总重量为 50,总价值为 220。
💗解决背包问题的一般步骤?
背包问题是一个经典的优化问题,可以通过动态规划算法来解决。下面是解决背包问题的一般步骤:
-
确定问题的约束条件:背包的容量限制和物品的重量和价值。
-
定义状态:将问题拆解为多个子问题,定义状态为背包的容量和可选择的物品。
-
定义状态转移方程:根据子问题的定义,确定状态之间的关系。例如,对于背包问题,可以定义状态转移方程为f(i,j),表示在前i个物品中选择,背包容量为j时,可以获得的最大价值。则可以得到状态转移方程:f(i,j) = max(f(i-1,j), f(i-1,j-w[i])+v[i]),其中w[i]和v[i]分别表示第i个物品的重量和价值。
-
确定初始条件:确定边界条件,即背包容量为0时,价值为0。
-
通过动态规划算法计算最优解:根据状态转移方程和初始条件,利用循环或递归的方式计算最优解。
-
回溯最优解:根据计算得到的最优解,可以通过回溯的方式确定选择了哪些物品放入背包中,从而得到最终的解。
需要注意的是,背包问题的解决方法还包括贪心算法、分支界限算法等。具体选择哪种方法取决于问题的约束条件和需要优化的目标。
💗例题
题目链接
题目:
样例输出和输入:
这道题并不是leetcode的那种接口的模式,而是ACM模式,我们需要进行完整的输入和输出,我们先分析第一个样例:
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| 容量 | 2 | 4 | 1 |
| 价值 | 10 | 5 | 4 |
第一个问题是给定一个背包容量,求出当背包的容量不用装满时的最大价值,意思就是我们选出的物品的总的容量可以小于背包的容量,也可以等于背包的容量,这时,我们可以第一个物品和三个物品的价值是最大的。
总价值为14,
第二个问题是我们必须将 背包容量给塞满,求塞满的状态的物品的最大价值,这种情况下有可能是没有结果的,因为无法选出能将背包塞满的组合 ,所以这时候就输出零。但是这个例子是可以输出结果的,塞满的情况应该是第二个物品和第三个物品,总价值是9,所以最后输出14和9。
算法原理:
状态表示:dp[i][j]-----表示选到第i个位置时的所有选法中的不超过总容积j的最大价值。
状态转移方程:
这是不把背包填满的情况下的状态转移方程,还有一个问题就是需要将背包填满。
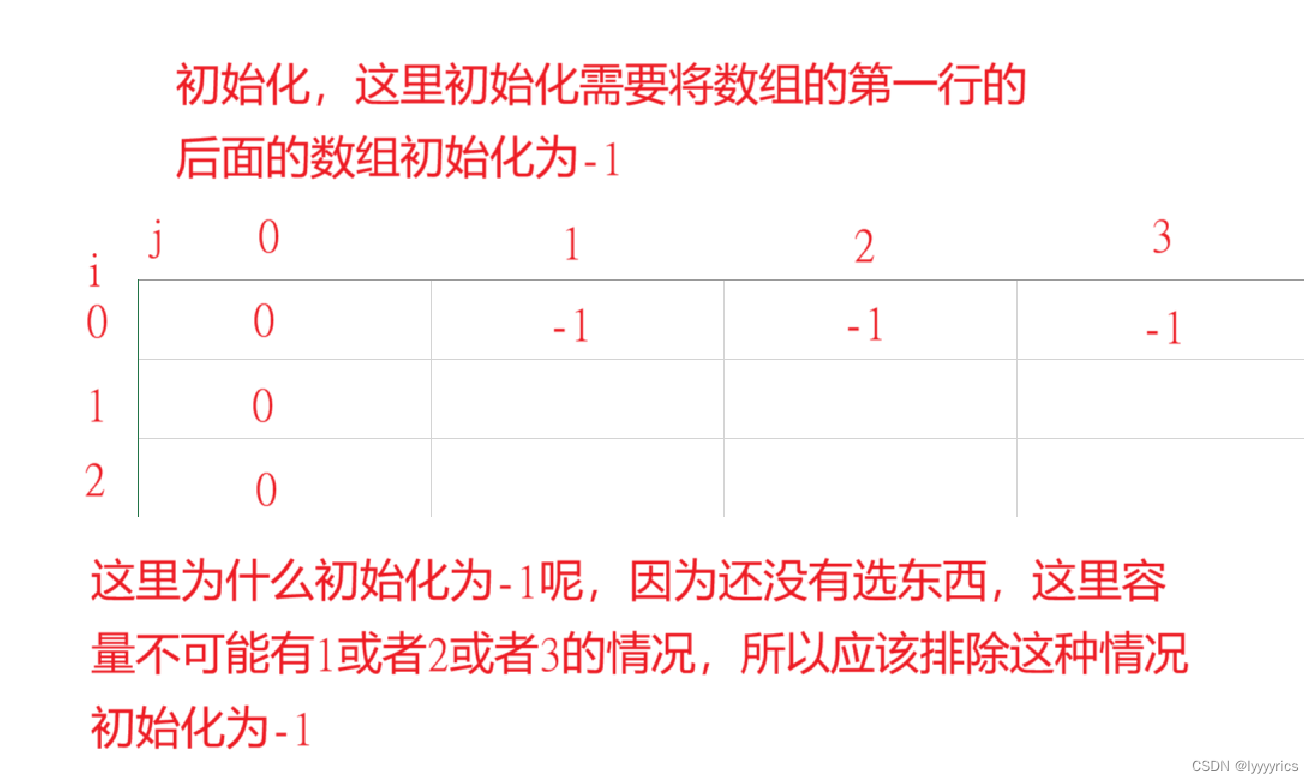
所以这里如果要用到前一个状态的话,应该判断一下前一个状态是否是-1,如果前一个状态是-1的话,就表示这种情况根本不存在 ,所以不能选择这种状态
初始化:第一个问题的初始化只需要将dp表初始化为0,第二个问题的初始化上面已经讨论过了。
填表顺序:也是按照从左上角到右下角,依次填表。
返回值:返回dp[n][V]
代码展示:
#include <cstring>
#include <iostream>
#include<string>
using namespace std;//数据范围
const int N = 1010;
//n个数据,V为背包的总容量,v表示单个物品的所占容积,w表示单个物品所含的价值
int n, V, v[N], w[N];
//i表示第i个位置,j表示总的容积
int dp[N][N];int main()
{//输入总数据,和总容积cin >> n >> V;for (int i = 1;i <= n;i++){cin >> v[i] >> w[i];}//解决第一问for (int i = 1;i <= n;i++){//j表示容量for (int j = 1;j <= V;j++){//不选的情况dp[i][j] = dp[i - 1][j];//如果能选,则和之前不选的情况求一个maxif (j >= v[i])dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}//输出最后一个dp状态cout << dp[n][V] << endl;//重置dp表,将表中数据重置为0memset(dp, 0, sizeof dp);//单独初始化第一排的后面的位置,因为如果没有任何物品根本不可能有价值,所以初始化为-1for (int i = 1;i <= V;i++){//初始化不存在dp的位置dp[0][i] = -1;}for (int i = 1;i <= n;i++){//j表示容量for (int j = 1;j <= V;j++){//可以不选dp[i][j] = dp[i - 1][j];//如果要选择当前位置的话需要考虑前一个状态是否是-1,选不到的情况 if (j >= v[i] && dp[i - 1][j - v[i]] != -1)dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}//如果不存在选满的情况,直接返回0,否则返回dp[n][V]位置的值cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}
代码优化:
可以利用滚动数组进行优化:
#include <cstring>
#include <iostream>
#include<string>
using namespace std;//数据范围
const int N = 1010;
//n个数据,V为背包的总容量,v表示单个物品的所占容积,w表示单个物品所含的价值
int n, V, v[N], w[N];
//i表示第i个位置,j表示总的容积
int dp[N];int main()
{//输入总数据,和总容积cin >> n >> V;for (int i = 1;i <= n;i++)cin >> v[i] >> w[i];//解决第一问for (int i = 1;i <= n;i++)//j表示容量for (int j = V;j >= v[i];j--)//修改遍历顺序//如果能选,则和之前不选的情况求一个maxdp[j] = max(dp[j], dp[j - v[i]] + w[i]);//输出最后一个dp状态cout << dp[V] << endl;//重置dp表,将表中数据重置为0memset(dp, 0, sizeof dp);//单独初始化第一排的后面的位置,因为如果没有任何物品根本不可能有价值,所以初始化为-1for (int i = 1;i <= V;i++)//初始化不存在dp的位置dp[i] = -1;for (int i = 1;i <= n;i++)//j表示容量for (int j = V;j >= v[i];j--)//修改遍历顺序//如果能选,则和之前不选的情况求一个maxif(dp[j-v[i]]!=-1)dp[j] = max(dp[j], dp[j - v[i]] + w[i]);//如果不存在选满的情况,直接返回0,否则返回dp[n][V]位置的值cout << (dp[V] == -1 ? 0 : dp[V]) << endl;return 0;
}
运行结果:

💗总结
通过对0/1背包问题的分析和动态规划解法的详细讲解,我们可以看到这种经典问题在算法设计中的重要性。0/1背包问题不仅是许多实际应用的基础,也是理解和掌握动态规划思想的一个重要实例。
在解决0/1背包问题时,关键在于构建状态转移方程并合理使用空间和时间资源。通过递归和迭代的方法,我们能更好地理解背包问题的解法,优化算法效率,并提升解决复杂问题的能力。
希望这篇博客能帮助你理解0/1背包问题的基本原理和解法,同时激发你对动态规划和算法设计的进一步兴趣和探索。未来的学习中,不妨尝试更多的变种背包问题和动态规划问题,以不断提升自己的算法技能和编程水平。
相关文章:

DP:背包问题----0/1背包问题
文章目录 💗背包问题💛背包问题的变体🧡0/1 背包问题的数学定义💚解决背包问题的方法💙例子 💗解决背包问题的一般步骤?💗例题💗总结 ❤️❤️❤️❤️❤️博客主页&…...

React antd umi 监听当前页面离开,在菜单栏提示操作
需求是我这里有个页面,离开当前页面之后,需要在菜单栏显示个提示,也就是Tour const [unblock, setUnblock] useState<() > void>(() > () > {});const [next, setNext] useState();useEffect(() > {const unblockHandler…...

在 Windows PowerShell 中模拟 Unix/Linux 的 touch 命令
在 Unix 或 Linux 系统中,touch 命令被广泛用于创建新文件或更新现有文件的时间戳。不过,在 Windows 系统中,尤其是在 PowerShell 环境下,并没有内置的 touch 命令。这篇博客将指导你如何在 Windows PowerShell 中模拟 touch 命令…...

鸿蒙NEXT
[中国,东莞,2024年6月24日] 华为开发者大会(HDC)正式开幕,带来全新的 HarmonyOS NEXT、盘古大模型5.0等最创新成果,持续为消费者和开发者带来创新体验。 HarmonyOS NEXT 鸿蒙生态 星河璀璨 鸿蒙生态设备数…...

VUE3-Elementplus-form表单-笔记
1. 结构相关 el-row表示一行,一行分成24份 el-col表示列 (1) :span"12" 代表在一行中,占12份 (50%) (2) :span"6" 表示在一行中,占6份 (25%) (3) :offset"3" 代表在一行中,左侧margin份数 el…...
Analyze an ORA-12801分析并行 parallel 12801 实际原因
"ORA-06512: at "PKG_P_DATA", line 19639 ORA-06512: at "PKG_P_DATA", line 19595 ORA-06512: at "PKG_P_DATA", line 14471-JOB 调用 -ORA-12801: error signaled in parallel query server P009, instance rac2:dwh2 (2) Error: ORA-12…...
高级运维工程师讲述银河麒麟V10SP1服务器加固收回权限/tmp命令引起生产mysql数据库事故实战
高级运维工程师讲述银河麒麟V10SP1服务器加固收回权限/tmp命令引起生产MySql数据库事故实战 一、前言 作为运维工程师经常会对生产服务器进行安全漏洞加固,一般服务厂商、或者甲方信息安全中心提供一些安全的shell脚本,一般这种shell脚本都是收回权限&…...

昇思25天学习打卡营第09天|sea_fish
打开第九天,本次学习的内容为保存与加载,记录学习的过程。本次的内容少而且简单。 在训练网络模型的过程中,实际上我们希望保存中间和最后的结果,用于微调(fine-tune)和后续的模型推理与部署,因…...
flutter开发实战-Charles抓包设置,dio网络代理
flutter开发实战-Charles抓包设置 在开发过程中抓包,可以看到请求参数等数据,方便分析问题。flutter上使用Charles抓包设置。dio需要设置网络代理。 一、dio设置网络代理 在调试模式下需要抓包调试,所以需要使用代理,并且仅用H…...
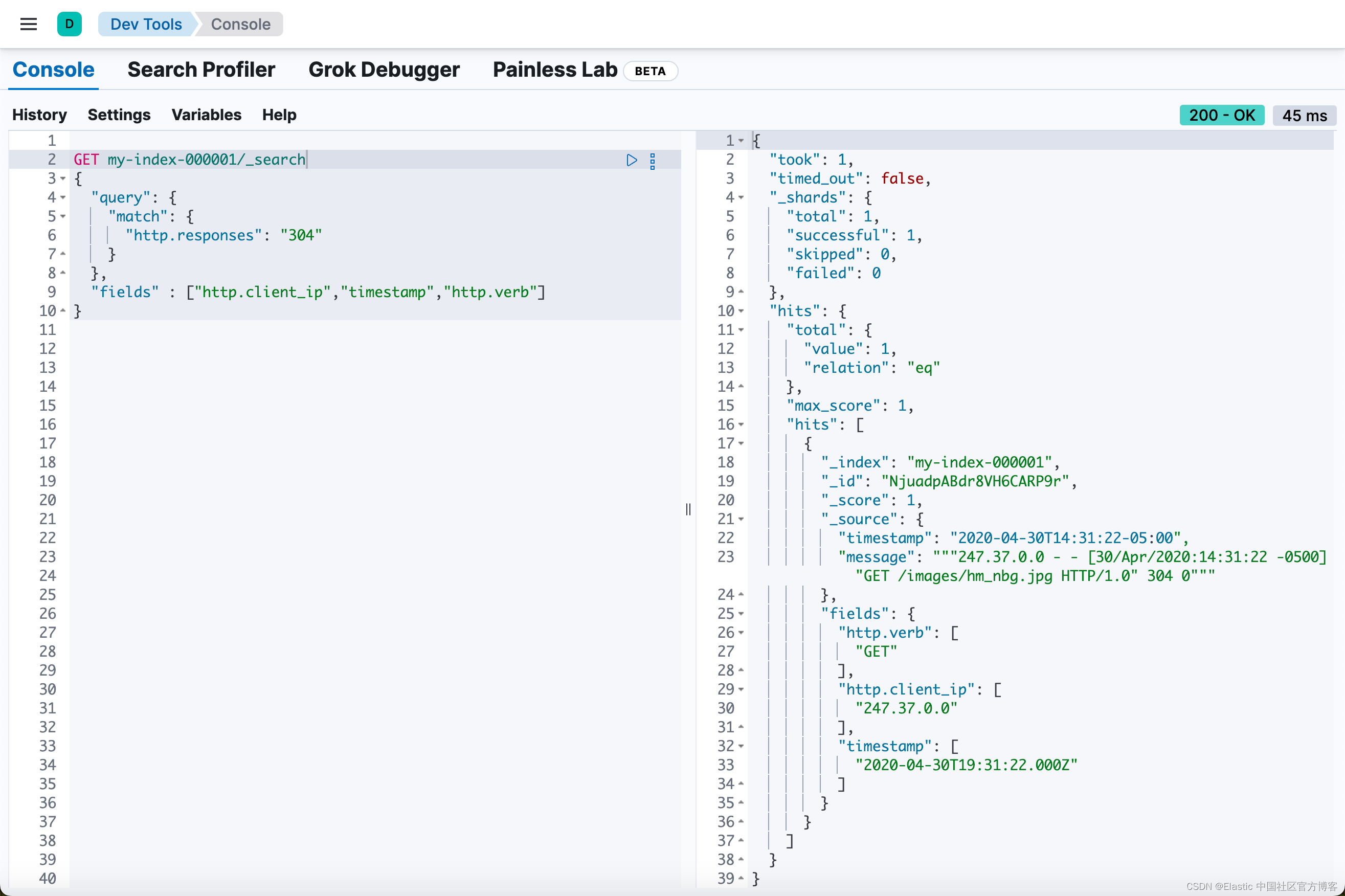
Elasticsearch:Runtime fields - 运行时字段(二)
这是继上一篇文章 “Elasticsearch:Runtime fields - 运行时字段(一)” 的续篇。 在查询时覆盖字段值 如果你创建的运行时字段与映射中已存在的字段同名,则运行时字段会隐藏映射字段。在查询时,Elasticsearch 会评估运…...
)
Python正则表达式的入门用法(上)
Python正则表达式是使用re模块来进行操作的。re模块提供了一组函数,用于进行字符串的匹配和查找操作。 下面是Python中使用正则表达式的一些常用函数: re.search(pattern, string):在字符串中查找并返回第一个匹配的对象。 re.match(patte…...
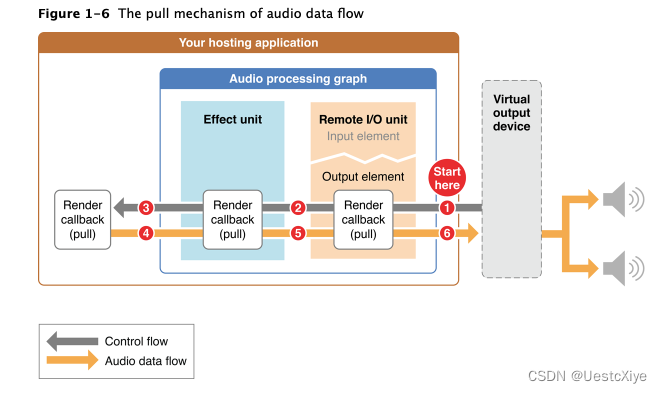
Audio Processing Graphs 管理 Audio Units
Audio Processing Graphs 管理 Audio Units Audio Processing Graphs 管理 Audio UnitsAudio Processing Graph 拥有精确的 I/O UnitAudio Processing Graph 提供线程安全通过 graph "pull" 音频流 Audio Processing Graphs 管理 Audio Units audio processing grap…...

欧盟,又出了新规-通用充电器新规通用充電器的 RED 修正案如何办理?
欧盟,又出了新规-通用充电器新规通用充電器的 RED 修正案如何办理? 欧盟新规委员会发布《通用充电器指令》指南通用充電器的 RED 修正案办理流程: 2024年5月7日,欧盟委员会发布《通用充电器指令》指南,修订了《无线…...
thinkphp6/8 验证码
html和后台验证代码按官方来操作 ThinkPHP官方手册 注意: 如果验证一直失败,看看Session是否开启, 打印dump(session_status());结果2为正确的, PHP_SESSION_DISABLED: Session功能被禁用(返回值为0)。…...
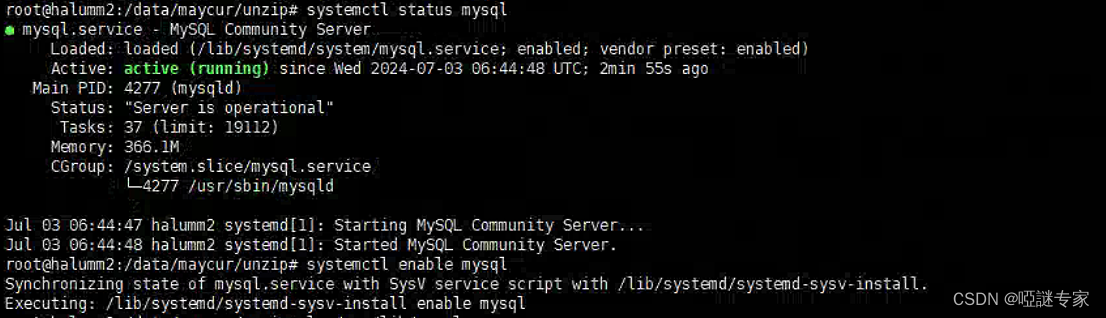
Ubuntu 22.04 LTS 上安装 MySQL8.0.23(在线安装)
目录 在线安装MySQL 步骤1:更新软件包列表 步骤2:安装MySQL服务器 步骤3:启动MySQL服务 步骤4:检查MySQL状态 步骤5:修改密码、权限 在线安装MySQL 步骤1:更新软件包列表 在进行任何软件安装之前&a…...
如何选择优质模型?SD3性能究竟如何?
遇到难题不要怕!厚德提问大佬答! 厚德提问大佬答12 厚德提问大佬答第十二期 你是否对AI绘画感兴趣却无从下手?是否有很多疑问却苦于没有大佬解答带你飞?从此刻开始这些问题都将迎刃而解!你感兴趣的话题,厚德…...
)
Linux上脚本备份数据库(升级版)
直接上代码: #!/bin/bash# 配置部分 mysql_user"root" mysql_host"localhost" mysql_port"3306" mysql_charset"utf8mb4" mysql_defaults_file"/home/mysql/mysql_back/.my.cnf"backup_base_dir"/mnt/sdd/…...

【深度解析】滑动窗口:目标检测算法的基石
标题:【深度解析】滑动窗口:目标检测算法的基石 目标检测是计算机视觉领域的一个核心任务,旨在识别图像中所有感兴趣的目标,并确定它们的位置和大小。滑动窗口方法作为目标检测中的一种传统技术,虽然在深度学习时代逐…...

约束:对于数据的限制
主键约束 主键约束:唯一约束非空约束,该字段上的数据不能重复且不能为null 注意:一张表必须有且只有一个主键 添加主键约束 -- 方式一(推荐) CREATE TABLE user(username VARCHAR(32) PRIMARY KEY,password VARCHAR(32),nick_name VARCHAR(3…...

【总线】AXI4第七课时:AXI的额外的控制信息(PROT和CACHE)
大家好,欢迎来到今天的总线学习时间!如果你对电子设计、特别是FPGA和SoC设计感兴趣,那你绝对不能错过我们今天的主角——AXI4总线。作为ARM公司AMBA总线家族中的佼佼者,AXI4以其高性能和高度可扩展性,成为了现代电子系统中不可或缺的通信桥梁…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...


