k8s_如何配置 containerd 使用镜像加速拉取docker.io上的镜像
在 Kubernetes 使用 containerd 作为容器运行时,可以通过配置 containerd 来使用镜像网站(镜像仓库)拉取镜像。这可以通过修改 containerd 的配置文件来实现。以下是详细步骤:
步骤 1:安装 containerd (如果已安装,这一步略过)
如果尚未安装 containerd,可以使用以下命令安装(以 CentOS 为例):
sudo yum update -y
sudo yum install -y containerd
步骤 2:配置 containerd
-
创建 containerd 配置文件(如果还没有):
sudo mkdir -p /etc/containerd containerd config default | sudo tee /etc/containerd/config.toml -
编辑配置文件:
打开
/etc/containerd/config.toml文件:sudo nano /etc/containerd/config.toml -
配置镜像加速:
找到
[plugins."io.containerd.grpc.v1.cri".registry.mirrors]部分,并添加你的镜像网站地址。例如,使用docker.io镜像仓库:[plug
相关文章:

k8s_如何配置 containerd 使用镜像加速拉取docker.io上的镜像
在 Kubernetes 使用 containerd 作为容器运行时,可以通过配置 containerd 来使用镜像网站(镜像仓库)拉取镜像。这可以通过修改 containerd 的配置文件来实现。以下是详细步骤: 步骤 1:安装 containerd (如果已安装,这一步略过) 如果尚未安装 containerd,可以使用以下命…...

centos7安装宝塔面板
一、进入root模式 sudo su二、安装宝塔面板 if [ -f /usr/bin/curl ];then curl -sSO https://download.bt.cn/install/install_panel.sh;else wget -O install_panel.sh https://download.bt.cn/install/install_panel.sh;fi;bash install_panel.sh ed8484bec...

Spring 事务管理:全面解析
Spring 框架是一款广受欢迎的 Java 开发框架,其强大的功能之一便是事务管理。事务管理在确保数据一致性和完整性方面至关重要。在这篇文章中,我们将深入探讨 Spring 事务管理,包括声明式事务管理、编程式事务管理,以及事务传播和隔…...

概率论与数理统计_上_科学出版社
contents 前言第1章 事件与概率1.1 随机事件与样本空间1.1.1 样本空间1.1.2 随机事件1.1.3 事件之间的关系与运算 1.2 概率的三种定义及其性质1.2.1 概率的统计定义1.2.2 概率的古典定义1.2.3 概率的几何定义1.2.4 概率的性质 1.3 常用概型公式1.3.1 条件概率计算公式1.3.2 乘法…...

昇思25天学习打卡营第11天|LSTM+CRF序列标注
序列标注指给定输入序列,给序列中每个Token进行标注标签的过程。序列标注问题通常用于从文本中进行信息抽取,包括分词(Word Segmentation)、词性标注(Position Tagging)、命名实体识别(Named Entity Recognition, NER)等。 和人理解语言一样,…...
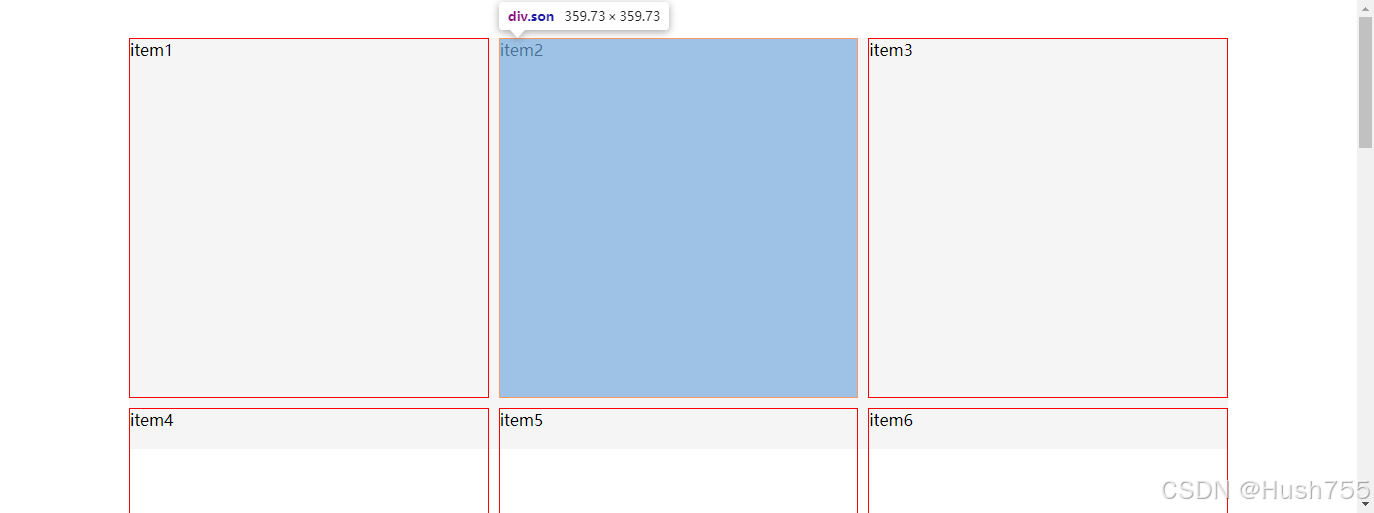
CSS 核心知识点 - grid
思维导图 参考网址: https://developer.mozilla.org/zh-CN/docs/Web/CSS/CSS_grid_layout 一、什么是 grid? CSS Grid布局是在CSS3规范中引入的一种新的布局方式,旨在解决传统布局方法(如浮动、定位、表格布局)存在的许多问题。C…...
)
pyecharts可视化案例大全(1~10)
pyecharts可视化案例大全 一、堆叠柱状图二、关闭坐标轴显示三、自定义坐标轴标签文本四、更改坐标轴数据类型五、双Y轴【直方图&折线图】六、直方图——双Y轴七、折线图——双X轴八、图例选择设置单选九、缩略轴——inside组件十、缩略轴——slider组件一、堆叠柱状图 不…...

SpringBoot 启动流程一
SpringBoot启动流程一 我们首先创建一个新的springboot工程 我们不添加任何依赖 查看一下pom文件 我们创建一个文本文档 记录我们的工作流程 我们需要的是通过打断点实现 我们首先看一下启动响应类 package com.bigdata1421.start_up;import org.springframework.boot.Spr…...
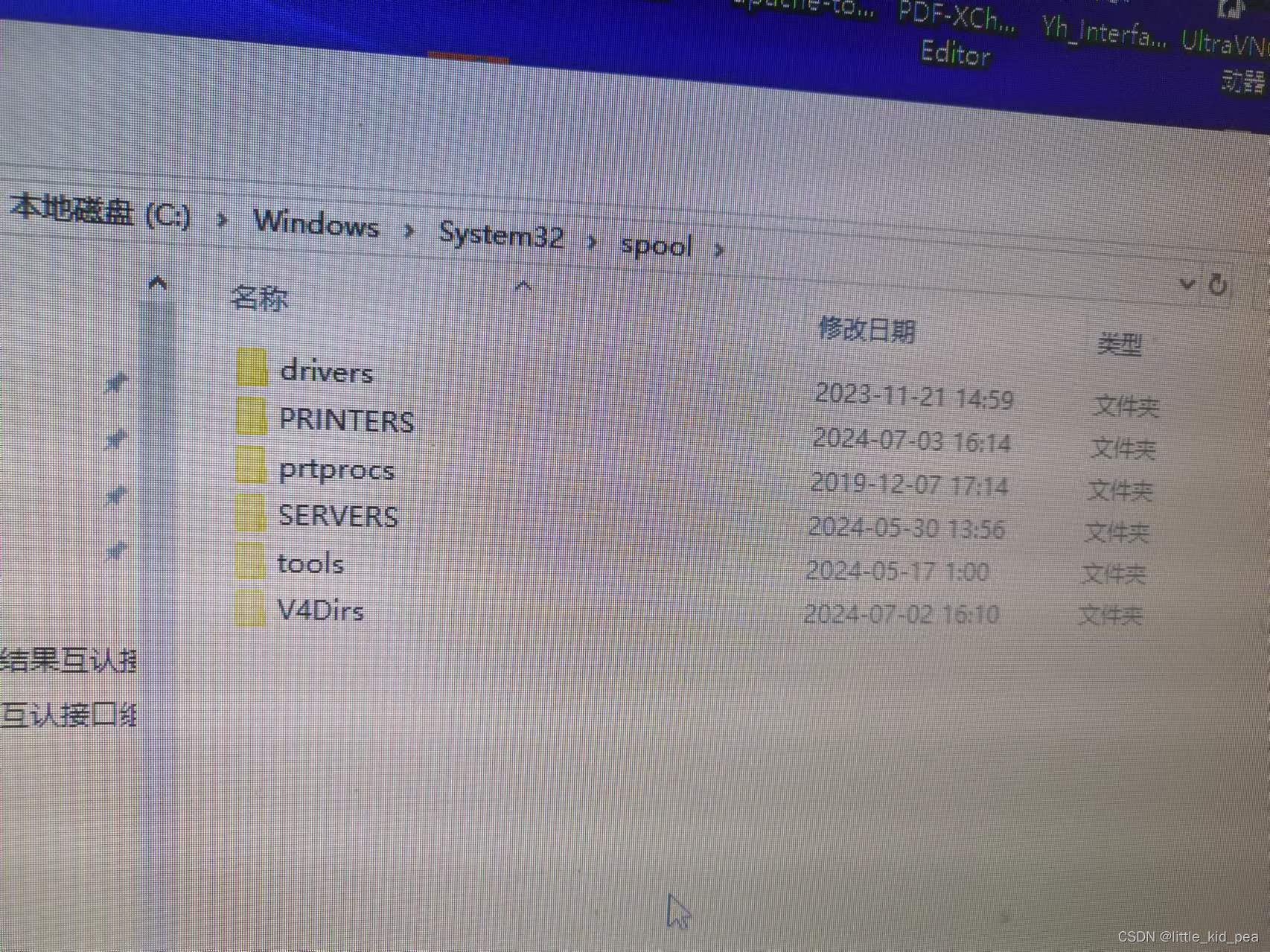
打印机删除副本以后无法安装打印机驱动
根据知乎文章解决打印机驱动副本存在多个,打印机驱动无法删除,或者驱动包无法删除等问题。的方法删除打印机副本以后发现无论如何也装不上驱动了。 要么驱动安装成功,但是设备仍然是指定状态。 后面发现是删错文件夹了,教程里让删…...

Vue3中为Ant Design Vue中Modal.confirm自定义内容
在一次业务开发时代码时,碰到了一种既想要Modal.confirm样式,又想要定制其content内容的情况。 大部分情况下,使用Modal.method()这种方式时,可能content内容固定都是字符串,那如果想要做更高级的交互怎么办ÿ…...

智能猫砂盆到底哪家好用?自费实测聚宠、糯雪、CEWEY真实反馈!
快到夏天了,是不是还有人因为没挑选到喜欢的智能猫砂盆而苦恼着?太便宜怕不好用,太贵怕质量比不上价格。来来去去拖到现在还没决定,我作为养了四年猫的资深铲屎官,今天就来给大家传授经验,关于我是怎么从好…...

初阶数据结构之二叉树
那么本篇文是初阶数据结构这个系列的最后一篇文章,那么闲话少叙,我们直接进入正题 在讲二叉树的一些之前知识点之前,我先给大家送个小礼物哈 手搓二叉树 typedef int BTDataType ; typedef struct BinaryTreeNode { BTDataType _data …...

代码随想三刷动态规划篇8
代码随想三刷动态规划篇8 122. 买卖股票的最佳时机 II题目代码 123. 买卖股票的最佳时机 III题目代码 188. 买卖股票的最佳时机 IV题目代码 309. 买卖股票的最佳时机含冷冻期题目代码 122. 买卖股票的最佳时机 II 题目 链接 代码 class Solution {public int maxProfit(int…...

服务拆分的原则
目录 一、单一职责原则 二、服务自治原则 三、单向依赖 一、单一职责原则 单⼀职责原则原本是面向对象设计中的⼀个基本原则, 它指的是⼀个类应该专注于单⼀功能. 不要存在多于⼀个导致类变更的原因 在微服务架构中, ⼀个微服务也应该只负责⼀个功能或业务领域, 每个服务应该…...
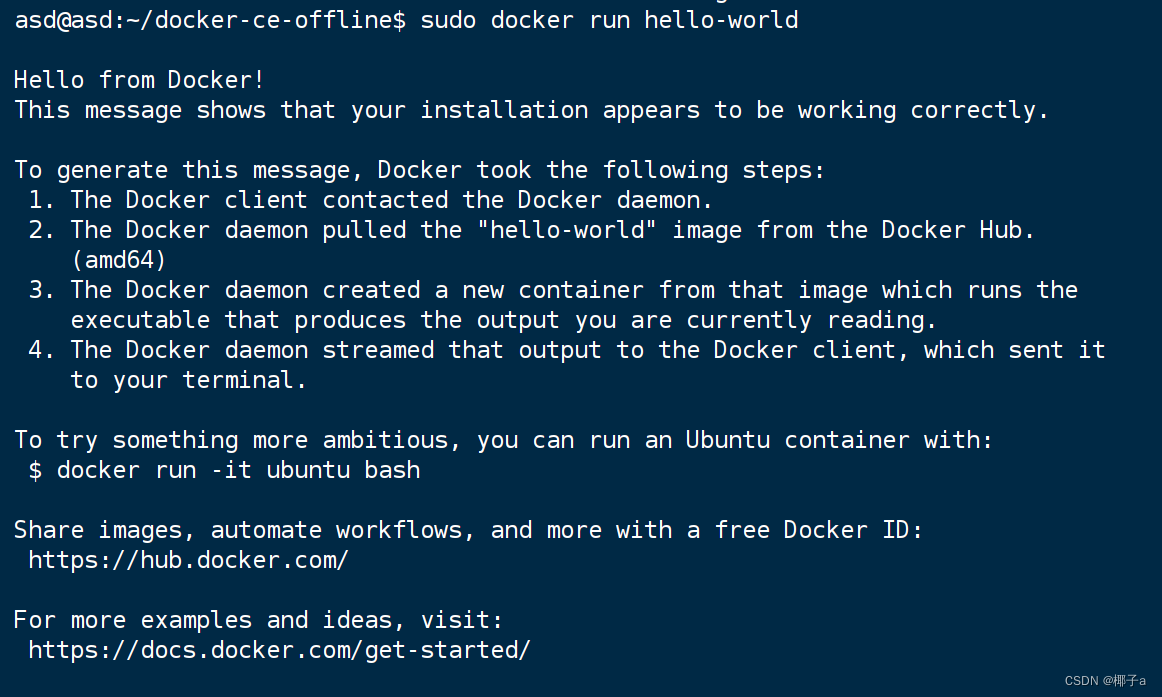
离线安装docker社区版
提示:以下所有命令都在Ubuntu-24.04-live-server-amd64系统中运行 文章目录 前言一、离线包制作二、在目标系统上离线安装Docker CE总结 前言 安全原因,内部机器不能联网,要给新机器安装 docker-ce 只能使用离线安装方法。如果使用本文的下载…...

徒手绘制 Android 通用进度条
拖动条(FlexSeekBar),在Android的各个地方都非常常用,本文旨在自研一套通用的进度条,非常适合车载App使用 样式如下: 使用示例 <!--默认用法--> <com.max.android.ui.seekbar.FlexSeekBarandroi…...
【TB作品】矩阵键盘电话拨号,ATMEGA16单片机,Proteus仿真 atmega16矩阵键盘电话拨号
atmega16矩阵键盘电话拨号 c代码和仿真图: 使用ATmega16实现矩阵键盘电话拨号功能 项目背景 在电子设计和嵌入式系统开发中,矩阵键盘是常见的人机交互方式。它可以实现较多按键的输入,同时节省单片机的I/O资源。结合LCD显示和蜂鸣器&am…...

JavaScript(6)——数据类型转换
为什么需要类型转换? JavaScript是弱数据类型:JavaScript不知道变量到底属于哪种数据类型,只有赋值了才清除 使用表单,prompt获取的数据默认为字符串类型,此时不能直接进行算数运算 隐式转换 某些运算符被执行时&am…...

概率论与数理统计_下_科学出版社
contents 前言第5章 大数定律与中心极限定理独立同分布中心极限定理 第6章 数理统计的基本概念6.1 总体与样本6.2 经验分布与频率直方图6.3 统计量6.4 正态总体抽样分布定理6.4.1 卡方分布、t 分布、F 分布6.4.2 正态总体抽样分布基本定理 第7章 参数估计7.1 点估计7.1.1 矩估计…...

Android 复习layer-list使用
<shape android:shape"rectangle"> <size android:width"1dp" android:height"100px" /> <solid android:color"#FFFFFF" /> </shape> 通过shape画线段,通过 <item android:gravity"left|top"…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
