Games101学习笔记 Lecture16 Ray Tracing 4 (Monte Carlo Path Tracing)
Lecture16 Ray Tracing 4 (Monte Carlo Path Tracing
- 一、蒙特卡洛积分 Monte Carlo Integration
- 二、路径追踪 Path tracing
- 1.Whitted-Style Ray Tracing's Problems
- 2.只考虑直接光照时
- 3.考虑全局光照
- ①考虑物体的反射光
- ②俄罗斯轮盘赌 RR (得到正确shade函数)
- ③射线生成(追踪足够多的path)
- ④对光源进行采样
- 推导
- ⑤结束
一、蒙特卡洛积分 Monte Carlo Integration
- 为什么:用于解决难以求解的积分问题
- 是什么/怎么办:在x轴上随机采样积分,而不是均匀采样

- 函数 f(x) 在区间 [a,b] 上的定积分 ∫ a b f ( x ) d x \int_{a}^{b}f(x)dx ∫abf(x)dx
- 随机变量 X i ∼ p ( x ) X_{i} \sim p(x) Xi∼p(x)
- 得到蒙特卡洛积分为 F N = 1 N ∑ i = 1 N f ( X i ) p ( X i ) F_{N} = \frac{1}{N} \sum_{i=1}^{N} \frac{f(X_{i})}{p(X_{i})} FN=N1∑i=1Np(Xi)f(Xi)
二、路径追踪 Path tracing
1.Whitted-Style Ray Tracing’s Problems
- 只处理镜面或者透明物体的反射和折射,在漫反射时就停止了,忽略了物体之间的反射
- 在glossy金属材质时,不应该全部都反射
- 但是 渲染方程是对的
- L r ( p , ω r ) L_{r}(p, ω_{r}) Lr(p,ωr) = L e ( p , ω o ) L_{e}( p, ω_{o}) Le(p,ωo) + ∫ Ω + L r ( p , − ω i ) f r ( p , ω i , ω r ) ( n ⋅ ω i ) d w i \int_{Ω^+}^{} L_{r}( p , -ω_{i}) f_{r}( p , ω_{i} ,ω_{r}) ( n \cdot ω_{i})dw_{i} ∫Ω+Lr(p,−ωi)fr(p,ωi,ωr)(n⋅ωi)dwi
2.只考虑直接光照时
- L o ( p , ω o ) L_{o}(p, ω_{o}) Lo(p,ωo) = ∫ Ω + L i ( p , ω i ) f r ( p , ω i , ω o ) ( n ⋅ ω i ) d w i \int_{Ω^+}^{} L_{i}( p , ω_{i}) f_{r}( p , ω_{i} ,ω_{o}) (n\cdotω_{i})dw_{i} ∫Ω+Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)dwi 用蒙特卡罗积分求解 F N = 1 N ∑ i = 1 N f ( X i ) p ( X i ) F_{N} = \frac{1}{N} \sum_{i=1}^{N} \frac{f(X_{i})}{p(X_{i})} FN=N1∑i=1Np(Xi)f(Xi)
- f(x) 是 L i ( p , ω i ) f r ( p , ω i , ω o ) ( n ⋅ ω i ) L_{i}(p,ω_{i})f_{r}(p,ω_{i},ω_{o})(n\cdotω_{i}) Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)
- pdf(概率密度函数)是 “对半球进行采样” p ( ω i ) = 1 2 Π p(ω_{i}) = \frac{1}{2Π} p(ωi)=2Π1
- 得到式子 L o ( p , ω o ) L_{o}(p, ω_{o}) Lo(p,ωo) = 1 N ∑ i = 1 N L i ( p , ω i ) f r ( p , ω i , ω o ) ( n ⋅ ω i ) p ( ω i ) \frac{1}{N} \sum_{i=1}^{N} \frac{L_{i}(p,ω_{i})f_{r}(p,ω_{i},ω_{o})(n\cdotω_{i})}{p(ω_{i})} N1∑i=1Np(ωi)Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi) 是正确的直接光照公式

3.考虑全局光照
①考虑物体的反射光

- Q同样也反射光线到P上(方向上也相当于P到Q点的光)

- Q 的直接光照 = Q 到 P 的反射
- 但是这样做光线会有 指数级增长

- 假设只有一根光线时(只选择一个方向 ω i ω_{i} ωi )

- 但递归需要停止,不然计算量无限增加(但又想保证质量)—— 俄罗斯轮盘赌 RR
②俄罗斯轮盘赌 RR (得到正确shade函数)
- 通过随机概率选择是否继续追踪光线,可以有效地控制光线数量,并避免能量损失过多
- 实现步骤
- 设置一个概率 P
- 以概率 P 发射光线:若随机数< P,则发射并计算光线亮度 Lo
- 以概率 1-P 不发射光线:若随机数 ≥ P,不发射光线,认为亮度为0
- 能量补偿:由于第三步会导致能量损失,为了弥补损失,需要将得到的光线亮度 Lo 除以 P,即 Lo/P,可以保证期望值不变

③射线生成(追踪足够多的path)
- 1.在 每个像素内均匀选择多个采样点
- 2.并为每个采样点发射一条光线,
- 3.然后使用路径追踪算法 计算每条光线的亮度
- 4.将他们 平均起来得到像素最终亮度

④对光源进行采样

- 由于光源相对于半球来说比较小,所以 每个采样点发射的光线中,只有很少一部分会击中光源(有很少的光会从光源击中半球上被采样到的点),用均匀采样会导致浪费
- 光源对场景的贡献亮度远远大于了其他方向,应该 更多地采样光源方向,提高效率
推导
- 假设光源面积为 A —— pdf = 1 A \frac{1}{A} A1
- 渲染方程在立体角上的积分 Lo = ∫ L i ⋅ f r ⋅ c o s d ω \int Li\cdot fr\cdot cos dω ∫Li⋅fr⋅cosdω —— 这个积分代表场景中一点的亮度Lo 是半球上 所有方向的光线亮度和反射率的积分
- 为了使用蒙特卡洛积分来估计场景中一点的亮度Lo,我们需要将渲染方程转化为对光源的积分
- 数学的转化,需要找到 立体角 dω 和光源表面积 dA 之间的关系 —— 光源面积立体角方向在球面上的投影
- 立体角的求法:球面面积法 ω = S / r 2 ω = S/r^2 ω=S/r2 —— d ω = d A c o s θ ′ ∣ x ′ − x ∣ 2 dω = \frac{dA cosθ'}{|x'-x|^2} dω=∣x′−x∣2dAcosθ′

- 此时重写渲染方程 Lo = ∫ A L i ( x , ω i ) f r ( x , ω i , ω o ) c o s θ c o s θ ′ ∣ x ′ − x ∣ 2 d A \int_{A}^{} L_{i}( x, ω_{i}) f_{r}( x, ω_{i} ,ω_{o})\frac{cosθcosθ'}{|x'-x|^2}dA ∫ALi(x,ωi)fr(x,ωi,ωo)∣x′−x∣2cosθcosθ′dA
- 可以写出蒙特卡洛积分 f(x) = L i ( x , ω i ) f r ( x , ω i , ω o ) c o s θ c o s θ ′ ∣ x ′ − x ∣ 2 L_{i}( x, ω_{i}) f_{r}( x, ω_{i} ,ω_{o})\frac{cosθcosθ'}{|x'-x|^2} Li(x,ωi)fr(x,ωi,ωo)∣x′−x∣2cosθcosθ′,pdf = 1/A
⑤结束
- 来自于光源的进行光源采样,计算直接光照;其他非光源的就需要RR,计算间接光照

- 还得判断光源有没有被遮挡

相关文章:

Games101学习笔记 Lecture16 Ray Tracing 4 (Monte Carlo Path Tracing)
Lecture16 Ray Tracing 4 (Monte Carlo Path Tracing 一、蒙特卡洛积分 Monte Carlo Integration二、路径追踪 Path tracing1.Whitted-Style Ray Tracings Problems2.只考虑直接光照时3.考虑全局光照①考虑物体的反射光②俄罗斯轮盘赌 RR (得到正确shade函数&#x…...
数据结构概念
文章目录 1. 概念 2. 数据结构和算法的关系 3. 内存 4. 数据的逻辑结构 5. 数据的存储结构 1. 顺序存储结构 2. 链式存储结构 3. 索引存储结构 4. 散列存储结构 6. 数据的运算 1. 概念 定义1(宏观): 数据结构是为了高效访问数据而…...
Windows 下载安装ffmpeg
下载地址 https://ffmpeg.org/download.html 测试 管理员方式打开控制台,输入ffmpeg测试 配置环境变量...

Java AI 编程助手
Java AI 编程助手是指利用人工智能技术来增强和优化Java开发过程中的各种任务和活动。它可以涵盖从代码生成和分析到测试和优化的多个方面,帮助开发人员提高生产效率、降低错误率,并优化代码质量和性能。 ### 功能和特点 1. **智能代码生成和建议**&am…...

day10:01集合
1 作用 Python中的集合(Set)是一个无序的、不包含重复元素的容器。它主要用于去重、成员测试、以及执行数学上的集合运算(如并集、交集、差集和对称差集)等操作。集合的内部实现通常基于哈希表,这提供了快速的成员测试…...

03浅谈提示工程、RAG和微调
03浅谈提示工程、RAG和微调 提示词Prompt Prompt(提示词)是指在使用大模型时,向模型提供的一些指令或问题。这些指令作为模型的输入,引导模型产生所需要的输出。例如,在生成文本时,Prompt可能是一个问题或…...

硅纪元视角 | AI纳米机器人突破癌症治疗,精准打击肿瘤细胞
在数字化浪潮的推动下,人工智能(AI)正成为塑造未来的关键力量。硅纪元视角栏目紧跟AI科技的最新发展,捕捉行业动态;提供深入的新闻解读,助您洞悉技术背后的逻辑;汇聚行业专家的见解,…...

刷代码随想录有感(125):动态规划——最长公共子序列
题干: 代码: class Solution { public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>>dp(text1.size() 1, vector<int>(text2.size() 1, 0));for(int i 1; i < text1.size(); i){for(int j …...

Linux和mysql中的基础知识
cpu读取的指令大部分在内存中(不考虑缓存) 任何程序在运行之前都的加入到内存。 eip->pc指针,指明当前指令在什么位置。 代码大概率是从上往下执行的,基于这样的基本理论。既可以将一部分指令加载到CPU对应的缓存中…...
编辑 12 编辑模版)
ArcGIS Pro SDK (七)编辑 12 编辑模版
ArcGIS Pro SDK (七)编辑 12 编辑模版 文章目录 ArcGIS Pro SDK (七)编辑 12 编辑模版1 在图层上按名称查找编辑模板2 查找属于独立表的表模板3 当前模板4 更改模板的默认编辑工具5 隐藏或显示模板上的编辑工具6 使用图层创建新模…...
)
数据结构底层之HashMap(面经篇1)
1 . 讲一下hashmap的数据结构 HashMap是一种基于哈希表实现的数据结构,通常用于关联键值对,其中键是唯一的,而值可以重复。在Java中,HashMap是java.util.Map接口的一个实现,它提供了快速的查找、插入和删除操作。 数据…...

昇思学习打卡-6-基于MindSpore的GPT2文本摘要
第一次近距离接触GPT,了解了tokenizers这个分词库,感觉NLP和CV对比起来,处理流程基本一致,都是数据集加载和处理,模型构建、选择学习率、模型训练,进而可以使用模型进行推理。 不同的是,NLP可能…...
代码随想录算法训练营第2天|LeetCode977,209,59
977.有序数组平方 题目链接: 977. 有序数组的平方 - 力扣(LeetCode) 文章讲解:代码随想录 视频讲解: 双指针法经典题目 | LeetCode:977.有序数组的平方_哔哩哔哩_bilibili 第一想法 暴力算法肯定是先将元素…...

Web前端开发——HTML快速入门
HTML:控制网页的结构CSS:控制网页的表现 一、什么是HTML、CSS (1)HTML (HyperText Markup Languaqe:超文本标记语言) 超文本:超越了文本的限制,比普通文本更强大。除了…...

浅谈http协议及常见的面试题
1、浅谈http协议 HTTP(Hypertext Transfer Protocol)超文本传输协议,是互联网上应用最为广泛的一种网络协议,所有的WWW文件都必须遵守这个标准。它是基于TCP/IP通信协议来传递数据(HTML文件、图片文件、查询结果等&am…...
LabVIEW自动探头外观检测
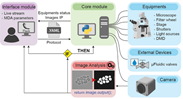
开发了一套基于LabVIEW的软件系统,结合视觉检测技术,实现探头及连接器外观的自动检测。通过使用高分辨率工业相机、光源和机械手臂,系统能够自动定位并检测探头表面的细微缺陷,如划痕、残胶、异色、杂物等。系统支持多种探头形态&…...

搏击与防卫笔记
文章目录 降龙十八掌 咏春个人防身笔记防卫直拳应对耳光防卫摆拳坐马冲拳 本来想以武术为标题的,想了想武术这个标题太大太深,自己连一知半解都算不上,就谢为搏击与防卫吧。 每个男孩都有个武侠梦,独步江湖,仗剑走天涯…...
泰国内部安全行动司令部数据泄露
BreachForums 论坛的一名成员宣布发生一起重大数据泄露事件,涉及泰国内部安全行动司令部 (ISOC),该机构被称为泰国皇家武装部队的政治部门。 目前,我们无法准确确认此次泄露的真实性,因为该组织尚未在其网站上发布有关该事件的任…...
)
MATLAB算法实战应用案例精讲-【数模应用】分层聚类(附MATLAB、python和R语言代码实现)
目录 前言 几个高频面试题目 什么情况下选择分层聚类,什么情况下选择K-mean聚类呢?两种模型的好坏如何比较? 算法原理 SPSSAU 案例分析 SPSSPRO 1、作用 2、输入输出描述 3、案例示例 4、案例数据 5、案例操作 6、输出结果分析 7、注意事项 8、模型理论 分层…...

九、函数的声明和定义
函数声明: 1. 告诉编译器有一个函数叫什么,参数是什么,返回类型是什么。但是具体是不是存在,函数 声明决定不了。 2. 函数的声明一般出现在函数的使用之前。要满足先声明后使用。 3. 函数的声明一般要放在头文件中的。 定义的函…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
