LeetCode刷题之HOT100之完全平方数
2024 7/7 转眼间就到周日啦!昨天下午开组会,开了三个半小时。如坐针毡,会后跑了个步、洗了个澡、洗了衣服、躺床上看了会《罪与罚》,睡着了。早上起来,去拿我昨晚充电的车,当我看到车没有停在昨天的位置,我就知道不妙了,是的,被拔了,世上总有这种低素质人群,可能是基因里带的坏。天气除了热,景色还是不错的,附两张图

图1、南校区视角

图2、图片左边是一只蝴蝶,本来是两只的
okok,做题啦
1、题目描述

2、算法分析
给一个整数n,要求返回和为n的完全平方数的最少数量。
测试用例有两个,分别为12、13。根据测试案例以及面向对象思想,我编写出了以下代码:
public int numSquares(int n) {if(n == 12){return 3;}if(n == 13){return 2;}return 0;}
很显然,通过案例,但是提交出错了,那么我们得想出一种合适的算法来求解。题目可以分解为:
求完全平方数;
下一步就是如何求和为n的完全平方数的最少数量了;
这一步怎么写出来呢?
我的方案就是:
看题解。
题解给出的也是dp思想,大致思路:
算法思路如下:
- 定义状态:我们定义一个数组
dp,其中dp[i]表示将整数i表示为完全平方数之和的最少个数。 - 初始化状态:对于
dp[0],由于0不需要任何平方数来表示,所以dp[0] = 0。 - 状态转移方程:对于每个
i(从1到n),我们遍历所有可能的平方数j*j(其中j*j <= i)。对于每个这样的平方数,我们检查dp[i - j*j]的值,即表示i - j*j为平方数之和的最少个数。然后,我们更新dp[i]为所有可能的
dp[i - j * j] + 1中的最小值(其中+1是因为我们加上了当前的平方数j*j)。这样,我们就得到了将i表示为平方数之和的最少个数。 - 计算结果:最终,
dp[n]将包含将n表示为平方数之和的最少个数,这就是我们要找的答案。
3、代码
public int numSquares(int n) {// 创建一个长度为 n+1 的数组 dp,用于存储从 0 到 n 每个数表示为平方数之和的最少个数int[] dp = new int [n + 1];// 遍历从1到n的每个数 for(int i = 1; i <= n; i++){// 初始化minN为最大值,用于寻找最小的平方数组合数量 int minN = Integer.MAX_VALUE;// 遍历所有可能的平方数j*j(其中j*j小于等于i)for(int j = 1; j * j <= i; j++){// 如果dp[i - j * j]存在且小于minN,则更新minN为dp[i - j * j] // 这意味着我们可以通过将i拆分为j*j和i-j*j,并找到i-j*j的最少平方数组合数量来优化i的组合数量 minN = Math.min(minN, dp[i - j * j]);}// 更新dp[i]为将i表示为平方数之和的最少个数,即minN+1(因为我们要加上当前的平方数j*j)dp[i] = minN + 1;}// 返回dp[n],即将n表示为平方数之和的最少个数return dp[n];}
4、复杂度分析
- 时间复杂度: O ( n n ) O(n\sqrt{n}) O(nn)。其中 n 为给定的正整数。状态转移方程的时间复杂度为 O ( n ) O(\sqrt{n}) O(n)。共需要计算 n
个状态,因此总时间复杂度为 O ( n n ) O(n\sqrt{n}) O(nn)。 - 空间复杂度: O ( n ) O(n) O(n)。我们需要 O(n) 的空间保存状态。
okok,写完啦,在IDE上打断点debug后也是对其加深理解了,再见,坐等外卖啦!
相关文章:

LeetCode刷题之HOT100之完全平方数
2024 7/7 转眼间就到周日啦!昨天下午开组会,开了三个半小时。如坐针毡,会后跑了个步、洗了个澡、洗了衣服、躺床上看了会《罪与罚》,睡着了。早上起来,去拿我昨晚充电的车,当我看到车没有停在昨天的位置&am…...

【SpringCloud应用框架】Nacos集群架构说明
第六章 Spring Cloud Alibaba Nacos之集群架构说明 文章目录 前言一、Nacos支持三种部署模式二、集群部署说明三、预备环境 前言 到目前为止,已经完成了对Nacos的一些基本使用和配置,接下来还需要了解一个非常重要的点,就是Nacos的集群相关的…...

JS进阶-作用域
学习目标: 掌握作用域 学习内容: 作用域局部作用域全局作用域作用域链JS垃圾回收机制拓展-JS垃圾回收机制-算法说明闭包变量提升 作用域: 作用域规定了变量能够被访问的"范围",离开了这个"范围"变量便不能被…...
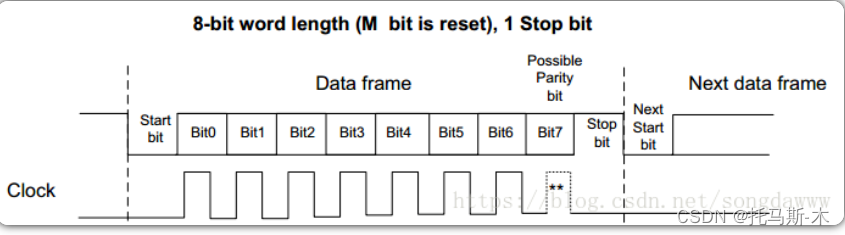
stm32 使用GPIO模拟串口发送
在STM32微控制器上实现模拟串口输出(也称为软件串口或比特邦定(Bit-Banging)串口),主要是因为硬件上的UART资源有限或者为了特定需求而需要更多的串口通信接口。模拟串口意味着使用GPIO引脚模拟UART的TX(发…...

数据的统计探针:SKlearn中的统计分析方法
数据的统计探针:SKlearn中的统计分析方法 在数据科学领域,统计分析是理解和解释数据的关键工具。Scikit-learn(简称sklearn),作为Python中一个功能强大的机器学习库,提供了多种方法来进行数据的统计分析。…...

实例演示Kafka-Stream消息流式处理流程及原理
以下结合案例:统计消息中单词出现次数,来测试并说明kafka消息流式处理的执行流程 Maven依赖 <dependencies><dependency><groupId>org.apache.kafka</groupId><artifactId>kafka-streams</artifactId><exclusio…...
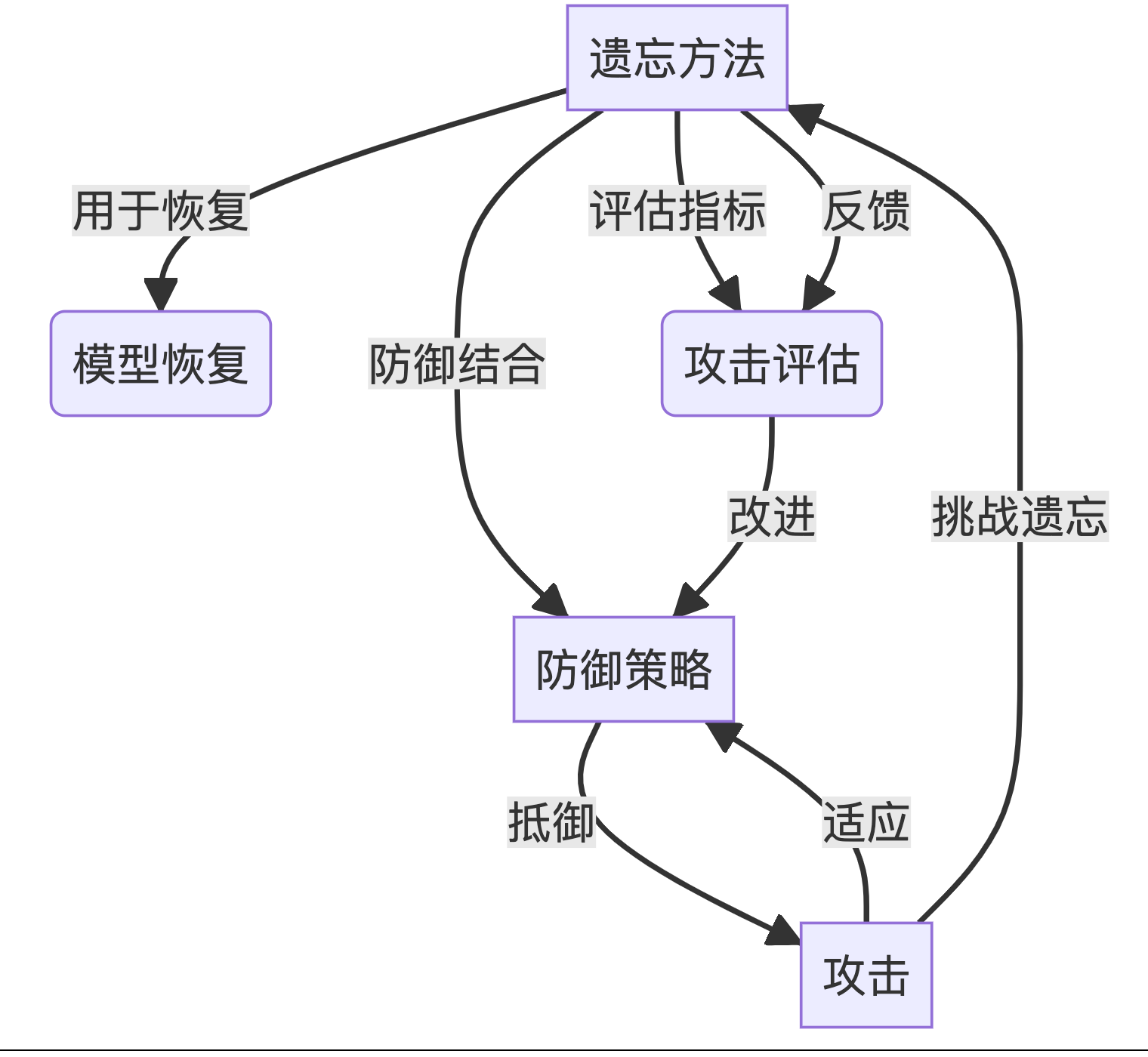
【博士每天一篇文献-综述】Threats, Attacks, and Defenses in Machine Unlearning A Survey
1 介绍 年份:2024 作者:刘子耀,陈晨,南洋理工大学 期刊: 未发表 引用量:6 Liu Z, Ye H, Chen C, et al. Threats, attacks, and defenses in machine unlearning: A survey[J]. arXiv preprint arXiv:2403…...

Python数据分析实战,运输车辆驾驶行为分析,案例教程编程实例课程详解
引言 运输车辆的安全驾驶行为分析是确保道路安全、提高运输效率的重要环节。随着数据采集技术的发展和数据分析工具的普及,利用Python进行数据分析已成为这一领域的重要工具。本文将详细介绍如何使用Python进行运输车辆驾驶行为分析,涵盖数据采集、数据预处理、数据分析及结果…...

网络安全法对等级保护中的权利和义务有何规范?
在数字时代的交响乐章中,网络安全法与等级保护共同编织了一曲关于权利与义务的和谐旋律。《中华人民共和国网络安全法》作为我国网络安全领域的基本法,对等级保护提出了明确的规范,旨在构建一个安全、有序的网络空间。本文将深入解析网络安全…...

苹果清理软件:让你的设备焕然一新
随着时间的推移,无论是Mac电脑还是iOS设备,都可能会因为积累的垃圾文件、缓存、未使用的应用和其他冗余数据而开始表现出性能下降。这不仅会占用宝贵的存储空间,还可能影响设备的响应速度和电池寿命。幸运的是,有多种苹果清理软件…...

vue前端通过sessionStorage缓存字典
正常来说,一个vue项目前端需要用到的一些翻译字典对象保存方式一般有多重, 新建js文件方式保存通过vuex方式保存通过sessionStorage保存通过localStorage保存 正常以上几点的保存方式是够用了。 但是,当有字典不能以文件方式保存并且字典量…...

React Redux使用@reduxjs/toolkit的hooks
关于redux的学习过程需要几个官网,有redux官网,React Redux官网和Redux Toolkit的官网。 其中后者的中文没有找到,不过其中的使用在React Redux官网的快速入门中有介绍。 现在一般不使用connect借接口了。 对于借助Redux Toolkit的React Redu…...

Rejetto HFS 服务器存在严重漏洞受到攻击
AhnLab 报告称 ,黑客正在针对旧版本的 Rejetto HTTP 文件服务器 (HFS) 注入恶意软件和加密货币挖矿程序。 然而,由于存在错误, Rejetto 警告用户不要使用 2.3 至 2.4 版本。 2.3m 版本在个人、小型团队、教育机构和测试网络文件共享的开发…...

Electron开发 - 如何在主进程Main中让node-fetch使用系统代理
背景 开发过程中,用户设置的系统代理是不同的,比如公司内的服务器,所以就要动态地使用系统代理来访问,但是主进程默认为控制台级别的请求,不走系统代理,除非你指定系统代理配置,这个就就有了这…...

vue2 webpack使用optimization.splitChunks分包,实现按需引入,进行首屏加载优化
optimization.splitChunks的具体功能和配置信息可以去网上自行查阅。 这边简单讲一下他的使用场景、作用、如何使用: 1、没用使用splitChunks进行分包之前,所有模块都揉在一个文件里,那么当这个文件足够大、网速又一般的时候,首…...

深入理解 Docker 容器技术
一、引言 在当今的云计算和软件开发领域,Docker 容器技术已经成为了一项不可或缺的工具。它极大地改变了应用程序的部署和运行方式,为开发者和运维人员带来了诸多便利。 二、Docker 容器是什么? Docker 容器是一种轻量级、可移植、自包含的…...

redis并发、穿透、雪崩
Redis如何实现高并发 首先是单线程模型:redis采用单线程可以避免多线程下切换和竞争的开销,提高cpu的利用率,如果是多核cpu,可以部署多个redis实例。基于内存的数据存储:redis将数据存储在内存中,相比于硬…...

【架构设计】-- ACK 机制
1、ACK 机制的定义 ACK(全称:acknowledgement) 机制是一种确认机制,起源于TCP报文到达确认(ACK)机制(参考:TCP报文到达确认(ACK)机制_tcp接收方在收到一个报文…...

这些网络安全知识,请务必牢记!
#网络安全# 随着“互联网”时代的到来,人们的生活变得更加便利,但电信诈骗、信息泄露、恶意软件等也随之而来。面对网络这把双刃剑,如何绷紧思想“安全弦”,正确安全使用网络呢?今天,让我们跟随泰顺网信IP…...

学习笔记——交通安全分析11
目录 前言 当天学习笔记整理 4信控交叉口交通安全分析 结束语 前言 #随着上一轮SPSS学习完成之后,本人又开始了新教材《交通安全分析》的学习 #整理过程不易,喜欢UP就点个免费的关注趴 #本期内容接上一期10笔记 #最近确实太懒了,接受…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
