Python实现傅里叶级数可视化工具
Python实现傅里叶级数可视化工具
flyfish
有matlab实现,我没matlab,我有Python,所以我用Python实现。
整个工具的实现代码放在最后,界面使用PyQt5开发

起源
傅里叶级数(Fourier Series)由法国数学家和物理学家让-巴蒂斯特·约瑟夫·傅里叶(Jean-Baptiste Joseph Fourier)在19世纪初提出。他最初是为了研究热传导问题,发现任何周期函数都可以表示为一系列正弦和余弦函数的和。这一发现对数学、物理学以及工程学等领域产生了深远影响。
思想
傅里叶级数的核心思想是将一个复杂的周期函数分解成无穷多个简单的正弦和余弦函数的叠加。这些正弦和余弦函数称为“基函数”,每个基函数都有特定的频率、幅度和相位。
公式
对于一个周期为 T T T 的周期函数 f ( t ) f(t) f(t),其傅里叶级数表示为: f ( t ) = a 0 + ∑ n = 1 ∞ ( a n cos ( 2 π n t T ) + b n sin ( 2 π n t T ) ) f(t) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos\left(\frac{2\pi n t}{T}\right) + b_n \sin\left(\frac{2\pi n t}{T}\right) \right) f(t)=a0+n=1∑∞(ancos(T2πnt)+bnsin(T2πnt))
其中:
- a 0 a_0 a0 是直流分量(平均值),计算公式为:
a 0 = 1 T ∫ 0 T f ( t ) d t a_0 = \frac{1}{T} \int_{0}^{T} f(t) \, dt a0=T1∫0Tf(t)dt - a n a_n an 和 b n b_n bn 是傅里叶系数,计算公式分别为:
a n = 2 T ∫ 0 T f ( t ) cos ( 2 π n t T ) d t a_n = \frac{2}{T} \int_{0}^{T} f(t) \cos\left(\frac{2\pi n t}{T}\right) \, dt an=T2∫0Tf(t)cos(T2πnt)dt
b n = 2 T ∫ 0 T f ( t ) sin ( 2 π n t T ) d t b_n = \frac{2}{T} \int_{0}^{T} f(t) \sin\left(\frac{2\pi n t}{T}\right) \, dt bn=T2∫0Tf(t)sin(T2πnt)dt
想象一首音乐,这首音乐是由许多不同频率的音符组成的。傅里叶级数就像是一种工具,它可以将这首音乐分解成一个个单独的音符(正弦和余弦函数)。通过这些音符的频率和振幅,可以重建出原来的音乐。
正交函数
在数学中,两个函数 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x) 在定义域 [ a , b ] [a, b] [a,b] 上被称为正交的(orthogonal),如果它们的内积为零。内积通常定义为: ⟨ f , g ⟩ = ∫ a b f ( x ) g ( x ) d x \langle f, g \rangle = \int_a^b f(x) g(x) \, dx ⟨f,g⟩=∫abf(x)g(x)dx当 ⟨ f , g ⟩ = 0 \langle f, g \rangle = 0 ⟨f,g⟩=0 时,表示函数 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x) 在 [ a , b ] [a, b] [a,b] 上是正交的。正交函数有一个重要性质,即它们在某种意义上“互不干扰”。
正交函数集
正交函数集是一组两两正交的函数集合。即对于函数集 { ϕ 1 ( x ) , ϕ 2 ( x ) , … , ϕ n ( x ) } \{ \phi_1(x), \phi_2(x), \ldots, \phi_n(x) \} {ϕ1(x),ϕ2(x),…,ϕn(x)},满足: ⟨ ϕ i , ϕ j ⟩ = ∫ a b ϕ i ( x ) ϕ j ( x ) d x = 0 当 i ≠ j \langle \phi_i, \phi_j \rangle = \int_a^b \phi_i(x) \phi_j(x) \, dx = 0 \quad \text{当 } i \ne j ⟨ϕi,ϕj⟩=∫abϕi(x)ϕj(x)dx=0当 i=j
如果这组函数不仅仅是正交的,并且每个函数的内积等于一个常数(通常为1),则称为正交规范函数集(orthonormal set)。
完备正交函数集
完备正交函数集是一个正交函数集,其中的函数数目足够多,可以表示定义域 [ a , b ] [a, b] [a,b] 上的任意函数。具体来说,任何在该定义域上的平方可积函数(即满足 ∫ a b ∣ f ( x ) ∣ 2 d x < ∞ \int_a^b |f(x)|^2 \, dx < \infty ∫ab∣f(x)∣2dx<∞ 的函数)都可以表示为这个正交函数集的线性组合。用数学语言来说,函数 f ( x ) f(x) f(x) 可以表示为完备正交函数集 { ϕ n ( x ) } \{\phi_n(x)\} {ϕn(x)} 的线性组合: f ( x ) = ∑ n = 1 ∞ c n ϕ n ( x ) f(x) = \sum_{n=1}^{\infty} c_n \phi_n(x) f(x)=∑n=1∞cnϕn(x)其中系数 c n c_n cn 是通过内积计算得到的: c n = ⟨ f , ϕ n ⟩ ⟨ ϕ n , ϕ n ⟩ c_n = \frac{\langle f, \phi_n \rangle}{\langle \phi_n, \phi_n \rangle} cn=⟨ϕn,ϕn⟩⟨f,ϕn⟩
在均方误差为零的情况下,任何与完备正交函数集有相同定义域的函数都可以分解为该函数集中正交函数的代数和
均方误差(Mean Squared Error, MSE)是用来衡量一个函数 f ( x ) f(x) f(x) 与其近似表示 f ^ ( x ) \hat{f}(x) f^(x) 之间的误差的标准。在函数分解中,如果一个函数 f ( x ) f(x) f(x) 可以通过完备正交函数集 { ϕ n ( x ) } \{\phi_n(x)\} {ϕn(x)} 的代数和精确表示,那么均方误差为零。也就是说: MSE = 1 b − a ∫ a b ∣ f ( x ) − f ^ ( x ) ∣ 2 d x = 0 \text{MSE} = \frac{1}{b-a} \int_a^b |f(x) - \hat{f}(x)|^2 \, dx = 0 MSE=b−a1∫ab∣f(x)−f^(x)∣2dx=0当均方误差为零时,表示函数 f ( x ) f(x) f(x) 可以精确地分解为完备正交函数集中的函数的代数和: f ( x ) = ∑ n = 1 ∞ c n ϕ n ( x ) f(x) = \sum_{n=1}^{\infty} c_n \phi_n(x) f(x)=n=1∑∞cnϕn(x)这个结论的意义在于,完备正交函数集提供了一种强大的工具,可以表示定义域 [ a , b ] [a, b] [a,b] 上的任意函数,而不会有任何误差。
解释 展开
傅里叶级数是将一个周期函数展开成一系列正弦函数和余弦函数的和,其基本形式可以表示为:
f ( x ) = a 0 + ∑ n = 1 ∞ ( a n cos ( 2 π n x T ) + b n sin ( 2 π n x T ) ) f(x) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos\left(\frac{2\pi nx}{T}\right) + b_n \sin\left(\frac{2\pi nx}{T}\right) \right) f(x)=a0+n=1∑∞(ancos(T2πnx)+bnsin(T2πnx))
其中, T T T 是周期, a 0 a_0 a0, a n a_n an, b n b_n bn 是傅里叶系数,通过以下公式计算:
a 0 = 1 T ∫ 0 T f ( x ) d x a_0 = \frac{1}{T} \int_{0}^{T} f(x) \, dx a0=T1∫0Tf(x)dx
a n = 2 T ∫ 0 T f ( x ) cos ( 2 π n x T ) d x a_n = \frac{2}{T} \int_{0}^{T} f(x) \cos\left(\frac{2\pi nx}{T}\right) \, dx an=T2∫0Tf(x)cos(T2πnx)dx
b n = 2 T ∫ 0 T f ( x ) sin ( 2 π n x T ) d x b_n = \frac{2}{T} \int_{0}^{T} f(x) \sin\left(\frac{2\pi nx}{T}\right) \, dx bn=T2∫0Tf(x)sin(T2πnx)dx
具体例子:方波函数
方波函数是一个常见的周期函数,可以用傅里叶级数展开。假设我们有一个周期为 T = 2 π T = 2\pi T=2π 的方波函数 f ( x ) f(x) f(x),定义如下: { 1 for 0 < x < π − 1 for π < x < 2 π \begin{cases} 1 & \text{for } 0 < x < \pi \\ -1 & \text{for } \pi < x < 2\pi \end{cases} {1−1for 0<x<πfor π<x<2π
我们将这个函数展开为傅里叶级数。
计算傅里叶系数
- 计算 ( a_0 ):
a 0 = 1 2 π ∫ 0 2 π f ( x ) d x a_0 = \frac{1}{2\pi} \int_{0}^{2\pi} f(x) \, dx a0=2π1∫02πf(x)dx
由于 f ( x ) f(x) f(x)在 [ 0 , π ] [0, \pi] [0,π] 上为 1,在 [ π , 2 π ] [\pi, 2\pi] [π,2π] 上为 -1:
a 0 = 1 2 π ( ∫ 0 π 1 d x + ∫ π 2 π − 1 d x ) a_0 = \frac{1}{2\pi} \left( \int_{0}^{\pi} 1 \, dx + \int_{\pi}^{2\pi} -1 \, dx \right) a0=2π1(∫0π1dx+∫π2π−1dx)
a 0 = 1 2 π ( π − π ) = 0 a_0 = \frac{1}{2\pi} \left( \pi - \pi \right) = 0 a0=2π1(π−π)=0 - 计算 ( a_n ):
a n = 1 π ∫ 0 2 π f ( x ) cos ( n x ) d x a_n = \frac{1}{\pi} \int_{0}^{2\pi} f(x) \cos(nx) \, dx an=π1∫02πf(x)cos(nx)dx
由于 f ( x ) f(x) f(x)是奇函数(关于 x = π x = \pi x=π 对称),且 ( c o s ( n x ) cos(nx) cos(nx)) 是偶函数,奇函数与偶函数的内积为零:
a n = 0 a_n = 0 an=0 - 计算 ( b_n ):
b n = 1 π ∫ 0 2 π f ( x ) sin ( n x ) d x b_n = \frac{1}{\pi} \int_{0}^{2\pi} f(x) \sin(nx) \, dx bn=π1∫02πf(x)sin(nx)dx
同样地,将积分分为两部分:
b n = 1 π ( ∫ 0 π sin ( n x ) d x + ∫ π 2 π − sin ( n x ) d x ) b_n = \frac{1}{\pi} \left( \int_{0}^{\pi} \sin(nx) \, dx + \int_{\pi}^{2\pi} -\sin(nx) \, dx \right) bn=π1(∫0πsin(nx)dx+∫π2π−sin(nx)dx)
由于 s i n ( n x ) sin(nx) sin(nx) 在 [ π , 2 π ] [\pi, 2\pi] [π,2π] 上的负值正好抵消 ( [ 0 , π ] ([0, \pi] ([0,π]上的值:
b n = 1 π ( ∫ 0 π sin ( n x ) d x − ∫ 0 π sin ( n x ) d x ) b_n = \frac{1}{\pi} \left( \int_{0}^{\pi} \sin(nx) \, dx - \int_{0}^{\pi} \sin(nx) \, dx \right) bn=π1(∫0πsin(nx)dx−∫0πsin(nx)dx)
b n = 2 π ∫ 0 π sin ( n x ) d x b_n = \frac{2}{\pi} \int_{0}^{\pi} \sin(nx) \, dx bn=π2∫0πsin(nx)dx
计算这个积分,结果是:
b n = { 4 n π for odd n 0 for even n b_n = \begin{cases} \frac{4}{n\pi} & \text{for odd } n \\ 0 & \text{for even } n \end{cases} bn={nπ40for odd nfor even n
得到傅里叶级数展开
将 ( a_0 ), ( a_n ), ( b_n ) 代入傅里叶级数的基本形式,我们得到方波的傅里叶级数展开:
f ( x ) = ∑ odd n 4 n π sin ( n x ) f(x) = \sum_{\text{odd } n} \frac{4}{n\pi} \sin(nx) f(x)=odd n∑nπ4sin(nx)
具体地,考虑前几项,我们可以写成:
f ( x ) ≈ 4 π sin ( x ) + 4 3 π sin ( 3 x ) + 4 5 π sin ( 5 x ) + … f(x) \approx \frac{4}{\pi} \sin(x) + \frac{4}{3\pi} \sin(3x) + \frac{4}{5\pi} \sin(5x) + \ldots f(x)≈π4sin(x)+3π4sin(3x)+5π4sin(5x)+…
整个工具的代码实现
import sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.backends.backend_qt5agg import FigureCanvasQTAgg as FigureCanvas
from matplotlib.figure import Figure
from mpl_toolkits.mplot3d import Axes3D
from PyQt5.QtWidgets import QApplication, QMainWindow, QWidget, QVBoxLayout, QHBoxLayout, QPushButton, QSlider, QLabel, QLineEdit, QGridLayout
from PyQt5.QtCore import Qtplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseclass FourierSeriesVisualizer(QMainWindow):def __init__(self):super().__init__()self.setWindowTitle("傅里叶级数可视化工具")self.setGeometry(100, 100, 1200, 800)self.central_widget = QWidget(self)self.setCentralWidget(self.central_widget)self.layout = QGridLayout(self.central_widget)# 创建二维图形区self.figure_2d, self.ax_2d = plt.subplots()self.canvas_2d = FigureCanvas(self.figure_2d)self.layout.addWidget(self.canvas_2d, 0, 0)# 创建三维图形区self.figure_3d = Figure()self.ax_3d = self.figure_3d.add_subplot(111, projection='3d')self.canvas_3d = FigureCanvas(self.figure_3d)self.layout.addWidget(self.canvas_3d, 0, 1)# 创建控制面板self.control_panel = QHBoxLayout()self.label_n = QLabel("傅里叶级数次数:", self)self.control_panel.addWidget(self.label_n)self.slider_n = QSlider(Qt.Horizontal, self)self.slider_n.setRange(1, 50)self.slider_n.setValue(10)self.slider_n.valueChanged.connect(self.update_plot)self.control_panel.addWidget(self.slider_n)self.label_custom_n = QLabel("自定义次数:", self)self.control_panel.addWidget(self.label_custom_n)self.input_custom_n = QLineEdit(self)self.input_custom_n.setPlaceholderText("输入次数")self.control_panel.addWidget(self.input_custom_n)self.button_apply = QPushButton("确定", self)self.button_apply.clicked.connect(self.apply_custom_n)self.control_panel.addWidget(self.button_apply)self.button_reset = QPushButton("重置", self)self.button_reset.clicked.connect(self.reset)self.control_panel.addWidget(self.button_reset)self.button_dynamic = QPushButton("查看傅里叶级数动态拟合过程", self)self.button_dynamic.clicked.connect(self.view_dynamic_process)self.control_panel.addWidget(self.button_dynamic)self.layout.addLayout(self.control_panel, 1, 0, 1, 2)# 初始绘图self.update_plot()def compute_fourier_series(self, t, T, N):f_t = np.sign(np.sin(2 * np.pi * t / T))a0 = 2 * np.mean(f_t)an = np.zeros(N)bn = np.zeros(N)for n in range(1, N+1):an[n-1] = 2 * np.mean(f_t * np.cos(2 * np.pi * n * t / T))bn[n-1] = 2 * np.mean(f_t * np.sin(2 * np.pi * n * t / T))return a0, an, bndef reconstruct_signal(self, t, T, a0, an, bn, N):f_reconstructed = a0 / 2for n in range(1, N+1):f_reconstructed += an[n-1] * np.cos(2 * np.pi * n * t / T) + bn[n-1] * np.sin(2 * np.pi * n * t / T)return f_reconstructeddef update_plot(self):N = self.slider_n.value()t = np.linspace(0, 2, 500)T = 2a0, an, bn = self.compute_fourier_series(t, T, N)f_reconstructed = self.reconstruct_signal(t, T, a0, an, bn, N)self.ax_2d.clear()self.ax_2d.plot(t, np.sign(np.sin(2 * np.pi * t / T)), label='原始信号(方波)')self.ax_2d.plot(t, f_reconstructed, label=f'重构信号(傅里叶级数 N={N})')self.ax_2d.set_title('方波的傅里叶级数展开')self.ax_2d.set_xlabel('时间')self.ax_2d.set_ylabel('幅度')self.ax_2d.legend()self.ax_2d.grid(True)self.ax_2d.set_ylim(-1.5, 1.5)self.canvas_2d.draw()self.update_3d_plot(a0, an, bn, N, T)def update_3d_plot(self, a0, an, bn, N, T):t = np.linspace(0, 2, 500)f_reconstructed = self.reconstruct_signal(t, T, a0, an, bn, N)self.ax_3d.clear()self.ax_3d.plot(t, f_reconstructed, zs=0, zdir='y', label='重构信号', color='b')for n in range(1, N+1):component = an[n-1] * np.cos(2 * np.pi * n * t / T) + bn[n-1] * np.sin(2 * np.pi * n * t / T)self.ax_3d.plot(t, component, zs=n, zdir='y', label=f'谐波 {n}')self.ax_3d.set_xlabel('时间')self.ax_3d.set_ylabel('谐波')self.ax_3d.set_zlabel('幅度')self.ax_3d.legend(loc='upper left')self.canvas_3d.draw()def apply_custom_n(self):try:custom_n = int(self.input_custom_n.text())if custom_n > 0:self.slider_n.setValue(custom_n)except ValueError:passdef reset(self):self.slider_n.setValue(10)self.input_custom_n.clear()def view_dynamic_process(self):for n in range(1, self.slider_n.value() + 1):self.slider_n.setValue(n)QApplication.processEvents()self.update_plot()if __name__ == "__main__":app = QApplication(sys.argv)main_window = FourierSeriesVisualizer()main_window.show()sys.exit(app.exec_())相关文章:

Python实现傅里叶级数可视化工具
Python实现傅里叶级数可视化工具 flyfish 有matlab实现,我没matlab,我有Python,所以我用Python实现。 整个工具的实现代码放在最后,界面使用PyQt5开发 起源 傅里叶级数(Fourier Series)由法国数学家和物理学家让-巴…...

PDF 分割拆分 API 数据接口
PDF 分割拆分 API 数据接口 文件处理,PDF 高效的 PDF 分割工具,高效处理,可永久存储。 1. 产品功能 高效处理大文件;支持多语言字符识别;支持 formdata 格式 PDF 文件流传参;支持设置每个 PDF 文件的页数…...

【python】随机森林预测汽车销售
目录 引言 1. 数据收集与预处理 2. 划分数据集 3. 构建随机森林模型 4. 模型训练 5. 模型评估 6. 模型调优 数据集 代码及结果 独热编码 随机森林模型训练 特征重要性图 混淆矩阵 ROC曲线 引言 随机森林(Random Forest)是一种集成学习方法…...

Stable Diffusion教程|练丹师是如何炼丹的Lora模型训练
前言 还记得我们之前就讲过学习SD成为炼丹师不?那么今天就来手把手教大家炼丹,看看同一个角色或某种风格的小模型是如何制作出来的。 目录 1 炼丹介绍 2 环境准备 3 Lora模型训练 **一、**炼丹介绍 什么是炼丹? 早在学习SD地第一篇就…...

QT--SQLite
配置类相关的表,所以我使用sqlite,且QT自带该组件; 1.安装 sqlite-tools-win-x64-3460000、SQLiteExpert5.4.31.575 使用SQLiteExpert建好数据库.db文件,和对应的表后把db文件放在指定目录 ./db/program.db; 2.选择sql组件 3.新…...

【深度学习入门篇 ②】Pytorch完成线性回归!
🍊嗨,大家好,我是小森( ﹡ˆoˆ﹡ )! 易编橙终身成长社群创始团队嘉宾,橙似锦计划领衔成员、阿里云专家博主、腾讯云内容共创官、CSDN人工智能领域优质创作者 。 易编橙:一个帮助编程小…...

Syslog 管理工具
Syslog常被称为系统日志或系统记录,是一种用来在互联网协议(TCP/IP)的网上中传递记录档消息的标准,常用来指涉实际的Syslog 协议,或者那些提交syslog消息的应用程序或数据库。 系统日志协议(Syslog&#x…...

硅纪元AI应用推荐 | 百度橙篇成新宠,能写万字长文
“硅纪元AI应用推荐”栏目,为您精选最新、最实用的人工智能应用,无论您是AI发烧友还是新手,都能在这里找到提升生活和工作的利器。与我们一起探索AI的无限可能,开启智慧新时代! 百度橙篇,作为百度公司在202…...

Codeforces Round 954 (Div. 3)
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,彩笔ACMer一枚。 🏀所属专栏:Codeforces 本文用于记录回顾本彩笔的解题思路便于加深理解。 📢📢📢传送阵 A. X Axis解…...

【Django】报错‘staticfiles‘ is not a registered tag library
错误截图 错误原因总结 在django3.x版本中staticfiles被static替换了,所以这地方换位static即可完美运行 错误解决...
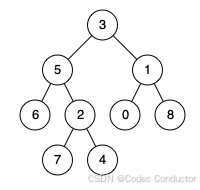
LeetCode 算法:二叉树的最近公共祖先 III c++
原题链接🔗:二叉树的最近公共祖先 难度:中等⭐️⭐️ 题目 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点…...

Windows CMD 命令汇总表
Windows CMD 命令汇总表 Windows CMD 命令汇总表目录操作磁盘操作文件操作其他命令FTP 命令高级系统命令批处理命令网络命令安全和权限命令 Windows CMD 命令指南目录操作MD - 创建子目录CD - 切换当前目录RD - 删除子目录DIR - 显示目录内容PATH - 设置可执行文件的搜索路径TR…...

【python+appium】自动化测试
pythonappium自动化测试系列就要告一段落了,本篇博客咱们做个小结。 首先想要说明一下,APP自动化测试可能很多公司不用,但也是大部分自动化测试工程师、高级测试工程师岗位招聘信息上要求的,所以为了更好的待遇,我们还…...
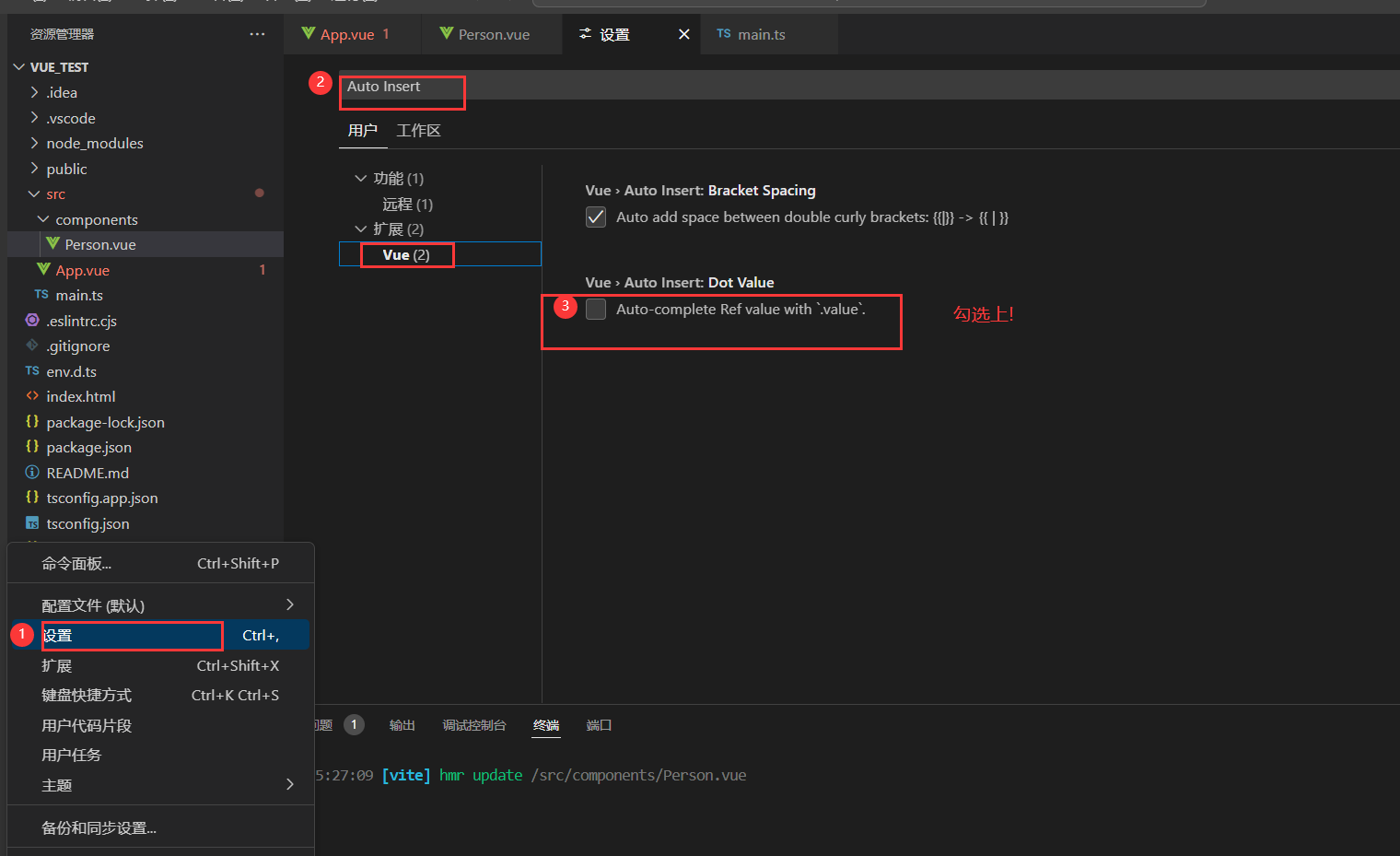
vue 数据类型
文章目录 ref 创建:基本类型的响应式数据reactive 创建:对象类型的响应式数据ref 创建:对象类型的响应式数据ref 对比 reactive将一个响应式对象中的每一个属性,转换为ref对象(toRefs 与 toRef)computed (根据计算进行修改) ref 创…...
)
MySQL(基础篇)
DDL (Data Definition Language) 数据定义语言,用来定义数据库对象(数据库,表, 字段) DML (Data Manipulation Languag) 数据操作语言,用来对数据库表中的数据进行增删改 DQL (Data Query Language) 数据查询语言,用…...
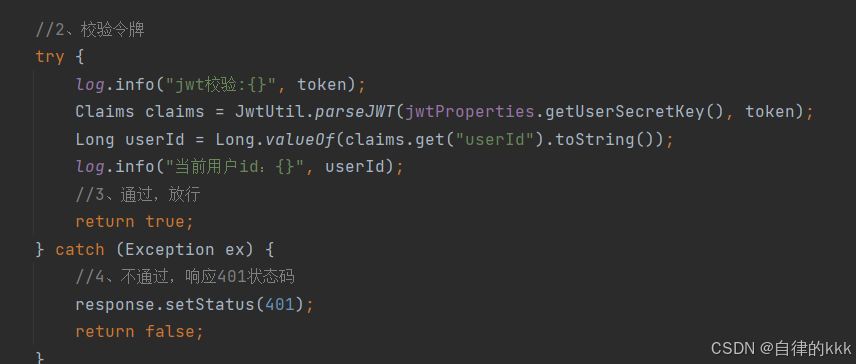
springboot中通过jwt令牌校验以及前端token请求头进行登录拦截实战
前言 大家从b站大学学习的项目侧重点好像都在基础功能的实现上,反而一个项目最根本的登录拦截请求接口都不会写,怎么拦截?为什么拦截?只知道用户登录时我后端会返回一个token,这个token是怎么生成的,我把它…...

从零开始开发视频美颜SDK:实现直播美颜效果
因此,开发一款从零开始的视频美颜SDK,不仅可以节省成本,还能根据具体需求进行个性化调整。本文将介绍从零开始开发视频美颜SDK的关键步骤和实现思路。 一、需求分析与技术选型 在开发一款视频美颜SDK之前,首先需要进行详细的需求…...

极验语序点选验证码识别(一)
注意,本文只提供学习的思路,严禁违反法律以及破坏信息系统等行为,本文只提供思路 极验文字点选验证码不必多说,很多小伙伴,借助标注工具或者打码平台标注完数据集后,使用开源的目标检测网络即可完成,欢迎收看我之前的文章: Pytorch利用ddddocr辅助识别点选验证码 或者使…...
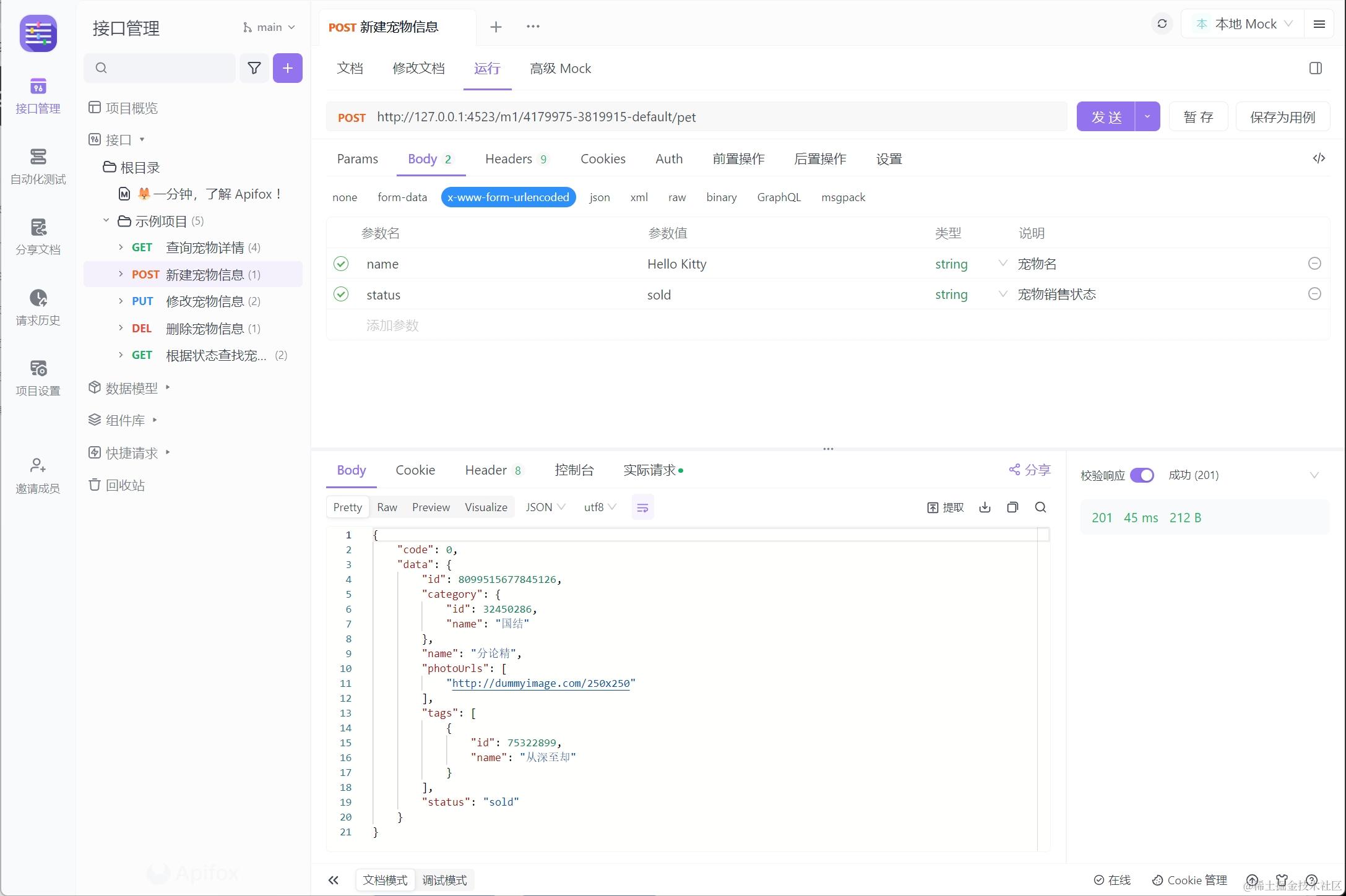
什么是 HTTP POST 请求?初学者指南与示范
在现代网络开发领域,理解并应用 HTTP 请求 方法是基本的要求,其中 "POST" 方法扮演着关键角色。 理解 POST 方法 POST 方法属于 HTTP 协议的一部分,主旨在于向服务器发送数据以执行资源的创建或更新。它与 GET 方法区分开来&…...
第一次作业
任务需求:1.DMz区内的服务器,办公区仅能在办公时间内(9-18)可以访问,生产区的设备全天可以访问 2.生产区不允许访问互联网,办公区和游客区可以访问互联网 3.办公区设备10.0.2.10不允许访问DMZ区的FTP服务器和http服务器,仅能ping通…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
