算法学习day10(贪心算法)
贪心算法:由局部最优->全局最优
贪心算法一般分为如下四步:
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
一、摆动序列(理解难)
连续数字之间的差有正负的交替,则序列称为摆动序列。返回的nums值是摆动序列中元素的个数
-
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。 
思路:将数组想象成一个上上下下的图表,定义curDiff=nums[i]-nums[i-1];和preDiff=nums[i+1]-nums[i];
考虑数组两端 : 假设在数组开头元素再添加一个相同的元素(或者初始化preDiff==0),这样在遍历第一个元素的时候,就不会发生数组越界问题。if(preDiff>=0&&curDiff<0||preDiff<=0&&curDiff>0)
前者对应的是先上再下,后者对应的是先下(可能为平坡)再上
考虑到末尾元素,直接让result=1(默认最右边有一个峰值)
单调坡度有平坡:

不是每一次遍历都要更新preDiff的值,而是当遇到峰值,前后波动的时候才去更新preDiff的值(为什么?);
代码:
class Solution {public int wiggleMaxLength(int[] nums) {// 根据nums的长度剪枝if (nums.length <= 1)return nums.length;// 定义preDiff 和 curDiff 根据循环加resultint preDiff = 0;int curDiff = 0;int result = 1;// 把最后的元素看成一个峰值 直接+1for (int i = 0; i < nums.length - 1; i++) {curDiff = nums[i + 1] - nums[i];if (preDiff <= 0 && curDiff > 0 || preDiff >= 0 && curDiff < 0) {result++;// 遇到峰值 前后波动preDiff = curDiff;}}return result;}
}二、最大子序和(贪心法/dp)
贪心法:
由局部最优推导出全局最优:连续和变为负数,下一个元素就不要加连续和。连续和为正数再加。
count+=nums[i] if(count>result)result=count; if(count<0)count=0;
代码:
public int maxSubArray(int[] nums) {int result=Integer.MIN_VALUE;int count=0;for(int i=0;i<nums.length;i++){count+=nums[i];if(count>result)result=count;if(count<0)count=0;}return result;}Dp(动态规划):
dp[i]:表示以从0->i这段集合的最大值。
dp[i]=Math.max(dp[i-1]+nums[i],nums[i])。eg:以3为下标,如果dp[2]为负数那肯定不加,加上拖后腿。如果dp[i-1]为正数,那肯定加。
代码:
class Solution {public int maxSubArray(int[] nums) {int ans = Integer.MIN_VALUE;int[] dp = new int[nums.length];//dp[0]和nums[0]相等dp[0] = nums[0];ans = dp[0];for (int i = 1; i < nums.length; i++){dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);ans = Math.max(dp[i], ans);}return ans;}
}三、买卖股票的最佳时机(一次遍历)
暴力法搜索的话会超时异常
所以使用一次遍历:每次遍历到下标为i的元素时,就更新minprice。然后计算出在该天卖出,可以赚多少钱。
之前的思想是:如果在今天买,什么时候卖可以赚更多的钱。
现在的思想:如果今天卖,什么时候买可以赚更多钱。那我们就计算出今天之前的最小值,然后在那天买,今天卖,就可以找出最大利润。
代码:
class Solution {public int maxProfit(int[] prices) {int minprice = Integer.MAX_VALUE;int maxprofit = 0;for (int i = 0; i < prices.length; i++) {if (prices[i] < minprice) {minprice = prices[i];} else if (prices[i] - minprice > maxprofit) {maxprofit = prices[i] - minprice;}}return maxprofit;}
}
四、买卖股票的最佳时机II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。返回 你能获得的 最大 利润。
要求最大利润->就要求从第二天开始每一天的利润。
局部利润最大->全局利润最大
代码:
class Solution {public int maxProfit(int[] prices) {int sumProfit=0;for(int i=1;i<prices.length;i++){if(prices[i]-prices[i-1]>0){sumProfit+=prices[i]-prices[i-1];}}return sumProfit;}
}五、跳跃游戏(回溯/贪心)
回溯法:
宽度为nums[i]的大小,表示可以最大跳多远。for(int i=1;i<=nums[i]);i++)
深度就是跳到最后一个元素所经历的节点个数。
返回值:boolean;参数:int[] nums,int startIndex,boolean[] used
终止条件:当startIndex==nums.length-1的时候,代表已经跳到了最后一个元素。如果>的话就跳超了,直接return false;
单层递归逻辑:
1.首先判断该点是不是遇到过(去重)if(used[startIndex]==true)return false;
2.然后使用一个boolean的变量接收下一层遍历的返回值,如果下一层返回true,那么这一层也返回true。如果下一层返回false,说明下一个不行,直接used[i+startIndex]=true
代码:
class Solution {public boolean canJump(int[] nums) {if (nums.length == 1)return true;// 只有一个元素的时候boolean[] used = new boolean[nums.length];return backTracking(nums, 0, used);}public boolean backTracking(int[] nums, int startIndex, boolean[] used) {if (startIndex == nums.length - 1)return true;if (startIndex > nums.length - 1)return false;if (used[startIndex])return false;// 之前已经来过这个下标位置 已经试过这种情况了 就直接返回falsefor (int i = 1; i <= nums[startIndex]; i++) {boolean flag = backTracking(nums, startIndex + i, used);if (flag == true) {return true;} else {used[startIndex + i] = true;}}used[startIndex] = true;return false;}
}贪心法:
将跳跃问题->范围覆盖问题,如果在某点上,位置覆盖到nums.length-1,那么就说明可以跳到最后一个位置,返回true;
在每次coverRange的范围里面,去更新coverRange的范围。coverRange=Math.max(coverRange,i+nums[i]);
if(coverRange>=nums.length-1)。为什么是>=而不是==。因为如果是>=的话,最后一个节点在我跳跃的范围里面。
代码:
class Solution {public boolean canJump(int[] nums) {if(nums.length==1)return true;int coverRange=0;//覆盖的范围是元素的下标 所以下面的for循环可以使用=for(int i=0;i<=coverRange;i++){coverRange=Math.max(coverRange,i+nums[i]);if(coverRange>=nums.length-1)return true;}return false;}
}六、跳跃游戏II(贪心)在上一道题的基础上求最小跳跃次数
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
思路:整体最优解:在一个范围里面,每次都往最远的跳。方式:在0->cur这个范围里面,找到下一次可以跳跃到的最远距离,next=Math.max(next,i+nums[i]);
如果cur!=nums.length-1,说明还没有到达终点,那我们就要cur=next(改变范围),并且result++
如果next==nums.length,result++然后跳
代码:
class Solution {public int jump(int[] nums) {if(nums.length<=1)return 0;// 定义变量 cur next resultint cur = 0, next = 0, result = 0;for (int i = 0; i < nums.length; i++) {// 每次都更新一个范围里下次能跳到的最远距离next = Math.max(i + nums[i], next);if(next>=nums.length-1){result++;break;} if(i==cur){result++;cur=next;}}return result;}
}七、K次取反后最大化的数组和
贪心策略的选择:
1.如果有负数的话,先对绝对值更大的负数进行取反,直到k为0;
2.如果所有的负数都取反完后,k不为0并且为奇数,就对最小的非负数进行取反。如果k为偶数,不用变。
注意:将数组从小到大排序之后,负数取反的值可能比之前的正数小,所以在取反并且k!=0后,要将数组再次排序。
代码:
class Solution {public int largestSumAfterKNegations(int[] nums, int k) {Arrays.sort(nums);//先对nums进行排序int startK=k;for(int i=0;i<nums.length;i++){if(nums[i]<0&&k>0){nums[i]*=-1;k--;}}//如果k不为0并且k为一个奇数,就选择一个最小的正数去抵消它if(k%2!=0){Arrays.sort(nums);nums[0]*=-1;}return sumOfArr(nums);}public int sumOfArr(int[] nums){int sum=0;for(int i:nums){sum+=i;}return sum;}
}八、加油站(贪心)
卡尔哥的思路:一个加油站可以a升,但是去下一个加油站要消耗b升,一个加油站可以获取/消耗的油为(a-b),
1.使用变量curSum将它们累加起来,如果curSum<0,就说明汽油不够到达下一个加油站。那么此时将curSum置为零(i也会从下一个开始),
2.再使用一个变量totalSum将所有加油站的盈余都加起来,如果<0,就说明无论从哪一个起点开始都无法回到起点。
代码:
class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {int gasSum=0;int totalSum=0;int index=0;for(int i=0;i<gas.length;i++){gasSum+=gas[i]-cost[i];//当前的累积量 如果<0 说明以i为起点的 无法循环totalSum+=gas[i]-cost[i];//总的累积量 如果<0 绝对找不到一个起点if(gasSum<0){index=(i+1)%gas.length;gasSum=0;}}if(totalSum<0)return -1;return index;}
}九、分发糖果(贪心法)
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
问题:一个孩子所分发的糖果是由两边人共同影响的。eg:2 5 3 2 。所分的糖果为1,2 但是第三个位置就不知道怎么确定了。
思路:先从左边遍历,再从右边遍历,遍历到相同的位置要取最大值(因为同时要满足两个)
代码:
class Solution {public int candy(int[] ratings) {int[] candies=new int[ratings.length];//首先我们从左往右遍历candies[0]=1;for(int i=1;i<ratings.length;i++){if(ratings[i]>ratings[i-1])candies[i]=candies[i-1]+1;else candies[i]=1;}//我们从右往左遍历for(int i=ratings.length-2;i>=0;i--){if(ratings[i]>ratings[i+1]){candies[i]=Math.max(candies[i],candies[i+1]+1);}}return sumOfArr(candies);}public int sumOfArr(int[] candies){int sum=0;for(int i:candies){sum+=i;}return sum;}
}十、柠檬水找零(暴力)
暴力法:对bills[i]进行分情况判断,==5/==10/==20。使用一个map集合当做钱包
1.等于5的时候,直接往map集合中添加
2.等于10的时候,先判断5的是否>=1,然后更新一下5和10的数量
3.等于20的时候,优先使用5和10的进行支付,然后选择三个5的进行支付。(因为5还要去支付10的)
代码:
class Solution {public boolean lemonadeChange(int[] bills) {//使用一个map集合存钱Map<Integer, Integer> map = new HashMap();map.put(5,0);map.put(10,0);for (int i = 0; i < bills.length; i++) {if (bills[i] == 5) map.put(5, map.get(5) + 1);else if (bills[i] == 10) {if (map.get(5) >= 1) {map.put(5, map.get(5) - 1);map.put(10, map.get(10) + 1);} else {return false;}} else if (bills[i] == 20) {if(map.get(10)>0&&map.get(5)>0){map.put(10,map.get(10)-1);map.put(5,map.get(5)-1);}else if(map.get(5)>=3){map.put(5,map.get(5)-3);}else{return false;}}}return true;}
}十一、根据身高重建队列(贪心)
Arrays.sort()函数中可以自定义一个comparator规则,一般使用Lambda表达式简化书写(我感觉可读性不高)。
 匿名内部类:(当我们只需要用一次的时候,就不需要再创建一个类,而是通过匿名内部类来实现)
匿名内部类:(当我们只需要用一次的时候,就不需要再创建一个类,而是通过匿名内部类来实现)
例如:
public class Demo {public static void main(String[] args) {//创建匿名内部类,直接重写父类的方法,省去了创建子类继承,创建子类对象的过程Fu fu= new Fu(){@Overridepublic void method() { //重写父类method方法super.method();}};fu.method(); //调用method方法}思路:将people[][]二维数组,通过Arrays.sort()排序。排序规则为:根据身高h排,即people[i][0]。
如果身高相等那么,根据前面的人:people[i][1]来排,升序排
第一种是普通的写法/第二种是使用lambda表达式简化开发
Arrays.sort(people, new Comparator<int[]>() {@Overridepublic int compare(int[] o1, int[] o2) {if(o1[0]==o2[0])return o1[1]-o2[1];return o2[0]-o1[0];}}); Arrays.sort(people,((o1, o2) -> {if(o1[0]==o2[0])return o2[1]-o2[0];return o2[0]-o1[0];//降序排}));排序好之后,根据people[i][k]来进行排序,k为多少就插到下标为多少的位置。
java中的集合直接封装好了add(int index,T element)方法;
add(peo[1],peo);
代码:
public int[][] reconstructQueue(int[][] people) {Arrays.sort(people,(a,b)->{if(a[0]==b[0])return a[1]-b[1];//如果身高相同 就比k k越小应该在越前面 所以是a-breturn b[0]-a[0];//降序排 是b-a});LinkedList<int[]> queue=new LinkedList<>();for(int[] peo:people){queue.add(peo[1],peo);}return queue.toArray(new int[people.length][]);}相关文章:

算法学习day10(贪心算法)
贪心算法:由局部最优->全局最优 贪心算法一般分为如下四步: 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解 一、摆动序列(理解难) 连续数字之间的差有正负的交替&…...
卡尔曼滤波Kalman Filter零基础入门到实践(上部)
参考视频:入门(秒懂滤波概要)_哔哩哔哩_bilibili 一、入门 1.引入 假设超声波距离传感器每1ms给单片机发数据。 理论数据为黑点, 测量数据曲线为红线,引入滤波后的数据为紫线 引入滤波的作用是过滤数据中的噪声&a…...
力扣-dfs
何为深度优先搜索算法? 深度优先搜索算法,即DFS。就是找一个点,往下搜索,搜索到尽头再折回,走下一个路口。 695.岛屿的最大面积 695. 岛屿的最大面积 题目 给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相…...

keepalived高可用集群
一、keepalived: 1.keepalive是lvs集群中的高可用架构,只是针对调度器的高可用,基于vrrp来实现调度器的主和备,也就是高可用的HA架构;设置一台主调度器和一台备调度器,在主调度器正常工作的时候࿰…...

文献翻译与阅读《Integration Approaches for Heterogeneous Big Data: A Survey》
CYBERNETICS AND INFORMATION TECHNOLOGIES’24 论文原文下载地址:原文下载 目录 1 引言 2 大数据概述 3 大数据的异构性 4 讨论整合方法 4.1 大数据仓库(BDW) 4.2 大数据联盟(BDF) 5 DW 和 DF 方法的比较、分…...

应用最优化方法及MATLAB实现——第3章代码实现
一、概述 在阅读最优方法及MATLAB实现后,想着将书中提供的代码自己手敲一遍,来提高自己对书中内容理解程度,巩固一下。 这部分内容主要针对第3章的内容,将其所有代码实现均手敲一遍,中间部分代码自己根据其公式有些许的…...

django的增删改查,排序,分组等常用的ORM操作
Django 的 ORM(对象关系映射)提供了一种方便的方式来与数据库进行交互。 1. Django模型 在 myapp/models.py 中定义一个示例模型:python from django.db import modelsclass Person(models.Model):name models.CharField(max_length100)age…...

Leetcode Java学习记录——树、二叉树、二叉搜索树
文章目录 树的定义树的遍历中序遍历代码 二叉搜索树 常见二维数据结构:树/图 树和图的区别就在于有没有环。 树的定义 public class TreeNode{public int val;public TreeNode left,right;public TreeNode(int val){this.val val;this.left null;this.right nu…...

华为HCIP Datacom H12-821 卷30
1.单选题 以下关于OSPF协议报文说法错误的是? A、OSPF报文采用UDP报文封装并且端口号是89 B、OSPF所有报文的头部格式相同 C、OSPF协议使用五种报文完成路由信息的传递 D、OSPF所有报文头部都携带了Router-ID字段 正确答案:A 解析: OSPF用IP报文直接封装协议报文,…...
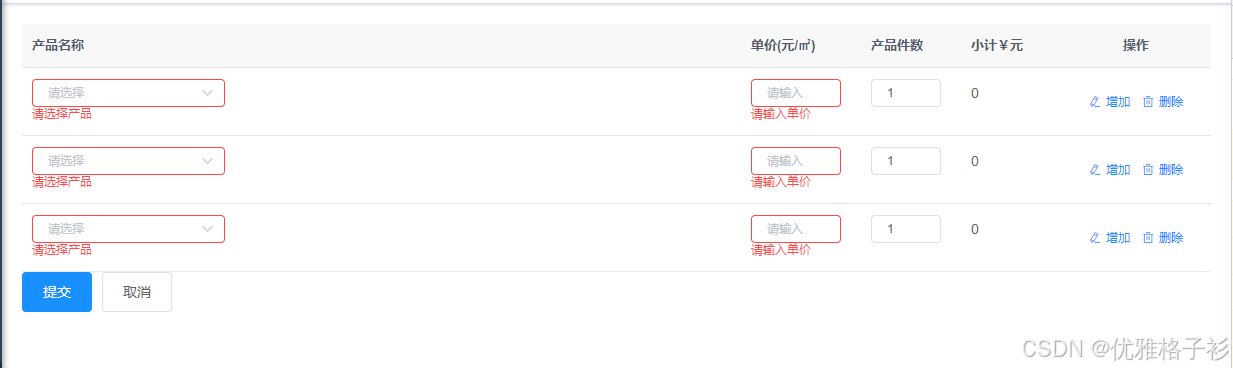
element el-table实现表格动态增加/删除/编辑表格行,带校验规则
本篇文章记录el-table增加一行可编辑的数据列,进行增删改。 1.增加空白行 直接在页面mounted时对form里面的table列表增加一行数据,直接使用push() 方法增加一列数据这个时候也可以设置一些默认值。比如案例里面的 产品件数 。 mounted() {this.$nextTi…...

QT调节屏幕亮度
1、目标 利用QT实现调节屏幕亮度功能:在无屏幕无触控时,将屏幕亮度调低,若有触控则调到最亮。 2、调节亮度命令 目标装置使用嵌入式Linux系统,调节屏幕亮度的指令为: echo x > /sys/class/backlight/backlight/…...

实变函数精解【3】
文章目录 点集求导集 闭集参考文献 点集 求导集 例1 E { 1 / n 1 / m : n , m ∈ N } 1. lim n → ∞ ( 1 / n 1 / m ) 1 / m 2. lim n , m → ∞ ( 1 / n 1 / m ) 0 3. E ′ { 0 , 1 , 1 / 2 , 1 / 3 , . . . . } E\{1/n1/m:n,m \in N\} \\1.\lim_{n \rightar…...

JVM:SpringBoot TomcatEmbeddedWebappClassLoader
文章目录 一、介绍二、SpringBoot中TomcatEmbeddedWebappClassLoader与LaunchedURLClassLoader的关系 一、介绍 TomcatEmbeddedWebappClassLoader 是 Spring Boot 在其内嵌 Tomcat 容器中使用的一个类加载器(ClassLoader)。在 Spring Boot 应用中&#…...
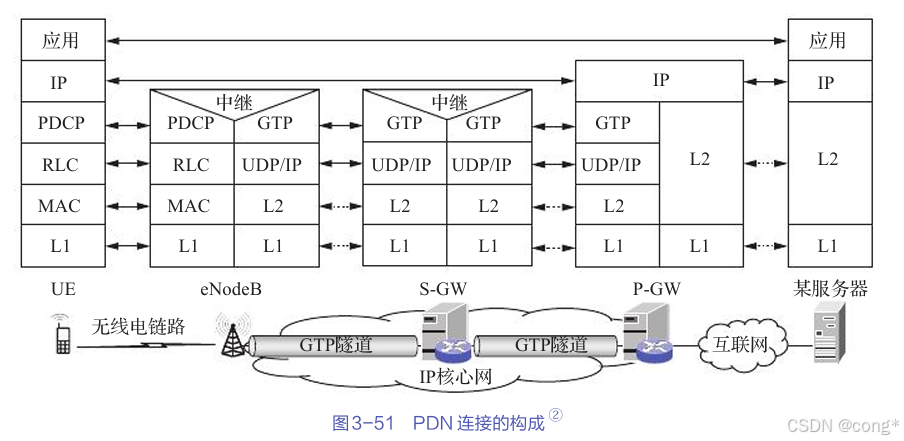
蜂窝互联网接入:连接世界的无缝体验
通过Wi—Fi,人们可以方便地接入互联网,但无线局域网的覆盖范围通常只有10~100m。当我们携带笔记本电脑在外面四处移动时,并不是在所有地方都能找到可接入互联网的Wi—Fi热点,这时候蜂窝移动通信系统可以为我们提供广域…...

Sprint Boot 2 核心功能(一)
核心功能 1、配置文件 application.properties 同基础入门篇的application.properties用法一样 Spring Boot 2 入门基础 application.yaml(或application.yml) 基本语法 key: value;kv之间有空格大小写敏感使用缩进表示层级关系缩进不允…...
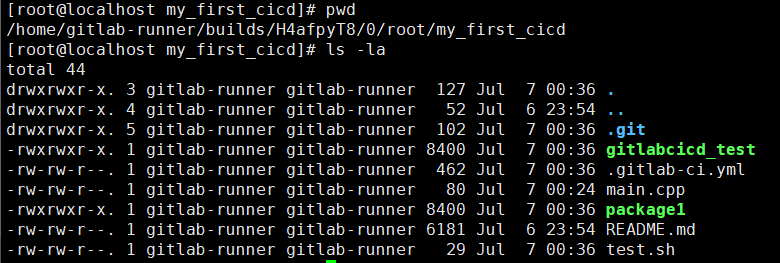
GitLab CI/CD实现项目自动化部署
1 GitLab CI/CD介绍 GitLab CI/CD 是 GitLab 中集成的一套用于软件开发的持续集成(Continuous Integration)、持续交付(Continuous Delivery)和持续部署(Continuous Deployment)工具。这套系统允许开发团队…...

阿里云调整全球布局关停澳洲云服务器,澳洲服务器市场如何选择稳定可靠的云服务?
近日,阿里云宣布将关停澳大利亚地域的数据中心服务,这一决定引发了全球云计算行业的广泛关注。作为阿里云的重要海外市场之一,澳洲的数据中心下架对于当地的企业和个人用户来说无疑是一个不小的挑战。那么,在阿里云调整全球布局的…...
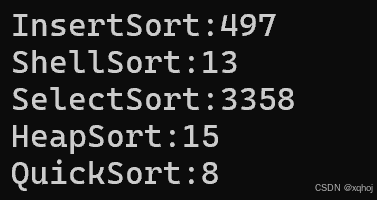
排序(二)——快速排序(QuickSort)
欢迎来到繁星的CSDN,本期内容包括快速排序(QuickSort)的递归版本和非递归版本以及优化。 一、快速排序的来历 快速排序又称Hoare排序,由霍尔 (Sir Charles Antony Richard Hoare) ,一位英国计算机科学家发明。霍尔本人是在发现冒泡排序不够快…...
<数据集>穿越火线cf人物识别数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:3440张 标注数量(xml文件个数):3440 标注数量(txt文件个数):3440 标注类别数:1 标注类别名称:[person] 使用标注工具:labelImg 标注规则:对…...

a+=1和a=a+1的区别
文章目录 a1 和a a1的区别一、实例代码二、代码解释三、总结 a1 和a a1的区别 一、实例代码 public class Test {public static void main(String[] args) {byte a 10; // a a 1; // a (byte) (a 1);a 1;System.out.println(a);} }上面的对变量a进行加一操作时&a…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
