算法学习day12(动态规划)
一、不同的二叉搜索树
二叉搜索树的性质:父节点比左边的孩子节点都大;比右边的孩子节点都小;


由图片可知,dp[3]是可以由dp[2]和dp[1]得出来的。(二叉搜索树的种类和根节点的val有关)
当val为1时,左边是一定没有节点的,因为左边的值都要比根节点小;
只有右边会有n-val个节点。所以当val=1时,dp[i]=dp[i-val]*dp[val-1];
当val=n时候,左边的叶子结点有n-1,右边的节点有i-n;dp[i]=dp[i-val]*dp[val-1];
1.dp[i]:当节点为i的时候,有多少种二叉搜索树
2.关系递推式:dp[i]=dp[val-1]*dp[i-val];
3.初始化:dp[0]=1(空树) dp[1]=dp[1-1]*dp[1-1]=1
4.遍历顺序:从1开始
代码:
public int numTrees(int n) {int[] dp=new int[n+1];//初始化dp[0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){dp[i]+=dp[j-1]*dp[i-j];}}return dp[n];}二、背包问题
01背包:n种物品,每种物品只有一个
完全背包:n种物品,每种物品有无限个
多重背包:n种物品,每种物品有不同个
01背包:
1.dp[i][j]数组的含义:i代表物品,j代表容量。dp[x][y],在容量为y的前提下,选择0-x号物品,所获得的最大价值。
2.递推公式:dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
3.dp数组初始化:
3.1 j=0,表示容量为0,因此dp[x][0]=0;
3.2 i=0,表示物品只能选择第一个,只有容量>=weight[0]的时候,dp[0][weight[0]]才有值
4.遍历顺序:两层for循环,先是商品也可以先是容量也可以
5.打印数组
三、背包问题之滚动数组(将二维数组压缩为一维数组)
1.dp[j]:j是背包容量。dp[j]代表:当背包容量为j时,价值最大为多少?
2.dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i]);
3.dp数组初始化:都初始为0
4.遍历顺序:先遍历物品,再遍历容量,并且容量倒序遍历(保证物品i只被添加一次。)
(只能先物品再容量)
5.打印数组
代码:
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){int wLen = weight.length;//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值int[] dp = new int[bagWeight + 1];//遍历顺序:先遍历物品,再遍历背包容量for (int i = 0; i < wLen; i++){for (int j = bagWeight; j >= weight[i]; j--){dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}//打印dp数组for (int j = 0; j <= bagWeight; j++){System.out.print(dp[j] + " ");}四、分割等和子集(回溯法/动态规划)
给定一个非空的正整数数组 nums ,请判断能否将这些数字分成元素和相等的两部分。
一、回溯法:
private List<Integer> list = new ArrayList<>();public boolean canPartition(int[] nums) {int sum=0;for(int i:nums){sum+=i;}if(sum%2!=0)return false;return backTracking(nums, 0, sum/2);}public boolean backTracking(int[] nums, int startIndex, int target) {if (sumOfList(list) == target)return true;if (sumOfList(list) > target||startIndex>=nums.length)return false;for (int i = startIndex; i < nums.length; i++) {boolean flag = backTracking(nums, i+1, target-nums[i]);if (flag == true)return true;}return false;}public int sumOfList(List<Integer> list) {int sum = 0;for (int i : list) {sum += i;}return sum;}二、动态规划:
这道题的关键在于:把数字的重量和价值都当做数值,在(num.length-1)个物品中,容量为target,选取价值为target的物品
判断条件为dp[nums.length-1][target]==target
1.dp[i][j]:和背包问题一样的含义
2.dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
3.初始化:默认对二维数组所有元素都初始为0,第一行需要改一下,当j>=nums[0]的时候,dp[0][j]=nums[0]
4.遍历顺序i=1,j=0;有一个判断条件:当剩余容量小于物品的重量时,直接下一个
if(j<nums[i])dp[i][j]=dp[i-1][j];
代码:
public boolean canPartition(int[] nums) {int sum = 0;for (int i : nums) {sum += i;}if (sum % 2 != 0)return false;int target = sum / 2;// 定义dp数组int[][] dp = new int[nums.length][target + 1];// 对dp数组进行初始化for (int i = nums[0]; i <= target; i++) {dp[0][i] = nums[0];}// 遍历dp数组for (int i = 1; i < nums.length; i++) {for (int j = 0; j < target + 1; j++) {if (j < nums[i]) {dp[i][j] = dp[i - 1][j];} else{dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);}}}//相当于 物品的个数为nums.length-1中,容量为target,选取价值为target的物品return dp[nums.length-1][target]==target;}五、最后一块石头的重量II(类似分割等和子集)
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
思路:将一堆石头分成两堆,使他们的总重量接近。仍然使用dp数组,这里使用一维dp数组
1.dp[j]:j表示背包的容量.dp[j]表示该容量下的最大价值
2.dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
3.初始化
4.遍历
代码:
//我要在这么多石头里面 容量为x 要实现价值最高
class Solution {public int lastStoneWeightII(int[] stones) {// 定义dp数组int sum=0;for(int i:stones){sum+=i;}int[] dp=new int[sum/2+1];//容量为sum/2+1的数组// 遍历for(int i=0;i<stones.length;i++){for(int j=sum/2;j>=0;j--){if(j>=stones[i]){dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);}}}return sum-dp[sum/2]-dp[sum/2];}
}六、目标和(回溯/动态规划)
给定一个正整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1" - 返回可以通过上述方法构造的、运算结果等于
target的不同 表达式 的数目。
一、回溯法
二叉树的宽度是每次选正还是选负,二叉树的深度是数组的大小
三部曲:
1.返回值:void; 参数:int[] nums,int target,int startIndex(数组的下标)
2.终止条件:当startIndex==nums.length(说明最后一个元素已经遍历完了)
if(sum==target)count++;
3.单层递归逻辑:本层for循环中,要遍历+/- nums[i],还要回溯
class Solution {public int sum = 0;public int count = 0;public int findTargetSumWays(int[] nums, int target) {backTracking(nums, target, 0);return count;}public void backTracking(int[] nums, int target, int startIndex) {if(startIndex==nums.length){if(sum==target)count++;return;}for (int i = 0; i <= 1; i++) {int add=0;if(i==0){add=nums[startIndex];}else if(i==1){add=nums[startIndex]*-1;}sum+=add;backTracking(nums,target,startIndex+1);sum-=add;}}
}二、动态规划
1.dp[j]:凑满容量为j的背包有dp[j]种方法
2.dp[j]=dp[j]+dp[j-nums[i]];这个递归公式的由来:
例如:dp[j],j 为5,
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]种方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]种方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]种方法 凑成 容量为5的背包
- 那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
3.初始化dp[0]=1;
4.遍历
代码:
public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int i:nums){sum+=i;}//如果target的绝对值是大于sum的 那就没有方案if(Math.abs(target)>sum)return 0;//如果sum%2!=0if((target+sum)%2!=0)return 0;int capacity=(target+sum)/2;//定义dp数组int[] dp=new int[capacity+1];//初始化dp数组dp[0]=1;//遍历dp数组for(int i=0;i<nums.length;i++){for(int j=capacity;j>=nums[i];j--){dp[j]+=dp[j-nums[i]];}}return dp[capacity];}注意:这道题为什么可以使用动态规划来做。left为加法的总和,right为减法的总和
left+right=sum; left-right=target; 得出:left=(target+sum)/2;
就是在求有多少种方法可以组成容量为left的
七、一和零(装满容量为i,j有多少种方式)
动态规划:
1.dp[m][n]:求装m个0和n个1有多少种方式
2.dp[m][n]=Math.max(dp[m][n],dp[m-zeroNum][n-oneNum]+1);
3.初始化为0
4.遍历顺序:从后往前遍历,确保每一个元素都只使用一次
代码:
class Solution {public int findMaxForm(String[] strs, int m, int n) {//定义dp数组int[][] dp=new int[m+1][n+1];//dp[i][j],i个0和j个1,装满它们的最大子集是for(String str:strs){int zeroNum,oneNum;for(char ch:str){if(ch=='0')zeroNum++;else oneNum++;}for(int i=m;i>=zeroNum;i--){for(int j=n;j>=oneNum;j--){dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);}}}//返回结果return dp[m][n];}
}0/1背包总结:
1.纯01背包问题:装满x容量的背包最大价值为多少
2.分割等和子集:判断容量为x的背包最大价值是否为x,返回boolean类型
和普通01背包问题一样,就是返回的时候要判断最大价值是否是容量值
3.最后一块石头的重量:容量为x的背包最大价值为多少,
4.目标和:容量为x的背包有多少种方式组成,多少种组合能够装满背包
5.一和零:装满容量为x的背包最多有多少个商品
完全背包理论基础
完全背包:每个商品可以使用无数次
一、零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
分析:多重背包/求使用硬币最少次数
从题目中我们可以看出来,这是一道多重背包的问题,并且是求硬币的最少次数。直接将递推公式写出来:dp[j]=Math.min(dp[j],dp[j-coins[i]]+1);
难点:初始化比较难,因为每次比较都是求使用硬币的最少次数。所以初始化的时候,dp[0]=0之外,其他元素都要初始化成:amount+1。就算全是一元硬币,最多也需要amount次。所以amount+1是不可能实现的一个次数。(我初始化用的Integer.MAX_VALUE,会导致整数溢出)
1.dp[j]:表示凑齐价值为j需要硬币的最小个数
2.dp[j]=Math.min(dp[j],dp[j-coins[i]]+1);
3.初始化:dp[0]=0 Arrays.fill(dp,amount+1);
4.遍历顺序(每个硬币可以使用无数次,因此从coins[i]开始遍历)
5.打印数组xxx
代码:
class Solution {public int coinChange(int[] coins, int amount) {// 动态规划问题 每一个硬币都可以使用无限次// 多重背包问题 凑成价值为amount的最少货币数int[] dp = new int[amount + 1];Arrays.fill(dp, amount+1);//dp[0] = 0;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);}}return dp[amount] > amount ? -1 : dp[amount];}
}二、零钱兑换II(装满背包容量为j的背包有多少种方法)不强调排列 组合数
1.dp[j]:装满j的背包有多少种方法
2.dp[j]+=dp[j-coins[i]];
3.dp[0]=1;(递推公式都基于dp[0] 如果dp[0]=0,那么其他的dp就都等于0)
4.遍历顺序
5.
代码:
class Solution {public int change(int amount, int[] coins) {//多重背包问题 求凑成总价值为amount的货币的种类//求种类的话 状态转移方程就要变化int[] dp=new int[amount+1];dp[0]=1;for(int i=0;i<coins.length;i++){for(int j=coins[i];j<=amount;j++){dp[j]+=dp[j-coins[i]];}}return dp[amount];}
}三、组合总和IV (排列数)
先容量,再商品
public int combinationSum4(int[] nums, int target) {//多重背包 求有多少种方法可以构成targetint[] dp=new int[target+1];dp[0]=1;for(int j=0;j<=target;j++){for(int i=0;i<nums.length;i++){if(j>=nums[i])dp[j]+=dp[j-nums[i]];}}return dp[target];}组合数和排列数问题:
外层商品,内层容量:组合数,不考虑前后顺序。(因为外层商品是按照先后顺序进行的)
外层容量,内层商品:排列数,考虑顺序。

四、完全平方数(类似零钱兑换)
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
相当于:target就是总价格,每一个平方和就是一张纸币。要求完全平方数的最少数量。就是求最少纸币。
1.dp[j]:和为j的完全平方数的最少数量
2.dp[j]=Math.min(dp[j],dp[j-i*i]+1);遇到这个数字,是否选择这个数,如果选择数字就减去,不选择仍然是dp[j]
3.初始化,仍然初始为一个不可能的数字,target+1(就算都为1,也是target张)。dp[0]=0;
4.遍历顺序:先物品再背包
代码:
class Solution {public int numSquares(int n) {// 定义dp[j]:和为j的完全平方数的最少数量int[] dp = new int[n + 1];// 初始化// 其他下标的最大值为n+1(如果都为1的话)Arrays.fill(dp, n);dp[0] = 0;// 先遍历物品 再遍历背包for (int i = 1; i <= (int) Math.sqrt(n); i++) {for (int j = i * i; j <= n; j++) {dp[j] = Math.min(dp[j - i * i] + 1, dp[j]);}}return dp[n];}
}五、单词拆分(排列数 需要考虑顺序)
动态规划:
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
字符串s;字符串列表字典wordDict
1.dp[i](boolean):长度为i的字符串是否由字符串列表组成的
2.if(i>=word.length()&&dp[i-word.length()]==true&&word.equals(s.substring(i-word.length(),i)))
dp[i]=true;
3.dp[0]=true;
思路:在字符串的范围不断往右移动的时候,和字符串字典里面的字符子集进行比较,如果满足条件那么就将dp[i]=true,条件为:.if(i>=word.length()&&dp[i-word.length()]==true&&word.equals(s.substring(i-word.length(),i)))
代码:
public boolean wordBreak(String s, List<String> wordDict) {//对dp数组初始化boolean[] dp=new boolean[s.length()+1];dp[0]=true;//遍历dp数组 排列数 先考虑容量再考虑物品for(int i=0;i<=s.length();i++){for(String word:wordDict){int len=word.length();//字符串的长度if(i>=len&&dp[i-len]==true&&s.substring(i-len,i).equals(word)){dp[i]=true;break;}}}return dp[s.length()];}六、打家劫舍
一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响小偷偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组 nums ,请计算 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
1.dp[i]:从0->i天,小偷偷取商品的最大价值
2.dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i]); 今天偷不偷,今天偷就是dp[i-2]+nums[i];不偷就是dp[i-1];
3.初始化:dp[0]=nums[0];dp[1]=Math.max(nums[0],nums[1]);记住dp[]的含义
4.遍历顺序:从i=2开始
代码:
class Solution {public int rob(int[] nums) {int[] dp=new int[nums.length];//dp[i]的含义是从0-i可以偷的最大值Arrays.fill(dp,0);dp[0]=nums[0];//if(nums.length>1){dp[1]=Math.max(nums[0],nums[1]);}for(int i=2;i<nums.length;i++){dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i]);}printfDp(dp);return dp[nums.length-1];}public void printfDp(int[] dp){for(int i:dp){System.out.print(i+" ");}}
}七、打家劫舍II
在上一道题的基础上,屋子在一个环形的圆圈上排列,首尾也是相邻的
思路:如何破除环?
将带环的情况分成两种线性的情况:
1.将最后一个元素去除掉,然后求长度为size-1的线性表的最大价值
2.将第一个元素去除掉,xxx
也就是求两次dp,然后找一个最大值就行。
代码:
class Solution {public int rob(int[] nums) {int size=nums.length;if(size==1)return nums[0];if(size==2)return Math.max(nums[0],nums[1]);int a1=robAction(nums,0,size-1);int a2=robAction(nums,1,size);return Math.max(a1,a2);}public int robAction(int[] nums, int start, int end) {int size=end-start;int[] dp=new int[size];dp[0]=nums[start];if(size>1){dp[1]=Math.max(nums[start],nums[start+1]);}for(int i=2;i<size;i++){dp[i]=Math.max(dp[i-1],dp[i-2]+nums[start+i]);}return dp[size-1];}
}注意的点:
1.robAction函数中的参数start,end。end是不包括最后一个元素的,实际上的元素是start->end-1;因此在主函数中传入的end函数应该为size/size-1。start的参数没有需要注意的
2.在robAction函数中,dp函数的大小是:end-start。初始化的时候,dp[0]和dp[1];
3.对dp函数遍历的时候,一定要分清楚变量。
for(int i=2;i<size;i++){
dp[i]=Math.max(dp[i-1],dp[i-2]+nums[start+i]);
}
相关文章:

算法学习day12(动态规划)
一、不同的二叉搜索树 二叉搜索树的性质:父节点比左边的孩子节点都大;比右边的孩子节点都小; 由图片可知,dp[3]是可以由dp[2]和dp[1]得出来的。(二叉搜索树的种类和根节点的val有关) 当val为1时,左边是一定没有节点的…...
来动态绑定图片的 src 属性)
Vue 3 <script setup> 使用v-bind(或简写为 :)来动态绑定图片的 src 属性
<img :src"images[currentIndex]" > <template> <div> <!-- 使用 v-bind 或简写为 : 来动态绑定图片的 src 属性 --> <img :src"images[currentIndex]" alt"Dynamic Image" style"width: 100px; height: a…...

前端Vue自定义签到获取积分弹框组件设计与实现
摘要 随着前端技术的不断演进,开发的复杂性日益凸显。传统的整体式开发方式在面临功能迭代和修改时,常常牵一发而动全身,导致开发效率低下和维护成本高昂。组件化开发作为一种解决方案,通过实现模块的独立开发和维护,…...

闲置服务器废物利用_离线下载_私人影院_个人博客_私人云笔记_文件服务器
背景 家里有台旧windows笔记本,PentiumB940 2.00GHz的cpu 4G内存,512G硬盘 放在家里吃灰很久,最近几个月折腾折腾,装了linux操作系统,换了一个2T的硬盘 这里记录下折腾的过程,有需要的可以参考 开通公网IP 打电话给运营商一般都可…...

【Python学习笔记】调参工具Optuna + 泰坦尼克号案例
【Python学习笔记】调参工具Optuna&泰坦尼克号案例 背景前摇:(省流可不看) 最近找了份AI标注师的实习,但是全程都在做文本相关的活,本质上还是拧螺丝,就想着学点调参、部署什么的技能增加一些竞争力&a…...

GPT带我学-设计模式13-策略模式
概述 策略模式 例子 你可以创建一个策略工厂(Strategy Factory)来根据传入的 orgId 动态地选择合适的策略。以下是实现示例: 首先,定义策略接口和具体策略类: public interface CardPathStrategy {String generat…...

【Linux】Ubuntu配置JDK环境、MySQL环境
一、 Ubuntu配置JDK环境 在Ubuntu系统中安装JDK 8可以通过以下步骤进行: 打开终端。更新包列表: sudo apt update安装OpenJDK 8: sudo apt install openjdk-8-jdk验证安装是否成功: java -version注:如果系统中安…...

【ElasticSearch】ES 5.6.15 向量插件支持
参考 : https://github.com/lior-k/fast-elasticsearch-vector-scoring 下载插件 安装插件 插件目录: elasticsearch/plugins, 安装后的目录如下 plugins└── vector├── elasticsearch-binary-vector-scoring-5.6.9.jar└── plugin-descriptor.properties修…...
Kafka 高并发设计之数据压缩与批量消息处理
《Kafka 高性能架构设计 7 大秘诀》专栏第 6 章。 压缩,是一种用时间换空间的 trade-off 思想,用 CPU 的时间去换磁盘或者网络 I/O 传输量,用较小的 CPU 开销来换取更具性价比的磁盘占用和更少的网络 I/O 传输。 Kafka 是一个高吞吐量、可扩展…...
)
设计模式使用场景实现示例及优缺点(行为型模式——模板方法模式)
模板方法模式(Template Method Pattern) 模板方法模式(Template Method Pattern)是一种行为设计模式,它定义了一个操作中的算法的骨架,将算法的一些步骤延迟到子类中。这样可以在不改变算法的结构的前提下…...
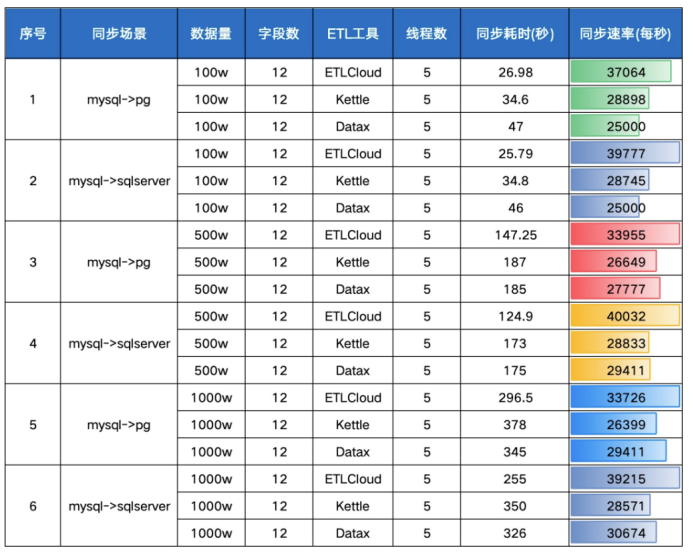
ETL数据集成丨主流ETL工具(ETLCloud、DataX、Kettle)数据传输性能大PK
目前市面上的ETL工具众多,为了方便广大企业用户在选择ETL工具时有一个更直观性能方面的参考值,我们选取了目前市面上最流行的三款ETL工具(ETLCloud、DataX、Kettle)来作为本次性能传输的代表,虽然性能测试数据有很多相…...

eNSP:防火墙设置模拟公司配置(二)
实验拓扑: 实验要求(二): 7: 办公设备可以通过电信连接和移动上网(多对多NAT,并且需要保留一个公网IP) 8: 分公司通过公网移动电信,访问DMZ的http服务器 9&a…...

vue3 两个组件之间传值
Props 父组件可以通过 props 将数据传递给子组件。这是最常见的组件间通信方式 <!-- 父组件 --><template><ChildComponent :message"parentMessage" /></template><script>import ChildComponent from ./ChildComponent.vue;export…...

基于matlab的深度学习案例及基础知识专栏前言
专栏简介 内容涵盖深度学习基础知识、深度学习典型案例、深度学习工程文件、信号处理等相关内容,博客由基于matlab的深度学习案例、matlab基础知识、matlab图像基础知识和matlab信号处理基础知识四部分组成。 一、 基于matlab的深度学习案例 1.1、matlab:基于模…...

机器学习——L1 L2 范数 —>L1 L2正则化
1、L1范数和L2范数是机器学习和数据分析中经常使用的两种范数,它们之间存在多个方面的区别。 以下是关于L1范数和L2范数区别的详细解释: 一、定义差异 L1范数:也被称为曼哈顿范数,是向量元素的绝对值之和。对于一个n维向量x&am…...

大模型时代,还需要跨端framework吗?
跨端 在我近十年的大前端从业经验中,有一半是在和flutter/rn打交道。虽然,flutter和rn官方和社区已经在非常努力的优化、填坑了,但是这两者的坑还是远远高于原生开发。 但是,在锁表的大周期下,华为带着鸿蒙来了&#…...

ASP.NET Core----基础学习05----将数据传递给视图文件的五种情况
文章目录 1. 类型一:使用ViewData将数据传递给视图文件(默认视图文件)2. 类型二:自定义选择视图文件 并传递ViewData数据3. 类型三:使用ViewBag将数据传递给视图文件4. 类型四:在视图文件中使用model转化为…...
Flutter实现局部刷新的几种方式
目录 前言 1.局部刷新的重要性 1.概念 2.重要性 2.局部刷新实现的几种方式 1.使用setState方法进行局部刷新 2.使用StatefulWidget和InheritedWidget局部刷新UI 3.ValueNotifier和ValueListenableBuilder 4.StreamBuilder 5.Provider 6.GetX 7.使用GlobalKey 前言 …...
)
力扣题解(回文子串)
647. 回文子串 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 思路: 首先,本题要求的是数目,而且不要求没…...

对数的基本概念
概念 在数学中,对数是对求幂的逆运算,正如除法是乘法的倒数,反之亦然。这意味着一个数字的对数是必须产生过另一个固定数字(基数)的指数 如果a的x次方等于N(a > 0, 且a不等于1),那么数x叫做以a为底N的…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...

7种分类数据编码技术详解:从原理到实战
在数据分析和机器学习领域,分类数据(Categorical Data)的处理是一个基础但至关重要的环节。分类数据指的是由有限数量的离散值组成的数据类型,如性别(男/女)、颜色(红/绿/蓝)或产品类…...

信息系统分析与设计复习
2024试卷 单选题(20) 1、在一个聊天系统(类似ChatGPT)中,属于控制类的是()。 A. 话语者类 B.聊天文字输入界面类 C. 聊天主题辨别类 D. 聊天历史类 解析 B-C-E备选架构中分析类分为边界类、控制类和实体类。 边界…...
