AC修炼计划(AtCoder Regular Contest 180) A~C
A - ABA and BAB
A - ABA and BAB (atcoder.jp)


这道题我一开始想复杂了,一直在想怎么dp,没注意到其实是个很简单的规律题。
我们可以发现我们住需要统计一下类似ABABA这样不同字母相互交替的所有子段的长度,而每个字段的的情况有(长度+1)/2种,最后所有字段情况的乘积就是最终答案。
#pragma GCC optimize(3) //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
// const int mod=1e9+7;
const int MX=0x3f3f3f3f3f3f3f3f;
//inline int read() //快读
//{
// int xr=0,F=1; char cr;
// while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
// while(cr>='0'&&cr<='9')
// xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
// return xr*F;
//}
//void write(int x) //快写
//{
// if(x<0) putchar('-'),x=-x;
// if(x>9) write(x/10); putchar(x%10+'0');
//}
// 比 unordered_map 更快的哈希表
// #include <ext/pb_ds/assoc_container.hpp>
// using namespace __gnu_pbds;
// const int RANDOM = chrono::high_resolution_clock::now().time_since_epoch().count();
// struct chash {
// int operator()(int x) const { return x ^ RANDOM; }
// };
// typedef gp_hash_table<int, int, chash> hash_t;
constexpr ll mod = 1e9 + 7; //此处为自动取模的数
class modint{ll num;
public:modint(ll num = 0) :num(num % mod){}ll val() const {return num;}modint pow(ll other) {modint res(1), temp = *this;while(other) {if(other & 1) res = res * temp;temp = temp * temp;other >>= 1;}return res;}constexpr ll norm(ll num) const {if (num < 0) num += mod;if (num >= mod) num -= mod;return num;}modint inv(){ return pow(mod - 2); }modint operator+(modint other){ return modint(num + other.num); }modint operator-(){ return { -num }; }modint operator-(modint other){ return modint(-other + *this); }modint operator*(modint other){ return modint(num * other.num); }modint operator/(modint other){ return *this * other.inv(); }modint &operator*=(modint other) { num = num * other.num % mod; return *this; }modint &operator+=(modint other) { num = norm(num + other.num); return *this; }modint &operator-=(modint other) { num = norm(num - other.num); return *this; }modint &operator/=(modint other) { return *this *= other.inv(); }friend istream& operator>>(istream& is, modint& other){ is >> other.num; other.num %= mod; return is; }friend ostream& operator<<(ostream& os, modint other){ other.num = (other.num + mod) % mod; return os << other.num; }
};int n;
string s;
void icealsoheat(){cin>>n;cin>>s;s=" "+s;int res=1;modint ans=1;for(int i=2;i<=n;i++){if(s[i]!=s[i-1]){res++;}else{if(res>=3){ans*=(res+1)/2;}res=1;}}if(res>=3){ans*=(res+1)/2;}cout<<ans;
}
signed main(){ios::sync_with_stdio(false); //int128不能用快读!!!!!!cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}
//
//⠀⠀⠀ ⠀⢸⣿⣿⣿⠀⣼⣿⣿⣦⡀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀ ⠀⢸⣿⣿⡟⢰⣿⣿⣿⠟⠁
//⠀⠀⠀⠀⠀⠀⠀⢰⣿⠿⢿⣦⣀⠀⠘⠛⠛⠃⠸⠿⠟⣫⣴⣶⣾⡆
//⠀⠀⠀⠀⠀⠀⠀⠸⣿⡀⠀⠉⢿⣦⡀⠀⠀⠀⠀⠀⠀ ⠛⠿⠿⣿⠃
//⠀⠀⠀⠀⠀⠀⠀⠀⠙⢿⣦⠀⠀⠹⣿⣶⡾⠛⠛⢷⣦⣄⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣧⠀⠀⠈⠉⣀⡀⠀ ⠀⠙⢿⡇
//⠀⠀⠀⠀⠀⠀⢀⣠⣴⡿⠟⠋⠀⠀⢠⣾⠟⠃⠀⠀⠀⢸⣿⡆
//⠀⠀⠀⢀⣠⣶⡿⠛⠉⠀⠀⠀⠀⠀⣾⡇⠀⠀⠀⠀⠀⢸⣿⠇
//⢀⣠⣾⠿⠛⠁⠀⠀⠀⠀⠀⠀⠀⢀⣼⣧⣀⠀⠀⠀⢀⣼⠇
//⠈⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⢀⣴⡿⠋⠙⠛⠛⠛⠛⠛⠁
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣾⡿⠋⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⢾⠿⠋⠀
//
B - Improve Inversions
B - Improve Inversions (atcoder.jp)


这题确实不好想,但是get到点儿了就会觉得其实也不难。
我们需要尽可能的把逆序对最大化,从样例三我们可以发现,我们不妨确立左边一个要交换的下标i,然后找下标大于等于i+k,数值从大到小的找小于ai的数字,并依次与i的数字进行交换。为了尽可能减少替换的影响,我们按数值从小到大的次序去找这个下标i,从而参与上述的交换。因为我们是按从小到大的顺序的,所以小的数字参与交换并不会影响后面大的数字该交换的逆序对。
#pragma GCC optimize(3) //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
// const int mod=1e9+7;
const int MX=0x3f3f3f3f3f3f3f3f;
//inline int read() //快读
//{
// int xr=0,F=1; char cr;
// while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
// while(cr>='0'&&cr<='9')
// xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
// return xr*F;
//}
//void write(int x) //快写
//{
// if(x<0) putchar('-'),x=-x;
// if(x>9) write(x/10); putchar(x%10+'0');
//}
// 比 unordered_map 更快的哈希表
// #include <ext/pb_ds/assoc_container.hpp>
// using namespace __gnu_pbds;
// const int RANDOM = chrono::high_resolution_clock::now().time_since_epoch().count();
// struct chash {
// int operator()(int x) const { return x ^ RANDOM; }
// };
// typedef gp_hash_table<int, int, chash> hash_t;
// constexpr ll mod = 1e9 + 7; //此处为自动取模的数
// class modint{
// ll num;
// public:
// modint(ll num = 0) :num(num % mod){}// ll val() const {
// return num;
// }// modint pow(ll other) {
// modint res(1), temp = *this;
// while(other) {
// if(other & 1) res = res * temp;
// temp = temp * temp;
// other >>= 1;
// }
// return res;
// }// constexpr ll norm(ll num) const {
// if (num < 0) num += mod;
// if (num >= mod) num -= mod;
// return num;
// }// modint inv(){ return pow(mod - 2); }
// modint operator+(modint other){ return modint(num + other.num); }
// modint operator-(){ return { -num }; }
// modint operator-(modint other){ return modint(-other + *this); }
// modint operator*(modint other){ return modint(num * other.num); }
// modint operator/(modint other){ return *this * other.inv(); }
// modint &operator*=(modint other) { num = num * other.num % mod; return *this; }
// modint &operator+=(modint other) { num = norm(num + other.num); return *this; }
// modint &operator-=(modint other) { num = norm(num - other.num); return *this; }
// modint &operator/=(modint other) { return *this *= other.inv(); }
// friend istream& operator>>(istream& is, modint& other){ is >> other.num; other.num %= mod; return is; }
// friend ostream& operator<<(ostream& os, modint other){ other.num = (other.num + mod) % mod; return os << other.num; }
// };int n,k;
int a[200005];
int p[200005];
vector<PII>ans;
void icealsoheat(){cin>>n>>k;int bns=0;for(int i=1;i<=n;i++)cin>>a[i],p[a[i]]=i;for(int i=1;i<=n;i++){int id=p[i];int x=i;for(int j=i-1;j>=1;j--){if(p[j]>=id+k){// cout<<p[x]<<":::"<<p[j]<<"\n";ans.push_back({p[x],p[j]});a[id]=j;a[p[j]]=x;swap(p[x],p[j]);x=j;}}}cout<<ans.size()<<"\n";for(auto [i,j]:ans){cout<<i<<" "<<j<<"\n";}// for(int i=1;i<=n;i++){// cout<<a[i]<<" ";// }}
signed main(){ios::sync_with_stdio(false); //int128不能用快读!!!!!!cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}
//
//⠀⠀⠀ ⠀⢸⣿⣿⣿⠀⣼⣿⣿⣦⡀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀ ⠀⢸⣿⣿⡟⢰⣿⣿⣿⠟⠁
//⠀⠀⠀⠀⠀⠀⠀⢰⣿⠿⢿⣦⣀⠀⠘⠛⠛⠃⠸⠿⠟⣫⣴⣶⣾⡆
//⠀⠀⠀⠀⠀⠀⠀⠸⣿⡀⠀⠉⢿⣦⡀⠀⠀⠀⠀⠀⠀ ⠛⠿⠿⣿⠃
//⠀⠀⠀⠀⠀⠀⠀⠀⠙⢿⣦⠀⠀⠹⣿⣶⡾⠛⠛⢷⣦⣄⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣧⠀⠀⠈⠉⣀⡀⠀ ⠀⠙⢿⡇
//⠀⠀⠀⠀⠀⠀⢀⣠⣴⡿⠟⠋⠀⠀⢠⣾⠟⠃⠀⠀⠀⢸⣿⡆
//⠀⠀⠀⢀⣠⣶⡿⠛⠉⠀⠀⠀⠀⠀⣾⡇⠀⠀⠀⠀⠀⢸⣿⠇
//⢀⣠⣾⠿⠛⠁⠀⠀⠀⠀⠀⠀⠀⢀⣼⣧⣀⠀⠀⠀⢀⣼⠇
//⠈⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⢀⣴⡿⠋⠙⠛⠛⠛⠛⠛⠁
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣾⡿⠋⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⢾⠿⠋⠀
//
C - Subsequence and Prefix Sum
C - Subsequence and Prefix Sum (atcoder.jp)


一道非常巧妙的dp题,他的状态转移非常的奇妙。
我们考虑前i位的数字对后面数字的贡献值。可以分成两种情况。
1.第i位数字没有被选中
2.第i位数字被选中
当第i位数字被选中时,每一个位数i它所能合成的状态数字都对后面i+1到n的数字有相应的贡献。而这里面0的情况比较特殊,如果第i位的合成数字是0,其实不会改变下一个选中的数字。
这里面有一种情况比较特殊
例如1 -1 5 5 .........
这里我们会发现,我们选择1和-1后,选择第3个5和第4个5的情况是重复的,所以我们要想办法将它去重。
#pragma GCC optimize(3) //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
// const int mod=1e9+7;
const int MX=0x3f3f3f3f3f3f3f3f;
//inline int read() //快读
//{
// int xr=0,F=1; char cr;
// while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
// while(cr>='0'&&cr<='9')
// xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
// return xr*F;
//}
//void write(int x) //快写
//{
// if(x<0) putchar('-'),x=-x;
// if(x>9) write(x/10); putchar(x%10+'0');
//}
// 比 unordered_map 更快的哈希表
// #include <ext/pb_ds/assoc_container.hpp>
// using namespace __gnu_pbds;
// const int RANDOM = chrono::high_resolution_clock::now().time_since_epoch().count();
// struct chash {
// int operator()(int x) const { return x ^ RANDOM; }
// };
// typedef gp_hash_table<int, int, chash> hash_t;
constexpr ll mod = 1e9 + 7; //此处为自动取模的数
class modint{ll num;
public:modint(ll num = 0) :num(num % mod){}ll val() const {return num;}modint pow(ll other) {modint res(1), temp = *this;while(other) {if(other & 1) res = res * temp;temp = temp * temp;other >>= 1;}return res;}constexpr ll norm(ll num) const {if (num < 0) num += mod;if (num >= mod) num -= mod;return num;}modint inv(){ return pow(mod - 2); }modint operator+(modint other){ return modint(num + other.num); }modint operator-(){ return { -num }; }modint operator-(modint other){ return modint(-other + *this); }modint operator*(modint other){ return modint(num * other.num); }modint operator/(modint other){ return *this * other.inv(); }modint &operator*=(modint other) { num = num * other.num % mod; return *this; }modint &operator+=(modint other) { num = norm(num + other.num); return *this; }modint &operator-=(modint other) { num = norm(num - other.num); return *this; }modint &operator/=(modint other) { return *this *= other.inv(); }friend istream& operator>>(istream& is, modint& other){ is >> other.num; other.num %= mod; return is; }friend ostream& operator<<(ostream& os, modint other){ other.num = (other.num + mod) % mod; return os << other.num; }
};int n,k;
int a[500005];
modint dp[105][5005];
modint sum[5005];
void icealsoheat(){cin>>n;for(int i=0;i<=20;i++)if(i!=10)sum[i]=1;for(int i=1;i<=n;i++)cin>>a[i];modint ans=1;for(int i=0;i<n;i++){dp[i][a[i]+1000]=dp[i][a[i]+1000]+sum[a[i]+10];sum[a[i]+10]=0;for(int j=0;j<=2000;j++){if(j==1000)continue;for(int o=i+1;o<=n;o++){// if(j+a[o]<0)cout<<"+++\n";if(j+a[o]<0)continue;dp[o][j+a[o]]+=dp[i][j];ans+=dp[i][j];}}for(int j=0;j<=20;j++){if(j!=10)sum[j]+=dp[i][1000];}}cout<<dp[2][1]<<"+++\n";cout<<ans;}
signed main(){ios::sync_with_stdio(false); //int128不能用快读!!!!!!cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}
//
//⠀⠀⠀ ⠀⢸⣿⣿⣿⠀⣼⣿⣿⣦⡀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀ ⠀⢸⣿⣿⡟⢰⣿⣿⣿⠟⠁
//⠀⠀⠀⠀⠀⠀⠀⢰⣿⠿⢿⣦⣀⠀⠘⠛⠛⠃⠸⠿⠟⣫⣴⣶⣾⡆
//⠀⠀⠀⠀⠀⠀⠀⠸⣿⡀⠀⠉⢿⣦⡀⠀⠀⠀⠀⠀⠀ ⠛⠿⠿⣿⠃
//⠀⠀⠀⠀⠀⠀⠀⠀⠙⢿⣦⠀⠀⠹⣿⣶⡾⠛⠛⢷⣦⣄⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣧⠀⠀⠈⠉⣀⡀⠀ ⠀⠙⢿⡇
//⠀⠀⠀⠀⠀⠀⢀⣠⣴⡿⠟⠋⠀⠀⢠⣾⠟⠃⠀⠀⠀⢸⣿⡆
//⠀⠀⠀⢀⣠⣶⡿⠛⠉⠀⠀⠀⠀⠀⣾⡇⠀⠀⠀⠀⠀⢸⣿⠇
//⢀⣠⣾⠿⠛⠁⠀⠀⠀⠀⠀⠀⠀⢀⣼⣧⣀⠀⠀⠀⢀⣼⠇
//⠈⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⢀⣴⡿⠋⠙⠛⠛⠛⠛⠛⠁
//⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣾⡿⠋⠀
//⠀⠀⠀⠀⠀⠀⠀⠀⢾⠿⠋⠀
//
相关文章:

AC修炼计划(AtCoder Regular Contest 180) A~C
A - ABA and BAB A - ABA and BAB (atcoder.jp) 这道题我一开始想复杂了,一直在想怎么dp,没注意到其实是个很简单的规律题。 我们可以发现我们住需要统计一下类似ABABA这样不同字母相互交替的所有子段的长度,而每个字段的的情况有ÿ…...

云计算练习题
第一题:每周日晚上11点59分需要将/data目录打包压缩到/mnt目录下并以时间命名 #crontab -e 59 23 * * 7 /bin/tar czvf /mnt/date %F-data.tar.gz /data 59 23 * * 7 /bin/tar czvf /mnt/date %T.tar.gz /data 第二题:查找出系统中/application目录下所有…...
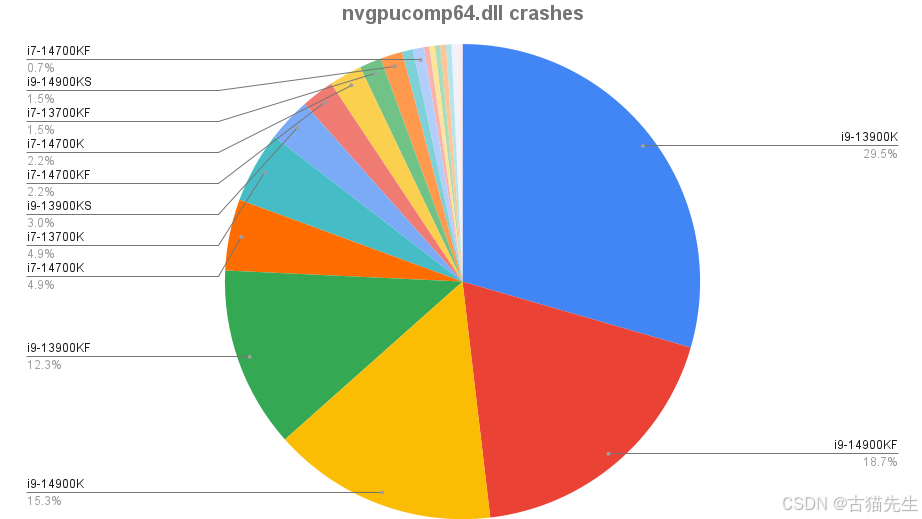
《战甲神兵》开发者报告:游戏崩溃问题80%发生在Intel可超频酷睿i9处理器上——酷睿i7 K系列CPU也表现出高崩溃率
在Intel持续面临第13代和第14代CPU崩溃问题的背景下,近日,《战甲神兵》(Warframe)的开发者们于7月9日披露了游戏崩溃的统计数据,并描述了诊断该问题的过程。根据开发团队的说法,一名未进行超频且使用全新PC的员工,即便…...
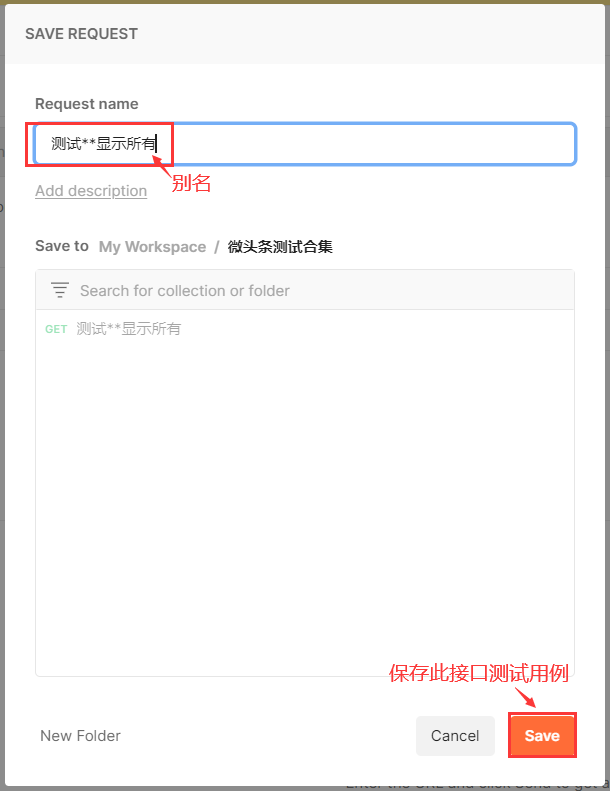
Postman下载及使用说明
Postman使用说明 Postman是什么? Postman是一款接口对接工具【接口测试工具】 接口(前端接口)是什么? 前端发送的请求普遍被称为接口 通常有网页的uri参数格式json/key-value请求方式post/get响应请求的格式json 接…...
什么是im即时通讯?WorkPlus im即时通讯私有化部署安全可控
IM即时通讯是Instant Messaging的缩写,指的是一种实时的、即时的电子信息交流方式,也被称为即时通讯。它通过互联网和移动通信网络,使用户能够及时交换文本消息、语音通话、视频通话、文件共享等信息。而WorkPlus im即时通讯私有化部署则提供…...

hnust 1794: 机器翻译
hnust 1794: 机器翻译 题目描述 小晨的电脑上安装了一个机器翻译软件,他经常用这个软件来翻译英语文章。 这个翻译软件的原理很简单,它只是从头到尾,依次将每个英文单词用对应的中文含义来替换。对于每个英文单词,软件会先在内存…...

AI人工智能开源大模型生态体系分析
人工智能开源大模型生态体系研究 "人工智能开源大模型生态体系研究报告v1.0"揭示,AI(A)的飞速发展依赖于三大核心:数据、算法和算力。这一理念已得到业界广泛认同,三者兼备才能推动AI的壮大发展。随着AI大模型的扩大与普及…...

ArkTS学习笔记_封装复用之@Styles装饰器
ArkTS学习笔记_封装复用之Styles装饰器 背景: 在开发中,如果每个组件的样式都需要单独设置,就会出现大量代码在进行重复样式设置,虽然可以复制粘贴,但为了代码简洁性和后续方便维护,给出的思路是ÿ…...

根据vue学习react
react的函数式组件与vue2是很像的 一、基础类似点 1、组件下拥有一个根节点,vue2是template,react是幽灵标签<> 2、vue2是{{}}以及v-model,react的绑定是{} 3、vue2编译html是v-html,react是{},并且react的jsx中…...
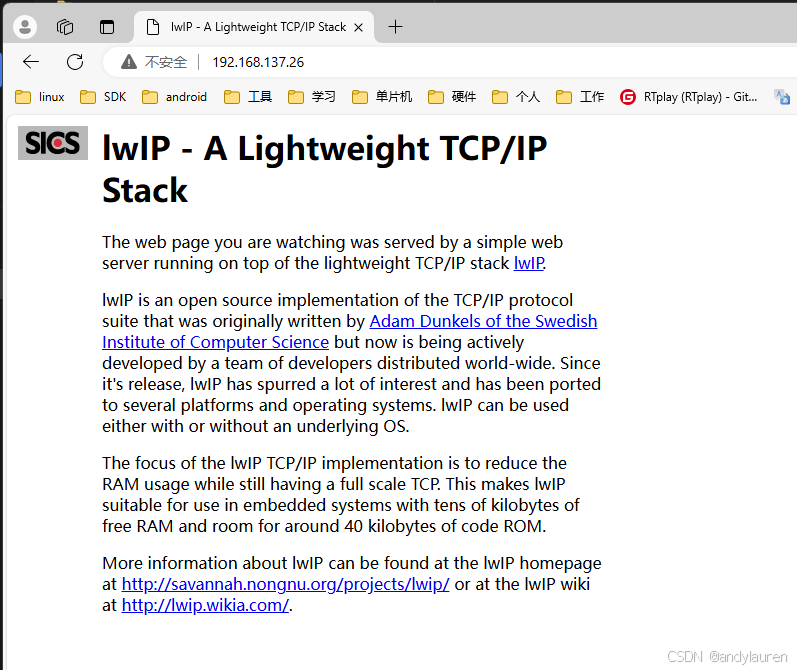
Hi3861 OpenHarmony嵌入式应用入门--HTTPD
httpd 是 Apache HTTP Server 的守护进程名称,Apache HTTP Server 是一种广泛使用的开源网页服务器软件。 本项目是从LwIP中抽取的HTTP服务器代码; Hi3861 SDK中已经包含了一份预编译的lwip,但没有开启HTTP服务器功能(静态库无法…...
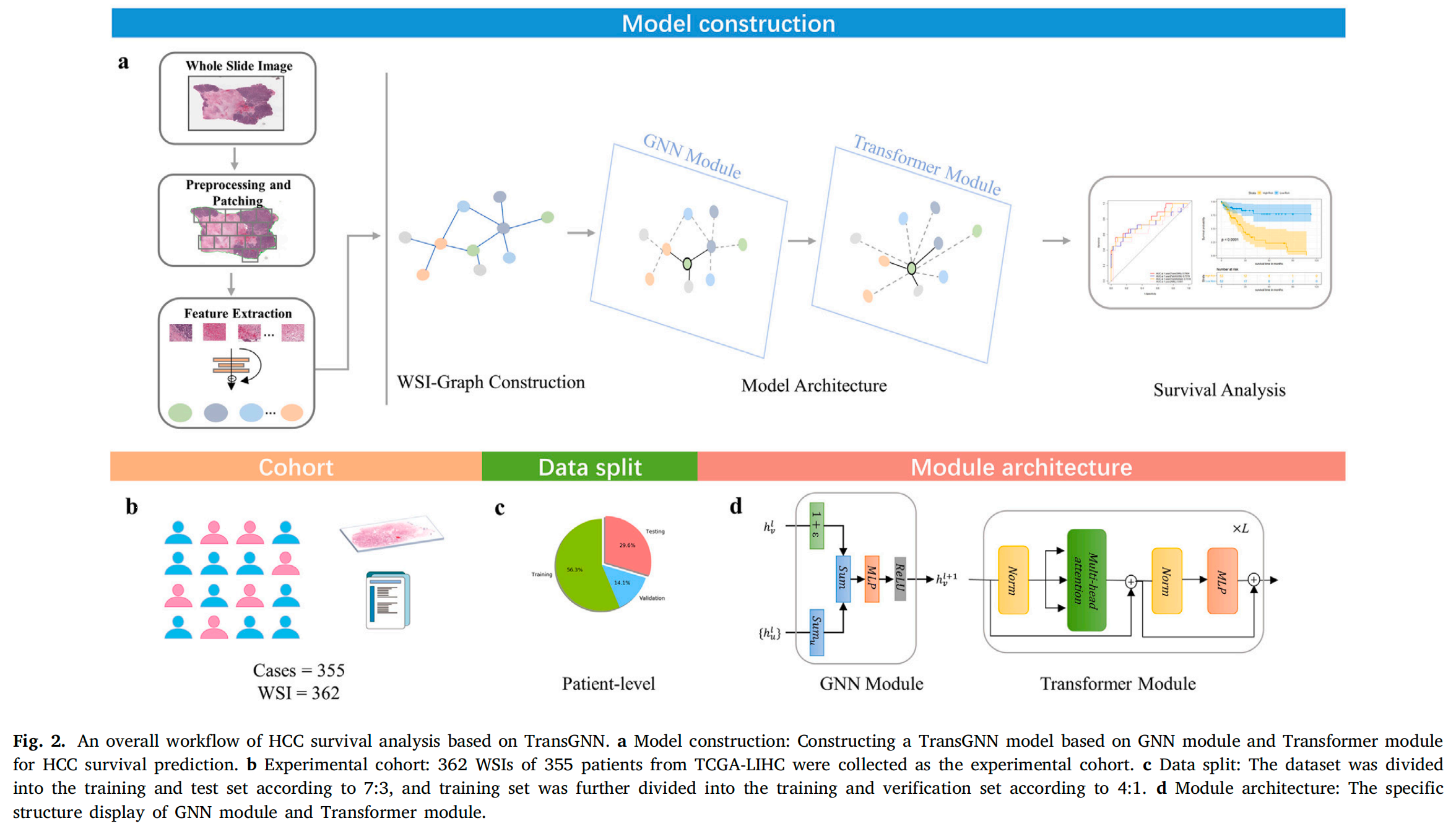
MICS2024|少样本学习、多模态技术以及大语言模型在医学图像处理领域的研究进展|24-07-14
小罗碎碎念 本期推文主题 今天的会议很多主题都集中在大模型、多模态这两个方面,很明显,这两个方向都是目前的研究热点。 所以,我这一期推文会先简单的分析一下秦文健(中科院)和史淼晶(同济大学)…...
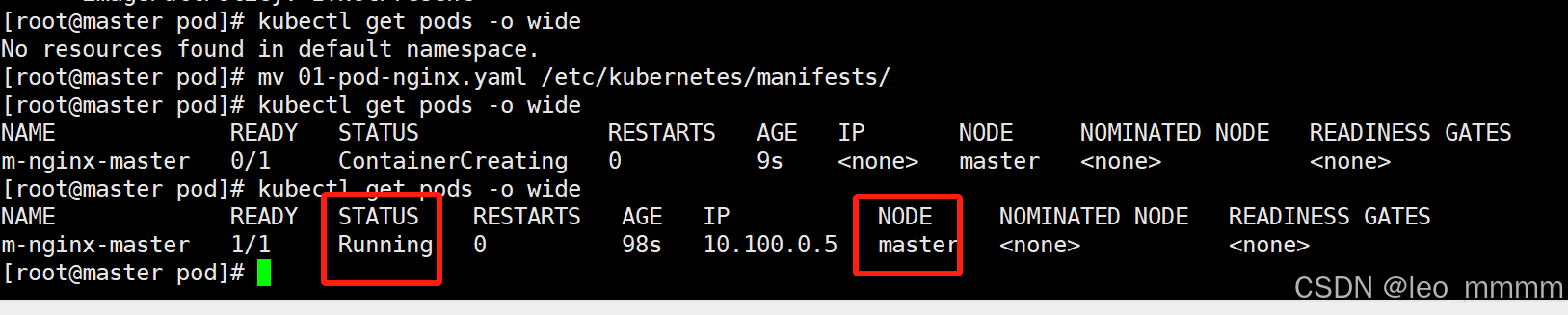
ConfigMap-secrets-静态pod
一.ConfigMap 1.概述 ConfigMap资源,简称CM资源,它生成的键值对数据,存储在ETCD数据库中 应用场景:主要是对应用程序的配置 pod通过env变量引入ConfigMap,或者通过数据卷挂载volume的方式引入ConfigMap资源 官方解释…...

SQL Error: 1406, SQLState: 22001
SQL错误代码1406和SQLState 22001通常表示“列数据过长”错误。这意味着尝试插入或更新列中的值,但该值的长度超过了该列允许的最大长度。 解决此问题的几个步骤: 检查列长度: 确定引起错误的列。检查数据库架构中该列允许的最大长度。 验证…...
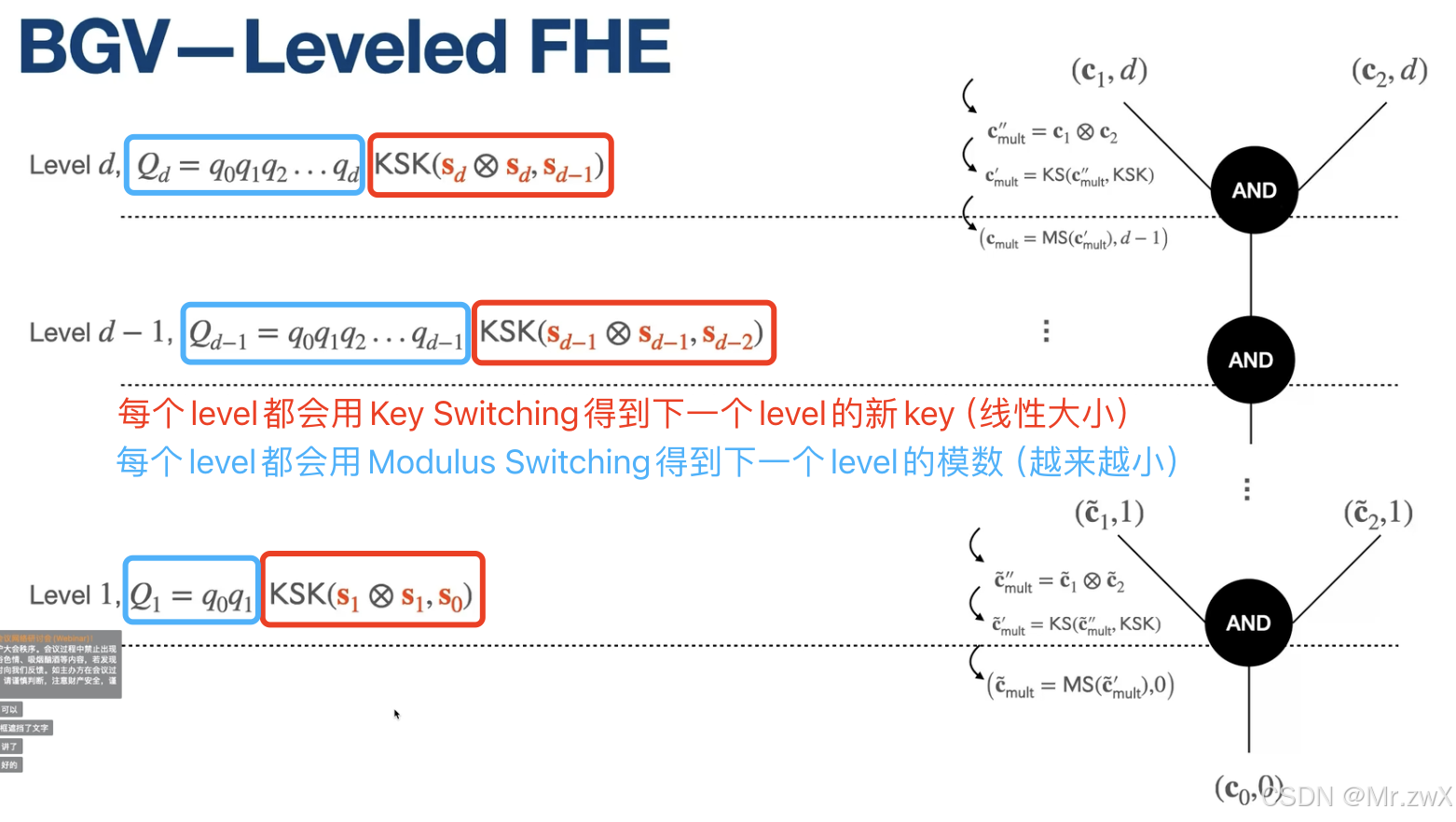
【密码学基础】基于LWE(Learning with Errors)的全同态加密方案
学习资源: 全同态加密I:理论与基础(上海交通大学 郁昱老师) 全同态加密II:全同态加密的理论与构造(Xiang Xie老师) 现在第二代(如BGV和BFV)和第三代全同态加密方案都是基…...
Linux - 基础开发工具(yum、vim、gcc、g++、make/Makefile、git)
目录 Linux软件包管理器 - yum Linux下安装软件的方式 认识yum 查找软件包 安装软件 如何实现本地机器和云服务器之间的文件互传 卸载软件 Linux编辑器 - vim vim的基本概念 vim下各模式的切换 vim命令模式各命令汇总 vim底行模式各命令汇总 vim的简单配置 Linux编译器 - gc…...

网络安全法律框架更新:最新合规要求与企业应对策略
网络安全法律框架的最新更新 近期,中国的网络安全法律框架经历了重要的更新。2022年,《网络安全法》迎来了首次修改,这一修订主要是为了与《数据安全法》和《个人信息保护法》等新实施的法律进行衔接协调,完善法律责任制度&#x…...

数仓工具—Hive语法之正则表达式函数
正则表达式函数 之前我们介绍过like rlike regexp 这些关键字,都是和匹配有关的,今天我们介绍一下hive 的REGEXP_REPLACE 和REGEXP_EXTRACT 函数,背景是使用Hive正则表达式函数提取数字 在我的其他文章中,我们已经看到了如何使用Hive正则表达式从字符串中提取日期值。正则…...

WKCTF 2024 easy_heap
很经典的house of orange unsortedbin attack FSOP 变量覆盖 不能 free,那首先想到就是 house of orange泄露Libc基址,然后unsortedbin attack。 但是只能show(8),就不能用largebin的套路来泄露堆地址了,那怎么办呢? …...

SQL 多变关联使用子查询去重
不去重状态 select a.*,b.recon_amt from free_settlement_first aleft join free_settlement_second b on a.settlement_first_id b.settlement_first_id 有2条数据出现了重复 使用子查询去重 select a.*,b.recon_amt from free_settlement_first aleft join free_settlem…...
)
php表单提交并自动发送邮件给某个邮箱(示例源码下载)
只需要将以下代码内容进行复制即可用到自己的程序/API接口中: <?php if(!empty($_POST[is_post]) && $_POST[is_post]1){$url "https://www.aoksend.com/index/api/send_email";$name $_POST[name];$email $_POST[email];$subject $_POS…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
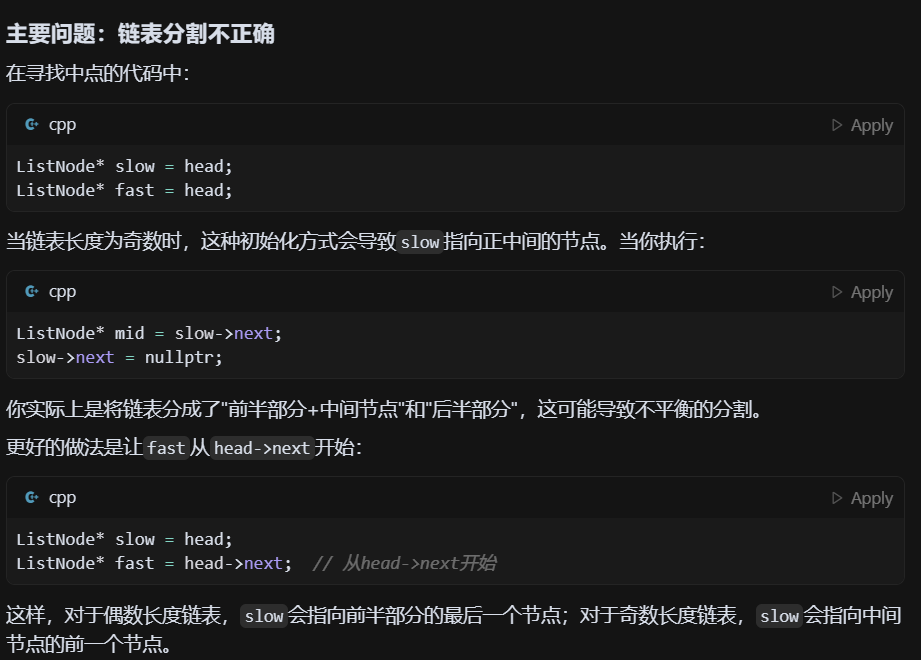
LeetCode - 148. 排序链表
目录 题目 思路 基本情况检查 复杂度分析 执行示例 读者可能出的错误 正确的写法 题目 148. 排序链表 - 力扣(LeetCode) 思路 链表归并排序采用"分治"的策略,主要分为三个步骤: 分割:将链表从中间…...

DriveGPT4: Interpretable End-to-end Autonomous Driving via Large Language Model
一、研究背景与创新点 (一)现有方法的局限性 当前智驾系统面临两大核心挑战:一是长尾问题,即系统在遇到新场景时可能失效,例如突发交通状况或非常规道路环境;二是可解释性问题,传统方法无法解释智驾系统的决策过程,用户难以理解车辆行为的依据。传统语言模型(如 BERT…...

关于疲劳分析的各种方法
疲劳寿命预测方法很多。按疲劳裂纹形成寿命预测的基本假定和控制参数,可分为名义应力法、局部应力一应变法、能量法、场强法等。 1名义应力法 名义应力法是以结构的名义应力为试验和寿命估算的基础,采用雨流法取出一个个相互独立、互不相关的应力循环&…...
