当前位置： 首页 > news >正文

JavaScript(17)——事件监听

news 2026/2/9 1:41:32

什么是事件？

事件是在编程时系统内发生的动作或发生的事情，比如用户在网页上单击一个按钮

什么是事件监听？

就是让程序检测是否有事件产生，一旦有事件触发，就立刻调用一个函数做出响应，也称为绑定事件或注册事件

语法：

元素对象.addEventListener('事件类型',要执行的函数)

事件监听三要素：

  • 事件源： 哪个dom元素被事件触发了，要获取dom元素
  • 事件类型：用什么方式触发，比如鼠标单击click，鼠标经过mouseover等
  • 事件调用的函数：要做什么事

示例：点击按钮弹出对话框

<body><button>点我</button><script>const but = document.querySelector('button')but.addEventListener('click', function () { alert('点我啦') })</script>
</body>

 点击关闭之后，盒子关闭

相关文章：

JavaScript(17)——事件监听

什么是事件&#xff1f; 事件是在编程时系统内发生的动作或发生的事情&#xff0c;比如用户在网页上单击一个按钮 什么是事件监听&#xff1f; 就是让程序检测是否有事件产生&#xff0c;一旦有事件触发&#xff0c;就立刻调用一个函数做出响应&#xff0c;也称为绑定事件或…...

编程日记 2024/7/27 7:25:32

Dav_笔记11：SQL Tuning Overview-sql调优 之 4

开发高效的SQL语句 本节介绍了提高SQL语句效率的方法： ■验证优化程序统计信息 ■审查执行计划 ■重构SQL语句 ■重组索引 ■修改或禁用触发器和约束 ■重组数据 ■随着时间的推移维护执行计划 ■尽可能少地访问数据 验证优化程序统计信息 查询优化器在确定最佳执行…...

编程日记 2024/7/27 7:23:30

vue3引入openlayers

安装ol包 OpenLayers作为 ol npm包提供&#xff0c;它提供了官方支持的API的所有模块。 官方地址&#xff1a;ol npm install ol模块和子模块约定 具有CamelCase名称的OpenLayers模块提供类作为默认导出&#xff0c;并且可能包含其他常量或函数作为命名导出&#xff1a; i…...

编程日记 2024/7/27 7:22:30

大数据管理中心设计规划方案（可编辑的43页PPT）

引言&#xff1a;随着企业业务的快速发展&#xff0c;数据量急剧增长&#xff0c;传统数据管理方式已无法满足高效处理和分析大数据的需求。建立一个集数据存储、处理、分析、可视化于一体的大数据管理中心&#xff0c;提升数据处理能力&#xff0c;加速业务决策过程&#xff0…...

编程日记 2024/7/27 7:21:29

Android --- 广播

广播是什么&#xff1f; 一种相互通信&#xff0c;传递信息的机制&#xff0c;组件内、进程间&#xff08;App之间&#xff09; 如何使用广播&#xff1f; 组成部分 发送者-发送广播 与启动其他四大组件一样&#xff0c;广播发送也是使用intent发送。 设置action&#xff…...

编程日记 2024/7/27 7:17:24

AR 眼镜之-蓝牙电话-实现方案

目录 &#x1f4c2; 前言 AR 眼镜系统版本 蓝牙电话 来电铃声 1. &#x1f531; 技术方案 1.1 结构框图 1.2 方案介绍 1.3 实现方案 步骤一&#xff1a;屏蔽原生蓝牙电话相关功能 步骤二&#xff1a;自定义蓝牙电话实现 2. &#x1f4a0; 屏蔽原生蓝牙电话相关功能 …...

编程日记 2024/7/27 7:15:23

stl-set

目录 目录 内部自动有序、不含重复元素 关于能不能自己造一个cmp&#xff0c;还挺复杂。 访问&#xff1a;只能用迭代器且受限 添加元素&#xff1a;没有pushback&#xff0c;用insert 复杂度&#xff1a;ologn ​编辑 查找元素find&#xff08;&#xff09;&#xff1…...

编程日记 2024/7/27 7:14:22

【Stable Diffusion】（基础篇五）—— 使用SD提升分辨率

使用SD提升分辨率 本系列博客笔记主要参考B站nenly同学的视频教程&#xff0c;传送门&#xff1a;B站第一套系统的AI绘画课&#xff01;零基础学会Stable Diffusion&#xff0c;这绝对是你看过的最容易上手的AI绘画教程 | SD WebUI 保姆级攻略_哔哩哔哩_bilibili 在前期作画的…...

编程日记 2024/7/27 7:13:21

5.CSS学习（浮动）

浮动&#xff08;float&#xff09; 是一种传统的网页布局方式&#xff0c;通过浮动&#xff0c;可以使元素脱离文档流的控制&#xff0c;使其横向排列。 其编写在CSS样式中。 float:none(默认值) 元素不浮动。 float:left 设置的元素在其包含…...

编程日记 2024/7/27 7:12:19

Spring Cloud微服务项目统一封装数据响应体

在微服务架构下&#xff0c;处理服务之间的通信和数据一致性是一个重要的挑战。为了提高开发效率、保证数据的一致性及简化前端开发&#xff0c;统一封装数据响应体是一种非常有效的实践。本文博主将介绍如何在 Spring Cloud 微服务项目中统一封装数据响应体&#xff0c;并分享…...

编程日记 2024/7/27 7:09:16

java算法day20

java算法day20 701.二叉搜索树中的插入操作450.删除二叉搜索树中的节点108 将有序数组转换为二叉搜索树 本次的题目都是用递归函数的返回值来完成&#xff0c;多熟悉这样的用法&#xff0c;很方便。 其实我感觉&#xff0c;涉及构造二叉树的题目&#xff0c;用递归函数的返回值…...

编程日记 2024/7/27 7:05:12

web自动化测试-python+selenium+unitest

文章目录 Web自动化测试工具1. 主流的Web自动化测试工具2. Selenium家族史 Web自动化测试环境搭建基于Python环境搭建示例&#xff1a;通过程序启动浏览器&#xff0c;并打开百度首页&#xff0c;暂停3秒&#xff0c;关闭浏览器 页面元素定位1. 如何进行元素定位&#xff1f;2.…...

编程日记 2024/7/27 7:03:10

LeetCode题练习与总结：组合两个表--175

一、题目描述 SQL Schema > Pandas Schema > 表: Person ---------------------- | 列名 | 类型 | ---------------------- | PersonId | int | | FirstName | varchar | | LastName | varchar | ---------------------- personId 是该表的主…...

编程日记 2024/7/27 7:02:09

数据结构：二叉搜索树（简单C++代码实现）

目录 前言 1. 二叉搜索树的概念 2. 二叉搜索树的实现 2.1 二叉树的结构 2.2 二叉树查找 2.3 二叉树的插入和中序遍历 2.4 二叉树的删除 3. 二叉搜索树的应用 3.1 KV模型实现 3.2 应用 4. 二叉搜索树分析 总结 前言 本文将深入探讨二叉搜索树这一重要的数据结构。二…...

编程日记 2024/7/27 6:58:05

深入理解Prompt工程

前言&#xff1a;因为大模型的流行&#xff0c;衍生出了一个小领域“Prompt工程”&#xff0c;不知道大家会不会跟小编一样&#xff0c;不就是写提示吗&#xff0c;这有什么难的&#xff0c;不过大家还是不要小瞧了Prompt工程&#xff0c;现在很多大模型把会“Prompt工程”作为…...

编程日记 2024/7/27 6:57:03

代码随想录算法训练营day6 | 242.有效的字母异位词、349. 两个数组的交集、202. 快乐数、1.两数之和

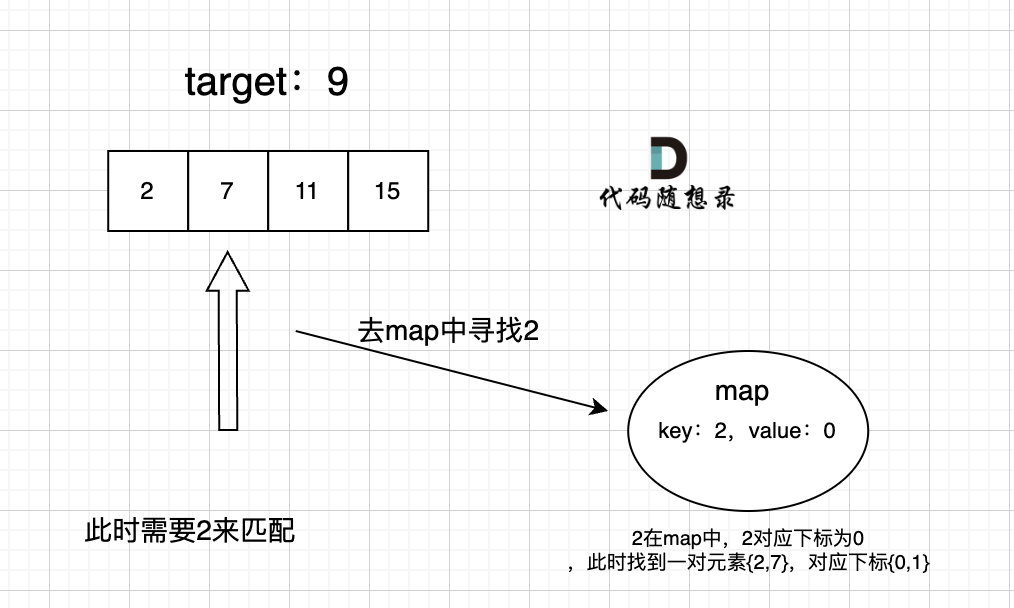
文章目录 哈希表键值 哈希函数哈希冲突拉链法线性探测法 常见的三种哈希结构集合映射C实现std::unordered_setstd::map 小结242.有效的字母异位词思路复习 349. 两个数组的交集使用数组实现哈希表的情况思路使用set实现哈希表的情况 202. 快乐数思路 1.两数之和思路 总结 今天是…...

编程日记 2024/7/27 6:52:58

vue3 vxe-table 点击行，不显示选中状态，加上设置isCurrent: true就可以设置选中行的状态。

1、上个图&#xff0c;要实现这样的&#xff1a; Vxe Table v4.6 官方文档 2、使用 row-config.isCurrent 显示高亮行&#xff0c;当前行是唯一的&#xff1b;用户操作点击选项时会触发事件 current-change <template><div><p><vxe-button click"sel…...

编程日记 2024/7/27 6:50:56

Linux没有telnet 如何测试对端的端口状态

前段时间有人问uos没有telnet&#xff0c;又找不到包。 追问了一下为什么非要安装telnet&#xff0c;答复是要测试对端的端口号。 这里简单介绍一下&#xff0c;测试端口号的方法有很多&#xff0c;telent只是在windows上经常使用&#xff0c;linux已很少安装并使用该命令&…...

编程日记 2024/7/27 6:46:52

花几千上万学习Java，真没必要！（二十九）

1、基本数据类型包装类&#xff1a; 测试代码1&#xff1a; package apitest.com; //使用Integer类的不同方法处理整数。 //将字符串转换为整数&#xff08;parseInt&#xff09;和Integer对象&#xff08;valueOf&#xff09;&#xff0c; //将整数转换回字符串&#xff08;…...

编程日记 2024/7/27 6:45:51

C#如何引用dll动态链接库文件的注释

1、dll动态库文件项目生成属性中要勾选“XML文档文件” 注意&#xff1a;XML文件的名字切勿修改。 2、添加引用时XML文件要与DLL文件在同一个目录下。 3、如果要是添加引用的时候XML不在相同目录下&#xff0c;之后又将XML文件复制到相同的目录下&#xff0c;需要删除引用&am…...

编程日记 2024/7/27 6:44:50

Docker 离线安装指南

参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性&#xff0c;不同版本的Docker对内核版本有不同要求。例如&#xff0c;Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本&#xff0c;Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

编程新知 2026/2/7 6:10:30

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

《通信之道——从微积分到 5G》读书总结

第1章 绪 论 1.1 这是一本什么样的书 通信技术&#xff0c;说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号&#xff08;调制&#xff09; 把信息从信号中抽取出来&am…...

编程新知 2026/2/7 11:01:56

Nuxt.js 中的路由配置详解

Nuxt.js 通过其内置的路由系统简化了应用的路由配置&#xff0c;使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

编程新知 2026/2/6 16:52:42

python如何将word的doc另存为docx

将 DOCX 文件另存为 DOCX 格式&#xff08;Python 实现&#xff09; 在 Python 中&#xff0c;你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是&#xff0c;.doc 是旧的 Word 格式&#xff0c;而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

编程新知 2025/12/13 22:42:30

浅谈不同二分算法的查找情况

二分算法原理比较简单&#xff0c;但是实际的算法模板却有很多&#xff0c;这一切都源于二分查找问题中的复杂情况和二分算法的边界处理&#xff0c;以下是博主对一些二分算法查找的情况分析。 需要说明的是&#xff0c;以下二分算法都是基于有序序列为升序有序的情况&#xf…...

编程新知 2025/9/14 7:37:32

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台

🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...

编程新知 2026/1/25 3:31:07

Python ROS2【机器人中间件框架】 简介

销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

编程新知 2026/1/29 9:12:46

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档&#xff09;&#xff0c;如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下&#xff0c;风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

编程新知 2026/1/25 4:19:49

STM32HAL库USART源代码解析及应用

STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

编程新知 2026/1/31 13:18:46