数据结构之二叉树构建、广度/深度优先(前序、中序、后序)遍历
一、二叉树
1.1 树
说到树,我们暂时忘记学习,来看一下大自然的树:

哈哈 以上照片是自己拍的,大家凑合看看
回归正题,那么在数据结构中,树是什么呢,通过上面的图片大家也可以理解
树是一种非线性的数据结构
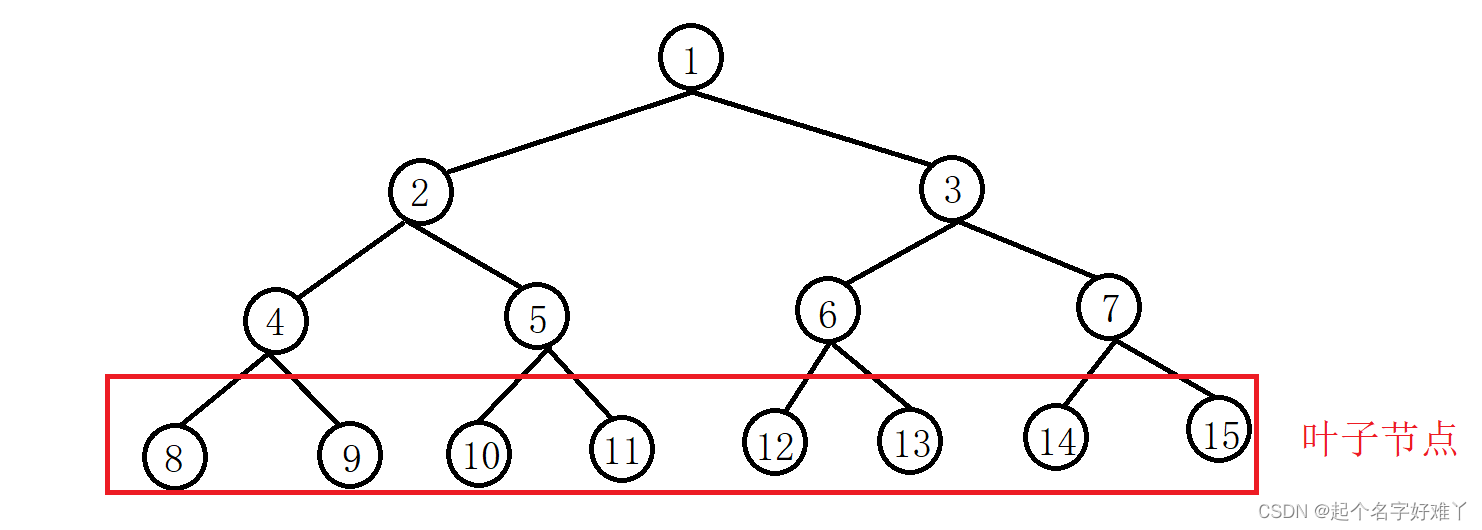
像这样 ,有多个节点组成的有一定层次关系的结构,像是一颗相对于天空逆生长的一颗树,节点像是一片片树叶,黑色的线条像是树枝,而最顶上的那个节点像是树根,因此得名 树
2.2 二叉树
二叉树长什么样子呢?
来看一下大自然的 “二叉树”

百度出来的图
是不是下面这个样子
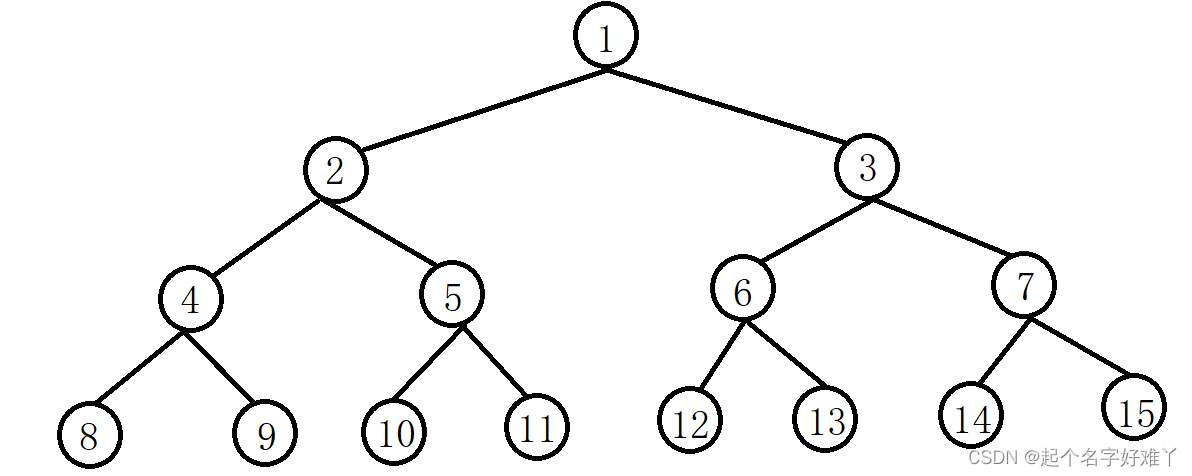
从根开始,开始分叉,每次只分两个叉,就这样一直分下去
二叉树有什么特点呢?
1.最顶上的那个节点叫做整棵树的 根节点
2.根据根节点可以将整棵树划分为 左右子树
3.叶子节点,像最末端的 8~15 ,没有继续分叉的,就是叶子节点了,只要还继续有分叉的不被叫做叶子节点,叶子没法分叉了对吧
4.Parents 双亲节点(父母节点) 像 1 就是 2 、3 的 双亲节点,有时候也叫父节点,或者说,相对于 4 5 来说,2 就像是根节点一样
5. 左孩子、右孩子 ,像 4 就是 2 的左孩子节点、5 是 2 的右孩子节点
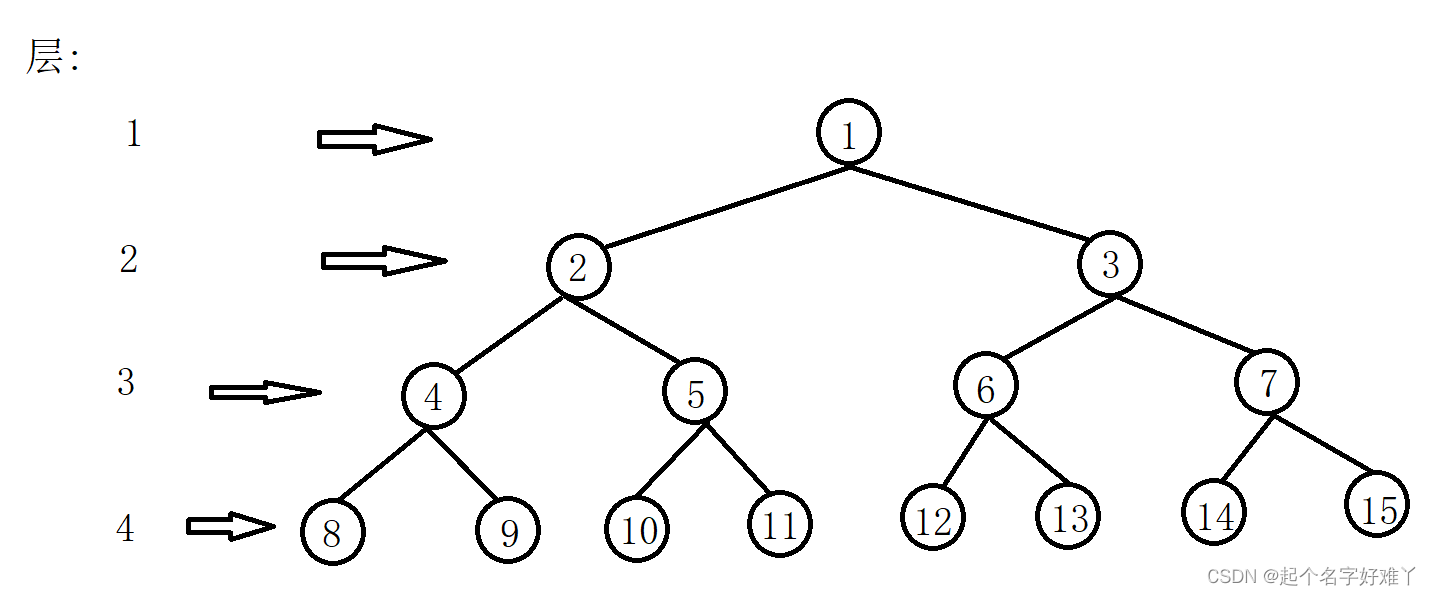
6.层:4 层
7.树的高度:每加一层 代表树的高度 + 1 像上图树的高度就是 4
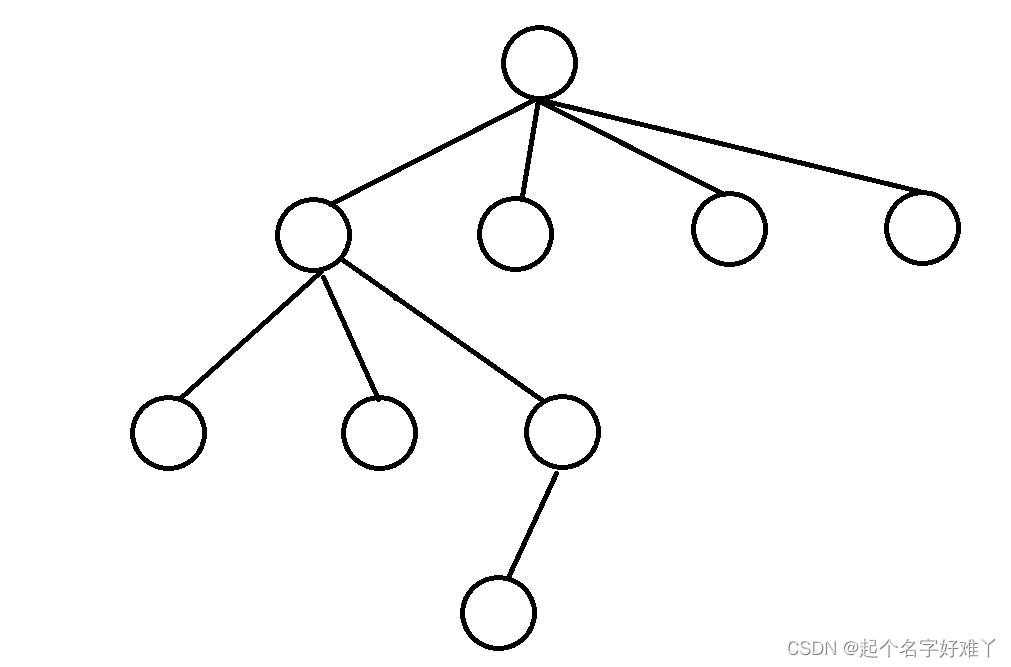
8.节点的度 ,这里的度指的是 “出度” 就是 一个 双亲节点 有几个 孩子节点 像 节点 2 的 度就是 2,而像之前说的 不是二叉树的树,像这样:节点 1 的出度就是 4
大概了解了二叉树的特点之后我们再来看一下下面这两个比较特殊的二叉树
2.2.1 满二叉树
也就是每一层的节点数都达到最大值,满满的没有空缺的,除了最后一层的叶子节点外,所有的节点都拥有两个孩子节点,就是下面这个样子
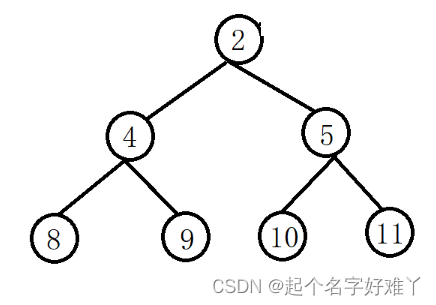
2.2.2 完全二叉树
完全二叉树,就是在满二叉树的基础上,允许每个节点不一定分两个叉,也就是说
满二叉树,除了叶子节点,其他的所有节点的度都是 2
完全二叉树,并不是所有的节点的度都是 2 ,但是 这一特定仅限定于倒数第二层的节点,例如:
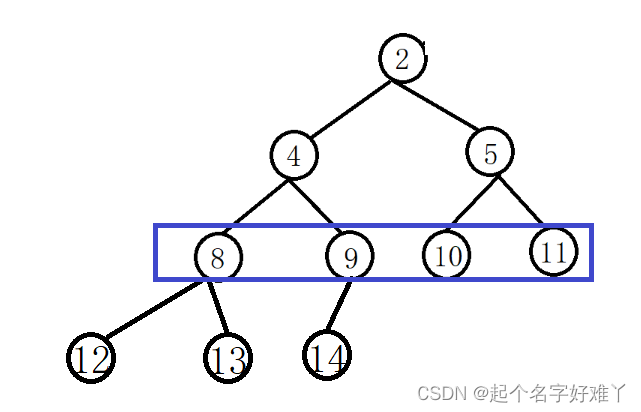
允许 节点 9 的 度 为 1 ,每个节点的子节点(左孩子、右孩子)必须严格按照现有左再有右的顺序,
不允许
1.没有左孩子节点但是有右孩子节点,例如:

2.从上至下,按层往下,除了最后一层,其他层未达到最大节点数,例如:
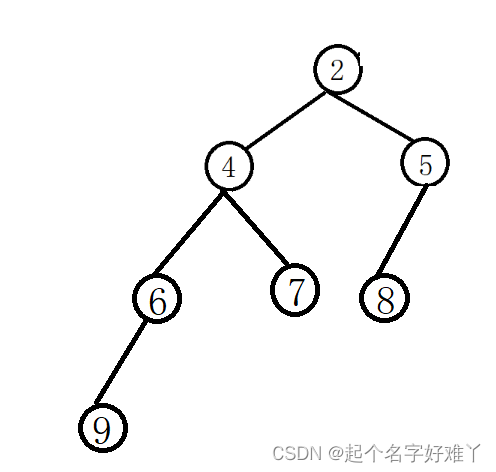
总结:
满二叉树 从上到下,从左至右,从 0 ~ n 中间 不间断
完全二叉树:每一层(根节点为第 0 层)的节点数都满足 2^n 个
二、顺序存储构建二叉树
例如:给定一个vector 包含若干个元素,要求按照元素的顺序构建出一颗二叉树

刚开始可能没有思路,那我们先看一下二叉树的特点
1.需要存储当前节点的值
2.通过该节点可以找到左孩子、右孩子
通过上述两个特点,我们可以想象出二叉树每个节点的大概结构
1.data 存储节点的值
2.left 指针 ,访问该节点的左孩子节点
3.right 指针,访问该节点的右孩子节点
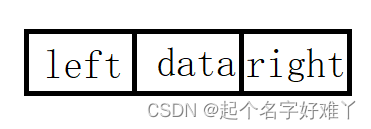
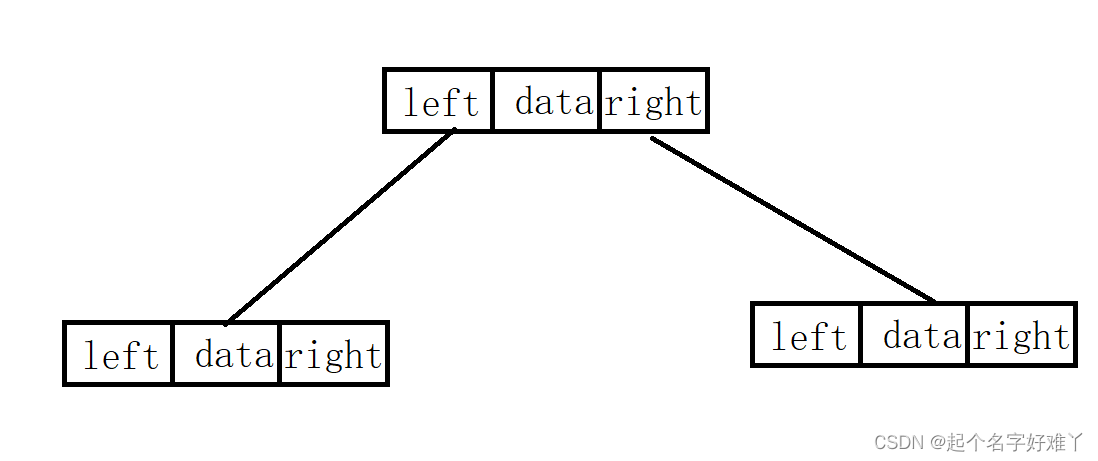
代码则为:
struct TreeNode
{int val;TreeNode* left;TreeNode* right;
};
二叉树的节点类型确定了,那么我们如何将数组中的元素,构建成一个逻辑上的树形结构呢?
我们来分析一下数组元素下标与构建成功之后的二叉树的下标关系

通过分析二叉树中元素下标我们可以总结一下规律:
设 当前节点的元素下标为 n ,那么该节点的左孩子 节点元素下标为 2n + 1,右孩子节点元素下标为 2n+2;
例如:
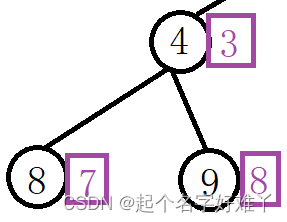
现在将节点和数组元素的关系理清之后,接下来需要考虑如何将数组中的元素逐个,按照二叉树中从上至下,从左至右构建。
这里我们需要用到队列来控制从上至下、从左至右顺序;
通过入队(根、左、右)、取队头、出队,保持顺序,通过元素下标控制节点的值
TreeNode* MakeBinaryTree(vector<int>& vctTemp){if (vctTemp.empty()){cout << "vector is empty" << endl;return nullptr;}else{//先将根节点入队TreeNode* root = new TreeNode();root->val = vctTemp[0];root->left = nullptr;root->right = nullptr;queue<TreeNode*> quTemp;quTemp.push(root);//元素下标int n = 0;while (!quTemp.empty()){ //先取出队头元素TreeNode* nodeTemp = quTemp.front();quTemp.pop();//计算左孩子节点下标int leftIndex = 2 * n + 1;if (leftIndex <= vctTemp.size() - 1){//构建左孩子节点TreeNode* leftnode = new TreeNode();leftnode->val = vctTemp[leftIndex];leftnode->left = nullptr;leftnode->right = nullptr;nodeTemp->left = leftnode;quTemp.push(leftnode);}//计算右孩子节点下标int rightIndex = 2 * n + 2;if (rightIndex <= vctTemp.size() - 1){//构建右孩子节点TreeNode* rightnode = new TreeNode();rightnode->val = vctTemp[rightIndex];rightnode->left = nullptr;rightnode->right = nullptr;nodeTemp->right = rightnode;quTemp.push(rightnode);}//下标 + 1,每次仅出队一个元素n++;}return root;}}
三、常规遍历方法
3.1 广度优先遍历
广度优先遍历 英文简称为:BFS (Breadth-First-Search)

广度优先从上至下,从左至右依次进行遍历,这里是不是想到了我们构建的时候也是按照从上至下,从左至右的构建顺序,没错这种方法就是 BFS 广度优先遍历
按照构建的思路,我们同样需要一个队列来辅助我们进行顺序控制
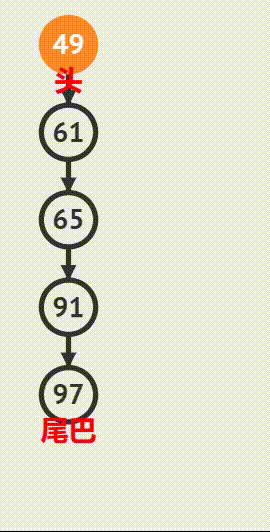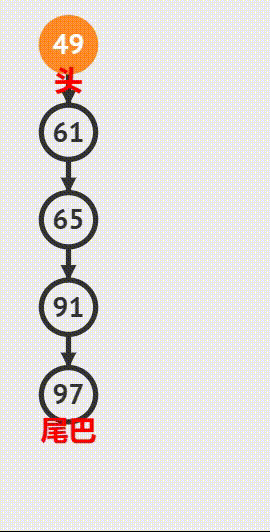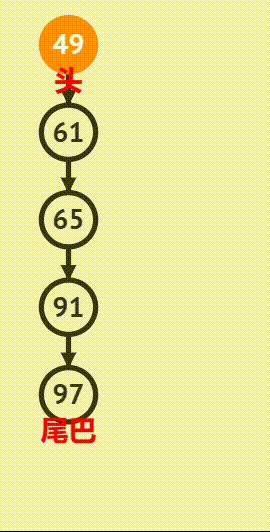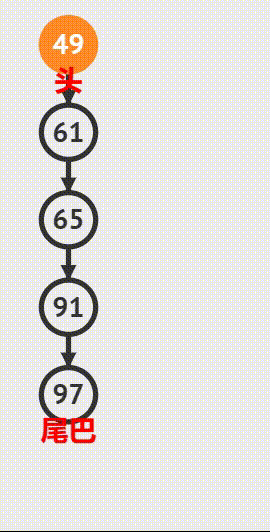
图示:
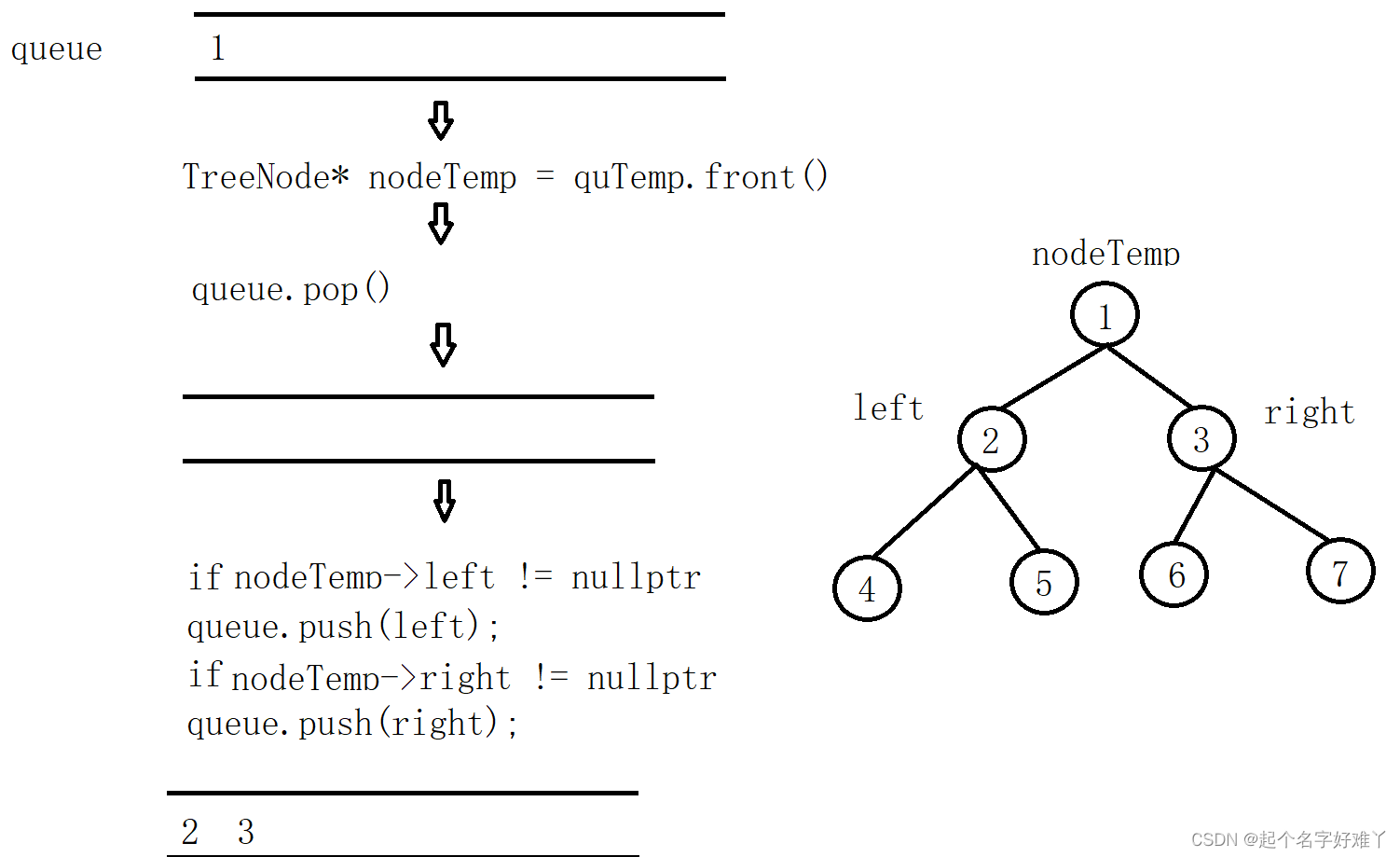

直到最后一个叶子节点 7 pop 出去,queue 为空循环结束,整个二叉树也遍历完成
代码示例:
void BFS(TreeNode* root){if (root == nullptr){cout << " root is empty" << endl;}else{vector<int> vctResult;queue<TreeNode*> quTemp;//先将根节点入队quTemp.push(root);vctResult.push_back(root->val);while (!quTemp.empty()){//取队头TreeNode* nodeTemp = quTemp.front();quTemp.pop();//左孩子不为空,先将左孩子入队if (nodeTemp->left != nullptr){quTemp.push(nodeTemp->left);vctResult.push_back(nodeTemp->left->val);}//右孩子不为空,再将右孩子入队if (nodeTemp->right != nullptr){quTemp.push(nodeTemp->right);vctResult.push_back(nodeTemp->right->val);}}//打印元素Print(vctResult);}}
运行:
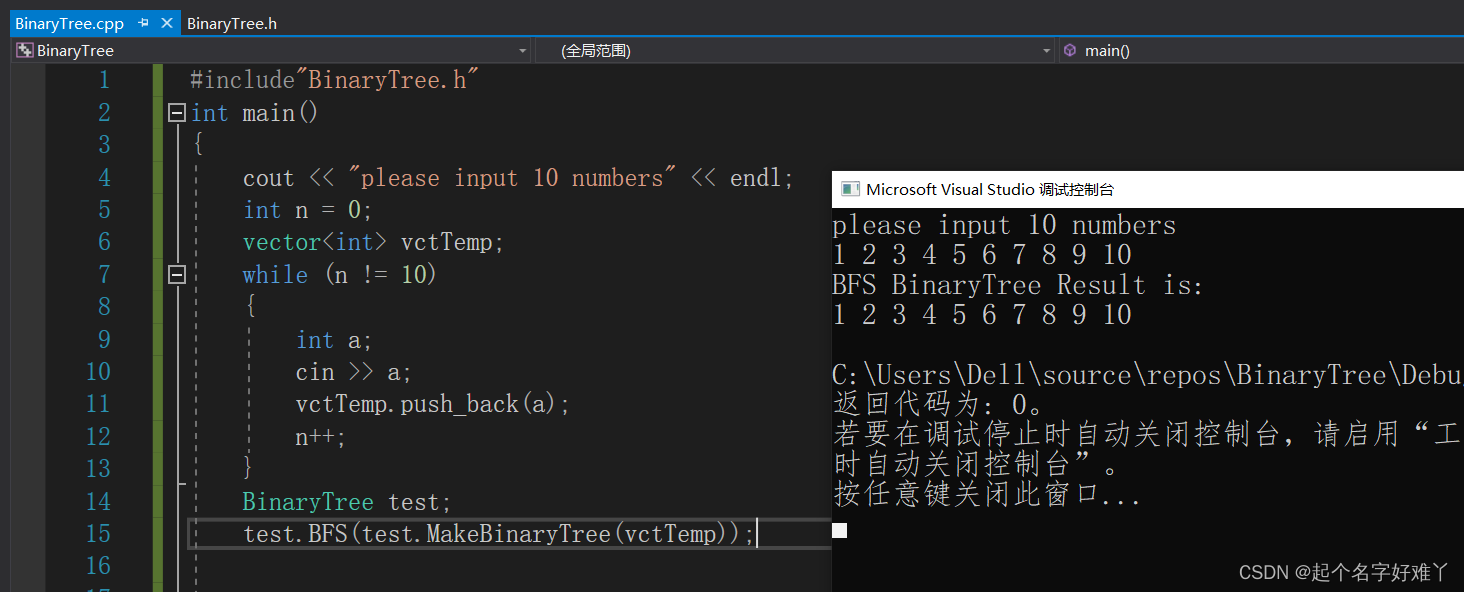
3.2 深度优先遍历
深度优先遍历不同于广度优先那样一层一层、从左至右遍历,而是按照前序或中序、或后序那样,从根节点不断的向下遍历,并将整棵树分左右子树,先将一颗子树遍历完(达到该子树的叶子节点)再去遍历另一棵树,因此被称为深度优先遍历。
深度优先遍历顺序又分为一下三种遍历方法:
以下是我整理的一篇二叉树的 前/中/后序 逻辑图形示例,不清楚逻辑的可以先看一下:
二叉树的前序/中序/后序遍历新手入门介绍
图示:

3.2.1前序遍历
前序遍历:遍历顺序(先根、再左、再右) DLR
递归遍历代码为:
void DLR(TreeNode* root){if (root == nullptr){return;}cout << root->val << " ";DLR(root->left);DLR(root->right);}
关于递归的思想我们这里以前序遍历做详细的步骤分析,帮助大家理解递归的思路和思想

关于递归,大家可以有时候想不到递归函数如何去写,可以考虑以下三个方面,来思考递归怎么写
1.函数调用自身
2.函数终止条件
3.向终止条件前进的执行动作
例如:
//递归函数本身void DLR(TreeNode* root){//终止条件if (root == nullptr){return;}cout << root->val << " ";//不断向叶子节点遍历,逼近 root == nullptr 条件//调用函数自身DLR(root->left);DLR(root->right);}
3.2.2 中序遍历
中序遍历:遍历顺序(先左、再根、再右)
递归遍历代码为:
void LDR(TreeNode* root){if (root == nullptr){return;}LDR(root->left);cout << root->val << " ";LDR(root->right);}
3.2.3后序遍历
后序遍历:遍历顺序(先左、再右、再根)
递归遍历代码为:
//后序遍历void LRD(TreeNode* root){if (root == nullptr){return;}LRD(root->left);LRD(root->right);cout << root->val << " ";}
完整测试代码如下:
BinaryTree.h
#pragma once
#include<iostream>
#include<vector>
#include<queue>
using namespace std;struct TreeNode
{int val;TreeNode* left;TreeNode* right;
};class BinaryTree
{
public:BinaryTree(){}~BinaryTree(){}TreeNode* MakeBinaryTree(vector<int>& vctTemp){if (vctTemp.empty()){cout << "vector is empty" << endl;return nullptr;}else{TreeNode* root = new TreeNode();root->val = vctTemp[0];root->left = nullptr;root->right = nullptr;queue<TreeNode*> quTemp;quTemp.push(root);int n = 0;while (!quTemp.empty()){TreeNode* nodeTemp = quTemp.front();quTemp.pop();int leftIndex = 2 * n + 1;if (leftIndex <= vctTemp.size() - 1){TreeNode* leftnode = new TreeNode();leftnode->val = vctTemp[leftIndex];leftnode->left = nullptr;leftnode->right = nullptr;nodeTemp->left = leftnode;quTemp.push(leftnode);}int rightIndex = 2 * n + 2;if (rightIndex <= vctTemp.size() - 1){TreeNode* rightnode = new TreeNode();rightnode->val = vctTemp[rightIndex];rightnode->left = nullptr;rightnode->right = nullptr;nodeTemp->right = rightnode;quTemp.push(rightnode);}n++;}return root;}}void BFS(TreeNode* root){if (root == nullptr){cout << " root is empty" << endl;}else{vector<int> vctResult;queue<TreeNode*> quTemp;quTemp.push(root);vctResult.push_back(root->val);while (!quTemp.empty()){TreeNode* nodeTemp = quTemp.front();quTemp.pop();if (nodeTemp->left != nullptr){quTemp.push(nodeTemp->left);vctResult.push_back(nodeTemp->left->val);}if (nodeTemp->right != nullptr){quTemp.push(nodeTemp->right);vctResult.push_back(nodeTemp->right->val);}}cout << "BFS BinaryTree Result is:" << endl;Print(vctResult);}}//前序遍历void DLR(TreeNode* root){if (root == nullptr){return;}cout << root->val << " ";DLR(root->left);DLR(root->right);}//中序遍历void LDR(TreeNode* root){if (root == nullptr){return;}LDR(root->left);cout << root->val << " ";LDR(root->right);}//后序遍历void LRD(TreeNode* root){if (root == nullptr){return;}LRD(root->left);LRD(root->right);cout << root->val << " ";}void Print(vector<int> &vctTemp){for (auto a : vctTemp){cout << a << " ";a++;}cout << endl;}
private:vector<int> m_vector;};
BinaryTree.cpp
#include"BinaryTree.h"
int main()
{cout << "please input 10 numbers" << endl;int n = 0;vector<int> vctTemp;while (n != 10){int a;cin >> a;vctTemp.push_back(a);n++;}BinaryTree test;TreeNode* root = test.MakeBinaryTree(vctTemp);test.BFS(root);cout << "前序遍历结果为:" << endl;test.DLR(root);cout << endl;cout << "中序遍历结果为:" << endl;test.LDR(root);cout << endl;cout << "后序遍历结果为:" << endl;test.LRD(root);cout << endl;return 0;
}
相关文章:

数据结构之二叉树构建、广度/深度优先(前序、中序、后序)遍历
一、二叉树 1.1 树 说到树,我们暂时忘记学习,来看一下大自然的树: 哈哈 以上照片是自己拍的,大家凑合看看 回归正题,那么在数据结构中,树是什么呢,通过上面的图片大家也可以理解 树是一种非…...

“国产版ChatGPT”文心一言发布会现场Demo硬核复现
文章目录前言实验结果一、文学创作问题1 :《三体》的作者是哪里人?问题2:可以总结下三体的核心内容吗?如果要续写的话,可以从哪些角度出发?问题3:如何从哲学角度来进行续写?问题4:电…...

202304读书笔记|《不被定义的女孩》——做最真实最漂亮的自己,依心而行
202304读书笔记|《不被定义的女孩》——做最真实最漂亮的自己,依心而行《不被定义的女孩》作者ASEN,很棒的书。处处透露着洒脱,通透,悦己,阅世界的自由的氛围和态度! 部分节选如下: 让自己活得…...

SpringBoot帮你优雅的关闭WEB应用程序
Graceful shutdown 应用 Graceful shutdown说明 Graceful shutdown is supported with all four embedded web servers (Jetty, Reactor Netty, Tomcat, and Undertow) and with both reactive and servlet-based web applications. It occurs as part of closing the applica…...
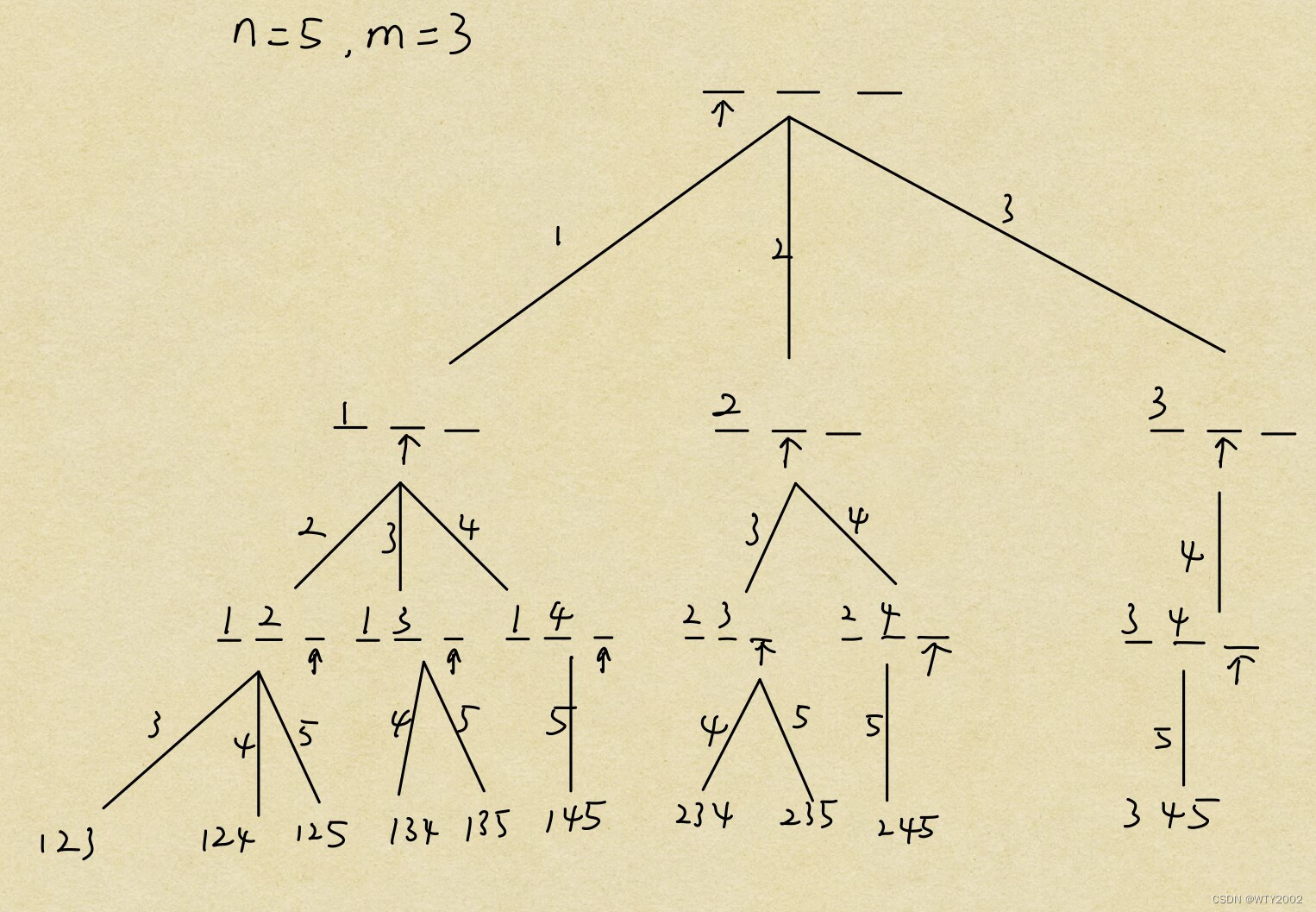
递归与递推
递归 直白理解:函数在其内部调用自身(自己调用自己)所有递归都可以采用递归搜索树来理解递归的特点: 一般来说代码较为简短,但是理解难度大一般时间和空间消耗较大,容易产生重复计算,可能爆栈 …...
使用<style scoped>导致的样式问题
问题描述: 今天使用开源组件库TDesign的自动补全组件时,遇到了一个样式失效问题,一开始怎么也找不到问题出在哪,后面一个偶然去掉了scoped,竟然发现样式竟然正常了,具体原因不知道在哪,有大佬知…...
-集群关键指标及调优指南)
Elasticsearch深入理解(十八)-集群关键指标及调优指南
1、CPU使用率 CPU使用率是指在一段时间内CPU执行程序的百分比,它是衡量系统资源利用率的一种指标。 1.1 详细说明: 在Elasticsearch中,高的CPU使用率通常意味着节点正在执行大量的计算任务,这可能是因为索引和搜索操作的负载较大…...
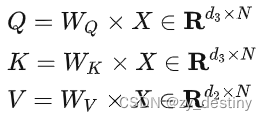
Transformer到底为何这么牛
从注意力机制(attention)开始,近两年提及最多的就是Transformer了,那么Transformer到底是什么机制,凭啥这么牛?各个领域都能用?一文带你揭开Transformer的神秘面纱。 目录 1.深度学习࿰…...

【Spring事务】声明式事务 使用详解
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 声明式事务一、编程式事务二、声明式事务&…...
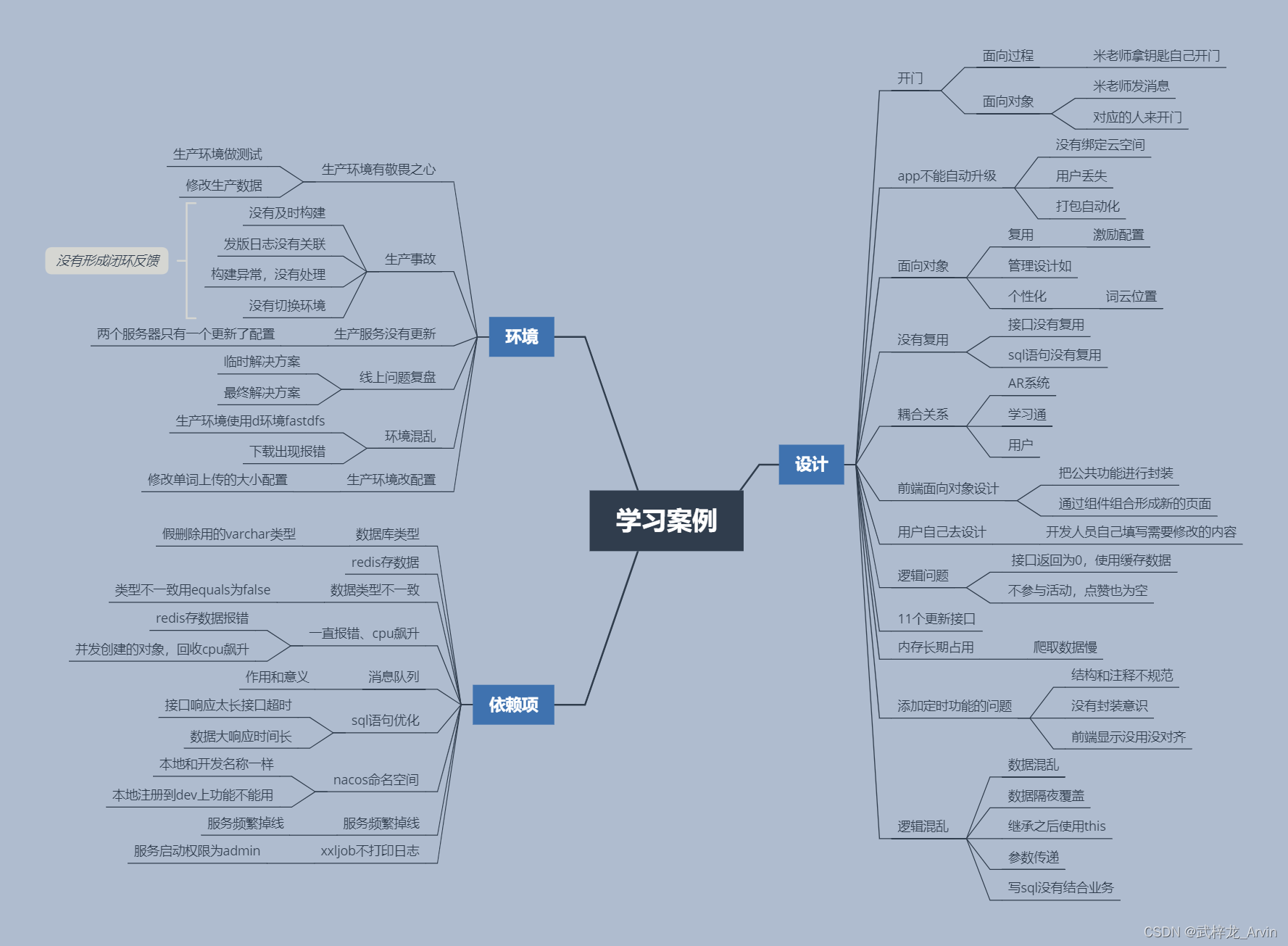
学习28个案例总结
学习前 对于之前遇到的问题没有及时总结,导致做什么事情都是新的一样。没有把之前学习到接触到的内容应用上。通过这次对28个案例的学习。把之前遇到的问题总结成自己的经验,在以后的开发过程中避免踩重复性的坑。多看帮助少走弯路。 学习中 对28个案例…...

刷题Java常用方法总结
刷题Java常用方法总结 文章目录刷题Java常用方法总结快速查看:静态数组 Static Array初始化instance属性length技巧Arrays.sort从小到大排序Arrays.fill填满一个数组Arrays.copyOf / arr.clone()复制一个数组(二维数组也可以)动态数组 List & Dynamic Array初始化常规 - Ar…...
大数据技术之Hive
第1章Hive基本概念1.1 Hive1.1.1 Hive的产生背景在那一年的大数据开源社区,我们有了HDFS来存储海量数据、MapReduce来对海量数据进行分布式并行计算、Yarn来实现资源管理和作业调度。但是面对海量数据和负责的业务逻辑,开发人员要编写MR来对数据进行统计…...

第33篇:Java集合类框架总结
目录 1、集合概念 2、集合与数组的区别 3、集合框架的特性 1)高性能 2)可操作...
数据结构 | 栈的中缀表达式求值
目录 什么是栈? 栈的基本操作 入栈操作 出栈操作 取栈顶元素 中缀表达式求值 实现思路 具体代码 什么是栈? 栈是一种线性数据结构,具有“先进后出”(Last In First Out, LIFO)的特点。它可以看作是一种受限的…...
vue2前端实现html导出pdf功能
1. 功能实现方案 1.html转换成canvas后生成图片导出pdf(本文选用) html转canvas插件:html2canvas是一款将HTML代码转换成Canvas的插件;canvas生成pdf:jsPDF是一个使用Javascript语言生成PDF的开源库 2.HTML代码转出…...

用 ChatGPT 辅助学好机器学习
文章目录一、前言二、主要内容🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 探索更高效的学习方法可能是有志者共同的追求,用好 ChatGPT,先行于未来。 作为一个人工智能大语言模型,ChatGPT 可以在帮助初…...
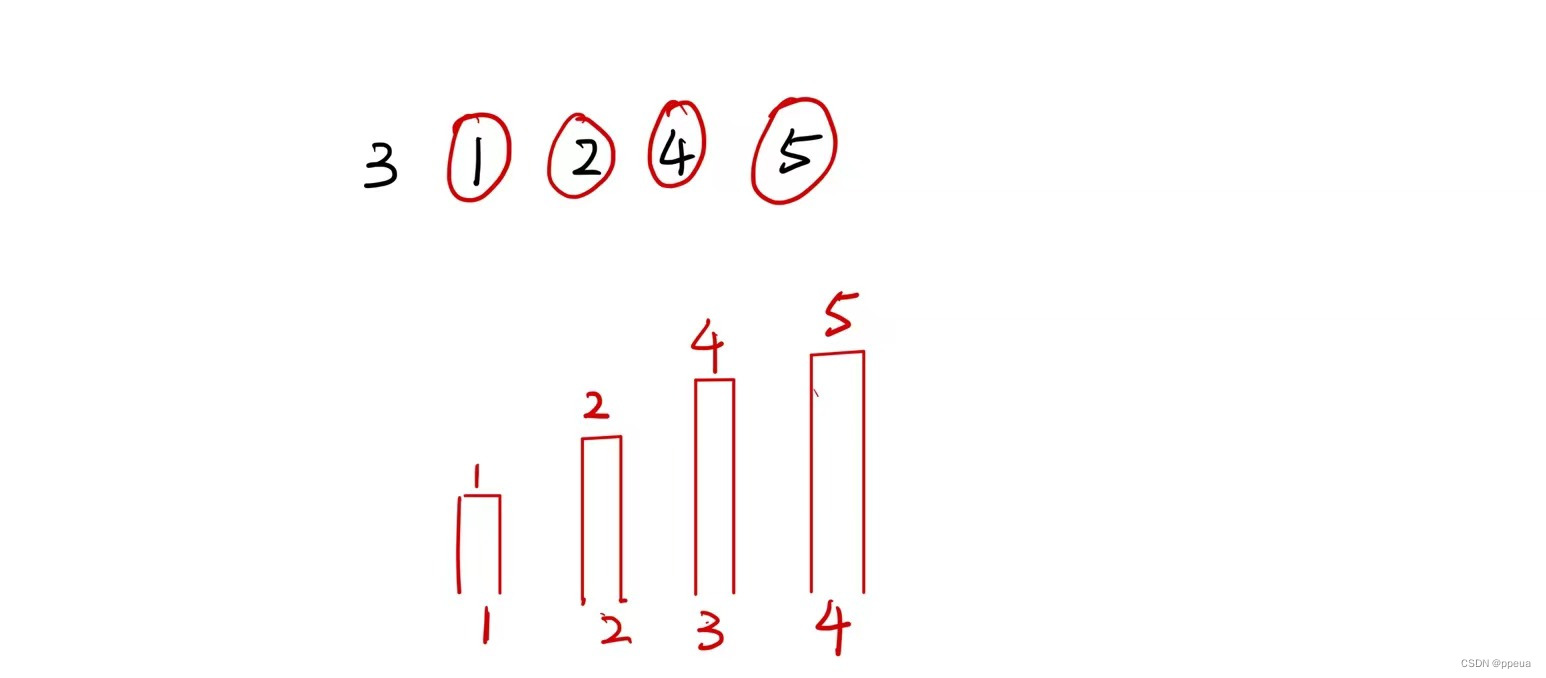
【动态规划】最长上升子序列(单调队列、贪心优化)
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
海思SD3403/SS928V100开发(7)mcp2515-SPI转CAN驱动开发
1. 前言 需求: 需要一路can进行收发 分析: 根据目前使用较多的方案是使用主控端SPI接口 接入MCP2515芯片进行CAN协议转换 硬件: MCP2515->SPI2->SS928 2. Uboot开发 2.1 pinmux复用配置 2.1.1 修改uboot参数表 路径: osdrv/tools/pc/uboot_tools/ SS928V100…...
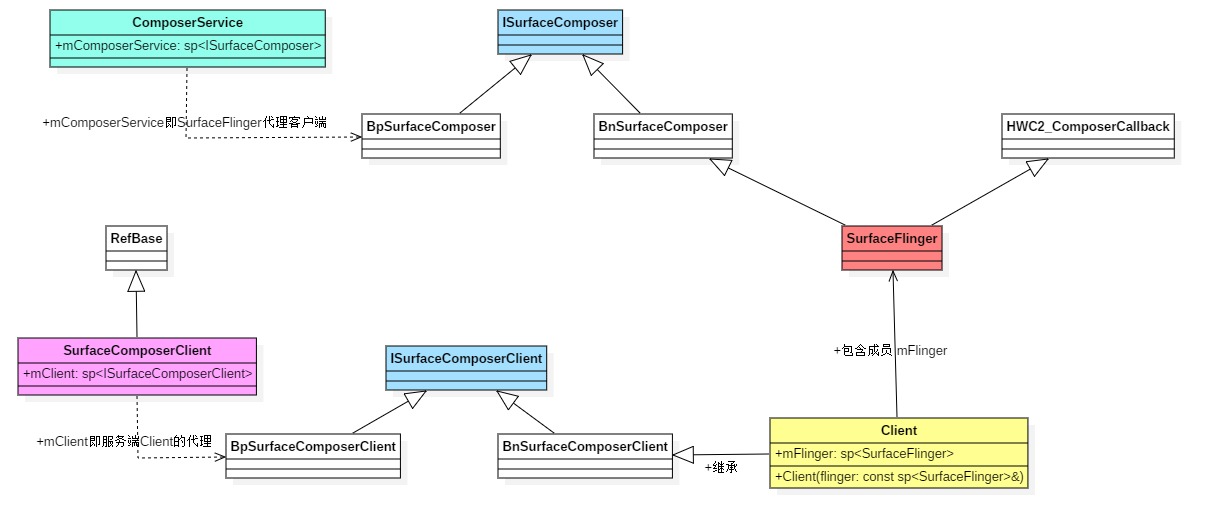
【安卓源码】SurfaceFlinger 启动及其与应用通信
1. surfaceFlinger 初始化和消息队列处理机制 surfaceflinger 的makefile 文件 /frameworks/native/services/surfaceflinger/Android.bp 235 cc_binary { 236 name: "surfaceflinger", 237 defaults: ["libsurfaceflinger_binary"], 238 i…...
springboot车辆充电桩
sprinboot车辆充电桩演示录像2022开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:ecli…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...