【蓝桥杯2020】七段码
【题目描述】
七段码 HUSTOJ 题目导出文件
[蓝桥杯2020] 第十一届蓝桥杯第二次省赛—填空题E题
七段码
小蓝要用七段码数码管来表示一种特殊的文字。
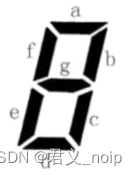
上图给出了七段码数码管的一个图示,数码管中一共有 7 段可以发光的二
极管,分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管(至少要有一个)发光来表达字符。在设计字符的表达时,要求所有发光的二极管是连成一片的。
例如:b 发光,其他二极管不发光可以用来表达一种字符。
例如:c 发光,其他二极管不发光可以用来表达一种字符。这种方案与上一行的方案可以用来表示不同的字符,尽管看上去比较相似。
例如:a, b, c, d, e 发光,f, g 不发光可以用来表达一种字符。
例如:b, f 发光,其他二极管不发光则不能用来表达一种字符,因为发光的二极管没有连成一片。请问,小蓝可以用七段码数码管表达多少种不同的字符?
【题目考点】
1. 深搜(子集树)
2. 图论 连通图(并查集,深搜)
【解题思路】
七段数码管中每个管是一个顶点,相邻的管之间有一条边,建立无向图:
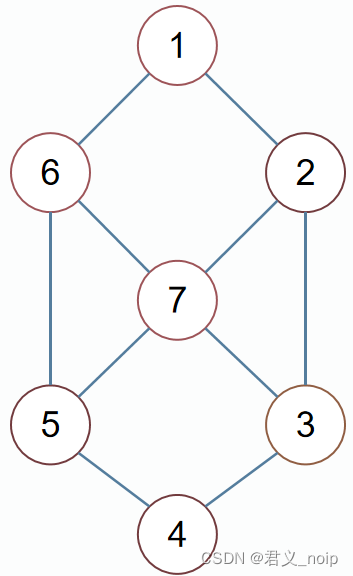
一些数码管亮,相当于在图中选择一些顶点,让这些顶点对应的数码管亮起,其它数码管不亮。要求选择的数码管连成一片,也就是选择的顶点和选择顶点之间的边构成的子图必须是连通图。
选择的顶点是所有顶点的子集,通过深搜子集树遍历每种可能的选择顶点的方案。
对于每种选择顶点的方案,判断选择的顶点,及选择顶点之间的边构成的子图是不是连通图。
判断一个图是否是连通图,可以使用并查集,也可以使用深搜的方法。
【题解代码】
答案:80
解法1:邻接矩阵 并查集判断连通图
#include<bits/stdc++.h>
using namespace std;
#define N 10
int fa[N], ans;
int edge[N][N];
bool sel[N];//sel[i]:管i亮了
void init(int n)
{for(int i = 1; i <= n; ++i)fa[i] = i;
}
int find(int x)
{if(fa[x] == x)return x;elsereturn fa[x] = find(fa[x]);
}
void merge(int x, int y)
{fa[find(x)] = find(y);
}
void addEdge(int u, int v)
{edge[u][v] = edge[v][u] = 1;
}
void initGraph()
{addEdge(1, 2);addEdge(2, 3);addEdge(3, 4);addEdge(4, 5);addEdge(5, 6);addEdge(6, 1);addEdge(6, 7);addEdge(5, 7);addEdge(2, 7);addEdge(3, 7);
}
bool check()//判断是否是连通图
{init(7);int ct = 0;for(int i = 1; i <= 7; ++i)for(int j = 1; j <= 7; ++j)if(edge[i][j] && sel[i] && sel[j])merge(i, j);for(int i = 1; i <= 7; ++i)if(fa[i] == i && sel[i])//管i亮着且是根结点 ct++;return ct == 1;
}
void dfs(int k)//管k是否亮
{if(k > 7){if(check())ans++;return;}dfs(k+1);sel[k] = true;dfs(k+1);sel[k] = false;
}
int main()
{init(7);initGraph();dfs(1);cout << ans;return 0;
}
解法2:邻接表 深搜判断连通图
#include<bits/stdc++.h>
using namespace std;
#define N 10
int ans;
vector<int> edge[N];
bool vis[N], sel[N];//sel[i]:管i亮了
void addEdge(int u, int v)
{edge[u].push_back(v);edge[v].push_back(u);
}
void initGraph()
{addEdge(1, 2);addEdge(2, 3);addEdge(3, 4);addEdge(4, 5);addEdge(5, 6);addEdge(6, 1);addEdge(6, 7);addEdge(5, 7);addEdge(2, 7);addEdge(3, 7);
}
void dfsGraph(int u)//对图做深搜
{for(int v : edge[u]){if(sel[v] && vis[v] == false)//注意只能访问已选择的顶点{vis[v] = true;dfsGraph(v);}}
}
bool check()//判断是否是连通图
{memset(vis, 0, sizeof(vis));int ct = 0;//连通分量个数 for(int v = 1; v <= 7; ++v){if(sel[v] && vis[v] == false){ct++;//连通分量个数增加1 vis[v] = true;dfsGraph(v);}}return ct == 1;//如果连通分量个数不为1,则不是连通图
}
void dfs(int k)//管k是否亮
{if(k > 7){if(check())ans++;return;}dfs(k+1);sel[k] = true;dfs(k+1);sel[k] = false;
}
int main()
{initGraph();dfs(1);cout << ans;return 0;
}
相关文章:

【蓝桥杯2020】七段码
【题目描述】 七段码 HUSTOJ 题目导出文件 [蓝桥杯2020] 第十一届蓝桥杯第二次省赛—填空题E题 七段码 小蓝要用七段码数码管来表示一种特殊的文字。 上图给出了七段码数码管的一个图示,数码管中一共有 7 段可以发光的二 极管,分别标记为 a, b, c,…...
Spark读取JDBC调优
Spark读取JDBC调优,如何调参一、场景构建二、参数设置1.灵活运用分区列实际问题:工作中需要读取一个存放了三四年历史数据的pg数仓表(缺少主键id),需要将数据同步到阿里云 MC中,Spark在使用JDBC读取关系型数…...

【文心一言】什么是文心一言,如何获得内测和使用方法。
文心一言什么是文心一言怎么获得内测资格接下来就给大家展示一下文学创作商业文案创作数理逻辑推算中文理解多模态生成用python写一个九九乘法表写古诗前言: 🏠个人主页:以山河作礼。 📝📝:本文章是帮助大家了解文心…...
CentOS8服务篇10:FTP服务器配置与管理
一、安装与启动FTP服务器 1、安装VSFTP服务器所需要的安装包 #yum -y install vsftpd 2、查看配置文件参数 Vim /etc/vsftpd/vsftpd.conf (1)是否允许匿名登录 anonymous_enableYES 该行用于控制是否允许匿名用户登录。 (2&…...

笔试强训3.14
一、选择题 1.以下说法错误的是(C) A.数组是一个对象 B.数组不是一种原生类 C.数组的大小可以任意改变 D.在Java中,数组存储在堆中连续内存空间里 相关知识点:原生/内置数组是那八个,其他的都是引用的,借…...

elasticsearch 环境搭建和基本操作
参考资料 适合后端编程人员的elasticsearch快速实战教程 ElasticSearch最新实战教程 ElasticSearch配套笔记 自制搜索引擎 https://www.elastic.co/guide/en/elasticsearch/reference/7.17/setup.html restful风格的api REST 设计风格 例如以下springboot示例 RestContr…...
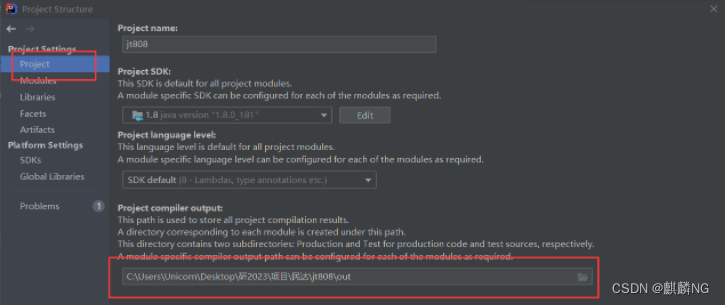
IDEA操作:Springboot项目打包为jar包并运行
在IDEA环境下对Springboot项目打包为jar包且在terminal运行操作 1、 2、 3、注意:在项目目录里创建一个用来存放jar包的文件夹(res),该路径不能使用IDEA设置的默认路径,必须手动创建。 4、 5、点击ok后加载运行包 (8…...
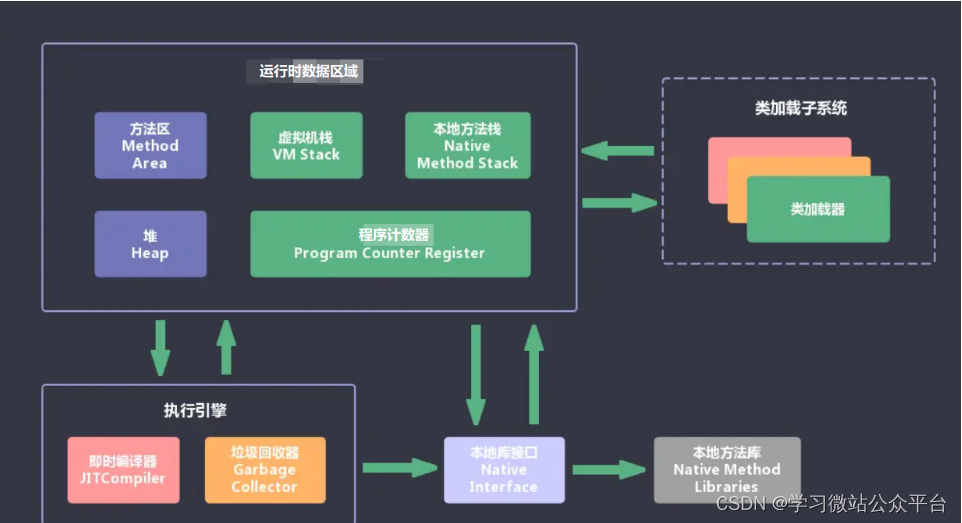
原理底层计划---JVM
二、JVM对空间大小怎么配置?各区域怎么划? 新生代:短时间生成,可以马上回收 老生代:少部分对象会存在很久,回收策略应不同 三、JVM哪些内存区域会发生内存溢出(程序计数器不会) …...

CSDN-猜年龄、纸牌三角形、排他平方数
猜年龄 原题链接:https://edu.csdn.net/skill/practice/algorithm-a413078fb6e74644b8c9f6e28896e377/2258 美国数学家维纳(N.Wiener)智力早熟,11岁就上了大学。他曾在1935~1936年应邀来中国清华大学讲学。 一次,他参加某个重要会议…...
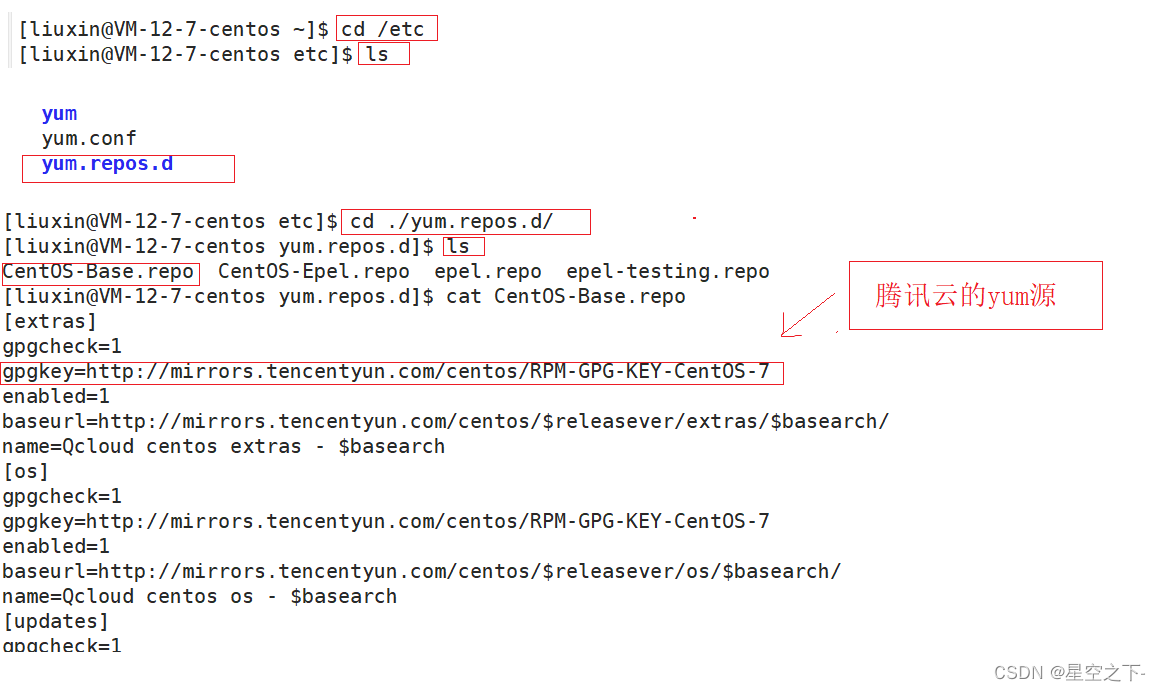
【Linux】软件包管理器 yum
什么是软件包和软件包管理器 在 Linux 下需要安装软件时, 最原始的办法就是下载到程序的源代码, 进行编译得到可执行程序。但是这样太麻烦了,所以有些人就把一些常用的软件提前编译好, 做成软件包 ( 就相当于windows上的软件安装程序)放在服…...
一天吃透TCP面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

zzu天梯赛选拔
C. NANA去上课 — 简单数学 需要记录上一步处在哪个位置 然后判断如果是同一侧移动距离就是abs(x1 - x2) 如果不同就是x1 x2 #include <iostream> #include <cmath> using namespace std; #define int long long signed main() {int n; c…...
【C语言】一篇让你彻底吃透(结构体与结构体位段)
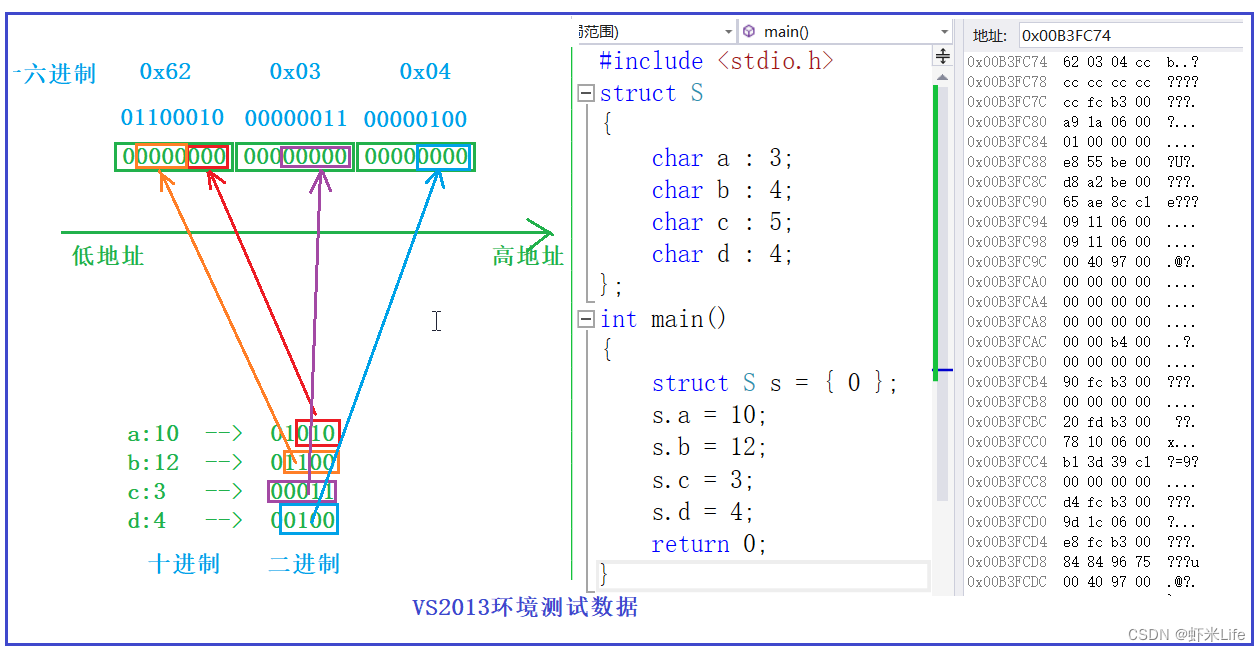
本章重点 主要讲解结构体和位移动的使用和定义与声明,并且结构体和位段在内存中是如何存储的。 文章目录结构体结构体类型的声明结构体特殊的声明结构体变量的定义和初始化结构体成员的访问结构的自引用结构体内存对齐结构体传参位段什么是位段位段的内存分配位段的…...

数据结构之二叉树构建、广度/深度优先(前序、中序、后序)遍历
一、二叉树 1.1 树 说到树,我们暂时忘记学习,来看一下大自然的树: 哈哈 以上照片是自己拍的,大家凑合看看 回归正题,那么在数据结构中,树是什么呢,通过上面的图片大家也可以理解 树是一种非…...

“国产版ChatGPT”文心一言发布会现场Demo硬核复现
文章目录前言实验结果一、文学创作问题1 :《三体》的作者是哪里人?问题2:可以总结下三体的核心内容吗?如果要续写的话,可以从哪些角度出发?问题3:如何从哲学角度来进行续写?问题4:电…...

202304读书笔记|《不被定义的女孩》——做最真实最漂亮的自己,依心而行
202304读书笔记|《不被定义的女孩》——做最真实最漂亮的自己,依心而行《不被定义的女孩》作者ASEN,很棒的书。处处透露着洒脱,通透,悦己,阅世界的自由的氛围和态度! 部分节选如下: 让自己活得…...

SpringBoot帮你优雅的关闭WEB应用程序
Graceful shutdown 应用 Graceful shutdown说明 Graceful shutdown is supported with all four embedded web servers (Jetty, Reactor Netty, Tomcat, and Undertow) and with both reactive and servlet-based web applications. It occurs as part of closing the applica…...
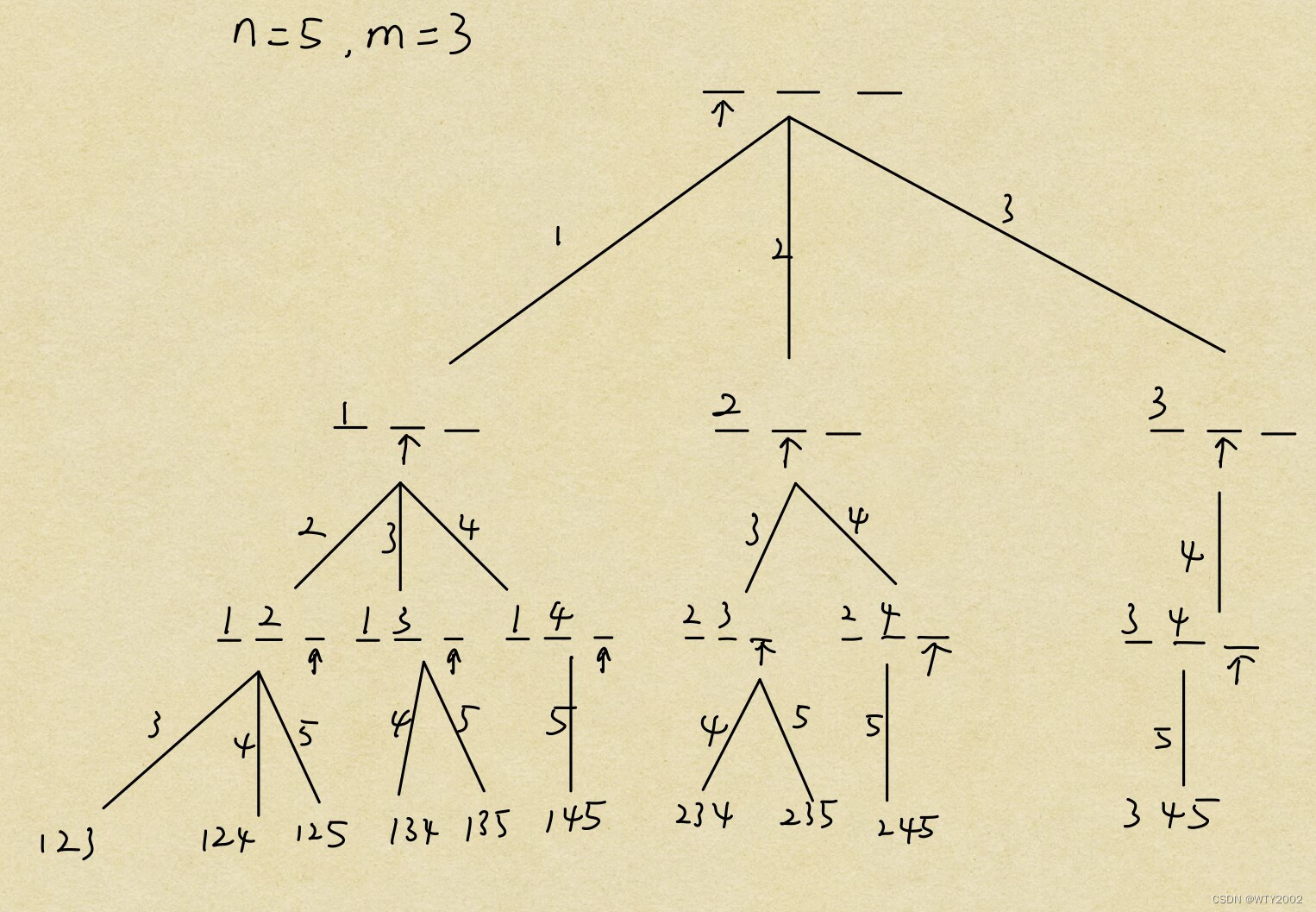
递归与递推
递归 直白理解:函数在其内部调用自身(自己调用自己)所有递归都可以采用递归搜索树来理解递归的特点: 一般来说代码较为简短,但是理解难度大一般时间和空间消耗较大,容易产生重复计算,可能爆栈 …...
使用<style scoped>导致的样式问题
问题描述: 今天使用开源组件库TDesign的自动补全组件时,遇到了一个样式失效问题,一开始怎么也找不到问题出在哪,后面一个偶然去掉了scoped,竟然发现样式竟然正常了,具体原因不知道在哪,有大佬知…...
-集群关键指标及调优指南)
Elasticsearch深入理解(十八)-集群关键指标及调优指南
1、CPU使用率 CPU使用率是指在一段时间内CPU执行程序的百分比,它是衡量系统资源利用率的一种指标。 1.1 详细说明: 在Elasticsearch中,高的CPU使用率通常意味着节点正在执行大量的计算任务,这可能是因为索引和搜索操作的负载较大…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
