CSDN-猜年龄、纸牌三角形、排他平方数
猜年龄
原题链接:https://edu.csdn.net/skill/practice/algorithm-a413078fb6e74644b8c9f6e28896e377/2258
美国数学家维纳(N.Wiener)智力早熟,11岁就上了大学。他曾在1935~1936年应邀来中国清华大学讲学。
一次,他参加某个重要会议,年轻的脸孔引人注目。于是有人询问他的年龄,他回答说:“我年龄的立方是个4位数。我年龄的4次方是个6位数。这10个数字正好包含了从0到9这10个数字,每个都恰好出现1次。”
请你推算一下,他当时到底有多年轻。
提示:
先用/10和%10把各个位上的数取出来,然后判断是否相等
官方题目是没给代码的,直接给了年龄作为选项
于是我们自己写一个
#include <iostream>
#include <set>int main() {std::set<int>st;for (int i = 11; i < 100; i++) {//我的年龄的立方是个四位数if (i * i * i > 1000) {//我年龄的4次方是个6位数if (i * i * i * i > 100000) {//这10个数字正好包含了从0到9这10个数字,每个都恰好出现1次//把每位数字塞进set中,判断元素个数是否为10int tmp = i * i * i * i;while (tmp > 0) {st.insert(tmp % 10);tmp /= 10;}tmp = i * i * i;while (tmp > 0) {st.insert(tmp % 10);tmp /= 10;}if (st.size() == 10) {std::cout << i << std::endl;break;}}}}return 0;
}
简单粗暴的算法,代码中带了注释,在此不再赘述。
需要注意的是,要及时跳出。
纸牌三角形
原题链接:https://edu.csdn.net/skill/practice/algorithm-aa21244fb1374002acf29ed59bee7978/2391
A, 2, 3, 4, 5, 6, 7, 8, 9 共9张纸牌排成一个正三角形(A按1计算)。要求每个边的和相等。
下面就是一种排法
A9 64 8
3 7 5 2
这样的排法可能会有很多。
如果考虑旋转、镜像后相同的算同一种,一共有多少种不同的排法呢?
以下程序实现了这一功能,请你补全以下空白处内容:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{int a[9] = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };int res = 0;do{int x1 = a[0] + a[1] + a[2] + a[3];int x2 = a[3] + a[4] + a[5] + a[6];int x3 = a[6] + a[7] + a[8] + a[0];__________________;} while (next_permutation(a, a + 9));cout << res / 3 / 2 << endl;return 0;
}
提示:
1、正三角形有三个角,所以一个数字可以在三个角各出现一次,这就相当于旋转。
2、在生活中你照镜子的时候会发现,当你抬起左手时,你会看到镜子中的你会抬起右手。在本题中滤镜前后包括一个正三角形和该正三角形左右位置对称交换后的正三角形
需要用到全排列函数,呈上cplusplus的官方示例
// next_permutation example
#include <iostream> // std::cout
#include <algorithm> // std::next_permutation, std::sortint main () {int myints[] = {1,2,3};std::sort (myints,myints+3);std::cout << "The 3! possible permutations with 3 elements:\n";do {std::cout << myints[0] << ' ' << myints[1] << ' ' << myints[2] << '\n';} while ( std::next_permutation(myints,myints+3) );std::cout << "After loop: " << myints[0] << ' ' << myints[1] << ' ' << myints[2] << '\n';return 0;
}
全排列函数
对于next_permutation函数,其函数原型为:
#include <algorithm>
bool next_permutation(iterator start,iterator end)
当当前序列不存在下一个排列时,函数返回false,否则返回true
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {vector<int>vec;vec.push_back(1);vec.push_back(2);vec.push_back(3);do {cout << vec[0] << " " << vec[1] << " " << vec[2] << endl;} while (next_permutation(vec.begin(), vec.end()));cout << vec[0] << " " << vec[1] << " " << vec[2] << endl;return 0;
}
如果使用do...while则会显示所有可能的全排列方法。上面的例子是6种排列。
如果使用while则会省略初识的第一种排列方法。上面的例子将变为5种排列。
全排列函数会考虑数据相同的元素,不会产生完全重复的排列方式。
在跳出循环后,迭代器会回到全排列之前的状态。
回到题目
题中的while就是个全排列。
然后求全排列后的各边长。
划线的部分就是用来判断是否符合条件。
正确答案
if (x1 == x2 && x2 == x3)
{res++;
}
题目要求避免旋转和翻转之后的重复情况,而题目中循环内没有去重的部分。
因此去重放在了循环外。
cout << res / 3 / 2 << endl;
- res是所有可能的排列,没有去重。
- 三条边两两互换,有三种实际上相同的可能,需要
/3。 - 每条边内,
a[0]和a[3]互换,又会出现两种可能,需要/2。
排他平方数
原题链接:https://edu.csdn.net/skill/practice/algorithm-ef16a8876b2446c0981c5b9cf28f278d/2314
203879 * 203879 = 41566646641
这有什么神奇呢?仔细观察,203879 是个6位数,并且它的每个数位上的数字都是不同的,并且它平方后的所有数位上都不出现组成它自身的数字。
具有这样特点的6位数还有一个,请你找出它!
再归纳一下筛选要求:
- 6位正整数。
- 每个数位上的数字不同。
- 其平方数的每个数位不含原数字的任何组成数位。
以下程序实现了这一功能,请你补全以下空白处内容:
#include <iostream>
using namespace std;int main()
{int num[10], flag;for (long long i = 123456; i <= 987654; i++){long long a = i;long long b = i * i;memset(num, 0, sizeof(num));flag = 1;while (a){_________________;}if (flag){while (b){if (num[b % 10]){flag = 0;break;}b /= 10;}if (flag)cout << i << endl;}}return 0;
}
正确答案
if (num[a % 10])
{flag = 0;break;
}
num[a % 10]++;
a /= 10;
逐行分析一下
for (long long i = 123456; i <= 987654; i++)
题目要求六位数的各位都不相同。
循环从符合条件的最小六位数123456遍历到最大六位数987654。
long long a = i;
long long b = i * i;
分别定义a、b两个变量来存储该六位数和该六位数的平方。
memset(num, 0, sizeof(num));
将循环外定义的数组的内存数据设置为0,用于存储整型各位上的值。
flag = 1;
初始化一个标记,默认值为1。用于在之后的函数中判断走向。如果后面的函数中发现不符合条件,则赋值为0,并执行flag==0时的语句。
while (a)内的语句。
取a的最后一位,并砍掉a的最后一位,修改num数组中存储的个数。
如果添加时发现已存储的个数大于0,说明不符合“不重复”的条件,可以直接跳出循环,同时修改flag标记,快速跳出后面的语句。
如果检测到a已经为0,则跳出循环,执行后面的语句。
if (flag)
flag作为循环条件。是因为上一步的break只能跳出所在的最内层while循环。不符合条件不能直接跳两层,所以使用flag快速跳出。
while (b)
与while(a)语句类似,但删掉了num[a % 10]++;语句,是因为题干没有要求平方后的数值内部不能有重复。只需要比较b的各位上的数不与a重复即可。
如果不符合条件,则修改标记flag等于0。
if (flag)
前面的每一步中,每有不符合条件的情况,都会修改标记为0。
到这一步时,如果flag值为1,说明符合条件,则输出对应的i值。
相关文章:

CSDN-猜年龄、纸牌三角形、排他平方数
猜年龄 原题链接:https://edu.csdn.net/skill/practice/algorithm-a413078fb6e74644b8c9f6e28896e377/2258 美国数学家维纳(N.Wiener)智力早熟,11岁就上了大学。他曾在1935~1936年应邀来中国清华大学讲学。 一次,他参加某个重要会议…...
【Linux】软件包管理器 yum
什么是软件包和软件包管理器 在 Linux 下需要安装软件时, 最原始的办法就是下载到程序的源代码, 进行编译得到可执行程序。但是这样太麻烦了,所以有些人就把一些常用的软件提前编译好, 做成软件包 ( 就相当于windows上的软件安装程序)放在服…...
一天吃透TCP面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

zzu天梯赛选拔
C. NANA去上课 — 简单数学 需要记录上一步处在哪个位置 然后判断如果是同一侧移动距离就是abs(x1 - x2) 如果不同就是x1 x2 #include <iostream> #include <cmath> using namespace std; #define int long long signed main() {int n; c…...
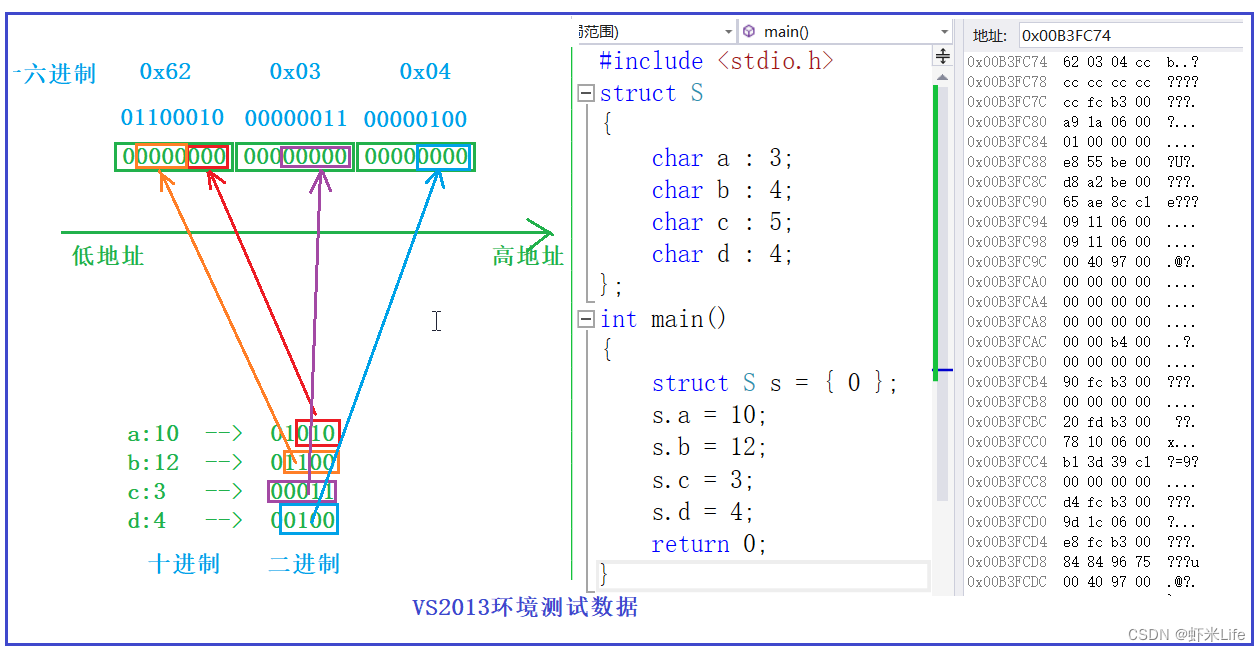
【C语言】一篇让你彻底吃透(结构体与结构体位段)
本章重点 主要讲解结构体和位移动的使用和定义与声明,并且结构体和位段在内存中是如何存储的。 文章目录结构体结构体类型的声明结构体特殊的声明结构体变量的定义和初始化结构体成员的访问结构的自引用结构体内存对齐结构体传参位段什么是位段位段的内存分配位段的…...

数据结构之二叉树构建、广度/深度优先(前序、中序、后序)遍历
一、二叉树 1.1 树 说到树,我们暂时忘记学习,来看一下大自然的树: 哈哈 以上照片是自己拍的,大家凑合看看 回归正题,那么在数据结构中,树是什么呢,通过上面的图片大家也可以理解 树是一种非…...

“国产版ChatGPT”文心一言发布会现场Demo硬核复现
文章目录前言实验结果一、文学创作问题1 :《三体》的作者是哪里人?问题2:可以总结下三体的核心内容吗?如果要续写的话,可以从哪些角度出发?问题3:如何从哲学角度来进行续写?问题4:电…...

202304读书笔记|《不被定义的女孩》——做最真实最漂亮的自己,依心而行
202304读书笔记|《不被定义的女孩》——做最真实最漂亮的自己,依心而行《不被定义的女孩》作者ASEN,很棒的书。处处透露着洒脱,通透,悦己,阅世界的自由的氛围和态度! 部分节选如下: 让自己活得…...

SpringBoot帮你优雅的关闭WEB应用程序
Graceful shutdown 应用 Graceful shutdown说明 Graceful shutdown is supported with all four embedded web servers (Jetty, Reactor Netty, Tomcat, and Undertow) and with both reactive and servlet-based web applications. It occurs as part of closing the applica…...
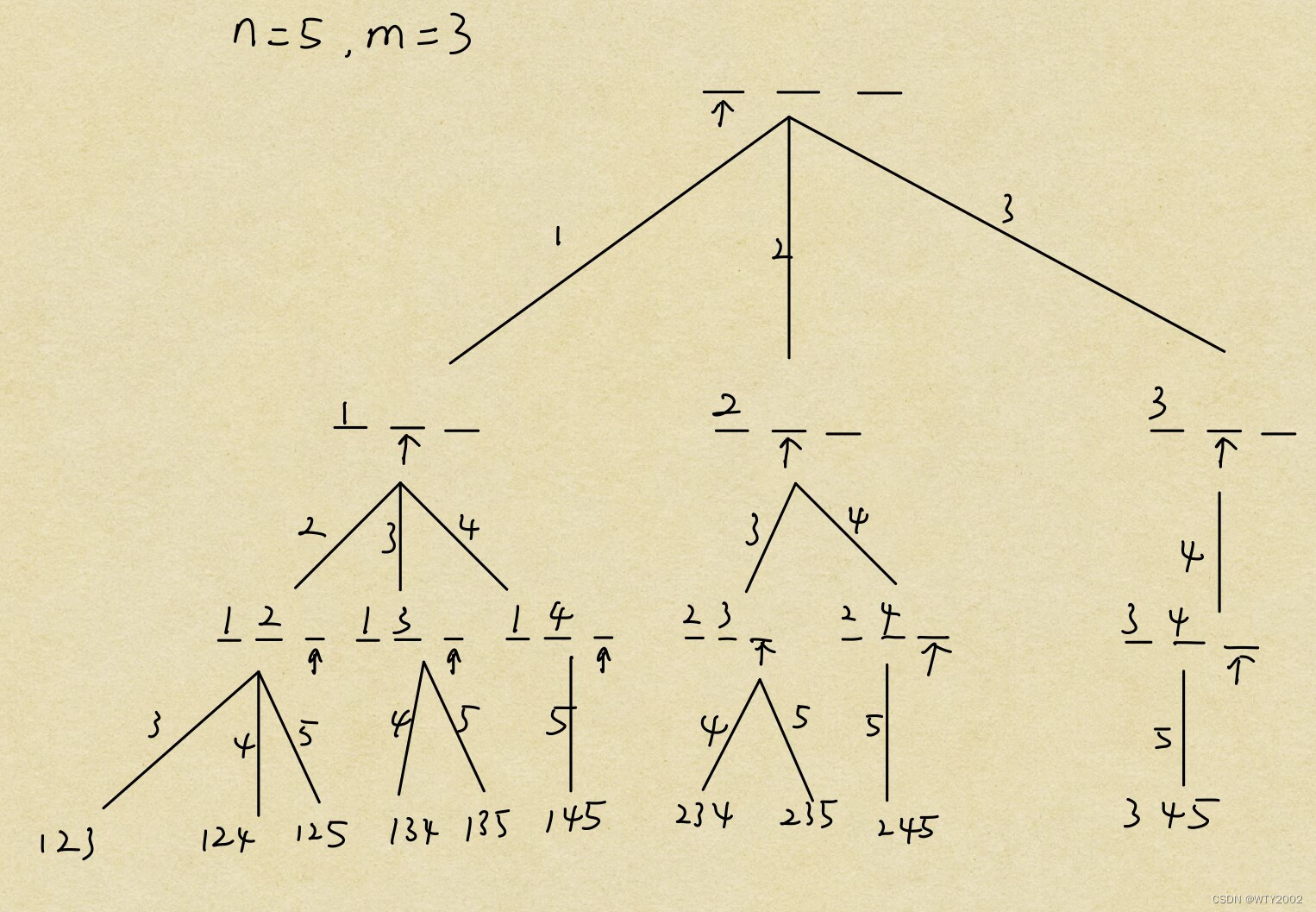
递归与递推
递归 直白理解:函数在其内部调用自身(自己调用自己)所有递归都可以采用递归搜索树来理解递归的特点: 一般来说代码较为简短,但是理解难度大一般时间和空间消耗较大,容易产生重复计算,可能爆栈 …...
使用<style scoped>导致的样式问题
问题描述: 今天使用开源组件库TDesign的自动补全组件时,遇到了一个样式失效问题,一开始怎么也找不到问题出在哪,后面一个偶然去掉了scoped,竟然发现样式竟然正常了,具体原因不知道在哪,有大佬知…...
-集群关键指标及调优指南)
Elasticsearch深入理解(十八)-集群关键指标及调优指南
1、CPU使用率 CPU使用率是指在一段时间内CPU执行程序的百分比,它是衡量系统资源利用率的一种指标。 1.1 详细说明: 在Elasticsearch中,高的CPU使用率通常意味着节点正在执行大量的计算任务,这可能是因为索引和搜索操作的负载较大…...
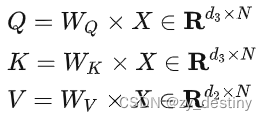
Transformer到底为何这么牛
从注意力机制(attention)开始,近两年提及最多的就是Transformer了,那么Transformer到底是什么机制,凭啥这么牛?各个领域都能用?一文带你揭开Transformer的神秘面纱。 目录 1.深度学习࿰…...

【Spring事务】声明式事务 使用详解
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 声明式事务一、编程式事务二、声明式事务&…...
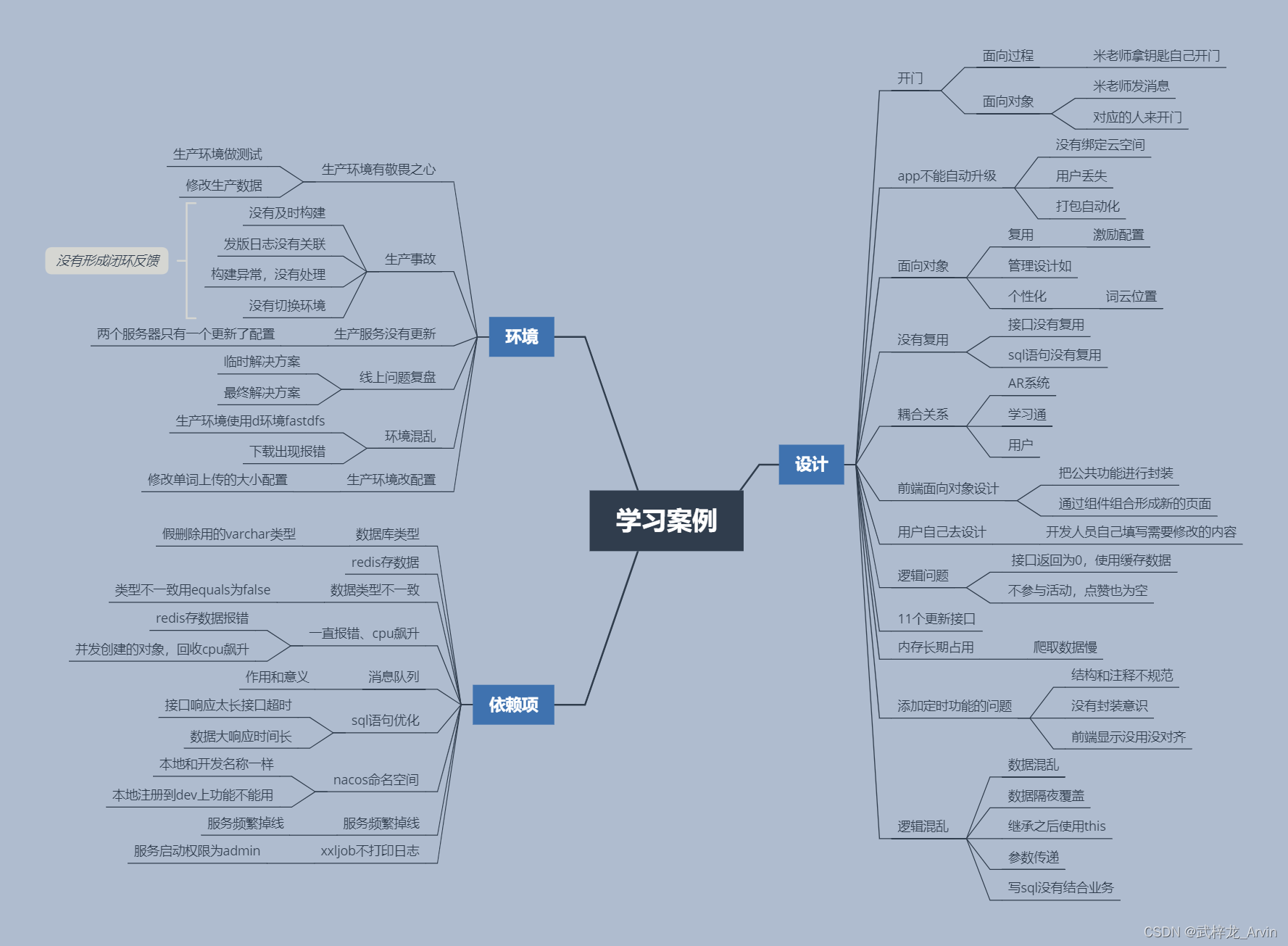
学习28个案例总结
学习前 对于之前遇到的问题没有及时总结,导致做什么事情都是新的一样。没有把之前学习到接触到的内容应用上。通过这次对28个案例的学习。把之前遇到的问题总结成自己的经验,在以后的开发过程中避免踩重复性的坑。多看帮助少走弯路。 学习中 对28个案例…...

刷题Java常用方法总结
刷题Java常用方法总结 文章目录刷题Java常用方法总结快速查看:静态数组 Static Array初始化instance属性length技巧Arrays.sort从小到大排序Arrays.fill填满一个数组Arrays.copyOf / arr.clone()复制一个数组(二维数组也可以)动态数组 List & Dynamic Array初始化常规 - Ar…...
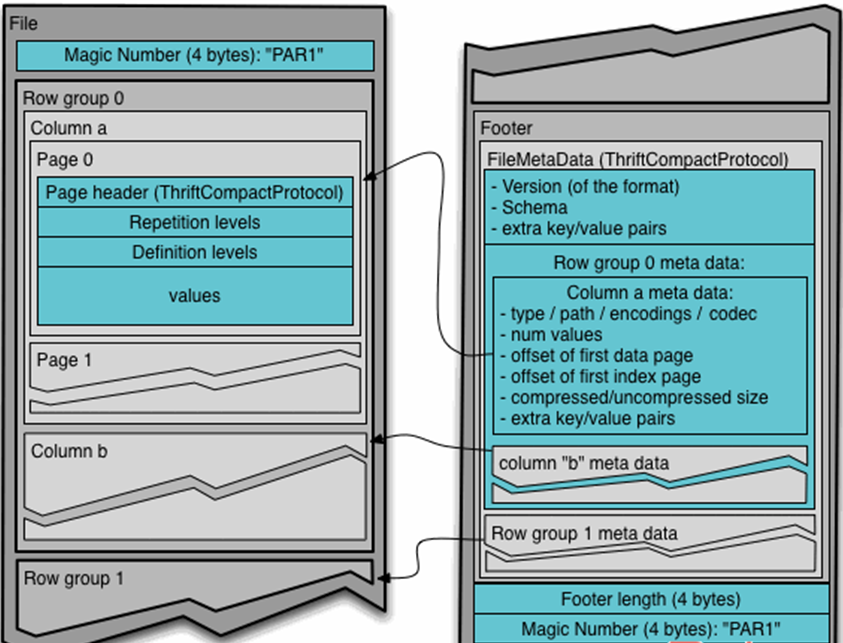
大数据技术之Hive
第1章Hive基本概念1.1 Hive1.1.1 Hive的产生背景在那一年的大数据开源社区,我们有了HDFS来存储海量数据、MapReduce来对海量数据进行分布式并行计算、Yarn来实现资源管理和作业调度。但是面对海量数据和负责的业务逻辑,开发人员要编写MR来对数据进行统计…...

第33篇:Java集合类框架总结
目录 1、集合概念 2、集合与数组的区别 3、集合框架的特性 1)高性能 2)可操作...
数据结构 | 栈的中缀表达式求值
目录 什么是栈? 栈的基本操作 入栈操作 出栈操作 取栈顶元素 中缀表达式求值 实现思路 具体代码 什么是栈? 栈是一种线性数据结构,具有“先进后出”(Last In First Out, LIFO)的特点。它可以看作是一种受限的…...
vue2前端实现html导出pdf功能
1. 功能实现方案 1.html转换成canvas后生成图片导出pdf(本文选用) html转canvas插件:html2canvas是一款将HTML代码转换成Canvas的插件;canvas生成pdf:jsPDF是一个使用Javascript语言生成PDF的开源库 2.HTML代码转出…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
