(数据结构)八大排序算法
目录
- 一、常见排序算法
- 二、实现
- 1. 直接插入排序
- 2.🌟希尔排序
- 3. 选择排序
- 4.🌟堆排序
- 5. 冒泡排序
- 7. 🌟快速排序
- 7.1 其他版本的快排
- 7.2 优化
- 7.3 ⭐非递归
- 7. 🌟归并排序
- 7.1 ⭐非递归
- 8. 计数排序
- 三、总结
- 1. 分析
排序 (Sorting) 是计算机程序设计中的一种重要操作,它的功能是将一个 数据元素 (或记录)的任意序列,重新排列成一个关键字有序的序列。
一、常见排序算法

二、实现
1. 直接插入排序
介绍:将待排的数,和有序的数比较,直到一个合适的位置,然后进行插入。
示图:
将待排数4,与有序数对比,然后插入到(比4小的数)2前面
代码:
// 插入排序(升序)
void InsertSort(int* a, int n)
{for (int i = 0; i < n-1 ; ++i){int end = i;//[0,end]为有序数组//记录下需要插入的数,将end+1的位置空出来int temp = a[end + 1];//将需插入的数和有序数组对比while (end >= 0){//如果大于,则向后移动一位if (a[end] > temp){a[end + 1] = a[end];end--;}else//否则,退出{break;}}//下标(end+1)就是合适的插入位置a[end + 1] = temp;}
}
效率:时间复杂度为 O(N2)O(N^2)O(N2)
如果原始数组为升序有序,则直接会break,时间复杂度为O(N)O(N)O(N)。
2.🌟希尔排序
介绍:利于直接插入排序的思想,如果所排的数据接近有序,则排序效率非常高。希尔排序,是将数据非为若干组,然后对每组的数据进行插入排序,使之逐渐有序。
其中如果分组为1,则等于直接插入排序
图示:
将数据分为9 5 8 1和3 2 7两组,分别进行插入排序,得到1 2 5 3 8 7 9,逐渐接近有序
代码:
void Swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}
// 希尔排序(升序)
void ShellSort(int* a, int n)
{int group = n;//逐渐将分组缩小,直至分组为1while (group > 1){//一般分组每次缩小1/3//+1:为确保最后分组为1group = group / 3 + 1;//每个数依次在它所在组中插入排序for (int i = 0; i < n - group; i++){int end = i;//每组排序好的最后一个元素int temp = a[end + group];//对应组下一个要插入的元素//思路同插入排序,只不过操作的是对应组中的元素while (end >= 0){if (a[end] > temp){a[end + group] = a[end];end -= group;}else{break;}}a[end + group] = temp;}}
}
效率:时间复杂度大约为 O(N1.3)O(N^{1.3})O(N1.3)
因为希尔排序的时间复杂度非常难算,感兴趣的可以去百度。
3. 选择排序
介绍:每一次都遍历一遍数据,选出最小(大)的元素,放在起始点。
图示:
代码:
// 选择排序(升序)
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;//每遍历一遍,选出最大和最小while (begin < end){int maxi = end;int mini = begin;for (int i = begin; i <= end; i++){if (a[maxi] < a[i]){maxi = i;}if (a[mini] > a[i]){mini = i;}}Swap(&a[begin], &a[mini]);//如果最大的数下标为begin,被上一步改变if (maxi == begin){maxi = mini;}Swap(&a[end], &a[maxi]);begin++;end--;}
}
效率:时间复杂度为O(N2)O(N^2)O(N2)
虽然一次遍历找一个,优化为每趟找两个,只是每趟比较次数的等差数列的公差由1变为2,但是大OOO的渐进表示法都为O(N2)O(N^2)O(N2)
4.🌟堆排序
简介:该部分涉及堆的相关知识,
详情请见另一篇:堆
效率:时间复杂度为O(Nlog2N)O(Nlog_2N)O(Nlog2N)
5. 冒泡排序
简介:冒泡的思想就是遍历数据进行比较,然后把最大(小)的数交换到最后位置。
图示:
代码:
// 冒泡排序(升序)
void BubbleSort(int* a, int n)
{//最多要遍历n-1次for (int i = 0; i < n - 1; ++i){int flag = 0;for (int j = 0; j < n - i - 1; ++j){//当前的数与下一个数进行比较if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);flag = 1;}}//如果没有进行交互,则已经排序完成了if (flag == 0){break;}}
}
效率:时间复杂度O(N2)O(N^2)O(N2)
因为优化了退出条件,因此对于已排序的原始数据,时间复杂度为O(N)O(N)O(N)
7. 🌟快速排序
简介:开始时,任取数据中的某一元素为基准,然后将小于该元素的放在左边,大于该元素的放在右边,把剩余数据分为两个序列。然后再对左右序列重复该过程,直到每个元素都在对应位置
(hoare版本)图示:
对数组4 3 6 7 2 1 5,以第一个4为关键数,升序排列,大于4的都放在右边,小于4的放在左边。得到结果2 3 1 4 6 7 5
先移动右指针,走到小于4的数停下,再移动左指针,找到大于4的数停下,交换两数,然后继续,直到左右指针相遇,因为左指针后走,因此停下的位置一定是小于等于4的,再和4交换。
代码:
void QuickSort(int* a, int left, int right)
{//如果只有一个数,直接返回if (left >= right){return;}//记录起始和结束int begin = left;int end = right;//默认key为第一个数int keyi = left;while (left < right){//先移动右指针,找到比key小的数while (left < right && a[right] >= a[keyi]){right--;}//再移动左指针,找到比key大的数while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}//right位置一定小于等于keyi位置数据Swap(&a[right], &a[keyi]);keyi = right;//分别排左右序列//[left,keyi-1], keyi, [keyi-1,right]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}
效率:时间复杂度O(Nlog2N)O(Nlog_2N)O(Nlog2N)。每次走一趟,一共走log2Nlog_2Nlog2N次
7.1 其他版本的快排
挖坑法:

void QuickSort(int* a, int left, int right)
{if (left >= right) return;int begin = left, end = right;//默认key为第一个数int key = a[left];int piti = left;//坑的位置while (left < right){//右指针先走while (left < right && a[right] >= key){--right;}a[piti] = a[right];piti = right;//左指针走while (left < right && a[left] <= key){++left;}a[piti] = a[left];piti = left;}//最后留下的坑位来存放keya[piti] = key;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}
前后指针:
用cur来找到小于key的元素,prev找到大于key的元素。刚开始时,cur还未遇见大于等于key的元素时,cur和prev一起向右。(如果此步,不好理解的话,可以自己动手画画)
void QuickSort(int* a, int left, int right)
{if (left >= right) return;int begin = left, end = right; int keyi = left; //默认key为第一个数int prev = left;int cur = left + 1;while (cur <= right){//当cur小于key,且prev++后不等于cur,才会交换if (a[cur] < a[keyi] && ++prev!=cur){Swap(&a[cur], &a[prev]);}++cur;//cur一直向后走}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}
7.2 优化
三数取中:
因为key的选取会影响快速排序的效率,其中,如果key每次都是是中间的数,接近二分,效率最高O(Nlog2N)O(Nlog_2N)O(Nlog2N);如果每次都是最小(大)的数,则效率最低O(N2)O(N^2)O(N2),因为总会出现[key]+[未排序数据]
//找到前中后三个数中,中间的那个
int GetMid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[mid] < a[left]){if (a[right] > a[left]){return left;}else if (a[right] < a[mid]){return mid;}else{return right;}}else{if (a[right] < a[left]){return left;}else if (a[right] > a[mid]){return mid;}else{return right;}}
}
结合插入排序:
对于一组比较大的数据,在递归后期,小范围的序列会有很多。因此可以在划分的范围足够小后,直接使用插入排序,避免继续向下递归。(tips:最后一次的递归次数占总递归次数的一半左右)
void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = left;int end = right;//三数取中int midi = GetMid(a, left, right);Swap(&a[midi], &a[keyi]);//使用插入排序if (right - left < 13){InsertSort(a + left, right - left + 1);}else{int begin = left, end = right;while (left < right){//先移动右指针,找到比key小的数while (left < right && a[right] >= a[keyi]){right--;}//再移动左指针,找到比key大的数while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[right], &a[keyi]);keyi = right;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}
7.3 ⭐非递归
递归的思想,比较容易写,但是它占用栈区空间,如果数据足够大,是可能发生栈溢出错误的。
保持快速排序的思路不变,显然循环无法实现,但是我们可以用栈来模拟递归。
每次将要比较的序列的范围[bigin,end],记录到栈中,每次循环开始,出栈,结束后又将新划分的左右序列入栈。
快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{Stack st;StackInit(&st);StackPush(&st, left);StackPush(&st, right);while (!StackEmpty(&st)){//出栈,得到要排序的范围[bigin,end]int end = StackTop(&st);StackPop(&st);int begin = StackTop(&st);StackPop(&st);//排序,使key放到正确位置int keyi = begin;int prev = begin;int cur = begin + 1;while (cur <= end){//当cur小于key,且prev++后不等于cur,才会交换if (a[cur] < a[keyi] && ++prev!=cur){Swap(&a[cur], &a[prev]);}++cur;//cur一直向后走}Swap(&a[keyi], &a[prev]);keyi = prev;//将新的左右序列[bigin,keyi-1],[keyi+1,end]入栈if (begin < keyi - 1){StackPush(&st, begin);StackPush(&st, keyi - 1);}if (keyi + 1 < end){StackPush(&st, keyi + 1);StackPush(&st, end);}}StackDestroy(&st);
}
同样的,其实可以用队列来实现快速排序的非递归。
思路:将bigen end入队列,循环开始时,出队列找到要排序的范围[begin,end],排序完成后将左右序列[bigin,keyi-1],[keyi+1,end]入队列
和栈实现不同的是:栈是以递归的方式,排完左序列后才会开始排右,而队列则是排左,排右交替进行。
7. 🌟归并排序
简介:采用分治实现,将数据划分为两等份分别有序的序列,然后合并。
图示:
对数据1 0 5 3 2,进行归并排序,首先将数据分为两份1 0 5和3 2,在向下划分,直至最小的,然后在将两两归并,逐渐形成有序序列。
代码:
void _MergeSort(int* a, int n, int begin, int end, int* temp)
{if (begin >= end){return;}int mid = (begin + end) / 2;
//由图示,可见,后序,深度优先//[begin,mid] [mid+1,end]_MergeSort(a, n, begin, mid, temp);_MergeSort(a, n, mid+1, end, temp);//将[begin,mid] [mid+1,end]两个序列按顺序合并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){// "<"升序if (a[begin1] < a[begin2]){temp[i++] = a[begin1++];}else{temp[i++] = a[begin2++];}}//处理某个序列的剩余数据while (begin1 <= end1){temp[i++] = a[begin1++];}while (begin2 <= end2){temp[i++] = a[begin2++];}//拷贝到原数组中,也可以使用库函数
//memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));for (int j = begin; j <= end; ++j){a[j] = temp[j];}}// 归并排序递归实现
void MergeSort(int* a, int n)
{//因为有两个序列归并一起,因此需要额外的空间存放,temp为额外空间int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc failed\n");exit(-1);}_MergeSort(a, n, 0, n - 1, temp);free(temp);
}
效率:时间复杂度O(Nlog2N)O(Nlog_2N)O(Nlog2N)
严格的二分,会比快速排序更优,但是需要额外的空间O(N)O(N)O(N)
7.1 ⭐非递归
递归,同样面临栈溢出的风险。
由归并排序的思想,先将数据划分为1个数一组的序列,然后将相邻的两个组合并,然后再分为2个数一组的序列,再进行合并,直到最后划分整个序列为一组。
tips:由于是按照1,2,4,8…逐渐划分的,但是原始数据的长度可能并不是严格的2n2^n2n个,所有划分出的组可能会出现越界问题,需要处理。
代码:
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{//需要的额外空间int* temp = (int*)malloc(sizeof(int) * n);int grap = 1;//开始时一组有1个数while (grap < n){//[j,j+grap-1] 与 [j+grap,j+2*grap-1] 按序合并for (int j = 0; j < n; j += grap*2){int begin1 = j, end1 = j+grap-1;int begin2 = j + grap, end2 = j + 2 * gap - 1;//修正//end1数组越界if (end1 >= n){end1 = n - 1;begin2 = n;end2 = n - 1;}//begin2数组越界else if (begin2 >= n){begin2 = n;end2 = n - 1;}//end2数组越界else if (end2 >= n){end2 = n - 1;}int i = begin1;while (begin1 <= end1 && begin2 <= end2){// "<"升序if (a[begin1] < a[begin2]){temp[i++] = a[begin1++];}else{temp[i++] = a[begin2++];}}while (begin1 <= end1){temp[i++] = a[begin1++];}while (begin2 <= end2){temp[i++] = a[begin2++];}}//拷贝到原数组中memcpy(a, temp, sizeof(int)*n);//每次每组扩大2倍grap *= 2;}free(temp);
}
8. 计数排序
简介:因为数组下标为整数,因此对于整型数据,我们可以遍历一般然后计数,最后再遍历一般写入。
图示: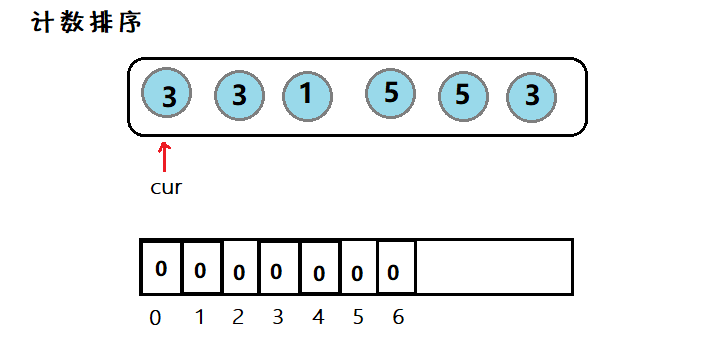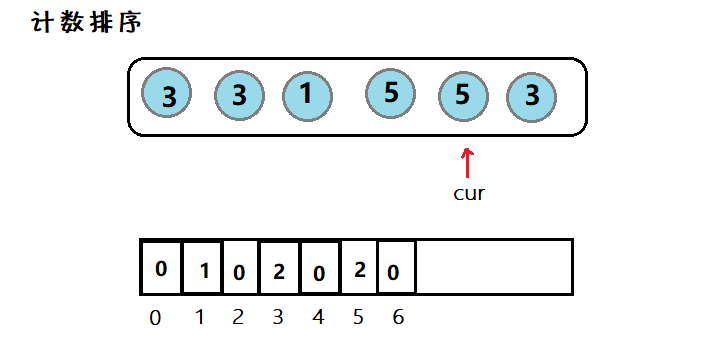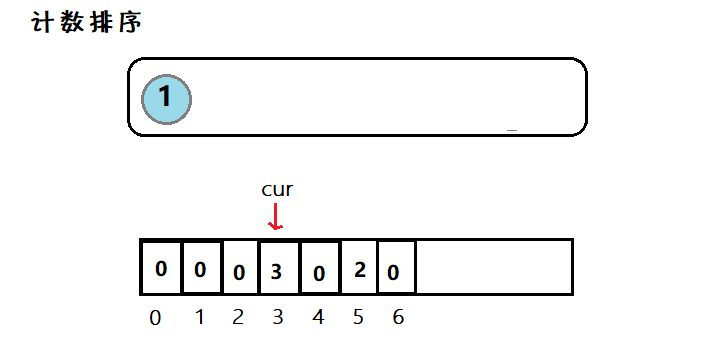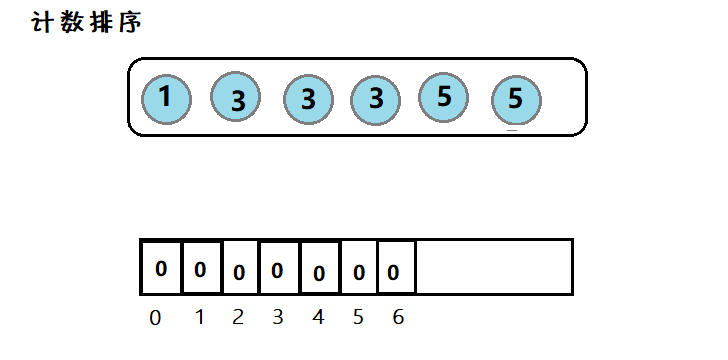
利用数组下标,来在该空间位置存放个数,然后在遍历数组,使之有序。但是适用范围有限。
代码:
// 计数排序
void CountSort(int* a, int n)
{//找到数据中的max与min的数int max = a[0], min = a[0];for (int i = 1; i < n; ++i){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}//这所需开辟数组大小为//所开辟数组[0,range-1]//与原数据中[mini,maxi],构成映射int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));//计数for (int i = 0; i < n; ++i){count[a[i]-min]++;}//进行排序int j = 0;for (int i = 0; i < range; ++i){while (count[i]--){//从映射中还原a[j++] = i + min;}}free(count);
}
效率:时间复杂度为O(N)O(N)O(N)
三、总结
稳定性:对于原数据中,相同值、不同先后顺序的元素,进行排序后,如果其先后顺序任未改变,则称该排序算法是稳定的。
通常稳定主要用于对一组原始数据(每个元素有多个属性值),按照不同规律进行排序时才非常重要。
1. 分析
下面👇同种算法,时间复杂度最好或最坏的情况,其代码可能不同(有无优化)
| 排序算法 | 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O(n2)O(n^2)O(n2) | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 希尔排序 | O(n1.3)O(n^{1.3})O(n1.3) | O(n1.3)O(n^{1.3})O(n1.3) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 不稳定 |
| 选择排序 | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 不稳定 |
| 堆排序 | O(nlog2n)O(nlog_2n)O(nlog2n) | O(nlog2n)O(nlog_2n)O(nlog2n) | O(nlog2n)O(nlog_2n)O(nlog2n) | O(1)O(1)O(1) | 不稳定 |
| 冒泡排序 | O(n2)O(n^2)O(n2) | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 快速排序 | O(nlog2n)O(nlog_2n)O(nlog2n) | O(nlog2n)O(nlog_2n)O(nlog2n) | O(n2)O(n^2)O(n2) | O(log2n)O(log_2n)O(log2n)~O(n)O(n)O(n) | 不稳定 |
| 归并排序 | O(nlog2n)O(nlog_2n)O(nlog2n) | O(nlog2n)O(nlog_2n)O(nlog2n) | O(nlogn)O(nlog_n)O(nlogn) | O(n)O(n)O(n) | 稳定 |
| 计数排序 | O(n)O(n)O(n) | O(n)O(n)O(n) | O(n)O(n)O(n) | O(max(n,range))O(max(n,range))O(max(n,range)) | 无 |
该总结,还是要结合前面详细的讲解,自己要能够分析出来。
🦀🦀观看~~
相关文章:

(数据结构)八大排序算法
目录一、常见排序算法二、实现1. 直接插入排序2.🌟希尔排序3. 选择排序4.🌟堆排序5. 冒泡排序7. 🌟快速排序7.1 其他版本的快排7.2 优化7.3 ⭐非递归7. 🌟归并排序7.1 ⭐非递归8. 计数排序三、总结1. 分析排序 (Sorting) 是计算机…...
构建GRE隧道打通不同云商的云主机内网
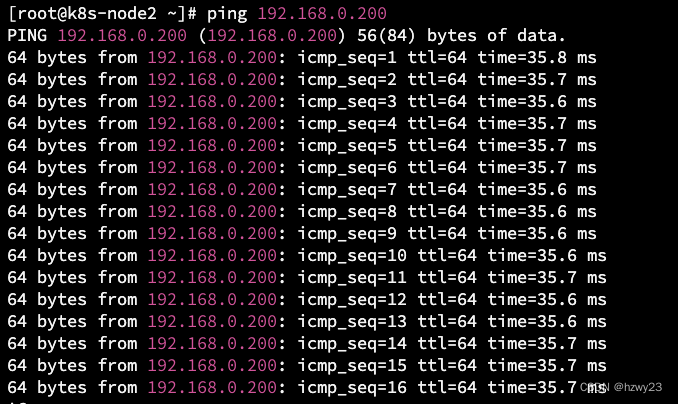
文章目录1. 环境介绍2 GRE隧道搭建2.1 华为云 GRE 隧道安装2.2 阿里云 GRE 隧道安装3. 设置安全组4. 验证GRE隧道4.1 在华为云上 ping 阿里云云主机内网IP4.2 在阿里云上 ping 华为云云主机内网IP5. 总结1. 环境介绍 华为云上有三台云主机,内网 CIDR 是 192.168.0.0…...
48天C++笔试强训 001
作者:小萌新 专栏:笔试强训 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:讲解48天笔试强训第一天的题目 笔试强训 day1选择题12345678910编程题12选择题 1 以下for循环的执行次数是(ÿ…...
Android 11新增系统服务
1.编写.aidl文件存放位置:frameworks/base/core/java/android/ospackage android.os;interface ISystemVoiceServer {void setHeightVoice(int flag);void setBassVoice(int flag);void setReverbVoice(int flag);}2.将.aidl文件添加到frameworks/base/Android.bp f…...

“你要多弄弄算法”
开始瞎掰 ▽ 2月的第一天,猎头Luna给我推荐了字节的机会,菜鸡我呀,还是有自知之明的,赶忙婉拒:能力有限,抱歉抱歉。 根据我为数不多的和猎头交流的经验,一般猎头都会稍微客套一下:…...

【数据结构】千字深入浅出讲解队列(附原码 | 超详解)
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石. 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:C语言实现数据结构 💬总结:希望你看完…...
)
vue面试题(day04)
vue面试题vue插槽?vue3中如何获取refs,dom对象的方式?vue3中生命周期的和vue2中的区别?说说vue中的diff算法?说说 Vue 中 CSS scoped 的原理?vue3中怎么设置全局变量?Vue中给对象添加新属性时&a…...

自动标注工具 Autolabelimg
原理简介~~ 对于数据量较大的数据集,先对其中一部分图片打标签,Autolabelimg利用已标注好的图片进行训练,并利用训练得到的权重对其余数据进行自动标注,然后保存为xml文件。 一、下载yolov5v6.1 https://github.com/ultralytic…...

2023-03-20干活
transformer复现 from torch.utils.data import Dataset,DataLoader import numpy as np import torch import torch.nn as nn import os import time import math from tqdm import tqdmdef get_data(path,numNone):all_text []all_label []with open(path,"r",e…...
)
Java 注解(详细学习笔记)
注解 注解英文为Annotation Annotation是JDK5引入的新的技术 Annotation的作用: 不是程序本身,可以对程序做出解释可以被其他程序(比如编译器)读取。 Annotation的格式: 注解是以注解名在代码中存在的,还…...

LeetCode:35. 搜索插入位置
🍎道阻且长,行则将至。🍓 🌻算法,不如说它是一种思考方式🍀算法专栏: 👉🏻123 一、🌱35. 搜索插入位置 题目描述:给定一个排序数组和一个目标值&…...

菜鸟刷题Day2
菜鸟刷题Day2 一.判定是否为字符重排:字符重排 描述 给定两个由小写字母组成的字符串 s1 和 s2,请编写一个程序,确定其中一个字符串的字符重新排列后,能否变成另一个字符串。 解题思路: 这题思路与昨天最后两道类似&…...

Selenium基础篇之不打开浏览器运行
文章目录前言一、场景二、设计1.引入库2.引入浏览器配置3.设置无头模式4.启动浏览器实例,添加配置信息5.访问质量分地址6.隐式等待5秒7.定位到输入框8.输入博文地址9.定位到查询按钮10.点击查询按钮11.定位到查询结果模块div12.打印结果13.结束webdriver进程三、结果…...

【数据结构初阶】栈与队列笔试题
前言在我们学习了栈和队列之后,今天来通过几道练习题来巩固一下我们的知识。题目一 用栈实现队列题目链接:232. 用栈实现队列 - 力扣(Leetcode)这道题难度不是很大,重要的是我们对结构认识的考察,由于这篇文…...
【Linux入门篇】操作系统安装、网络配置
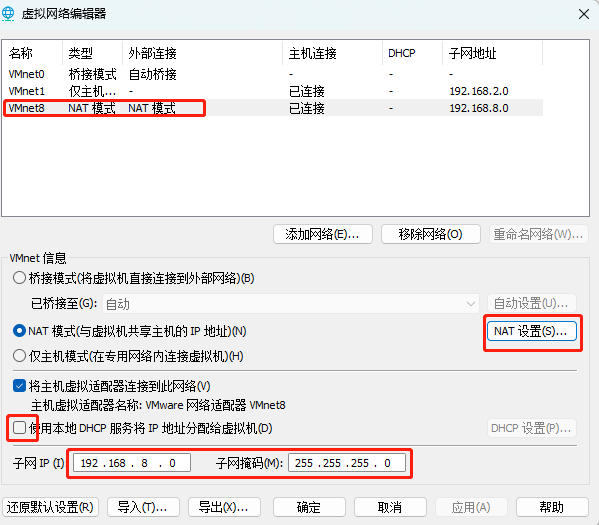
目录 🍁Linux详解 🍂1.操作系统 🍂2.操作系统组成 🍂3.操作系统历史 🍂4.常见的Linux系统 🍂5.centos7下载 🍂6.安装centos7 🍁linux初始化配置 🍃1.虚拟机系统安装后操作…...

Selenium:找不到对应的网页元素?常见的一些坑
目录 1. 用Xpath查找数据时无法直接获取节点属性 2. 使用了WebDriverWait以后仍然无法找到元素 2.1. 分辨率原因 2.2. 需要滚动页面 2.3. 由于其他元素的遮挡 1. 用Xpath查找数据时无法直接获取节点属性 通常在我们使用xpath时,可以使用class的方式直接获取节…...
flex布局优化(两端对齐,从左至右)
文章目录前言方式一 nth-child方式二 gap属性方式三 设置margin左右两边为负值总结前言 flex布局是前端常用的布局方式之一,但在使用过程中,我们总是感觉不太方便,因为日常开发中,大多数时候,我们想要的效果是这样的 …...
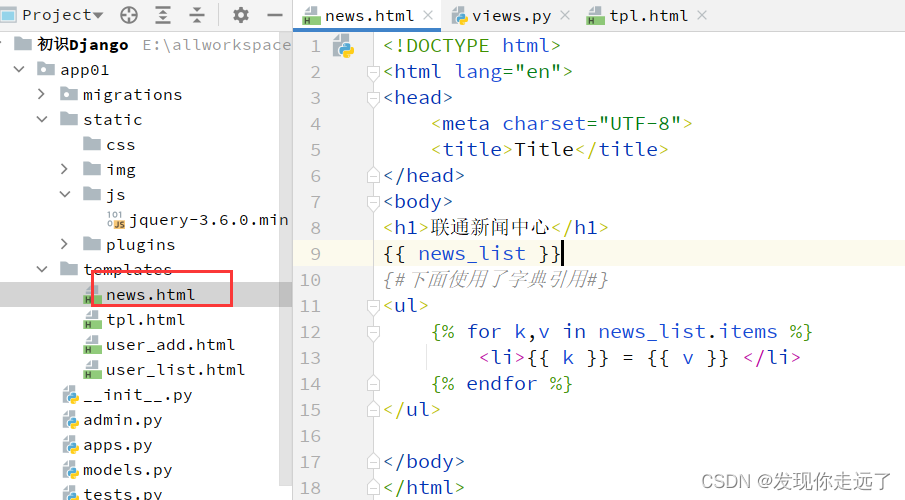
【Django 网页Web开发】03. 初识Django(保姆级图文)
目录1. 命令行创建与pycharm创建的区别2. 项目结构信息2.1 项目结构2.2 项目app结构2.3 快速查看项目结构树3. 创建并注册app3.1 创建app3.2 注册app4. 编写URL与视图的对应关系5. 编写视图文件6. 启动项目7. 写多个页面8. templates模板的使用8.1 编写html文件8.3 导入html文件…...

KubeSphere All in one安装配置手册
KubeSphere All in one安装配置手册 1. 初始化 1.1 配置apt源 # vi /etc/apt/sources.list deb https://mirrors.aliyun.com/ubuntu/ focal main restricted universe multiverse deb-src https://mirrors.aliyun.com/ubuntu/ focal main restricted universe multiversedeb…...

Spring Boot 核心配置文件
Spring Boot 核心配置文件1、application.properties2、application.yml使用建议3、常用配置项服务器配置数据库配置日志配置其他配置4、配置文件的加载顺序5、配置文件的占位符6、配置文件的动态刷新7、配置文件的属性分组定义属性分组绑定属性分组使用属性分组总结Spring Boo…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
