手撕数据结构—栈
Tips
不得不再次提一下这个语法问题,当数组创建的时候,进行初始化的时候,分为全部初始化或者说部分初始化,对于不完全初始化而言,剩下的部分就全部默认为零。现在比如说你想对整型数组的1万个元素把它全部变成-1,不能够仅仅在一个花括号里面写个-1,只是第一个元素变成-1,然后其他的都变成0了。之后你只能用memset
栈以及先进后出原则
栈和队列其实也是一个线性表。线性表也就是说你这个数据至少在逻辑上都是依次线性存储,一个一个挨着挨着这样存储这么一个概念。
栈作为一种特殊的线性表,它只允许在固定的一端进行数据的插入或删除元素操作。进行数据插入和删除操作的那一端就被称为栈顶。因此很容易理解栈中的数据元素遵守后进先出原则。
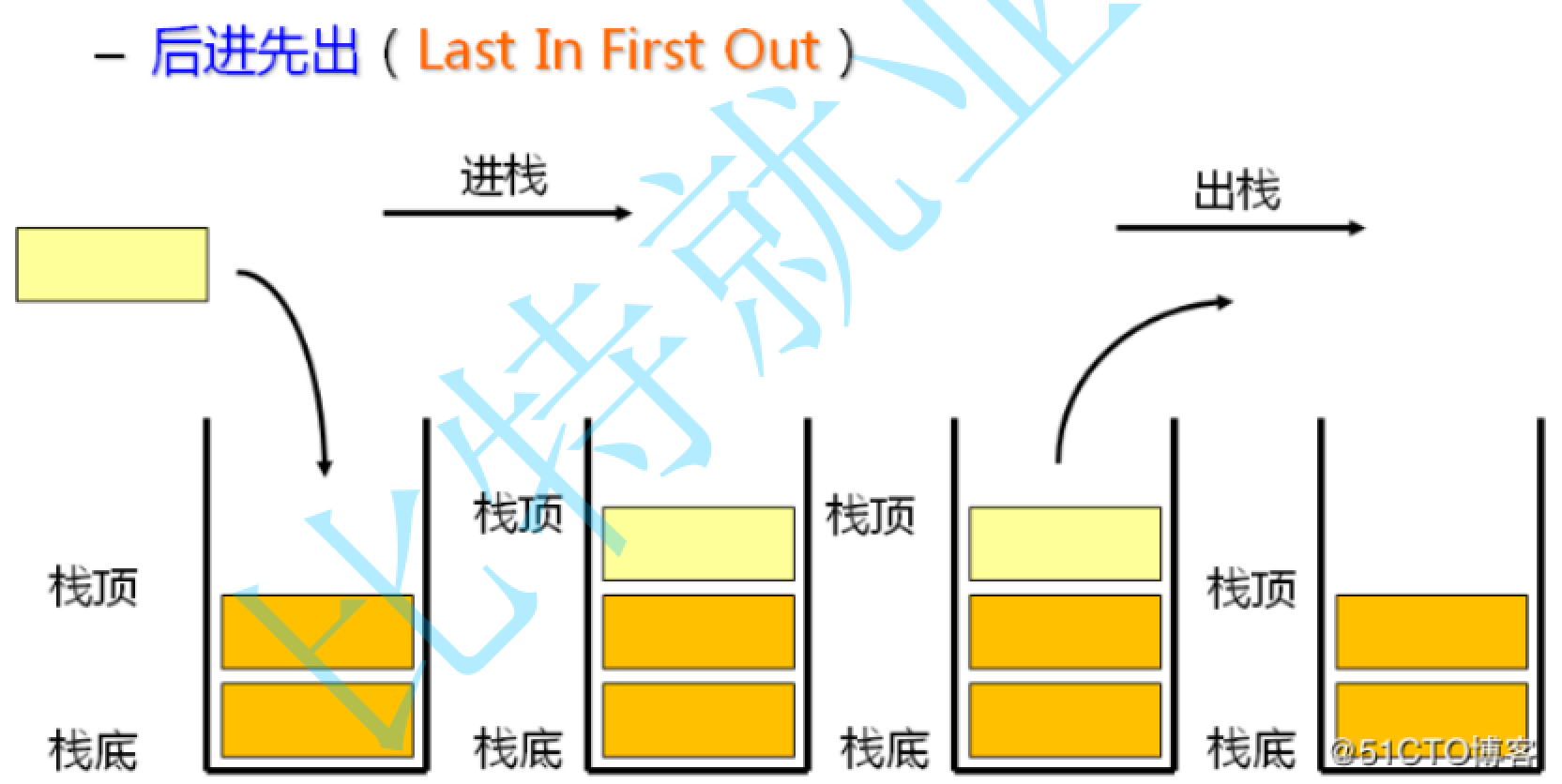
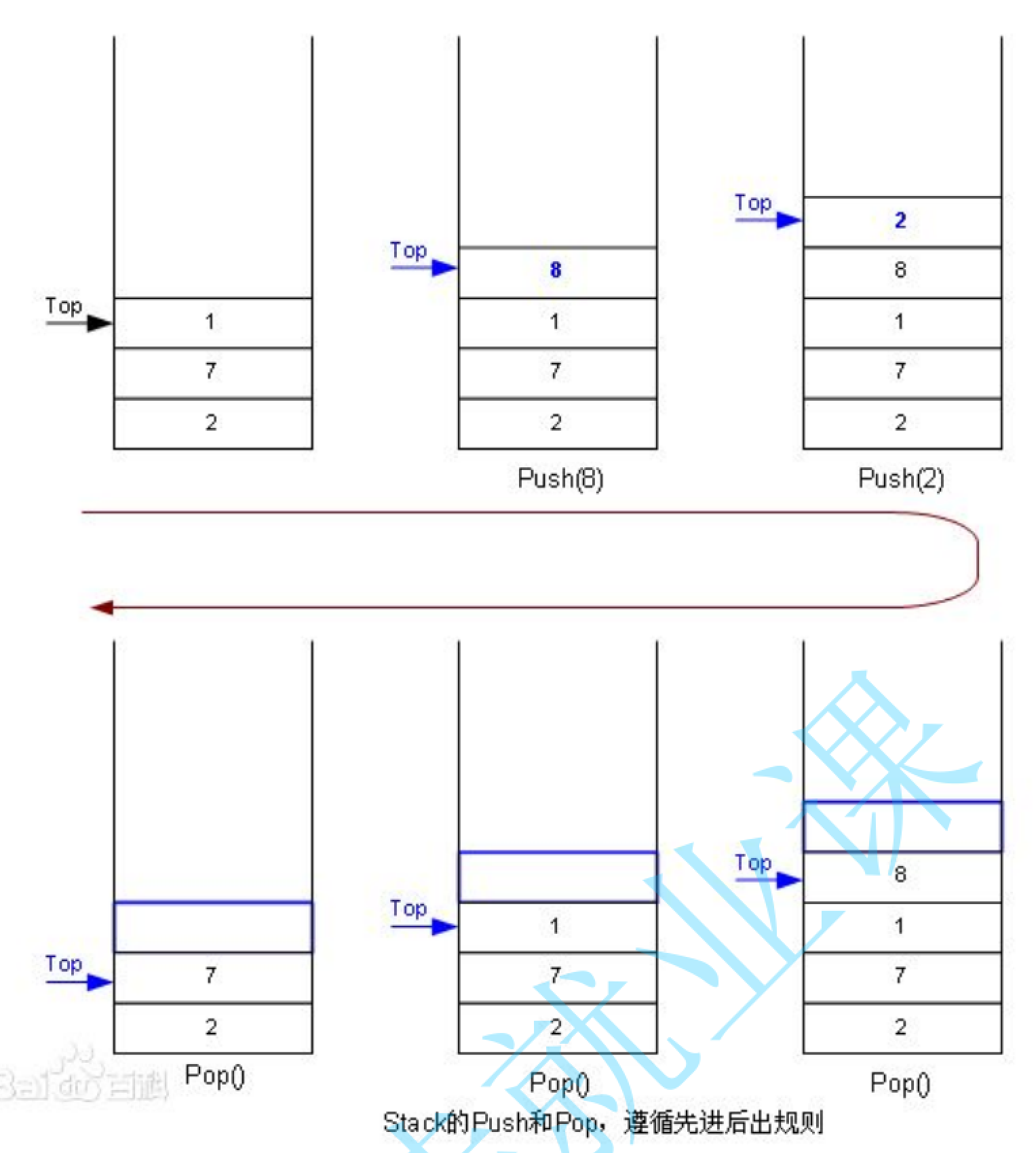
压栈与出栈
栈的插入操作叫做进栈/压栈/入栈,这是在栈顶完成的。
栈的删除操作叫做出栈,这也是在栈顶完成的。所以说它是在同一端进行操作。
在这边值得一提的是,比如说现在有一堆元素,对于同一进栈的顺序,但是出栈序列可以多种多样,因为并没有规定什么时候可以出栈,你可以使所有元素放进栈里面之后再依次出栈;当然你也可以是在边进栈的过程中可以出栈。我随便举个例子好了:比如说进栈序列为1234,那么出栈序列可以比如为1432,2341,3421,但是断然断然不可能是3124。
栈的实现
栈的话可以用数组去实现,也可以用链表去实现。肯定是数组,用数组来实现栈的话嘎嘎香啊,比如说你就可以把数组的右端当成一个栈的栈顶。如果要说真有一个弊端的话,那就是说用数组来模拟栈的话需要扩容。
那如果非要用链表去实现,也是完全可以的:能用单链表就用单链表,你用双向链表的话,还多一个指针呢,能省一点就是一点。
但是用单链表的话由于尾删啊尾插啊这些操作都需要去从phead开始去往后去遍历去找尾(注意链表不支持下标访问操作),这会相当的麻烦,因此就想了一个办法。把整个链表的左端当成栈顶,那么这样子的话,我的入栈与出栈相当于单链表的头插头删,效率非常之高。
但如果说非要选一个的话,用数组和链表来模拟的话都非常可以,因为都是O(1)的插入删除(数组的话可以支持下标访问,把数组的右端当成栈顶;链表的话把他的左端当成栈顶,头插头删也是O(1))。可能你还是会选择链表,但是别忘了数组的缓存命中率与利用率比链表要高。
栈的创建(创建结构体)
凡是有多个数据,都放到一个结构体里面。
对于这个结构体有三个要素,一个是容量,一个是栈顶top,还有一个我是等会儿从堆区开辟内存空间之后返回来的地址,需要用一个指针接收一下,标记一下地址。
typedef int STDataType;
typedef struct Stack
{STDataType* p;int top;int capacity;
}ST;栈的初始化
在初始化的时候有一个比较容易出错的地方,就是必须得先搞清楚这个top到底是什么东西,我就假定这个top指向此时此刻的栈顶元素。那么这时候由于要初始化,此时栈顶也压根儿没有任何元素,因此top就指向-1/那如果我说这个top是栈顶元素的下一个位置,那此时此刻初始化的时候,这个top应该指向0。
我们为了跟之前的顺序表保保持一致,初始化的时候,这个top就给他弄成0。此时此刻,你只需要记住top的一个含义:他现在就表示栈中的元素个数
#define INIT_CAPACITY 5
void STInit(ST* ps)
{assert(ps);ps->p = (STDataType*)malloc(sizeof(STDataType) * INIT_CAPACITY);if (ps->p == NULL){perror("STInit::Malloc");return;}ps->top = 0;ps->capacity = INIT_CAPACITY;
}栈的销毁
void STDestroy(ST* ps)
{assert(ps);free(ps->p);ps->p = NULL;ps->top = 0;ps->capacity = 0;
}入栈
void STPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity){STDataType* pp = (STDataType*)realloc(ps->p, sizeof(STDataType) * (ps->capacity) * 2);if (pp == NULL){perror("STPush::Realloc");return;}ps->p = pp;ps->capacity *= 2;}ps->p[ps->top] = x;ps->top++;
}栈的判断是否为空
bool STEmpty(ST* ps)
{assert(ps);return ps->top==0;
}栈的求元素个数
int STSize(ST* ps)
{assert(ps);return ps->top;
}出栈
void STPop(ST* ps)
{assert(ps);assert(!STEmpty(ps));ps->top--;
}栈的求栈顶元素
int STTop(ST* ps)
{assert(ps);assert(!STEmpty(ps));return ps->p[ps->top - 1];
}注:
虽然从代码上看起来与顺序表非常非常的相像。但是栈的话一定要记住他的特性,那就是后进先出。比如说:23458,我如果要访问5,那么8就必须先出去,如果说我要访问3,那么458就必须先出去。正是因为这种后进先出的特性,这也导致了我们没有写打印栈这种函数,因为栈这种玩意儿,他是不支持去遍历的,这是规定死的。
这些都是由栈的性质决定的,否则他就不叫做栈了。对于先进栈的数据,想要对他进行任何的操作,包括访问与打印,都必须把它之前栈顶的元素全部弹出去才可以,不然永远只能对栈顶的那个元素动手。
相关文章:

手撕数据结构—栈
Tips不得不再次提一下这个语法问题,当数组创建的时候,进行初始化的时候,分为全部初始化或者说部分初始化,对于不完全初始化而言,剩下的部分就全部默认为零。现在比如说你想对整型数组的1万个元素把它全部变成-1&#x…...

【java刷题】排序子序列
这里写目录标题问题描述解决思路实现代码问题描述 牛牛定义排序子序列为一个数组中一段连续的子序列,并且这段子序列是非递增或者非递减排序的。牛牛有一个长度为n的整数数组A,他现在有一个任务是把数组A分为若干段排序子序列,牛牛想知道他最少可以把这个数组分为几段排序子序…...
Springboot怎么快速集成Mybatis和thymeleaf?
前言有时候做方案,需要模拟一些业务上的一些场景来验证方案的可行性,基本上每次都是到处百度如何集成springbootmybatisthymeleaf这些东西的集成平时基本上一年也用不了一次,虽然比较简单,奈何我真得记不住详细的每一步࿰…...

shell常见面试题一
(1)、set //查看系统变量 (2)、chsh -s /bin/zsh test //修改用户登录shell (3)、2>&1 //标准错误重定向到标准输出 &> //同样可以将标准错误重定向到标准输出 如下: ls test.…...

python如何快速采集美~女视频?无反爬
人生苦短 我用python~ 这次康康能给大家整点好看的不~ 环境使用: Python 3.8 Pycharm mou歌浏览器 mou歌驱动 —> 驱动版本要和浏览器版本最相近 <大版本一样, 小版本最相近> 模块使用: requests >>> pip install requests selenium >>> pip …...
kali内置超好用的代理工具proxychains
作者:Eason_LYC 悲观者预言失败,十言九中。 乐观者创造奇迹,一次即可。 一个人的价值,在于他所拥有的。所以可以不学无术,但不能一无所有! 技术领域:WEB安全、网络攻防 关注WEB安全、网络攻防。…...

Java栈和队列·下
Java栈和队列下2. 队列(Queue)2.1 概念2.2 实现2.3 相似方法的区别2.4 循环队列3. 双端队列 (Deque)3.1 概念4.java中的栈和队列5. 栈和队列面试题大家好,我是晓星航。今天为大家带来的是 Java栈和队列下 的讲解!😀 继上一个讲完的栈后&…...
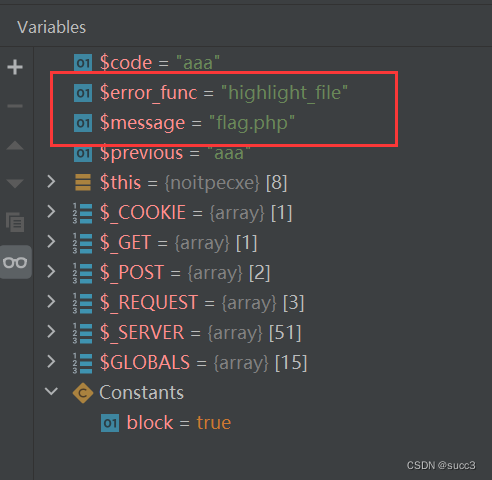
b01lers CTF web 复现
warmup 按照提示依次 base64 加密后访问,可以访问 ./flag.txt,也就是 Li9mbGFnLnR4dA 。 from base64 import b64decode import flaskapp flask.Flask(__name__)app.route(/<name>) def index2(name):name b64decode(name)if (validate(name))…...

三月份跳槽了,历经字节测开岗4轮面试,不出意外,被刷了...
大多数情况下,测试员的个人技能成长速度,远远大于公司规模或业务的成长速度。所以,跳槽成为了这个行业里最常见的一个词汇。 前几天,我看到有朋友留言说,他在面试字节的测试开发工程师的时候,灵魂拷问三小…...
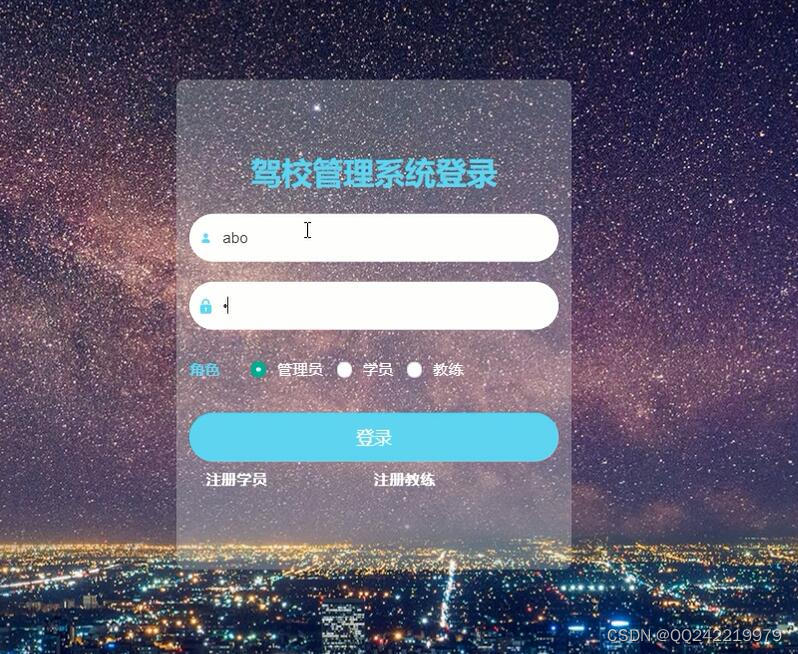
springboot+vue驾校管理系统 idea科目一四预约考试,练车
加大了对从事道路运输经营活动驾驶员的培训管理力度,但在实际的管理过程中,仍然存在以下问题:(1)管理部门内部人员在实际管理过程中存在人情管理,不进行培训、考试直接进行发证。(2)从业驾驶员培训机构不能严格执行管理部门的大纲…...
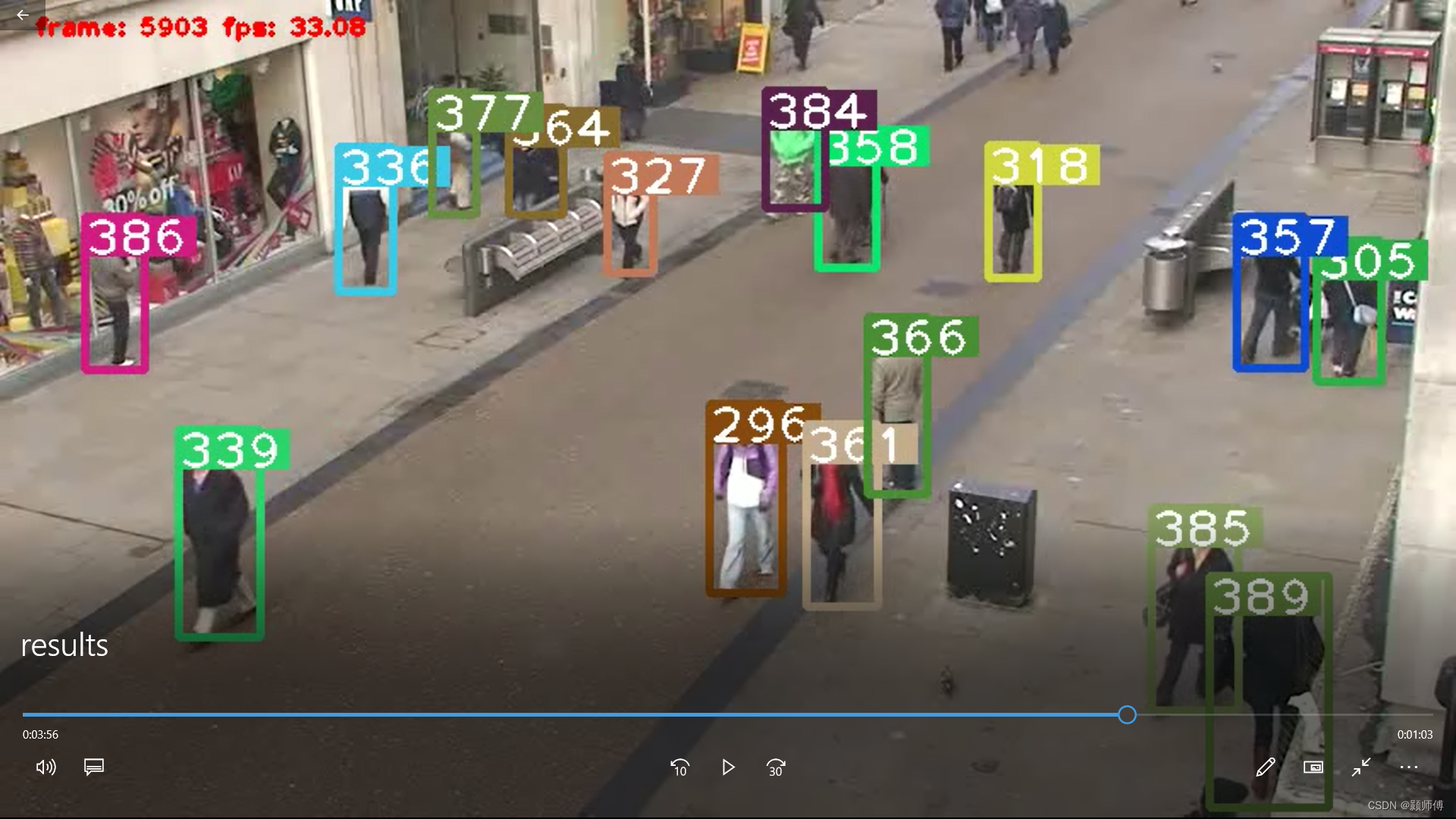
【pytorch】使用deepsort算法进行目标跟踪,原理+pytorch实现
目录deepsort流程一、匈牙利算法二、卡尔曼滤波车速预测例子动态模型的概念卡尔曼滤波在deepsort中的动态模型三、预测值及测量值的含义deepsort在pytorch中的运行deepsort流程 DeepSORT是一种常用的目标跟踪算法,它结合了深度学习和传统的目标跟踪方法。DeepSORT的…...

Python 基础教程【3】:字符串、列表、元组
本文已收录于专栏🌻《Python 基础》文章目录🌕1、字符串🥝1.1 字符串基本操作🍊1.1.1 字符串创建🍊1.1.2 字符串元素读取🍊1.1.3 字符串分片🍊1.1.4 连接和重复🍊1.1.5 关系运算&…...
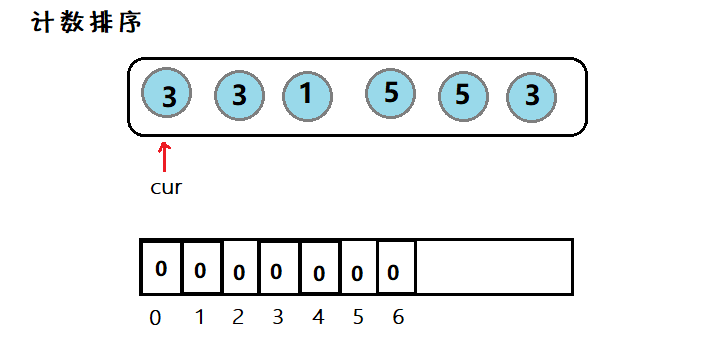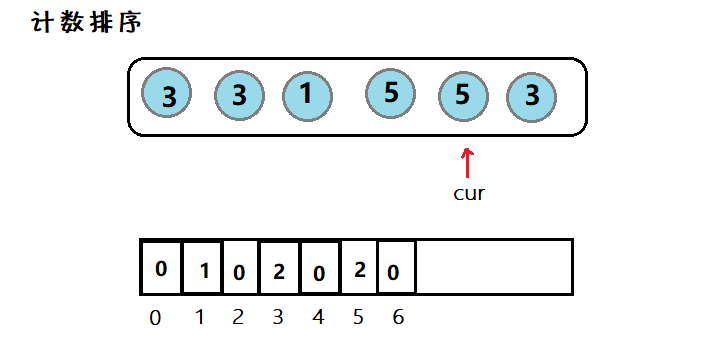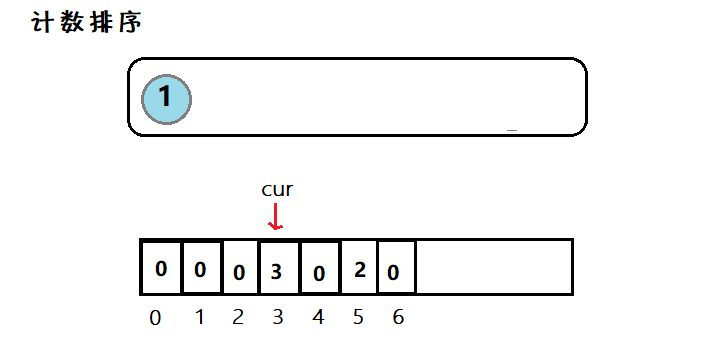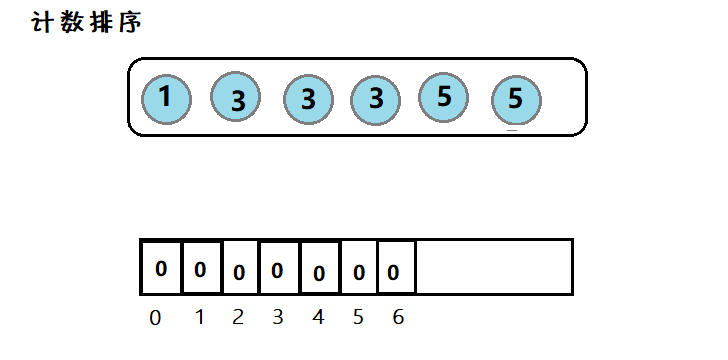
(数据结构)八大排序算法
目录一、常见排序算法二、实现1. 直接插入排序2.🌟希尔排序3. 选择排序4.🌟堆排序5. 冒泡排序7. 🌟快速排序7.1 其他版本的快排7.2 优化7.3 ⭐非递归7. 🌟归并排序7.1 ⭐非递归8. 计数排序三、总结1. 分析排序 (Sorting) 是计算机…...
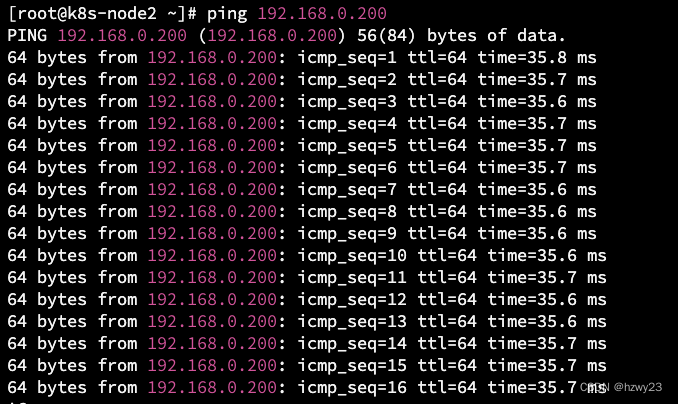
构建GRE隧道打通不同云商的云主机内网
文章目录1. 环境介绍2 GRE隧道搭建2.1 华为云 GRE 隧道安装2.2 阿里云 GRE 隧道安装3. 设置安全组4. 验证GRE隧道4.1 在华为云上 ping 阿里云云主机内网IP4.2 在阿里云上 ping 华为云云主机内网IP5. 总结1. 环境介绍 华为云上有三台云主机,内网 CIDR 是 192.168.0.0…...
48天C++笔试强训 001
作者:小萌新 专栏:笔试强训 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:讲解48天笔试强训第一天的题目 笔试强训 day1选择题12345678910编程题12选择题 1 以下for循环的执行次数是(ÿ…...
Android 11新增系统服务
1.编写.aidl文件存放位置:frameworks/base/core/java/android/ospackage android.os;interface ISystemVoiceServer {void setHeightVoice(int flag);void setBassVoice(int flag);void setReverbVoice(int flag);}2.将.aidl文件添加到frameworks/base/Android.bp f…...

“你要多弄弄算法”
开始瞎掰 ▽ 2月的第一天,猎头Luna给我推荐了字节的机会,菜鸡我呀,还是有自知之明的,赶忙婉拒:能力有限,抱歉抱歉。 根据我为数不多的和猎头交流的经验,一般猎头都会稍微客套一下:…...

【数据结构】千字深入浅出讲解队列(附原码 | 超详解)
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石. 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:C语言实现数据结构 💬总结:希望你看完…...
)
vue面试题(day04)
vue面试题vue插槽?vue3中如何获取refs,dom对象的方式?vue3中生命周期的和vue2中的区别?说说vue中的diff算法?说说 Vue 中 CSS scoped 的原理?vue3中怎么设置全局变量?Vue中给对象添加新属性时&a…...

自动标注工具 Autolabelimg
原理简介~~ 对于数据量较大的数据集,先对其中一部分图片打标签,Autolabelimg利用已标注好的图片进行训练,并利用训练得到的权重对其余数据进行自动标注,然后保存为xml文件。 一、下载yolov5v6.1 https://github.com/ultralytic…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
