CSDN 第三十七期竞赛题解
很少有时间来玩玩题目,上一次因为环境极为嘈杂的原因在时间上没有进入前十,挺遗憾的。
在 CSDN 参加的第一次没出锅的比赛。
大概只有最后一题值得好好讲讲。
T1:幼稚班作业
幼稚园终于又有新的作业了。 老师安排同学用发给同学的4根木棒拼接成一个三角形。 当然按照正常的逻辑,如果不能拼接成三角形。 必然要折断某个木棍来拼接三角形。 可是懒惰的小艺当然不会费力了! 如果拼接不成三角形,小艺就会把它拼接成类似边长 1 1 2的伪三角形(两边之和等于第3边)。 如果伪三角形都拼接不成那就不交作业!
分析
排序 + 三角形判断,注意四根木棍不需要全用。
#include<bits/stdc++.h>
int a[5];
using namespace std;
int main(){scanf("%d%d%d%d",a+1,a+2,a+3,a+4);sort(a+1,a+5);if(a[1]+a[2]>a[3]||a[2]+a[3]>a[4]) return puts("1"),0;else if(a[1]+a[2]==a[3]||a[2]+a[3]==a[4]) return puts("0"),0;puts("-1");
}
T2:异或和
小张找到了一个整数 N,他想问问你从 1 到 N 的所有不同整数的异或和是多少, 请你回答他的问题。(1≤N≤1051\leq N\leq 10^51≤N≤105)
分析
本来以为需要奇偶数分类,没想到是个模拟。
题目限制变成 1≤N≤101051\leq N \leq 10^{10^5}1≤N≤10105 应该更好。
#include<bits/stdc++.h>
int n,ans;
using namespace std;int main(){scanf("%d",&n);for(int i=1;i<=n;i++) ans^=i;printf("%d",ans);
}
T3:大整数替换数位
以字符串的形式给你一个长度为 MMM 的整数 NNN,请你计算出对这个数进行一次操作后模 999 的值为 111 的所有可能的不同操作方式。
在一次操作中, 我们可以选择 NNN 的一个数位 NiN_iNi,并把它替换成另一个不同的 000 到 999 范围之内的数 BBB,当且仅当它们选择的 iii 或 BBB 不同时两种操作方式不同。
分析
首先知道 999 的倍数其满足数位和仍为 999 的倍数。
那么问题变成
求对于一个由 nnn 个一位数组成的序列 NNN,试求改变一个 NiN_iNi,使得 ∑1≤i≤nNi\sum\limits_{1\leq i\leq n}N_i1≤i≤n∑Ni为 999 的倍数的方案数。
因为只能改一位,那么根据原本序列 NNN 的和模 999 的余数,逐位判断并累加答案即可。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int m,a[N],nw,ans;
int main(){scanf("%d",&m);for(int i=1;i<=m;i++) scanf("%1d",a+i),nw+=a[i];nw%=9;nw=(nw+8)%9;for(int i=1;i<=m;i++){if(!nw){if(a[i]==0) ans++;}else{if(a[i]+(9-nw)<10) ans++;if(a[i]-nw>-1) ans++;}}return 0;
}
T4:莫名其妙的键盘
有一个神奇的键盘,你可以用它输入a到z的字符,然而每当你输入一个元音字母(a,e,i,o,u其中之一)的时候,已输入的字
符串会发生一次反转! 比方说,当前输入了tw,此时再输入一个o,此时屏幕上的字符串two会反转成owt。 现给出一个
字符串,若用该键盘输入,有多少种方法可以得到?
分析
注意到“有多少种方法可以得到”实现起来相对麻烦,考虑将问题翻转一下变成将一个字符串不断从左右删除直到长度为 0 的方案数。我们知道一个序列被反转了偶数次后形态不变,而这里从左边删除代表了当前序列已被翻转了奇数次。
于是考虑使用区间 dp 解决。
设 dpi,j,0/1dp_{i,j,0/1}dpi,j,0/1 表示当前删除到区间为 [i,j][i,j][i,j] 并且上一次删除了最左 / 右边字符的方案数。
由区间 [i,j][i,j][i,j] 向 [i+1,j][i+1,j][i+1,j]、[i,j−1][i,j-1][i,j−1] 转移,分四种情况:
- sis_isi 为元音:翻转一次,即 fi+1,j,1=fi+1,j,1+fi,j,0f_{i+1,j,1}=f_{i+1,j,1}+f_{i,j,0}fi+1,j,1=fi+1,j,1+fi,j,0
- sis_isi 为辅音:不用翻转,即 fi+1,j,0=fi+1,j,0+fi,j.0f_{i+1,j,0}=f_{i+1,j,0}+f_{i,j.0}fi+1,j,0=fi+1,j,0+fi,j.0
- sjs_jsj 为元音:翻转一次,即 fi,j−1,0=fi,j−1,0+fi,j,1f_{i,j-1,0}=f_{i,j-1,0}+f_{i,j,1}fi,j−1,0=fi,j−1,0+fi,j,1
- sis_isi 为辅音:不用翻转,即 fi+1,j,1=fi+1,j,1+fi,j,1f_{i+1,j,1}=f_{i+1,j,1}+f_{i,j,1}fi+1,j,1=fi+1,j,1+fi,j,1
那么很明显答案 AnsAnsAns 为
Ans=∑i=1n(fi,j,0+fi,j,1)Ans=\sum\limits_{i=1}^{n}(f_{i,j,0}+f_{i,j,1})Ans=i=1∑n(fi,j,0+fi,j,1)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
char s[205];
LL ans,dp[205][205][2];
bool ck(char ch){if(ch=='a'||ch=='u'||ch=='o'||ch=='e'||ch=='i') return 1;return 0;
}
int main(){scanf("%s",s+1);int ls=strlen(s+1);dp[1][ls][1]=1;for(int l=ls;l;l--){for(int i=1;i+l-1<=ls;i++){int j=i+l-1,cki=ck(s[i]),ckj=ck(s[j]);if(cki) dp[i+1][j][0]+=dp[i][j][1];if(!cki) dp[i+1][j][0]+=dp[i][j][0];if(ckj) dp[i][j-1][1]+=dp[i][j][0];if(!ckj) dp[i][j-1][1]+=dp[i][j][1];}}for(int i=1;i<=ls;i++) ans+=dp[i][i][0]+dp[i][i][1];return 0;
}
感觉最后一题题解敲得超详细,不妨多支持一下?
相关文章:

CSDN 第三十七期竞赛题解
很少有时间来玩玩题目,上一次因为环境极为嘈杂的原因在时间上没有进入前十,挺遗憾的。 在 CSDN 参加的第一次没出锅的比赛。 大概只有最后一题值得好好讲讲。 T1:幼稚班作业 幼稚园终于又有新的作业了。 老师安排同学用发给同学的4根木棒拼接…...

Vue实战【常用的Vue小魔法】
目录🌟前言🌟能让你首次加载更快的路由懒加载,怎么能忘?🌟你是否还记得有一个叫Object.freeze的方法?🌟异步组件那么强,你是不是没用过?🌟你是不是还在comput…...

用C跑爬虫
爬虫自指定的URL地址开始下载网络资源,直到该地址和所有子地址的指定资源都下载完毕为止。 下面开始逐步分析爬虫的实现。 待下载集合与已下载集合 为了保存需要下载的URL,同时防止重复下载,我们需要分别用了两个集合来存放将要下载的URL和…...

【C语言】你真的了解结构体吗
引言✨我们知道C语言中存在着整形(int、short...),字符型(char),浮点型(float、double)等等内置类型,但是有时候,这些内置类型并不能解决我们的需求,因为我们无法用这些单一的内置类型来描述一些复杂的对象,…...

血氧仪是如何得出血氧饱和度值的?
目录 一、血氧饱和度概念 二、血氧饱和度监测意义 三、血氧饱和度的监测方式 四、容积脉搏波计算血氧饱和度原理 五、容积脉搏波波形的测量电路方案 1)光源和光电探测器的集成测量模块:SFH7050—反射式 2)模拟前端 六、市面上血氧仪类型…...
接口和抽象类)
Java全栈知识(3)接口和抽象类
1、抽象类 抽象类就是由abstract修饰的类,其中没有只声明没有实现的方法就是抽象方法,抽象类中可以有0个或者多个抽象方法。 1.1、抽象类的语法 抽象类不能被final修饰 因为抽象类是一种类似于工程中未完成的中间件。需要有子类进行继承完善其功能,所…...
)
JavaScript == === Object.is()
文章目录JavaScript & & Object.is() 相等运算符 全等运算符Object.is() 值比较JavaScript & & Object.is() 相等运算符 相等运算符,会先进行类型转换,将2个操作数转为相同的类型,再比较2个值。 console.log("10&…...
GPT4论文翻译 by GPT4 and Human
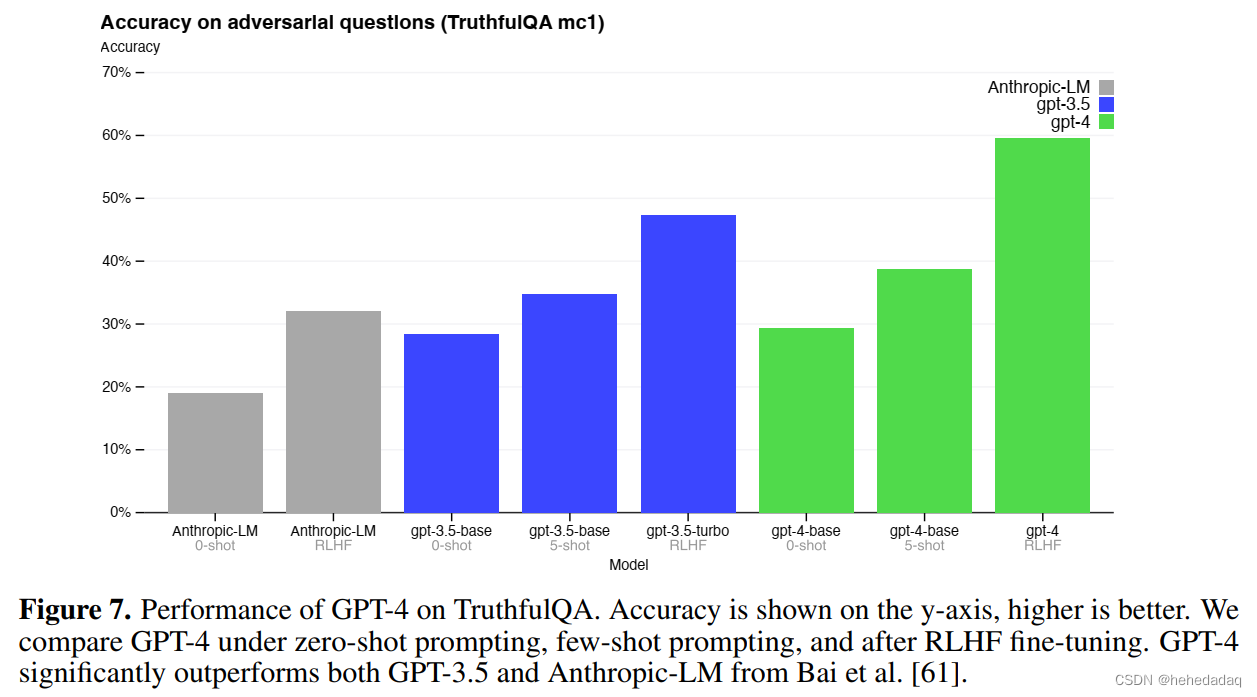
GPT-4技术报告解读 文章目录GPT-4技术报告解读前言:摘要1 引言2 技术报告的范围和局限性3 可预测的扩展性3.1 损失预测3.2 人类评估能力的扩展4 能力评估4.1 视觉输入 !!!5 限制6 风险与缓解:7 结论前言: 这篇报告内容太多了!&am…...
inode和软硬链接
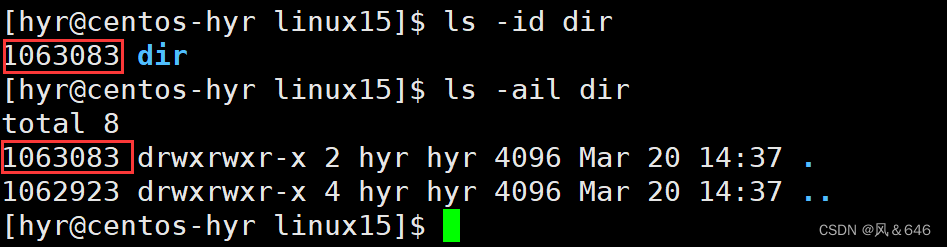
文章目录:一、理解文件系统1.1 什么是inode1.2 磁盘了解1.2.1磁盘的硬件结构1.2.2 磁盘的分区1.2.3 EXT2文件系统二、软硬链接2.1 软链接2.2 硬链接一、理解文件系统 1.1 什么是inode inodes 是文件系统中存储文件元数据的数据结构。每个文件或目录都有一个唯一的 …...

简单分析Linux内核基础篇——initcall
写过Linux驱动的人都知道module_init宏,因为它声明了一个驱动的入口函数。 除了module_init宏,你会发现在Linux内核中有许多的驱动并没有使用module_init宏来声明入口函数,而是看到了许多诸如以下的声明: static int __init qco…...
硬件速攻-AT24CXX存储器
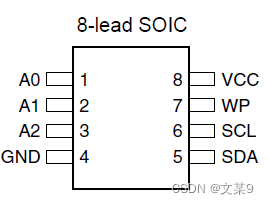
AT24C02是什么? AT24CXX是存储芯片,驱动方式为IIC协议 实物图? 引脚介绍? A0 地址设置角 可连接高电平或低电平 A1 地址设置角 可连接高电平或低电平 A2 地址设置角 可连接高电平或低电平 1010是设备前四位固定地址 …...

C# tuple元组详解
概念 本质就是个数据结构,它是将多个数据元素分组成一个轻型数据结构。 如何声明元组变量(针对.net framework 4.7 和 .net core 2.0) 不带字段名称元组 ## t1就是个变量 它的类型是元组类型 ## 左侧括号定义的是参数列表 等于号右侧就是个t1赋值 #…...
1、Linux初级——linux命令
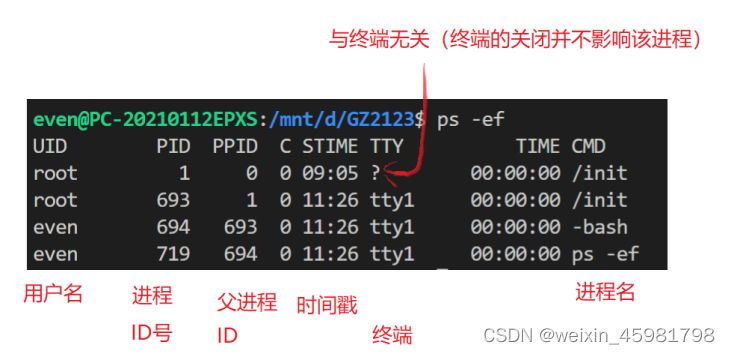
下载镜像:http://cn.ubuntu.com/dowload 一、基本命令 1、alias(给命令取别名) 例如:alias clls -la(只是临时的) 2、配置文件$ vim ~/.bashrc $ vim ~/.bashrc // 使用vim打开配置文件 (1)在配置文件…...
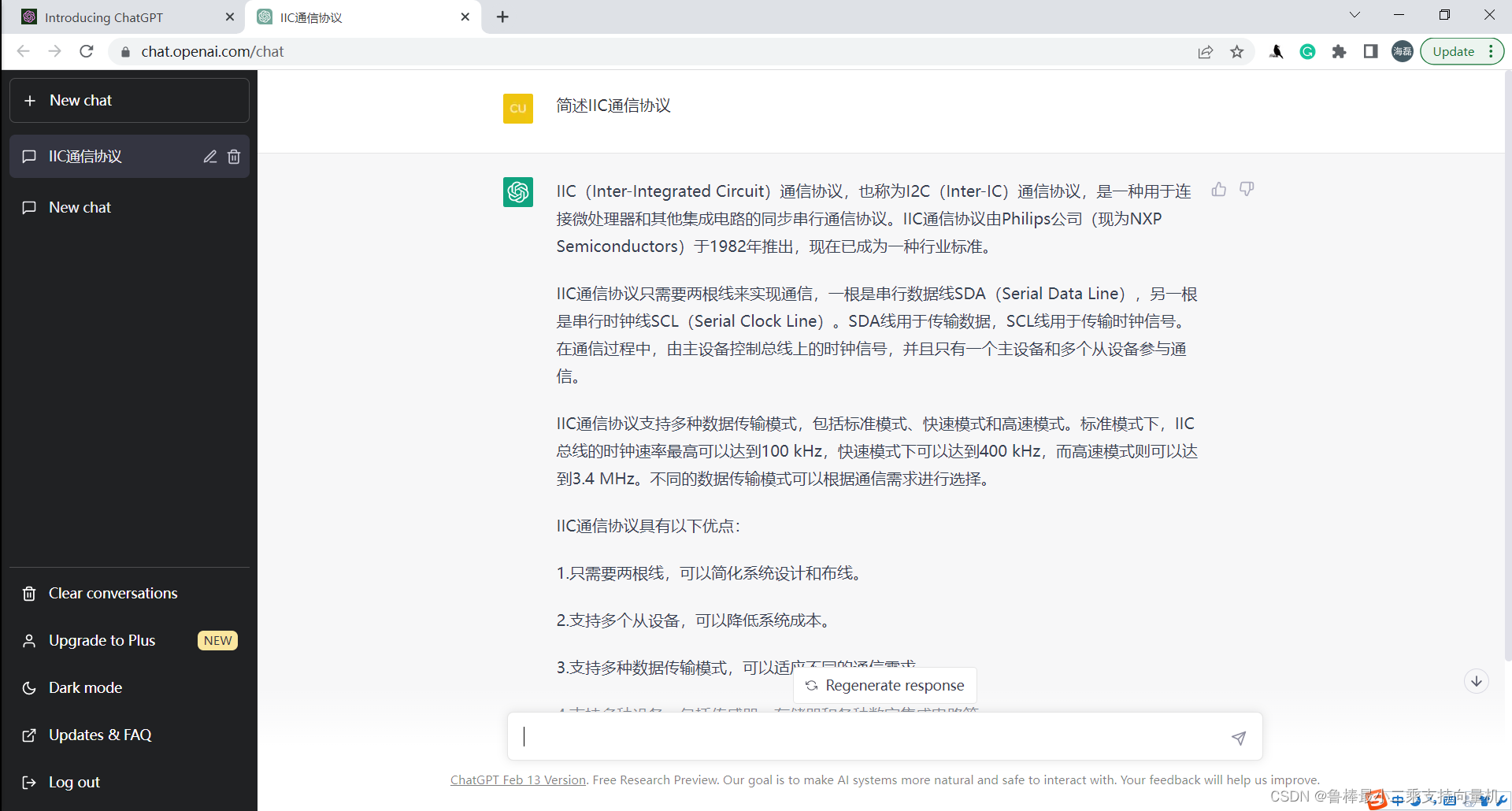
ChatGPT助力校招----面试问题分享(四)
1 ChatGPT每日一题:电阻如何选型 问题:电阻如何选型 ChatGPT:电阻的选型通常需要考虑以下几个方面: 额定功率:电阻的额定功率是指电阻能够承受的最大功率。在选型时,需要根据电路中所需要的功率确定所选…...
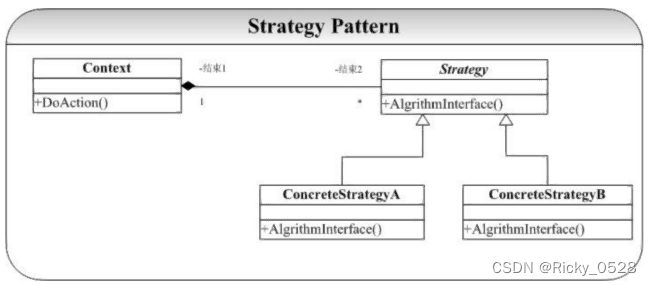
【设计模式】创建型设计模式
文章目录1. 基础①如何学习设计模式② 类模型③ 类关系2. 设计原则3. 模板方法① 定义②背景③ 要点④ 本质⑤ 结构图⑥ 样例代码4. 观察者模式① 定义②背景③ 要点④ 本质⑤ 结构图⑥ 样例代码5. 策略模式① 定义②背景③ 要点④ 本质⑤ 结构图⑥ 样例代码1. 基础 ①如何学习…...

Linux 信号(signal):信号的理解
目录一、理解信号1.信号是什么2.信号的种类二、简单理解信号的生命周期一、理解信号 1.信号是什么 Linux中的信号其实和日常生活中的信号还是挺像的,LInux中的信号是一种事件通知机制,通知进程发生了某个事件。进程接收到信号后,就会中断当前…...
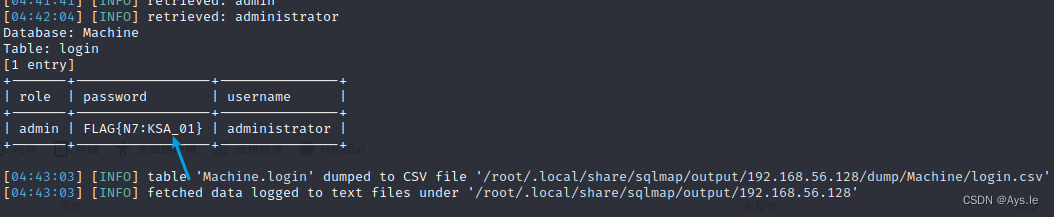
Vulnhub项目:Web Machine(N7)
靶机地址:Web Machine(N7)渗透过程:kali ip:192.168.56.104,靶机ip,使用arp-scan进行查看靶机地址:192.168.56.128收集靶机开放端口:nmap -sS -sV -T5 -A 192.168.56.128开放了80端口࿰…...
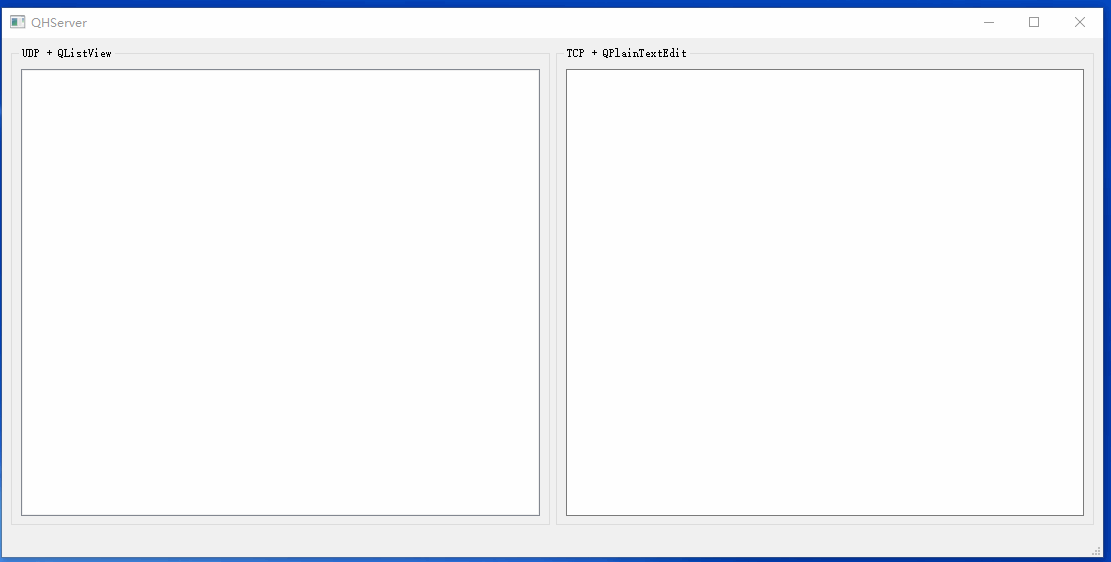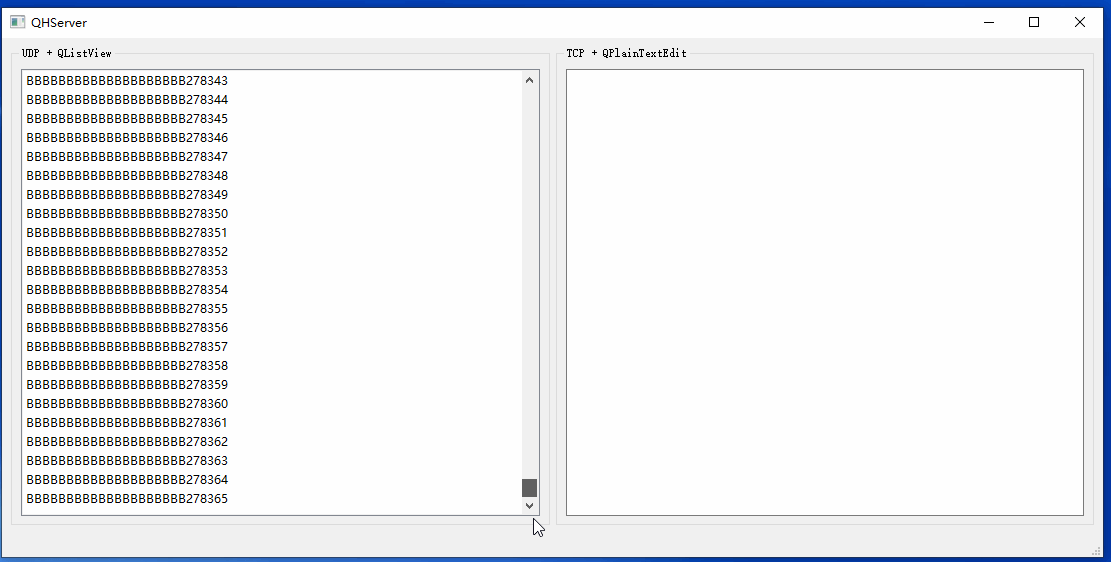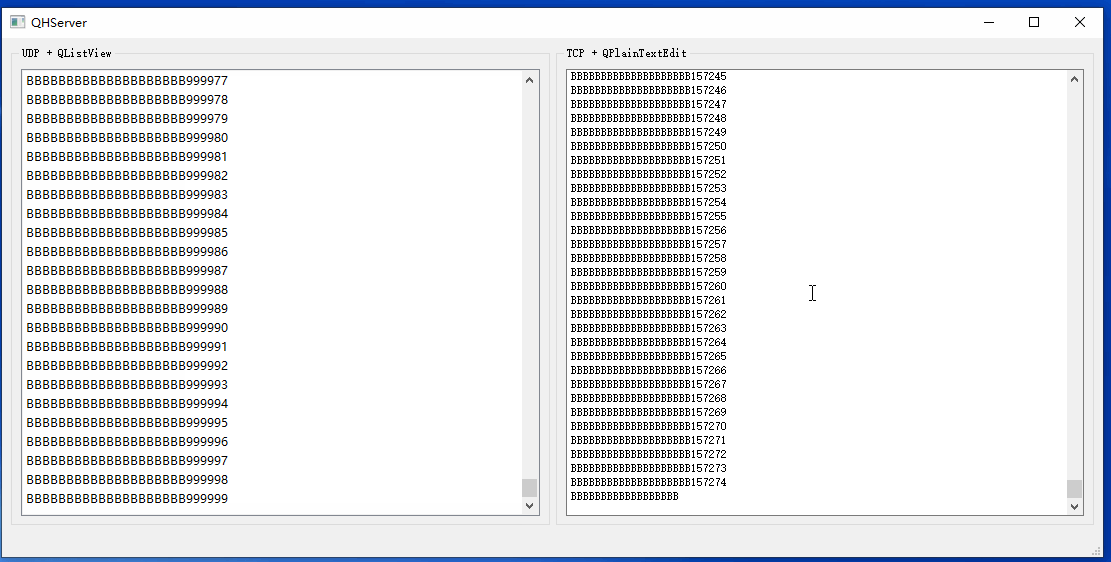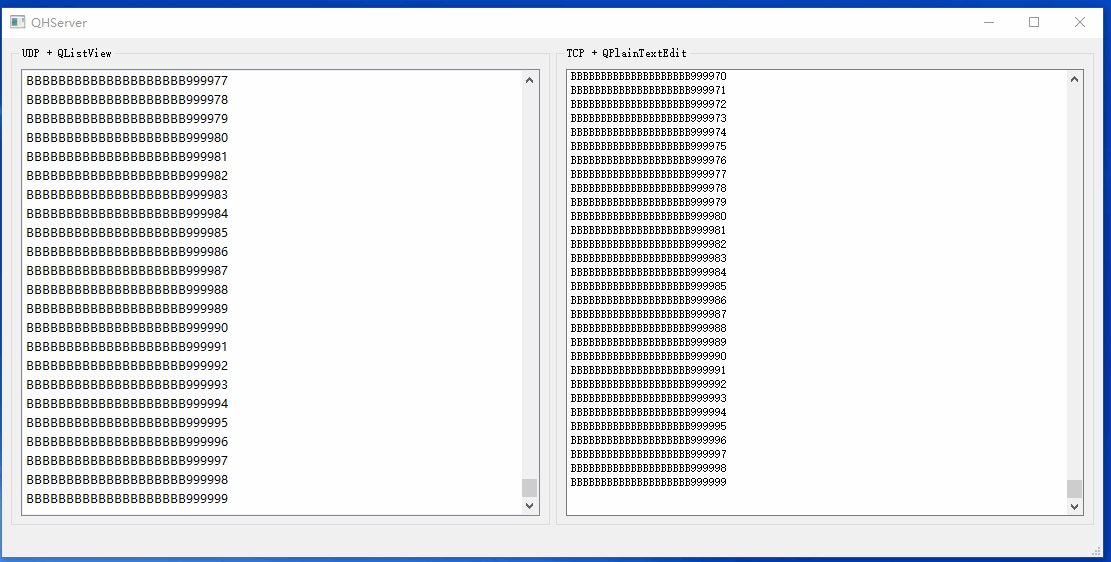
Qt基础之三十三:海量网络数据实时显示
开发中我们可能会遇到接收的网络数据来不及显示的问题。最基础的做法是限制UI中加载的数据行数,这样一来可以防止内存一直涨,二来数据刷新非常快,加载再多也来不及看。此时UI能看到数据当前处理到什么阶段就行,实时性更加重要,要做数据分析的话还得查看日志文件。 这里给出…...

linux console快捷键
Ctrl C:终止当前正在运行的程序。Ctrl D:关闭当前终端会话。Ctrl Z:将当前程序放入后台运行。Ctrl L:清除当前屏幕并重新显示命令提示符。Ctrl R:在历史命令中进行逆向搜索。Ctrl A:将光标移动到行首…...
)
弗洛伊德龟兔赛跑算法(弗洛伊德判圈算法)
弗洛伊德( 罗伯特・弗洛伊德)判圈算法(Floyd Cycle Detection Algorithm),又称龟兔赛跑算法(Tortoise and Hare Algorithm),是一个可以在有限状态机、迭代函数或者链表上判断是否存在环,以及判断环的起点与长度的算法。昨晚刷到一个视频&…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
