机械学习—零基础学习日志(高数22——泰勒公式理解深化)

核心思想:函数逼近
在泰勒的年代,如果想算出e的0.001次方,这是很难计算的。那为了能计算这样的数字,可以尝试逼近的思想。
但是函数又不能所有地方都相等,那退而求其次,只要在一个极小的范围,可以持续逼近就可以了。这里可以看看具体如何逼近呢?
第一步:逼近处的函数值应当一样

可以看到,在重合点处,函数值相同,那这逼近了吗,不对,差距太大了。为什么呢,很明显在重合点之外的地方,差得都太多了。因为趋势不对,那趋势一样呢?
第二步:逼近处的一阶导数一样
那就要求函数值一样,同时导数一样。

这已经非常接近,但是为什么函数值一样,导数值一样,看上去还是不那么贴合呢?因为导数的导数,趋势还不够!斜率不够接近!所以想到了二阶导。
第三步:斜率变化趋势,二阶导一样再试试

第四步:斜率变化趋势的趋势,三阶导一样再试试
......
第五步:斜率变化趋势的趋势的趋势,四阶导一样再试试
......
导数是局部的性质,所以一阶,二阶,三阶,不影响其他部分的趋势。
使用幂函数贴近非常有意义
我们回顾一下一个多项式函数求导的过程~以这个函数为例。

我们算一阶导,二阶导,三阶导.....

当我们代入x=0,以及在多重导的情况下,存在两种情况,第一,常数项被导没,第二,存在有x的项数代入x= 0,也没了。
在这种情况下,具体的三阶导,只和其系数有关。


所以,其实n阶导数,在x= 0时,导数只和n次项数前的系数,以及n的阶乘有关。
再回过来看e的x次方
一个函数f(x),作为多项式,假设是f(x) = a + bx + cx² + dx³....,那其实常数项由a决定,b决定一阶导,c决定二阶导。。。
那如果e的x次方,使用多项式逼近,也就是上述的f(x) = a + bx + cx² + dx³....

我们知道,e的x次方,导数都是e的x次方,又在x = 0处求导,所以导数都是1。那我们就可以确定对应的a , b , c 等等所有值了。

皮亚诺公式:

进一步思考,那如果x不再趋近于0,而是趋近于1,例如,f(1)的三次方,还可以使用上面的规律吗?
是可以的,我们只需要把式子改成( x )改写成 ( x - 1 ) 就可以。
因为在构造对应的式子时,我们巧妙利用了,高阶导去除常数项,以及x = x0为零的特点,构造了对应多项式。
那我们只需要满足,在对应的点处,f(x)的n阶导数相同,那就其实可以满足对应的基本逻辑。

成立条件:只在x0时成立

这里有很重要的一句话:泰勒展开是更高阶的等价,而之前的x~sinx,只是一阶导的等价
奇思妙想:
我把f(1),直接等价到了e乘以f(0),这种做法是不对的。因为趋近的模式均不再成立,例如f(1)并不等于e*趋近式。
重点参考up主:考研数学王昊元《【数一147】泰勒公式的顶级理解》,他讲得真的不错。
相关文章:

机械学习—零基础学习日志(高数22——泰勒公式理解深化)
核心思想:函数逼近 在泰勒的年代,如果想算出e的0.001次方,这是很难计算的。那为了能计算这样的数字,可以尝试逼近的思想。 但是函数又不能所有地方都相等,那退而求其次,只要在一个极小的范围,…...

Java | Leetcode Java题解之第318题最大单词长度乘积
题目: 题解: class Solution {public int maxProduct(String[] words) {Map<Integer, Integer> map new HashMap<Integer, Integer>();int length words.length;for (int i 0; i < length; i) {int mask 0;String word words[i];in…...

科普文:JUC系列之多线程门闩同步器Condition的使用和源码解读
一、概述 条件锁就是指在获取锁之后发现当前业务场景自己无法处理,而需要等待某个条件的出现才可以继续处理时使用的一种锁。 比如,在阻塞队列中,当队列中没有元素的时候是无法弹出一个元素的,这时候就需要阻塞在条件notEmpty上…...
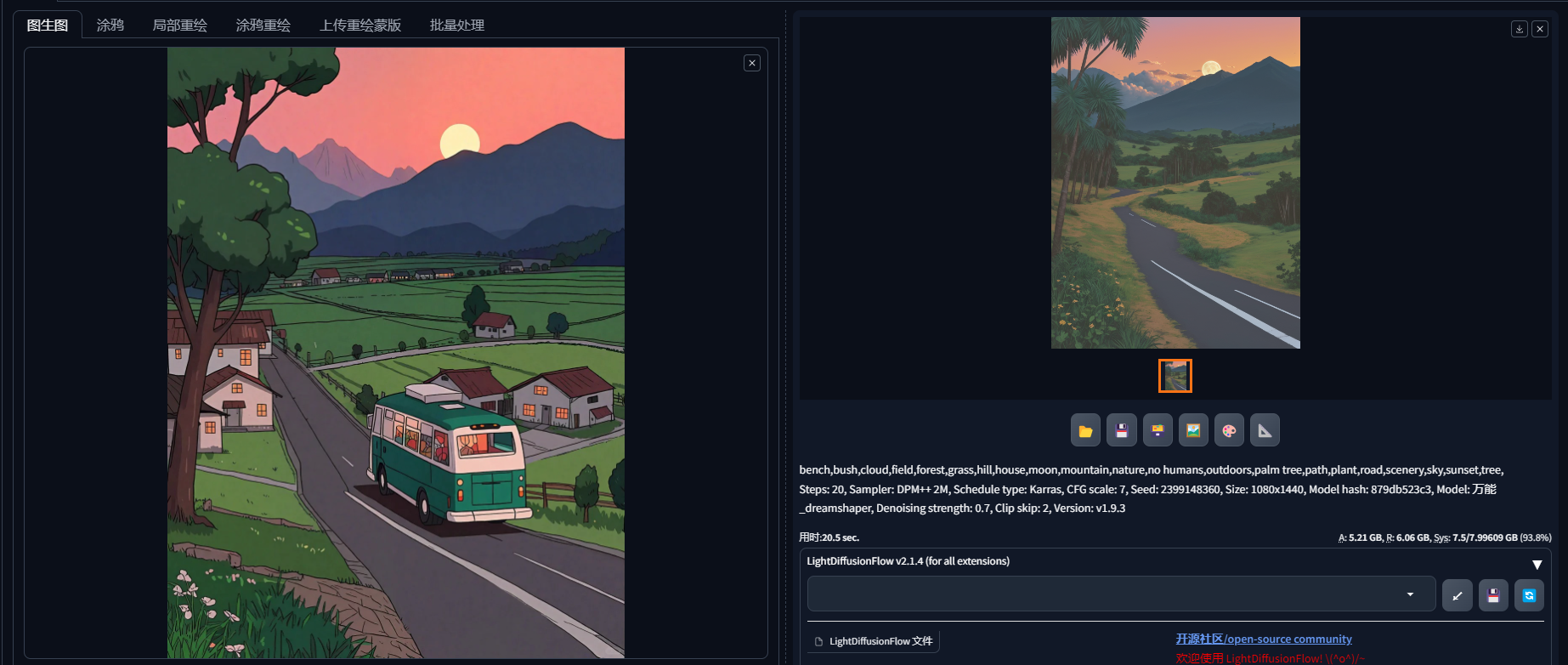
Stable Diffusion绘画 | 图生图-基础使用介绍—提示词反推
按默认设置直接出图 拖入图片值图生图框中,保持默认设置,直接生成图片,出图效果如下: 因为重绘幅度0.7,所出图片与原图有差异,但整体的框架构图与颜色与原图类似。 输入关键词后出图 在正向提示词中输入…...

正点原子imx6ull-mini-Linux驱动之Linux SPI 驱动实验(22)
跟上一章一样,其实这些设备驱动,无非就是传感器对应寄存器的读写。而这个读写是建立在各种通信协议上的,比如上一章的i2c,我们做了什么呢,就是把设备注册成一个i2c平台驱动,这个i2c驱动怎么搞的呢ÿ…...

TypeScript 函数
函数是JavaScript应用程序的基础。 它帮助你实现抽象层,模拟类,信息隐藏和模块。 在TypeScript里,虽然已经支持类,命名空间和模块,但函数仍然是主要的定义 行为 的地方。 TypeScript为JavaScript函数添加了额外的功能&…...

C++ : namespace,输入与输出,函数重载,缺省参数
一,命名空间(namespace) 1.1命名空间的作用与定义 我们在学习c的过程中,经常会碰到命名冲突的情况。就拿我们在c语言中的一个string函数来说吧: int strncat 0; int main() {printf("%d", strncat);return 0; } 当我们运行之后&…...

目标检测 | yolov1 原理和介绍
1. 简介 论文链接:https://arxiv.org/abs/1506.02640 时间:2015年 作者:Joseph Redmon 代码参考:https://github.com/abeardear/pytorch-YOLO-v1 yolo属于one-stage算法,仅仅使用一个CNN网络直接预测不同目标的类别与…...

excel中有些以文本格式存储的数值如何批量转换为数字
一、背景 1.1 文本格式存储的数值特点 在平时工作中有时候会从别地方导出来表格,表格中有些数值是以文本格式存储的(特点:单元格的左上角有个绿色的小标)。 1.2 文本格式存储的数值在排序时不符合预期 当我们需要进行排序的时候…...

原神升级计划数据表:4个倒计时可以修改提示信息和时间,可以点击等级、命座、天赋、备注进行修改。
<!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><title>原神倒计时</title><style>* {margin: 0;padding: 0;box-sizing: border-box;body {background: #0b1b2c;}}header {width: 100vw;heigh…...

YoloV10 论文翻译(Real-Time End-to-End Object Detection)
摘要 近年来,YOLO因其在计算成本与检测性能之间实现了有效平衡,已成为实时目标检测领域的主流范式。研究人员对YOLO的架构设计、优化目标、数据增强策略等方面进行了探索,并取得了显著进展。然而,YOLO对非极大值抑制࿰…...

第R1周:RNN-心脏病预测
本文为🔗365天深度学习训练营 中的学习记录博客 原作者:K同学啊 要求: 1.本地读取并加载数据。 2.了解循环神经网络(RNN)的构建过程 3.测试集accuracy到达87% 拔高: 1.测试集accuracy到达89% 我的环境&a…...

Golang | Leetcode Golang题解之第321题拼接最大数
题目: 题解: func maxSubsequence(a []int, k int) (s []int) {for i, v : range a {for len(s) > 0 && len(s)len(a)-1-i > k && v > s[len(s)-1] {s s[:len(s)-1]}if len(s) < k {s append(s, v)}}return }func lexico…...

远程连接本地虚拟机失败问题汇总
前言 因为我的 Ubuntu 虚拟机是新装的,并且应该装的是比较纯净的版本(纯净是指很多工具都尚未安装),然后在使用远程连接工具 XShell 连接时出现了很多问题,这些都是我之前没遇到过的(因为之前主要使用云服…...
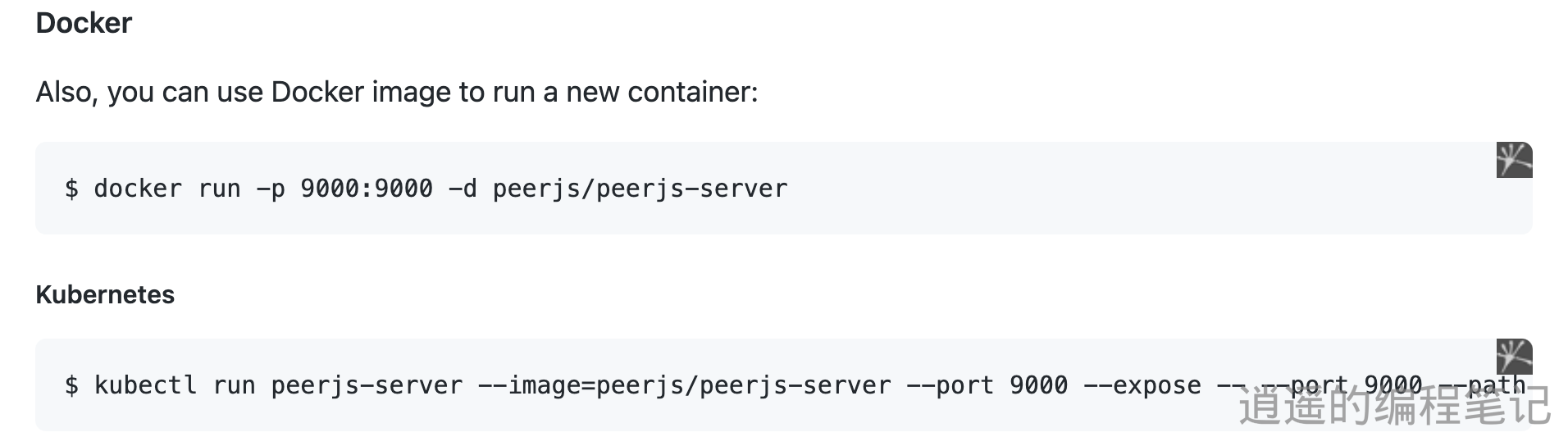
WebRTC 初探
前言 项目中有局域网投屏与文件传输的需求,所以研究了一下 webRTC,这里记录一下学习过程。 WebRTC 基本流程以及概念 下面以 1 对 1 音视频实时通话案例介绍 WebRTC 的基本流程以及概念 WebRTC 中的角色 WebRTC 终端,负责音视频采集、编解码、NAT 穿…...

Python:read,readline和readlines的区别
在Python中,read(), readline(), 和 readlines() 是文件操作中常用的三个方法,它们都用于从文件中读取数据,但各自的使用方式和适用场景有所不同。 read() 方法: read(size-1) 方法用于从文件中读取指定数量的字符。如果指定了si…...

重生之我学编程
编程小白如何成为大神?大学新生的最佳入门攻略 编程已成为当代大学生的必备技能,但面对众多编程语言和学习资源,新生们常常感到迷茫。如何选择适合自己的编程语言?如何制定有效的学习计划?如何避免常见的学习陷阱&…...
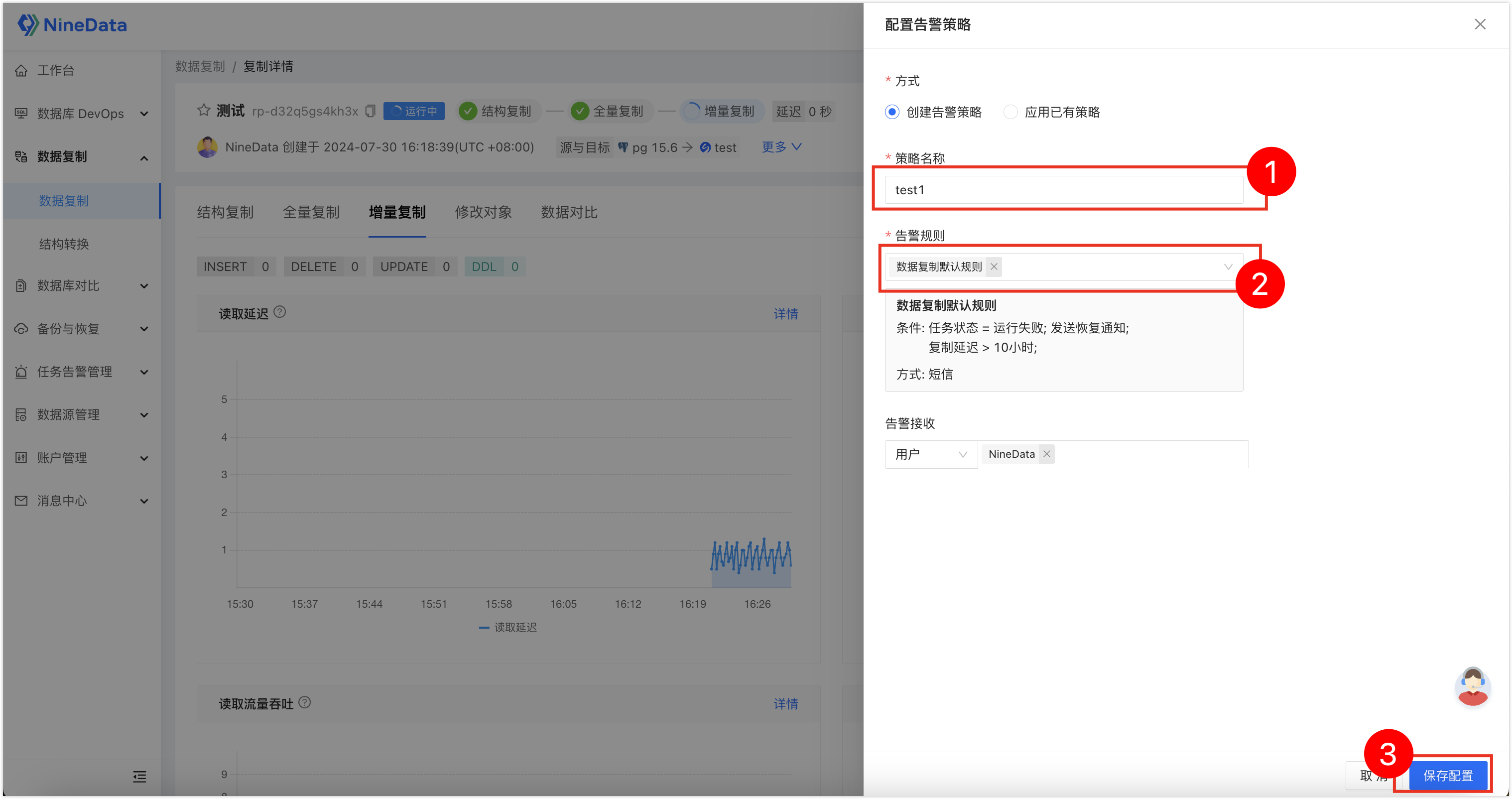
如何将PostgreSQL的数据实时迁移到SelectDB?
PostgreSQL 作为一个开源且功能强大的关系型数据库管理系统,在 OLTP 系统中得到了广泛应用。很多企业利用其卓越的性能和灵活的架构,应对高并发事务、快速响应等需求。 然而对于 OLAP 场景,PostgreSQL 可能并不是最佳选择。 为了实现庞大规…...

关于c语言的const 指针
const * type A 指向的数据是常量 如上所示,运行结果如下,通过解引用的方式,改变了data的值 const type * A 位置是常量,不能修改 运行结果如下 type const * A 指针是个常量,指向的值可以改变 如上所示,…...

万能门店小程序开发平台功能源码系统 带完整的安装代码包以及安装搭建教程
互联网技术的迅猛发展和用户对于便捷性需求的不断提高,小程序以其轻量、快捷、无需安装的特点,成为了众多商家和开发者关注的焦点。为满足广大商家对于门店线上化、智能化管理的需求,小编给大家分享一款“万能门店小程序开发平台功能源码系统…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...
