OpenCV入门(十八)快速学会OpenCV 17 直线检测
OpenCV入门(十八)快速学会OpenCV 17 直线检测
- 1.霍夫直线变换概述
- 2.霍夫变换原理
- 3.操作实例
- 3.1 HoughLines函数
- 3.2 HoughLinesP函数
作者:Xiou
1.霍夫直线变换概述
霍夫变换是一种在图像中寻找直线、圆形以及其他简单形状的方法。霍夫变换采用类似于投票的方式来获取当前图像内的形状集合,该变换由Paul Hough(霍夫)于1962年首次提出。最初的霍夫变换只能用于检测直线,经过发展后,霍夫变换不仅能够识别直线,还能识别其他简单的图形结构,常见的有圆、椭圆等。
霍夫直线变换用来在图像内寻找直线,在OpenCV中,可以用函数cv2.HoughLines()和函数cv2.HoughLinesP()实现。
霍夫变换 (Hough Line Transform) 是图像处理中的一种特征提取技术. 通过平面空间到极值坐标空间的转换, 可以帮助我们实现直线检测。
2.霍夫变换原理
为了方便说明问题,先以我们熟悉的笛卡儿坐标系(与笛卡儿空间对应)为例来说明霍夫变换的基本原理。与笛卡儿坐标系对应,我们构造一个霍夫坐标系(对应于霍夫空间)。在霍夫坐标系中,横坐标采用笛卡儿坐标系中直线的斜率k,纵坐标使用笛卡儿坐标系中直线的截距b。
首先,我们观察笛卡儿空间中的一条直线在霍夫空间内的映射情况。例如,在图16-1中,左图是笛卡儿x-y坐标系(笛卡儿空间),右图是霍夫k-b坐标系(霍夫空间)。在笛卡儿空间中,存在着一条直线y=k0x+b0,该直线的截距k0是已知的常量,截距b0也是已知的常量。将该直线映射到霍夫空间内,找到已知的点(k0, b0),即完成映射。
从上述分析中可知,笛卡儿空间内的一条直线,其斜率为k,截距为b,映射到霍夫空间内成为一个点(k, b)。或者,可以这样理解,霍夫空间内的一个点(k0, b0),映射到笛卡儿空间,就是一条直线y=k0x+b0。
当我们把直线 y = kx + b 画在指标坐标系上, 如下图. 我们再从原点引线段到直线上的任一点。

我们可以得到这条线段与 x 轴的夹角为 θ, 距离是 r. 对于直线上的任一点 (x0, y0), 我们可以得到公式:

综上所述,在霍夫空间内,经过一个点的直线越多,说明其在笛卡儿空间内映射的直线,是由越多的点所构成(穿过)的。我们知道,两个点就能构成一条直线。但是,如果有一个点是因为计算错误而产生的,那么它和另外一个点,也会构成一条直线,此时就会凭空构造出一条实际上并不存在的直线。这种情况是要极力避免的。因此,在计算中,我们希望用更多的点构造一条直线,以提高直线的可靠性。也就是说,如果一条直线是由越多点所构成的,那么它实际存在的可能性就越大,它的可靠性也就越高。因此,霍夫变换选择直线的基本思路是:选择有尽可能多直线交汇的点。
3.操作实例
3.1 HoughLines函数
OpenCV提供了函数cv2.HoughLines()用来实现霍夫直线变换,该函数要求所操作的源图像是一个二值图像,所以在进行霍夫变换之前要先将源图像进行二值化,或者进行Canny边缘检测。
函数cv2.HoughLines()的语法格式为:
lines=cv2.HoughLines(image, rho, theta, threshold)
式中:
● image是输入图像,即源图像,必须是8位的单通道二值图像。如果是其他类型的图像,在进行霍夫变换之前,需要将其修改为指定格式。
● rho为以像素为单位的距离r的精度。一般情况下,使用的精度是1。
● theta为角度θ的精度。一般情况下,使用的精度是π/180,表示要搜索所有可能的角度。
● threshold是阈值。该值越小,判定出的直线就越多。通过上一节的分析可知,识别直线时,要判定有多少个点位于该直线上。在判定直线是否存在时,对直线所穿过的点的数量进行评估,如果直线所穿过的点的数量小于阈值,则认为这些点恰好(偶然)在算法上构成直线,但是在源图像中该直线并不存在;如果大于阈值,则认为直线存在。所以,如果阈值较小,就会得到较多的直线;阈值较大,就会得到较少的直线。
● 返回值lines中的每个元素都是一对浮点数,表示检测到的直线的参数,即(r, θ),是numpy.ndarray类型。
有一点需要强调的是,使用函数cv2.HoughLines()检测到的是图像中的直线而不是线段,因此检测到的直线是没有端点的。所以,我们在进行霍夫直线变换时所绘制的直线都是穿过整幅图像的。
代码实例:
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取图像
img = cv2.imread('tes.jpg')
# 转换成灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 边缘检测, Sobel算子大小为3
edges = cv2.Canny(gray, 50, 150, apertureSize=3)
orgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
oShow = orgb.copy()
# 霍夫曼直线检测
lines = cv2.HoughLines(edges, 1, np.pi / 180, 140)#遍历
for line in lines:# 获取rho和thetarho, theta = line[0]a = np.cos(theta)b = np.sin(theta)x0 = a * rhoy0 = b * rhox1 = int(x0 + 1000 * (-b))y1 = int(y0 + 1000 * (a))x2 = int(x0 - 1000 * (-b))y2 = int(y0 - 1000 * (a))cv2.line(orgb, (x1, y1), (x2, y2), (0, 0, 255), 2)
#展示
plt.subplot(121)
plt.imshow(oShow)
plt.axis('off')
plt.subplot(122)
plt.imshow(orgb)
plt.axis('off')
输出结果:

3.2 HoughLinesP函数
OpenCV提供了函数cv2.HoughLines()用来实现霍夫直线变换,此函数在 HoughLines 的基础上末尾加了一个代表概率 (Probabilistic) 的 P, 表明它可以采用累计概率霍夫变换, 来找出二值图像中的直线。
该函数要求所操作的源图像是一个二值图像,所以在进行霍夫变换之前要先将源图像进行二值化,或者进行Canny边缘检测。函数cv2.HoughLinesP()的语法格式为:
lines=cv2.HoughLinesP(image, rho, theta, threshold)
参数:
image: 输入图像
rho: 线性搜索半径步长, 以像素为单位
theta: 线性搜索步长, 以弧度为单位
threshold: 累计阈值
minLineLength: 最短直线长度
maxLineGap: 最大孔隙距离
代码实例:
import numpy as np
import cv2
from matplotlib import pyplot as plt# 读取图片
image = cv2.imread("tes.jpg")
image_copy = image.copy()# 转换成灰度图
image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)# 边缘检测, Sobel算子大小为3
edges = cv2.Canny(image_gray, 170, 220, apertureSize=3)# 霍夫曼直线检测
lines = cv2.HoughLinesP(edges, 1, np.pi / 180, 100, minLineLength=100, maxLineGap=10)# 遍历
for line in lines:# 获取坐标x1, y1, x2, y2 = line[0]cv2.line(image_copy, (x1, y1), (x2, y2), (0, 0, 255), thickness=5)# 图片展示
f, ax = plt.subplots(2, 2, figsize=(12, 12))# 子图
ax[0, 0].imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
ax[0, 1].imshow(image_gray, "gray")
ax[1, 0].imshow(edges, "gray")
ax[1, 1].imshow(cv2.cvtColor(image_copy, cv2.COLOR_BGR2RGB))# 标题
ax[0, 0].set_title("original")
ax[0, 1].set_title("image gray")
ax[1, 0].set_title("image edge")
ax[1, 1].set_title("image line")plt.show()输出结果:


相关文章:

OpenCV入门(十八)快速学会OpenCV 17 直线检测
OpenCV入门(十八)快速学会OpenCV 17 直线检测1.霍夫直线变换概述2.霍夫变换原理3.操作实例3.1 HoughLines函数3.2 HoughLinesP函数作者:Xiou 1.霍夫直线变换概述 霍夫变换是一种在图像中寻找直线、圆形以及其他简单形状的方法。霍夫变换采用…...
nginx快速入门.跟学B站nginx一小时精讲课程笔记
nginx快速入门.跟学B站nginx一小时精讲课程笔记nginx简介及环境准备nginx简介环境准备一、nginx 安装1.使用yum安装2.常用命令3.使用systemctl启动、停止、重新加载4.配置文件5.配置文件结构二、配置静态web1.静态网页配置2.listen监听3.server_name4.location三、HTTP反向代理…...
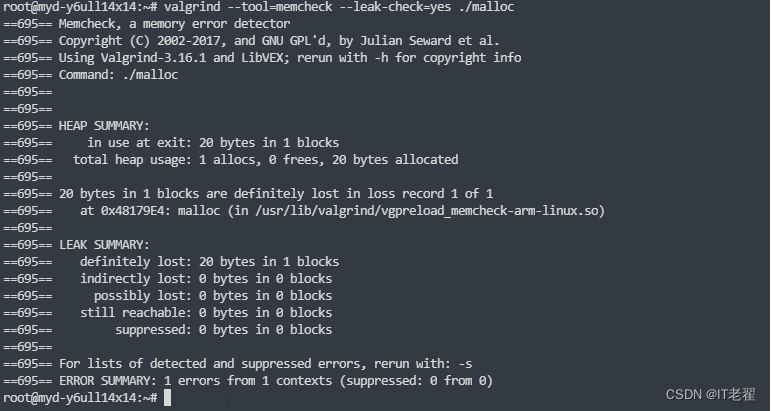
内存泄漏定位工具之 valgrind
内存泄漏检测工具 文章目录内存泄漏检测工具一、valgrind介绍1. memcheck2. cachegrind3. helgrind二、源码下载三、命令操作1.memcheck 工具四、虚拟机下使用1. x86编译2. 正常程序测试3. 申请内存不释放测试4. 内存越界的测试5. 读写已经释放的内存五、ARM平台使用1.交叉编译…...
Django(一)安装
好久没更新了 学习的内容太多了有点杂 一时不知道从何说起 !!! 对于Django我也不是很了解 在网上搜了个词条就是以下显示 我目前的了解也仅限于此 希望在接下来的学习过程中 有更多的学习体会可以和大家分享 一涉及到在对应python环境 下载东西时思维就会很混乱 这里再把之前…...
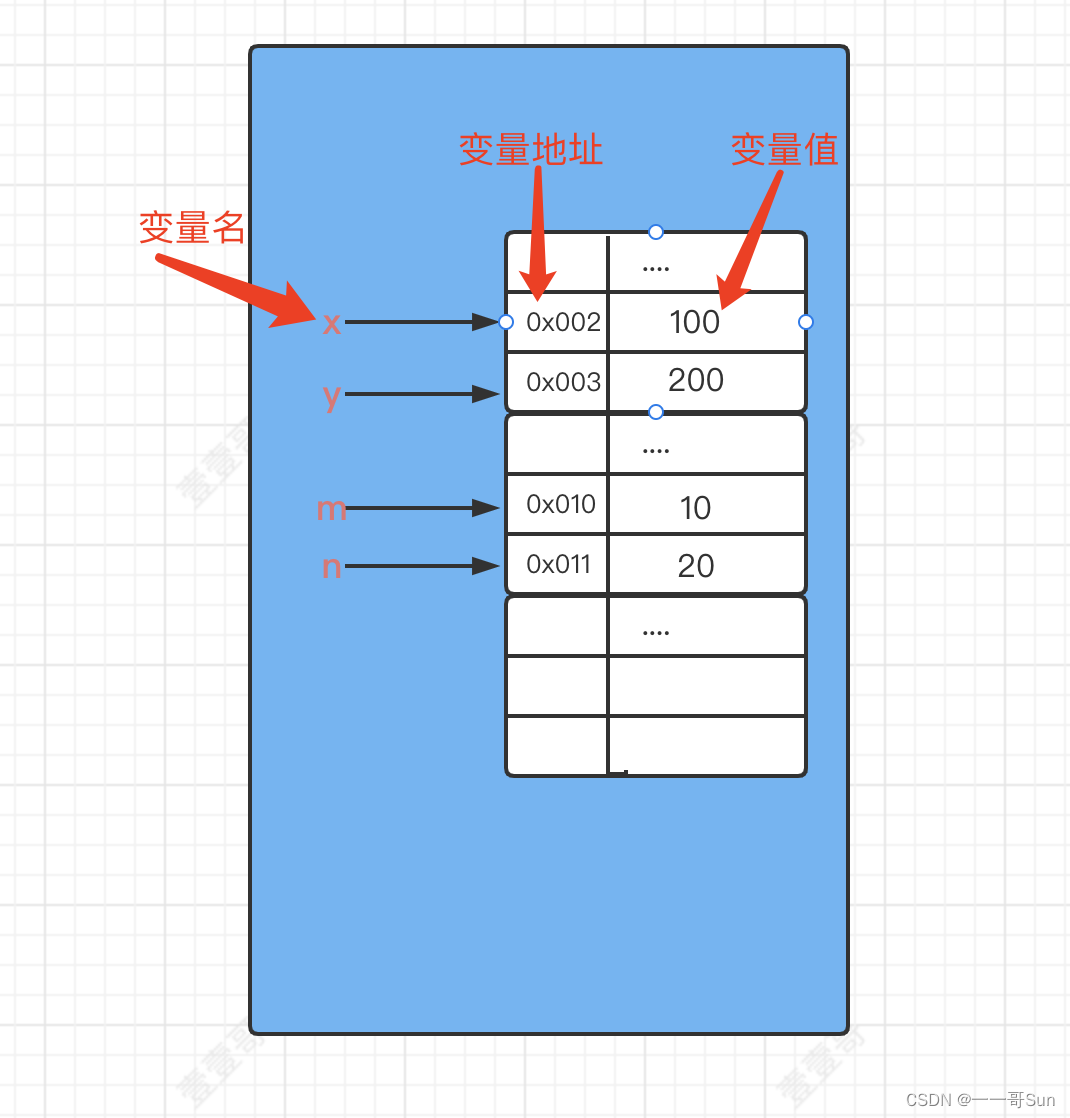
11从零开始学Java之如何正确地定义变量?
作者:孙玉昌,昵称【一一哥】,另外【壹壹哥】也是我哦CSDN博客专家、万粉博主、阿里云专家博主、掘金优质作者前言在之前的文章中,壹哥给大家讲解了Java的第一个案例HelloWorld,并详细给大家介绍了Java的标识符…...
51单片机之喝水提醒器
定时器定时器介绍晶振晶体震荡器,又称数字电路的“心脏”,是各种电子产品里面必不可少的频率元器件。数字电路的所有工作都离不开时钟,晶振的好坏、晶振电路设计的好坏,会影响到整个系统的稳定性。时钟周期时钟周期也称为振荡周期…...
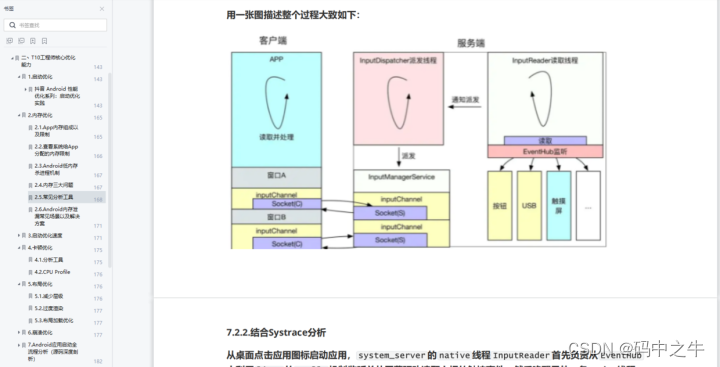
扒一扒抖音是如何做线程优化的
背景 最近在对一些大厂App进行研究学习,在对某音App进行研究时,发现其在线程方面做了一些优化工作,并且其解决的问题也是之前我在做线上卡顿优化时遇到的,因此对其具体实现方案做了深入分析。本文是对其相关源码的研究加上个人理…...

149.网络安全渗透测试—[Cobalt Strike系列]—[重定器/代理服务器/流量走向分析]
我认为,无论是学习安全还是从事安全的人多多少少都会有些许的情怀和使命感!!! 文章目录一、Cobalt Strike 重定器1、Cobalt Strike 重定器简介2、重定器用到的端口转发工具二、cobalt strike重定器实验1、实验背景2、实验过程3、流…...

Qt调用Chrome浏览器
一、前言 最近有个小项目需要跳转网页,之前有了解过,但是没有在项目中使用过Qt网页嵌入; 结合自己之前的博客,有如下两种技术可以实现我的需求: 1、Qt–网页嵌入 2、Qt使用QAxWidget调用Windows组件 但是在实际开…...
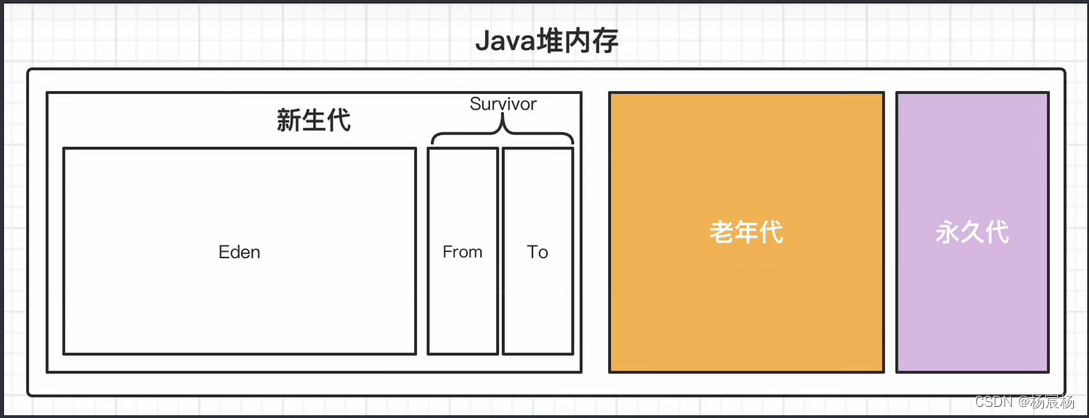
JVM虚拟机垃圾回收机制
JVM虚拟机垃圾回收机制垃圾回收机制判断是否存活算法引用计数法可达性分析法最终判定垃圾回收算法分代收集机制空间分配担保垃圾回收机制 判断是否存活算法 java语言和我们之前学的c/c不同,c/c可以手动进行内存释放,那样随时随地就可以释放不必要的内存…...

菜鸟刷题Day3
⭐作者:别动我的饭 ⭐专栏:菜鸟刷题 ⭐标语:悟已往之不谏,知来者之可追 一.字符串压缩:面试题 01.06. 字符串压缩 - 力扣(LeetCode) 描述 字符串压缩。利用字符重复出现的次数,编…...

南京邮电大学数据库第三次课后作业
1.单选(2分) 下列关于模式的术语中,(C)不是指数据库三级模式结构中的外模式 (A)子模式 (B)用户模式 (C)存储模式 (D)用户视图 2单选题(2分) 数据库的三级模式结构中,描述数据全局逻辑…...
【vue2】使用vue常见的业务流程与实现思路
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:vue的业务处理思路。前台数据渲染与后台的增删改查操作 【前言】当大家会点开这一篇文章…...

Linux操作系统ARM体系结构处理器机制原理与实现
ARM 的概念ARM(Advanced RISC Machine),既可以认为是一个公司的名字,也可以认为是对一类微处理器的通称,还可以认为是一种技术的名字。ARM 公司并不生产芯片也不销售芯片,它只出售芯片技术授权。其合作公司针对不同需求搭配各类硬…...

Mongodb 常用基本语法与操作
常用操作 1、 Help查看命令提示 db.help(); 2、 切换/创建数据库 use test 如果数据库不存在,则创建数据库,否则切换到指定数据库 3、 查询所有数据库 show dbs; 4、 删除当前使用数据库 db.dropDatabase(); 5、 查看当前使用的数据库 db.getName(); 6、…...

MySQL注入秘籍【绕过篇】
MySQL注入秘籍【绕过篇】1.通用方法2.绕过空格3.绕过引号4.绕过逗号,5.绕过等号6.绕过and/or7.绕过注释符8.绕过函数检测1.通用方法 编码 编码无非就是hex、url等等编码,让传到数据库的数据能够解析的即可,比如URL编码一般在传给业务的时候就会自动解码…...
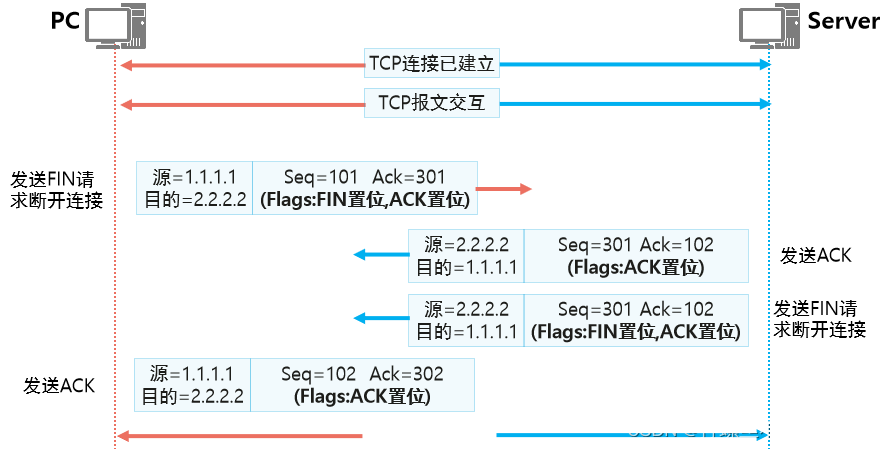
TCP三次握手/四次挥手
TCP三次握手 任何基于TCP的应用,在发送数据之前,都需要由TCP进行“三次握手”建立连接示意图 第一次握手:客户端PC发送一个SYN位置1(SYN1代表请求服务端建立连接)的TCP报文发送给要建立TCP连接的Server,此…...

Python程序员看见一个好看的手机壁纸网站,开撸!
人生苦短,我用python 最近好像没什么大事, .那就采集一下小——姐——姐————看下吧~ python 安装包资料:点击此处跳转文末名片获取 最近有同学的爬虫代码出了bug,给问我怎么改 于是就发现了这个好看的手机壁纸网站。 这个图片应该是违规…...
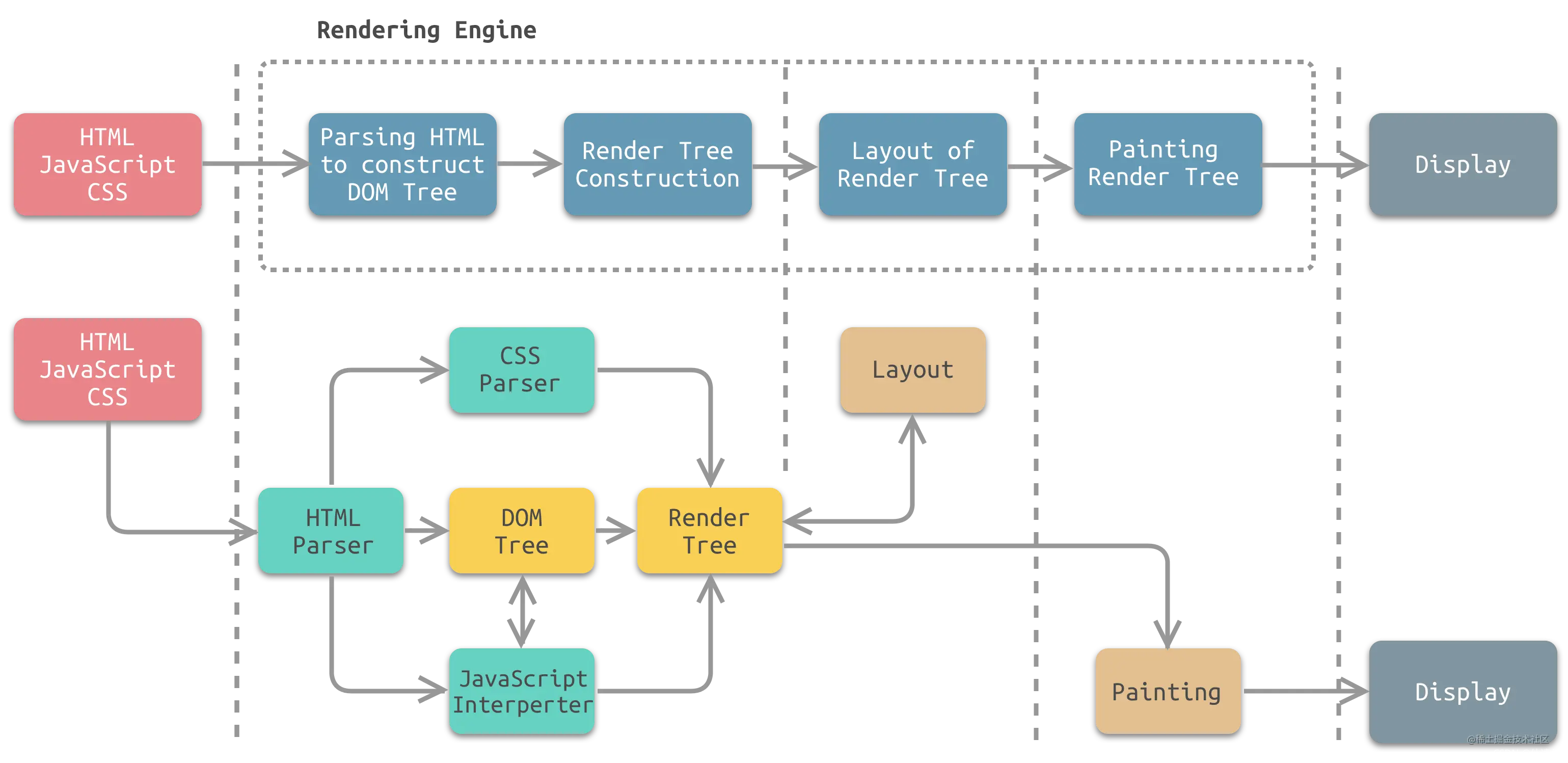
浏览器工作原理
一、JavaScript 的历史 JavaScript(简称JS)Web前端开发的脚本语言。 它诞生1995年,由网景公司的 Brendan Eich 开发。最初,JavaScript 被设计用于在网页上嵌入动态内容和交互式功能。 1996年,JavaScript 1.1 成为国…...

对在使用容器HashSet存放自定义对象时重写其类的hashcode和equals方法的几点认识
判断是否是相同对象时,hashcode和equals方法的调用顺序 先调用hashcode()方法,再调用equals()方法如果hashcode()方法得到的哈希值不同,那么两个对象一定不相同,不作后续判断如果hashcode()方法得到的哈希值相同,那么…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
