BTC连续拉涨,击碎空头幻想
原创 | 刘教链
隔夜BTC继续拉涨,急破6万刀,“过了黄洋界,险处不须看”,一度逼近63k,目前暂于61-62k区间休整。从8月5日极限插针下探49k,仅仅3天多时间,就连续拉涨到了61k,总涨幅接近25%。
不知道这种3天拉涨25%的机会,一年里能有几次,一个人的整个投资生涯中又能满仓把握住几次?所以,教链在8月5号暴跌恐慌之际,于当日文章《暴跌,洗牌!》中直言不讳地写道:
劝人割肉,非蠢即坏。
如果一个小白,害怕之时听了割肉的鼓动,在49k清仓,那么仅仅3天后,在61k买回,就立即损失接近1/5的BTC,也就是损失了20%的仓位。5个BTC割肉,3天之后还剩4个BTC。
3天损失1个BTC。
而如果他不买回,那么随着BTC的继续拉涨,他的损失将越来越大。等BTC升至98k,他将损失一半的BTC。但就算BTC再次探低到49k,他可能依旧不敢买回,因为那个时候,一定会有更多的声音告诉他,BTC还将继续下跌,30k、20k、……
最后的结局,很可能是他永远失去仓位,失去BTC。
待到8月7号,教链又在《大跌见真金,BTC还能再创新高吗?》一文中,复盘2020年“312”和2021年“519”的暴跌模式,对照分析本次洗盘。文中指出:「如果说,今年2024年在BTC周期上的时空位置,更接近2020年的话,那么从概率上讲,押韵“312”的可能性或许会更大一些。」
再到昨晚[8月8号教链内参“空头是否已三振出局?”],教链进一步对2021年“519”暴跌模式进行了细细的品味,重温了2021年7月22日所写的《空头三振出局》一文。
请注意《空头三振出局》的发表时间点。标记到K线图上来看一下:
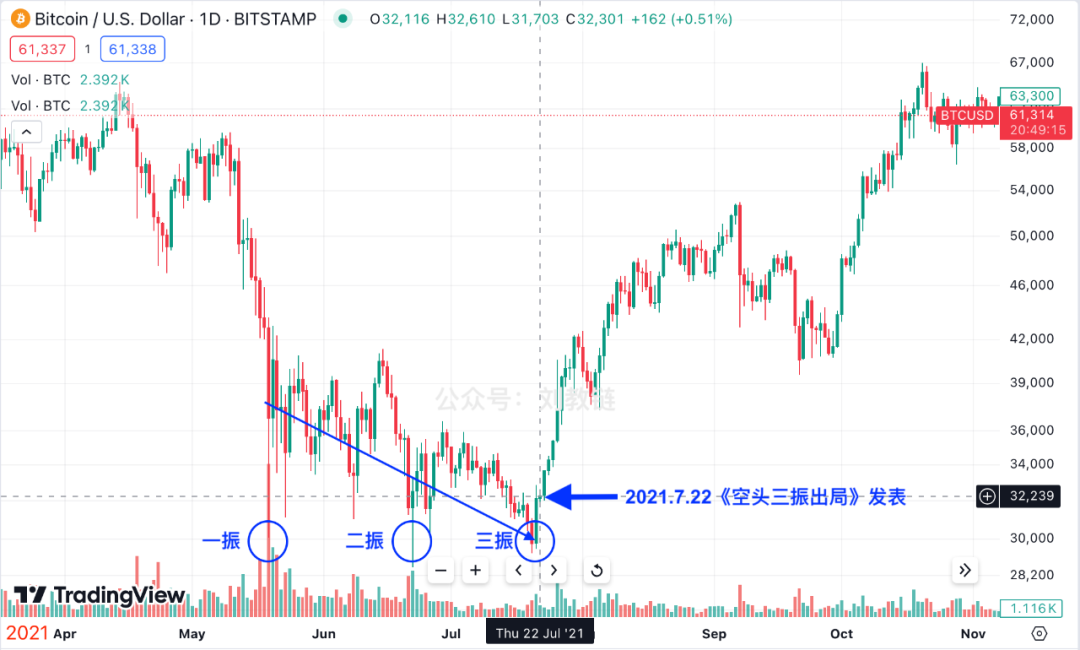
在2021年7月22号的时候看这个图,可不是上图这样子的,而是下图这样子的:
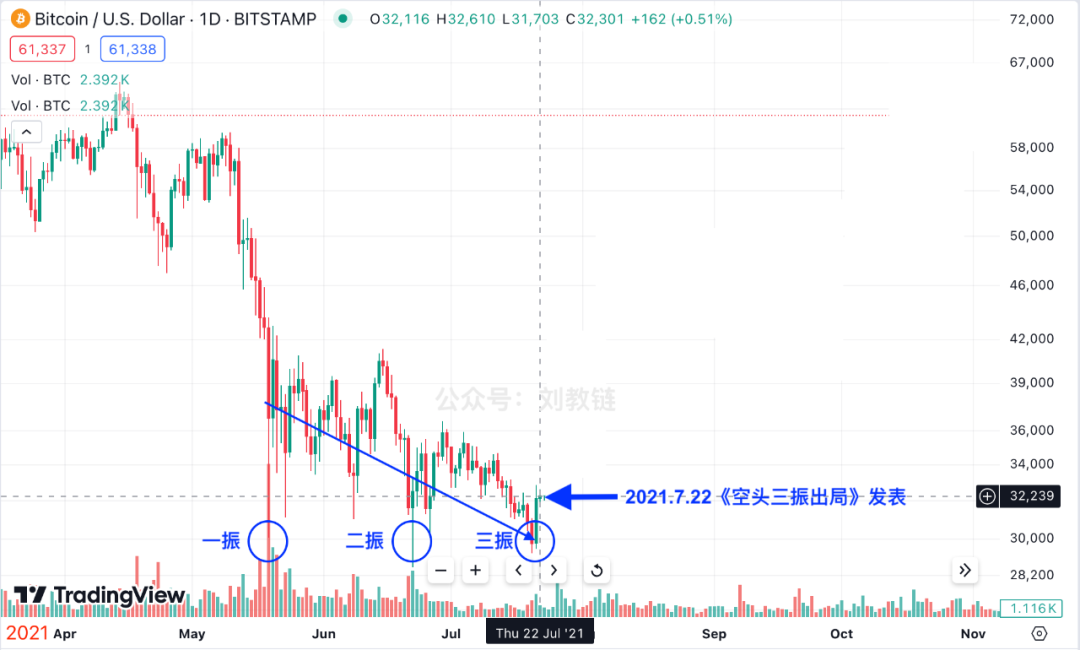
因此,昨晚[“8.8教链内参:空头是否已三振出局?”]翻译一下就是:
8.5暴跌也许并非“519”,而是“722”?
这无疑是一个极为大胆的假设。
在“信仰-怀疑”阶段,多空观点的交锋必然是激烈的。
自从2024年3月13-14日BTC局部触顶73.8k之后,至今已经洗盘5个月。
如果参考当年黄金ETF上市后,局部触顶后长达10个月的洗盘期,那么目前BTC依然是“半渡”。
黄金ETF洗盘通道,在7个月前教链2024.1.9文章《比特币大伏大起》中给出了图示:
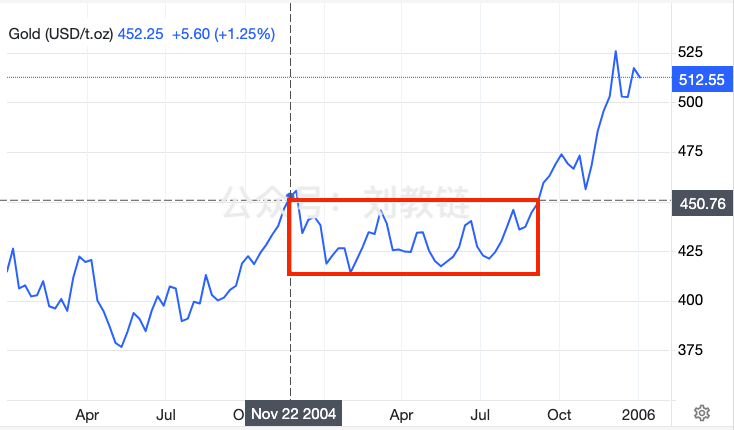
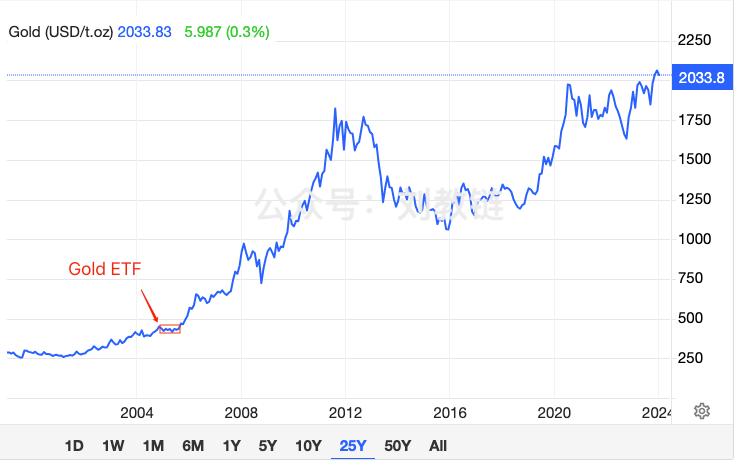
不管是三振也好,五振也罢,通过[“8.5教链内参:全球暴跌之下,教链评估BTC的几个关键点位”]中的评估测试,可以几乎肯定的是,空头对3万刀甚至2.5万刀乃至于本轮牛市已结束的幻想,是终将要随着BTC的不断续创新高而被击得粉碎的了。

7月内参合订本 & 8.8内参:空头是否已三振出局?

内参,请加入刘教链的知识星球:

* * *
延伸刘教链精彩文章:
【攻略】币圈破产指南 2019.6.15
小杂感 2021.6.30
牛市熊了么? 2021.7.6
下雨和交易 2021.6.25
不动如山,方得始终 2021.1.13
比特币趋势大反转 2024.5.16
春江水暖鸭先知 2021.6.4
草根的力量,庶民的胜利 2023.11.9
比特币天天向上 2023.1.30
(公众号:刘教链。知识星球:公众号回复“星球”)
(免责声明:本文内容均不构成任何投资建议。加密货币为极高风险品种,有随时归零的风险,请谨慎参与,自我负责。)
喜欢本文就请点亮在看、点赞、转发支持哦
👇👇👇
相关文章:

BTC连续拉涨,击碎空头幻想
原创 | 刘教链 隔夜BTC继续拉涨,急破6万刀,“过了黄洋界,险处不须看”,一度逼近63k,目前暂于61-62k区间休整。从8月5日极限插针下探49k,仅仅3天多时间,就连续拉涨到了61k,总涨幅接近…...

【Spring】Sping笔记01
参考学习:b站浪飞yes ---------------------------------------------------- # 一、Spring 引入 **事务实现** java public class EmployeeServiceImpl implements IEmployeeService { public void save(Employee employee){ // 打开资源 /…...

Gridcontrol纵向/横向合并单元格
指定列值相同,纵向合并: this.gridView1.OptionsView.AllowCellMerge true;//启用合并列 // 启用指定合并列事件 this.gridView1.CellMerge new DevExpress.XtraGrid.Views.Grid.CellMergeEventHandler(gridView1_CellMerge);#region 合并指定的列 pri…...

从周杰伦的《青花瓷》三次更名看方文山的国学情怀与工匠精神
《青花瓷》三次更名,方文山的国学情怀与工匠精神 在华语乐坛上,周杰伦与方文山的合作堪称黄金组合,他们的作品不仅引领了流行音乐的潮流,更让传统文化焕发出新的生机。在这其中,《青花瓷》无疑是他们合作的经典之一&a…...
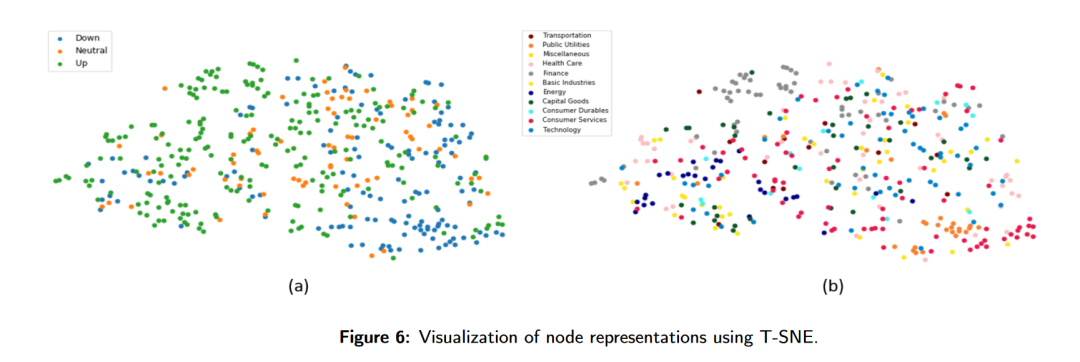
HATS:分层图注意力神经网络用于股票预测
HATS:分层图注意力神经网络用于股票预测 原创 QuantML QuantML 2024年08月09日 19:08 上海 Content 本文提出了一种名为HATS(Hierarchical Graph Attention Network)的分层图注意力网络,用于预测股市动向。HATS通过选择性地聚合…...

【日常记录-MySQL】MySQL设置root用户密码
Author:赵志乾 Date:2024-08-09 Declaration:All Right Reserved!!! 1. 简介 MySQL8.0.30安装后启动,发现root用户尚未设置密码。以下是两种设置root用户密码的方式。 2. 示例 2.1 mysqladmin…...
)
高级Web安全技术(第二篇)
我们继续第二篇,继续深入了解web的安全 一、概述 在Web应用的开发与部署中,安全问题不仅是技术挑战,更是对系统整体架构的考验。本篇文章将继续深入探讨高级Web安全技术,重点关注API安全的最佳实践、OAuth的安全实施以及安全编码…...

前端实现文件下载常用几种方式
项目中前端下载一般分为两种情况: 后端直接提供一个文件地址,通过浏览器打开就可以下载。需要发送请求,后端返回二进制流数据,前端解析流数据,生成URL实现下载。 前端对应的实质是a标签和Blob文件下载,这…...
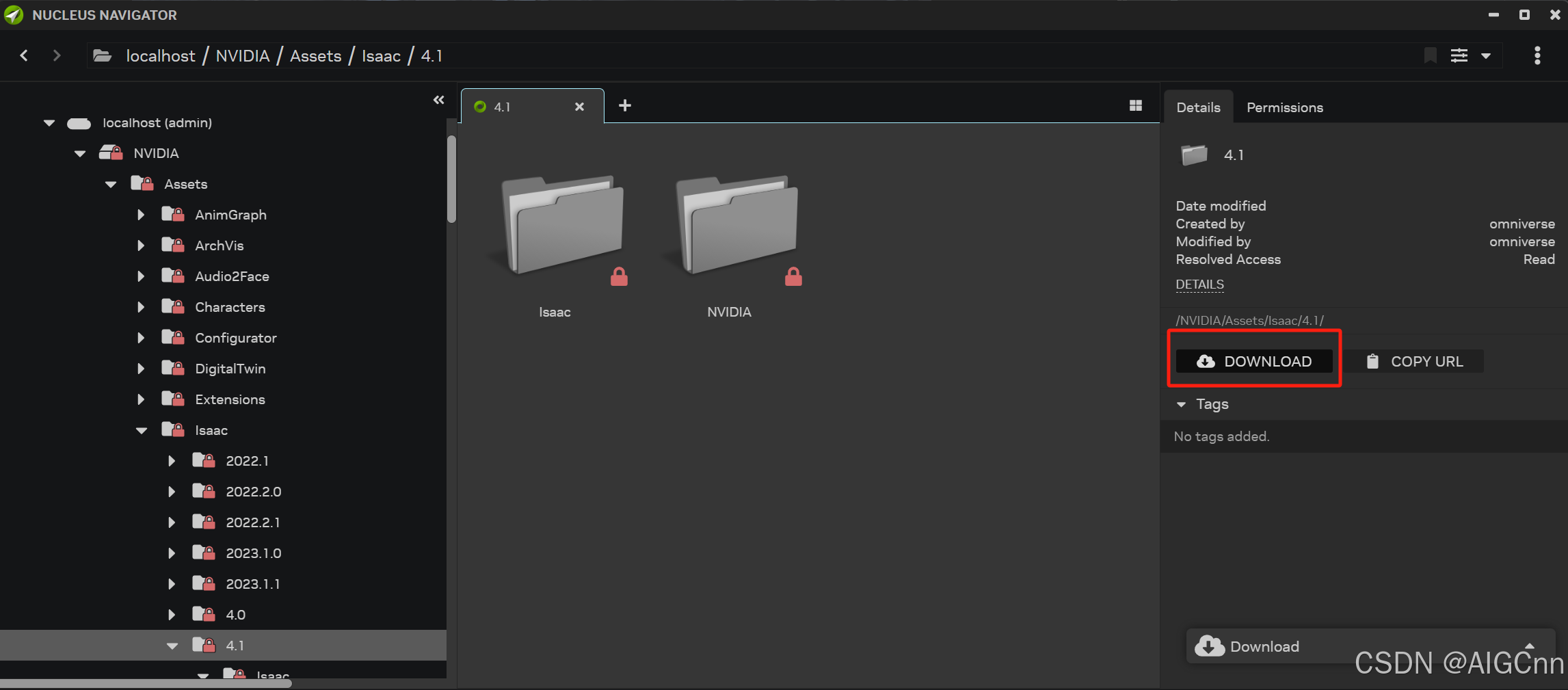
Isaac Lab 安装 (ubuntu22.04环境)
Windows下的安装见这篇博客: Isaac Lab 安装与初体验 (windows环境)-CSDN博客 ubuntu22.04下的安装与windows下十分类似,还是参考官方的,Installation using Isaac Sim Binaries Installation using Isaac Sim Bina…...

todoList清单(HTML+CSS+JavaScript)
🌏个人博客主页: 前言: 前段时间学习了JavaScript,然后写了一个todoList小项目,现在和大家分享一下我的清单以及如何实现的,希望对大家有所帮助 🔥🔥🔥文章专题ÿ…...

LVS集群实现四层负载均衡详解(以nat,dr模式为例)
目录 一、LVS集群的介绍 1、LVS 相关术语: 2、lvs四层负载均衡工作原理 3、相关名词概念 4、lvs集群的类型 二、lvs的nat模式 1、介绍: 2、数据逻辑: 3、nat实验部署 环境搭建: 1、lvs中要去打开内核路由功能,…...

七夕表白网页效果实现与解析
七夕是中国传统的情人节,是一个充满浪漫与爱的节日。在这个特别的日子里,用代码来表达心意也是一种独特且有趣的方式。本篇文章将带你一步步实现一个简单但充满心意的七夕表白网页。通过使用HTML、CSS和少量的JavaScript,我们将创建一个包含跳…...
课程11-自然语言处理之NLP的语言模型-seq2seq模型,seq+注意力与代码详解)
人工智能算法工程师(高级)课程11-自然语言处理之NLP的语言模型-seq2seq模型,seq+注意力与代码详解
大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(高级)课程11-自然语言处理之NLP的语言模型-seq2seq模型,seq+注意力,word2vec与代码详解。本课程面向高级人工智能算法工程师,深入讲解自然语言处理(NLP)中的关键语言模型技术,包括seq2seq模型及其增强版加入注意力…...

从PyTorch官方的一篇教程说开去(6.2 - 张量 tensor 矩阵运算等)
您的进步和反馈是我写作最大的动力,小伙伴来个三连呗!共勉~ 话不多说,书接上文,需要温习的小伙伴请移步 - 从PyTorch官方的一篇教程说开去(6.1 - 张量 tensor 基本操作)-CSDN博客 借图镇楼 - 1 - 矩阵乘…...

【网络层】直连路由、静态路由、动态路由
文章目录 路由表直连路由直连路由 技术背景直连路由 实战训练 静态路由静态路由 技术背景静态路由 概述静态路由 配置命令静态路由 实战训练 动态路由动态路由 技术背景路由协议概述路由协议分类 路由表 路由表的形成,路由的来源: 路由来源备注直连路由…...

tkinter用法总结
Tkinter 是 Python 标准库中的一个模块,用于创建图形用户界面 (GUI)。它是 Python 中最常用的 GUI 库之一,因为它集成在 Python 的标准发行版中,无需额外安装即可使用。 一、基本用法 1. 简单示例 import tkinter as tk# 创建主窗口 root …...

iOS基础-Block
系列文章目录 文章目录 系列文章目录一、Block是什么二、Block的使用场景1. 异步操作和完成处理器2. 动画3. 集合操作4. 定时器5. 自定义控件的事件处理6.错误处理 三、Block的底层实现1.结构分析2.Block的类型3.Block的copy4.变量捕捉 四、Block的使用细节1.auto变量的生命周期…...

本地图片瀑布流浏览器asonry Image Viewer
本地图片瀑布流浏览器asonry Image Viewer 前言效果图部分源码领取完整源码下期更新 前言 一款采用 HTML 的瀑布流本地图片浏览器「Masonry Image Viewer」只需要把你的图片文件夹拖到下载的 index 网页文件里面就可以实现瀑布流效果。项目免费开源,据介绍采用了HT…...

macos重装系统 启动U盘制作方法 - createinstallmedia 命令使用方法总结
macos重装系统比windows要稍微复杂一些,不过还好,macos系统安装app这个Apple官方提供的系统软件里面默认就内置了一个可用为我们制作启动盘的工具 createinstallmedia 我们下载的apple安装镜像要门是 dmg/pkg/iso 的压缩档案格式的,要么是 x…...
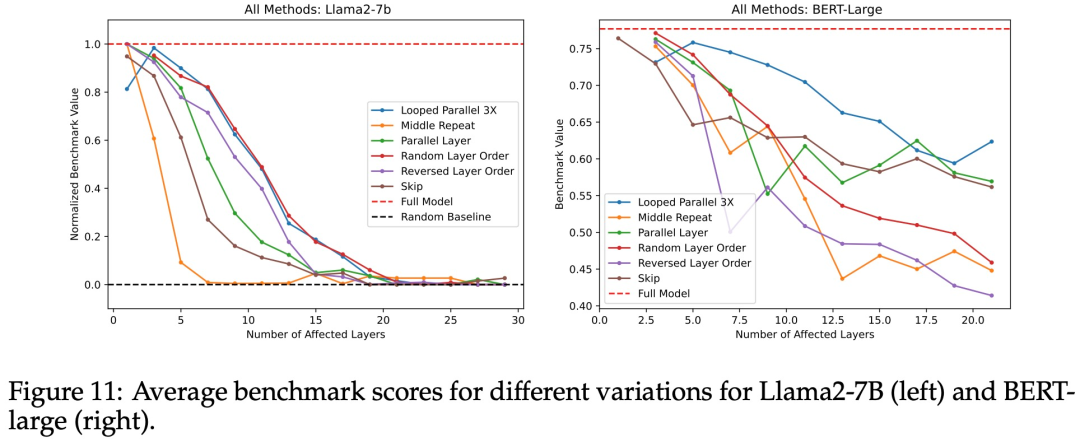
八问八答搞懂Transformer内部运作原理
最近这一两周看到不少互联网公司都已经开始秋招提前批了。 不同以往的是,当前职场环境已不再是那个双向奔赴时代了。求职者在变多,HC 在变少,岗位要求还更高了。 最近,我们又陆续整理了很多大厂的面试题,帮助一些球友…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
