【数据结构】六、图:4.图的遍历(深度优先算法DFS、广度优先算法BFS)
三、基本操作
文章目录
- 三、基本操作
- 1.图的遍历
- 1.1 深度优先遍历DFS
- 1.1.1 DFS算法
- 1.1.2 DFS算法的性能分析
- 1.1.3 深度优先的生成树和生成森林
- 1.2 广度优先遍历BFS
- 1.2.1 BFS算法
- 1.2.2 BFS算法性能分析
- 1.2.3 广度优先的生成树和生成森林
- 1.3 图的遍历与图的连通性
1.图的遍历
图的遍历是和树的遍历类似,我们希望从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次, 这一过程就叫做图的遍历(Traversing Graph)。
对于图的遍历来,通常有两种遍历次序方案:
- 深度优先遍历
- 广度优先遍历
1.1 深度优先遍历DFS
深度优先遍历(Depth First Search),也有称为深度优先搜索,简称为DFS。
1.1.1 DFS算法
深度优先搜索类似于树的先序遍历。如其名称中所暗含的意思一样,这种搜索算法所遵循的搜索策略是尽可能“深”地搜索一个图,每次都尝试向更深的节点走。它的基本思想如下:
首先访问图中某一起始顶点v,然后由v出发,访问与v邻接且未被访问的任一顶点w1,再访问与 w1 邻接且未被访问的任一顶点…重复上述过程。当不能再继续向下访问时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问过,则从该点开始继续上述搜索过程,直至图中所有顶点均被访问过为止。

先序遍历:12563478
DFS 最显著的特征在于其 递归调用自身。同时与 BFS 类似,DFS 会对其访问过的点打上访问标记,在遍历图时跳过已打过标记的点,以确保 每个点仅访问一次。符合以上两条规则的函数,便是广义上的 DFS。算法过程如下:
bool visited[MAX_VERTEX_NUM]; //访问标记数组//从顶点出发,深度优先遍历图G
void DFS(Graph G, int v){visit(v); //访问顶点visited[v] = TRUE; //设已访问标记//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点,若有则返回顶点号,否则返回-1。//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点,返回除w外顶点vfor(int w = FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)){if(!visited[w]){ //w为v的尚未访问的邻接顶点DFS(G, w);//递归}}
}
但是如果是非连通图,那么就不能从一个结点遍历所有的结点。这个时候需要添加一个函数来寻找没被访问的结点。
//深度遍历算法final
bool visited[MAX_VERTEX_NUM]; //访问标记数组//从顶点出发,深度优先遍历图G
void DFS(Graph G, int v){visit(v); //访问顶点visited[v] = TRUE; //设已访问标记//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点,若有则返回顶点号,否则返回-1。//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点,返回除w外顶点vfor (int w = FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)){if (!visited[w]){ //w为v的尚未访问的邻接顶点DFS(G, w);//递归}}
}//对图进行深度优先遍历
void DFSTraverse(MGraph G){for (int v=0; v<G.vexnum; v++){visited[v] = FALSE; //初始化已访问标记数据}for (int v=0; v<G.vexnum; v++){ //从v=0开始遍历if(!visited[v]){DFS(G, v);}}
}
1.1.2 DFS算法的性能分析
空间复杂度:DFS算法是一个递归算法,需要借助一个递归工作栈。最坏情况是 O(|V|)。

时间复杂度:
- 邻接矩阵:需要访问|V|个结点,然后查找|V|个结点的邻接点|V|个,那么时间复杂度为 O(|V|+|V|2)。
O(|V|2) - 邻接表:需要访问|V|个结点,然后查找每个结点的邻接点总共需要O(2|E|)时间,那么时间复杂度为 O(|V|+2|E|)。
O(|V|+|E|)
1.1.3 深度优先的生成树和生成森林
对一个图进行所有结点的遍历,那么在这个遍历过程中不是所有的边都被用到:

**【注意】**1. 从不同的点出发,得到的遍历序列不一样;即使从同一个点出发,也可能得到不同的遍历序列。
- 因为邻接矩阵的表示方式是唯一的,所以DFS算法得到的遍历序列是唯一的。但是因为单链表的表示方式不是唯一的,所以DFS算法得到的遍历序列不是唯一的。
当图里面有多个连通分量,那么就会有多个生成树,这时候这些树就组成一个生成森林。

1.2 广度优先遍历BFS
广度优先遍历(Breadth First Search),又称为广度优先搜索,简称BFS。
1.2.1 BFS算法
如果说图的深度优先遍历类似树的前序遍历,那么图的广度优先遍历就类似于树的层序遍历了。
广度优先搜索是一种分层的查找过程,每向前走一步可能访问一批顶点,不像深度优先搜索那样有往回退的情况,因此它不是一个递归的算法。为了实现逐层的访问,算法必须借助一个辅助队列,以记忆正在访问的顶点的下一层顶点。

以下是广度优先遍历的代码:
从结点v出发遍历:
//邻接矩阵的广度遍历算法。从结点v出发遍历
void BFS(MGraph G, int v){Queue Q;//把所有结点全部标记为false,表示没有访问过for(int i = 0; i<G.numVertexes; i++){visited[i] = FALSE;}InitQueue(&Q); //初始化一辅助用的队列visit(v); //访问顶点vivited[v] = TRUE; //设置当前访问过EnQueue(&Q, v); //将此顶点入队列//若当前队列不为空while(!QueueEmpty(Q)){DeQueue(&Q, &v); //顶点v出队列//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点,若有则返回顶点号,否则返回-1。//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点,返回除w外顶点v//把出队结点的相邻的所有结点入队for(int w=FirstNeighbor(G, v); w>=0; w=NextNeighbor(G, v, w)){//检验v的所有邻接点if(!visited[w]){visit(w); //访问顶点wvisited[w] = TRUE; //访问标记EnQueue(&Q, w); //顶点w入队列}//if}//for}//while
}
但是如果是非连通图,那么就不能从一个结点遍历所有的结点。这个时候需要添加一个函数来寻找没被访问的结点。
//邻接矩阵的广度遍历算法final
void BFSTraverse(MGraph G){int i, j;Queue Q;//把所有结点全部标记为false,表示没有访问过for(i = 0; i<G.numVertexes; i++){visited[i] = FALSE;}InitQueue(&Q); //初始化一辅助用的队列for(i=0; i<G.numVertexes; i++){ //这里是从0开始//若是未访问过就处理if(!visited[i]){//下面的部分相当于前面写的BFS(G, v);visit(i); //访问顶点vivited[i] = TRUE; //设置当前访问过EnQueue(&Q, i); //将此顶点入队列//若当前队列不为空while(!QueueEmpty(Q)){DeQueue(&Q, &i); //顶点i出队列//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点,若有则返回顶点号,否则返回-1。//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点,返回除w外顶点v//把出队结点的相邻的所有结点入队for(j=FirstNeighbor(G, i); j>=0; j=NextNeighbor(G, i, j)){//检验v的所有邻接点if(!visited[j]){visit(j); //访问顶点jvisited[j] = TRUE; //访问标记EnQueue(Q, j); //顶点j入队列}//if}//for}//while}//if}//for
}
下面的部分相当于前面写的BFS(G, v);,所以还有一种写法是把BFSTraverse 和 BFS分开。
//对非连通图的广度遍历算法final
void BFSTraverse(MGraph G){Queue Q;InitQueue(&Q); //初始化一辅助用的队列int i;//把所有结点全部标记为false,表示没有访问过for(i=0; i<G.numVertexes; i++){visited[i] = FALSE;}for(i=0; i<G.numVertexes; i++){ //这里是从0开始//若是未访问过就处理if(!visited[i]){BFS(G, i); //调用BFS函数}//if}//for
}void BFS(MGraph G, int v){visit(v); //访问顶点vivited[v] = TRUE; //设置当前访问过EnQueue(&Q, v); //将此顶点入队列//若当前队列不为空while(!QueueEmpty(Q)){DeQueue(&Q, &v); //顶点i出队列//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点,若有则返回顶点号,否则返回-1。//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点,返回除w外顶点v//把出队结点的相邻的所有结点入队for(w=FirstNeighbor(G, v); w>=0; w=NextNeighbor(G, v, w)){//检验v的所有邻接点if(!visited[w]){visit(w); //访问顶点wvisited[w] = TRUE; //访问标记EnQueue(Q, w); //顶点w入队列}//if}//for}//while
}
对于无向图,调用BFS函数的次数 = 连通分量。
1.2.2 BFS算法性能分析
空间复杂度:最坏情况是当所有结点都连在第一个结点上,辅助队列大小为 O(|V|)。
时间复杂度:
- 邻接矩阵:需要访问|V|个结点,然后查找|V|个结点的邻接点|V|个,那么时间复杂度为 O(|V|+|V|2)。
O(|V|2) - 邻接表:需要访问|V|个结点,然后查找每个结点的邻接点总共需要O(2|E|)时间,那么时间复杂度为 O(|V|+2|E|)。
O(|V|+|E|)
1.2.3 广度优先的生成树和生成森林
对一个图进行所有结点的遍历,那么在这个遍历过程中不是所有的边都被用到:

【注意】因为邻接矩阵的表示方式是唯一的,所以BFS算法得到的遍历序列是唯一的。但是因为单链表的表示方式不是唯一的,所以BFS算法得到的遍历序列不是唯一的。

当图里面有多个连通分量,那么就会有多个生成树,这时候这些树就组成一个生成森林。
1.3 图的遍历与图的连通性
图的遍历算法可以用来判断图的连通性。
-
对于无向图进行BFS/DFS遍历。
调用BFS/DFS函数的次数 = 连通分量数。
- 若是连通图的,则从任一结点出发, 仅需一次遍历就能够访问图中的所有顶点,只需调用1次BFS/DFS。
- 若是非连通的,则从某一个顶点出发,一次遍历只能访问到该顶点所在连通分量的所有顶点,而对于图中其他连通分量的顶点,则无法通过这次遍历访问。
-
对于有向图进行BFS/DFS遍历。
调用BFS/DFS函数的次数要具体问题具体分析- 若起始顶点到其他各顶点都有路径,则只需调用1次BFS/DFS函数,对于强连通图,从任一结点出发都只需调用1次BFS/DFS。
- 但是从起始顶点不能到达所有结点,那么需要调用多次BFS/DFS。
相关文章:

【数据结构】六、图:4.图的遍历(深度优先算法DFS、广度优先算法BFS)
三、基本操作 文章目录 三、基本操作1.图的遍历1.1 深度优先遍历DFS1.1.1 DFS算法1.1.2 DFS算法的性能分析1.1.3 深度优先的生成树和生成森林 1.2 广度优先遍历BFS1.2.1 BFS算法1.2.2 BFS算法性能分析1.2.3 广度优先的生成树和生成森林 1.3 图的遍历与图的连通性 1.图的遍历 图…...

29、号外!号外!ERA5再分析数据下载方式更新啦
文章目录 1. 前言2. 账号注册与协议签署2.1 账号注册2.2 签署CDS-Beta使用条款2.3 更新.cdsapi文件 3. 常见问题与解决方法(持续更新中)3.1 问题1:更新完.cdsapi文件之后,原有下载代码不可以使用3.2 问题2: RuntimeError: 403 Cli…...

智能识别,2024年SD卡数据恢复软件的智能进化
除了手机之外现在有不少的设备还是依靠SD卡来存储数据,比如相机、摄像头、无人机等。有的时候会因为一些意外的情况导致数据丢失,那是真的丢失了吗?大部分情况还是可以依靠sd卡数据恢复工具来找回这些“消失”的数据哦。 1.福昕数据恢复 链…...

浙大数据结构慕课课后题(04-树5 Root of AVL Tree)
题目要求: AVL 树是一种自平衡的二叉搜索树。在 AVL 树中,任何节点的两个子子树的高度最多相差一;如果在任何时候它们相差不止一,则进行重新平衡以恢复此属性。图 1-4 说明了旋转规则。 图1 图2 图3 图4 现在给定一系列插入,您应该…...

Golang | Leetcode Golang题解之第331题验证二叉树的前序序列化
题目: 题解: func isValidSerialization(preorder string) bool {n : len(preorder)slots : 1for i : 0; i < n; {if slots 0 {return false}if preorder[i] , {i} else if preorder[i] # {slots--i} else {// 读一个数字for i < n &&…...

zdppy+vue3+onlyoffice文档管理系统项目实战 20240812上课笔记
遗留问题 1、增加新建和导入按钮,有按钮了,但是还没有完善,图标还不对,需要解决 2、登录功能 3、用户管理 4、角色管理 5、权限管理 6、分享功能 解决新建和导入的图标问题 解决代码: <a-button type"prim…...

怎么将mov视频转换成mp4?将mov视频转换成mp4的方法
怎么将mov视频转换成mp4?由于mov格式通常与苹果设备兼容性较好,而mp4则更广泛地支持于各种播放器和设备中,因此将mov转换为mp4可以确保视频在更多场景下能够流畅播放。通过这种转换,你可以确保视频在各种平台和设备上的兼容性&…...

大数据技术——实战项目:广告数仓(第五部分)
目录 第9章 广告数仓DIM层 9.1 广告信息维度表 9.2 平台信息维度表 9.3 数据装载脚本 第10章 广告数仓DWD层 10.1 广告事件事实表 10.1.1 建表语句 10.1.2 数据装载 10.1.2.1 初步解析日志 10.1.2.2 解析IP和UA 10.1.2.3 标注无效流量 10.2 数据装载脚本 第9章 广…...

计算机毕业设计 家电销售展示平台 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

C# 根据MySQL数据库中数据,批量删除OSS上的垃圾文件
protected void btndeleteTask_Click(object sender, EventArgs e){//获取标识为已删除数据,一次加载500条int countlocks _goodsItemsApplication.CountAllNeedExecuteTask();int totalPagelocks (countlocks 500 - 1) / 500;//分批次处理for (int curentpage …...

Vue3+Element-plus+setup使用vuemap/vue-amap实现高德地图API相关操作
首先要下载依赖并且引入 npm安装 // 安装核心库 npm install vuemap/vue-amap --save// 安装loca库 npm install vuemap/vue-amap-loca --save// 安装扩展库 npm install vuemap/vue-amap-extra --save cdn <script src"https://cdn.jsdelivr.net/npm/vuemap/vue-a…...
Windows配置开机直达桌面并跳过锁屏登录界面在 Windows 10 中添加在启动时自动运行的应用
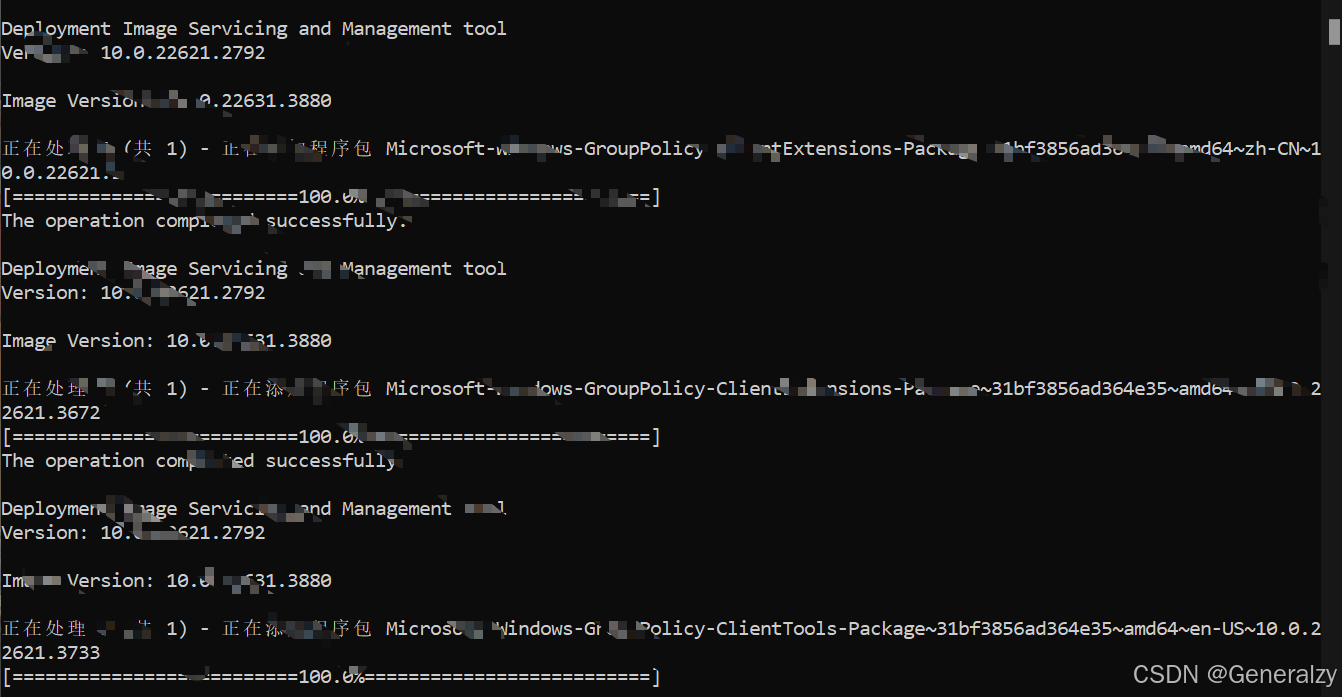
目录 Win10开机直达桌面并跳过锁屏登录界面修改组策略修改注册表跳过登录界面 在 Windows 10 中添加在启动时自动运行的应用设置系统级别服务一、Windows下使用sc将应用程序设置为系统服务1. 什么是sc命令?2. sc命令的基本语法3. 创建Windows服务的步骤与示例创建服…...
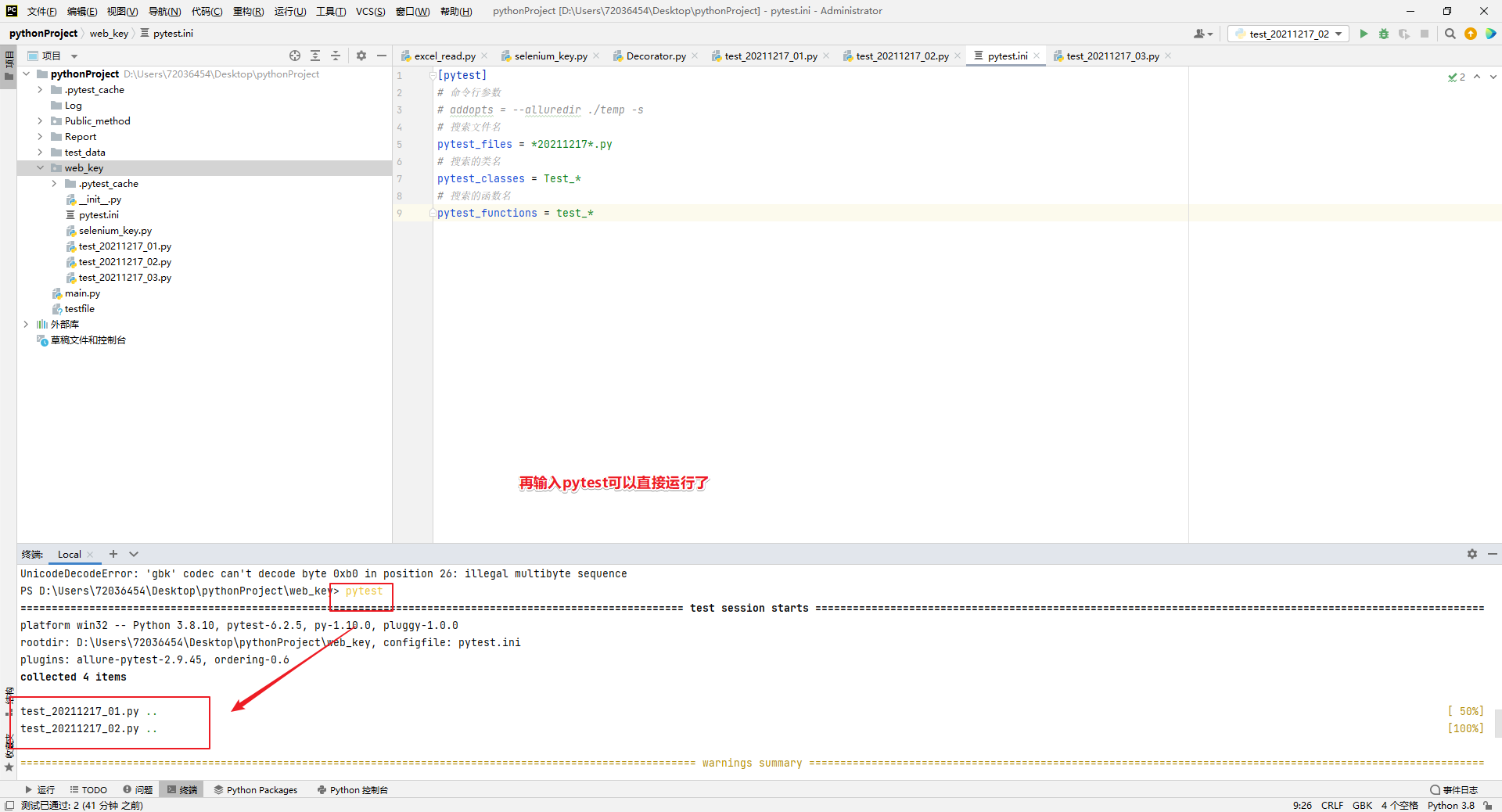
pythonUI自动化007::pytest的组成以及运行
pytest组成: 测试模块:以“test”开头或结尾的py文件 测试用例:在测试模块里或测试类里,名称符合test_xxx函数或者示例函数。 测试类:测试模块里面命名符合Test_xxx的类 函数级: import pytestclass Test…...

开放式耳机哪个品牌好用又实惠?五大口碑精品分享
如今开放式耳机市场日益火爆,不少知名品牌都在对产品进行升级迭代,那么如何在一众品牌型号中选择到自己最满意的那一款呢?开放式耳机哪个品牌好用又实惠?这就需要更专业的选购攻略,因此笔者专门整理出了专业机构的开放…...
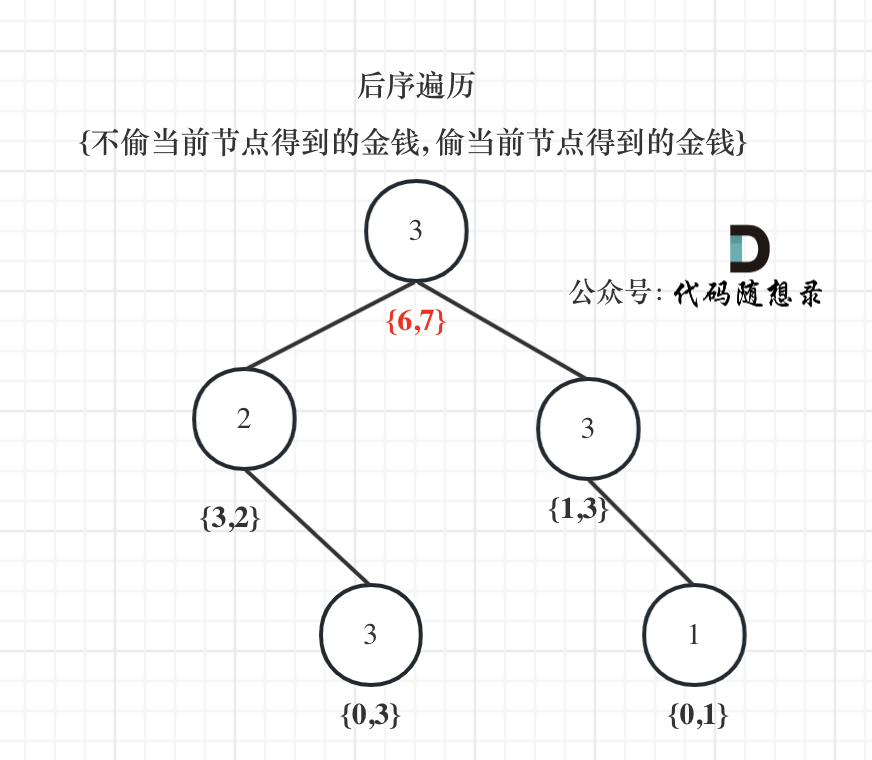
代码随想录算法训练营day39||动态规划07:多重背包+打家劫舍
多重背包理论 描述: 有N种物品和一个容量为V 的背包。 第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。 求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。 本质: …...

WebSocket革新:用PHP实现实时Web通信
标题:WebSocket革新:用PHP实现实时Web通信 在现代Web应用中,实时通信是一个不可或缺的功能。WebSocket作为一种在单个TCP连接上进行全双工通信的协议,它允许服务器主动向客户端推送数据,极大地简化了客户端和服务器之…...

Python教程(十三):常用内置模块详解
目录 专栏列表1. os 模块2. sys 模块3. re 模块4. json 模块5. datetime 模块6. math 模块7. random 模块8. collections 模块9. itertools 模块10. threading 模块11. 加密 模块 总结 专栏列表 Python教程(十):面向对象编程(OOP…...

Linux 下的进程状态
文章目录 一、运行状态运行队列运行状态和运行队列 二、睡眠状态S状态D状态D状态产生的原因 三、暂停状态T状态t 状态 四、僵尸状态为什么有僵尸状态孤儿进程 一、运行状态 R状态:进程已经准备好随时被调度了。 运行队列 每个 CPU 都会维护一个自己的运行队列&am…...

【设计模式】六大基本原则
文章目录 开闭原则里氏替换原则依赖倒置原则单一职责原则接口隔离原则迪米特原则总结 开闭原则 核心就一句话:对扩展开放,对修改关闭。 针对的目标可以是语言层面的类、接口、方法,也可以是系统层面的功能、模块。当需求有变化的时候&#…...

Selenium网页的滚动
网页滚动功能实现 网页的滚动 如果需要对网页进行滑动操作,可以借助浏览器对象调用execute_script()方法来执行js语句,从而实现网页中的滚动下滑操作。 使用js语法实现网页滚动: # 根据x轴和y轴的值来定向滚动对应数值的距离 window.scrol…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
