浙大数据结构慕课课后题(04-树5 Root of AVL Tree)
题目要求:
AVL 树是一种自平衡的二叉搜索树。在 AVL 树中,任何节点的两个子子树的高度最多相差一;如果在任何时候它们相差不止一,则进行重新平衡以恢复此属性。图 1-4 说明了旋转规则。

图1

图2

图3

图4
现在给定一系列插入,您应该分辨生成的 AVL 树的根。
输入规格:
每个输入文件都包含一个测试用例。对于每种情况,第一行都包含一个正整数N(<=20),这是要插入的键的总数。然后N不同的整数键在下一行中给出。一行中的所有数字都用空格分隔。
输出规格:
对于每个测试用例,将生成的 AVL 树的根打印在一行中。
示例输入 1:
5
88 70 61 96 120
示例输出 1:
70
题解:
思路如注释所示,可通过所有测试点。
#include<bits/stdc++.h>
using namespace std;
typedef struct AVLNode *Position;
typedef Position AVLTree;
typedef int ElementType;
struct AVLNode{ElementType Data;AVLTree Left;AVLTree Right;int Hight;
}; int Max(int a,int b){return a > b ? a:b;
}int GetHight(AVLTree A)
{return A == NULL ? -1 : A->Hight;
}AVLTree SingleLeftRotation(AVLTree A){AVLTree B = A->Left;A->Left = B->Right;B->Right = A;A->Hight = Max( GetHight(A->Left), GetHight(A->Right) ) + 1;B->Hight = Max( GetHight(B->Left), A->Hight ) + 1;return B;
}AVLTree SingleRightRotation(AVLTree A){AVLTree B = A->Right;A->Right = B->Left;B->Left = A;A->Hight = Max( GetHight(A->Left), GetHight(A->Right) ) + 1;B->Hight = Max( GetHight(B->Right), A->Hight ) + 1;return B;
}AVLTree DoubleLeftRightRotation(AVLTree A){/* 注意:A必须有一个左子结点B,且B必须有一个右子结点C *//* 将A、B与C做两次单旋,返回新的根结点C *//* 将B与C做右单旋,C被返回 */A->Left = SingleRightRotation(A->Left);/* 将A与C做左单旋,C被返回 */return SingleLeftRotation(A);
}AVLTree DoubleRightLeftRotation(AVLTree A){A->Right = SingleLeftRotation(A->Right);return SingleRightRotation(A);
}AVLTree Insert(AVLTree T,ElementType X){if(!T){ //若插入空树。则新建一个结点 T = (AVLTree)malloc(sizeof(struct AVLNode));T->Data = X;T->Hight = 0;T->Left = NULL;T->Right = NULL;} else if(X < T->Data){ //插入左树 T->Left = Insert(T->Left,X);if(GetHight(T->Left)-GetHight(T->Right) == 2){ //出现不平衡 if(X < T->Left->Data)T = SingleLeftRotation(T); //插入在左树的左边->单左旋elseT = DoubleLeftRightRotation(T); //插入再左树的右边->左右双旋 }}else if(X > T->Data){ //插入右树T->Right = Insert(T->Right,X);if(GetHight(T->Right)-GetHight(T->Left) == 2){ //出现不平衡 if(X > T->Right->Data)T = SingleRightRotation(T); //单右旋 elseT = DoubleRightLeftRotation(T); //右左旋 }} else return T;T->Hight = Max(GetHight(T->Left),GetHight(T->Right))+1;return T;
}int main(){AVLTree T = NULL;int t;cin>>t;while(t--){int num;cin>>num;T = Insert(T,num);}cout<<T->Data;
}此题有以下几个要注意的点:
1.Hight是指把 一个给定结点作为根节点时,其代表的树的树高,这样当左右子树树高差大于等于2时,可以发现平衡树失衡。
2.树高取左右子树的最大值。
3.左右双旋的时候在代码层面实际是先右单旋再左单旋,右左单旋时同理。
这里感觉何老师的ppt很清晰,(引一下,侵删)重点是找到“麻烦结点”对“不平衡发现者”是怎样破环的




相关文章:

浙大数据结构慕课课后题(04-树5 Root of AVL Tree)
题目要求: AVL 树是一种自平衡的二叉搜索树。在 AVL 树中,任何节点的两个子子树的高度最多相差一;如果在任何时候它们相差不止一,则进行重新平衡以恢复此属性。图 1-4 说明了旋转规则。 图1 图2 图3 图4 现在给定一系列插入,您应该…...

Golang | Leetcode Golang题解之第331题验证二叉树的前序序列化
题目: 题解: func isValidSerialization(preorder string) bool {n : len(preorder)slots : 1for i : 0; i < n; {if slots 0 {return false}if preorder[i] , {i} else if preorder[i] # {slots--i} else {// 读一个数字for i < n &&…...

zdppy+vue3+onlyoffice文档管理系统项目实战 20240812上课笔记
遗留问题 1、增加新建和导入按钮,有按钮了,但是还没有完善,图标还不对,需要解决 2、登录功能 3、用户管理 4、角色管理 5、权限管理 6、分享功能 解决新建和导入的图标问题 解决代码: <a-button type"prim…...

怎么将mov视频转换成mp4?将mov视频转换成mp4的方法
怎么将mov视频转换成mp4?由于mov格式通常与苹果设备兼容性较好,而mp4则更广泛地支持于各种播放器和设备中,因此将mov转换为mp4可以确保视频在更多场景下能够流畅播放。通过这种转换,你可以确保视频在各种平台和设备上的兼容性&…...

大数据技术——实战项目:广告数仓(第五部分)
目录 第9章 广告数仓DIM层 9.1 广告信息维度表 9.2 平台信息维度表 9.3 数据装载脚本 第10章 广告数仓DWD层 10.1 广告事件事实表 10.1.1 建表语句 10.1.2 数据装载 10.1.2.1 初步解析日志 10.1.2.2 解析IP和UA 10.1.2.3 标注无效流量 10.2 数据装载脚本 第9章 广…...

计算机毕业设计 家电销售展示平台 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

C# 根据MySQL数据库中数据,批量删除OSS上的垃圾文件
protected void btndeleteTask_Click(object sender, EventArgs e){//获取标识为已删除数据,一次加载500条int countlocks _goodsItemsApplication.CountAllNeedExecuteTask();int totalPagelocks (countlocks 500 - 1) / 500;//分批次处理for (int curentpage …...

Vue3+Element-plus+setup使用vuemap/vue-amap实现高德地图API相关操作
首先要下载依赖并且引入 npm安装 // 安装核心库 npm install vuemap/vue-amap --save// 安装loca库 npm install vuemap/vue-amap-loca --save// 安装扩展库 npm install vuemap/vue-amap-extra --save cdn <script src"https://cdn.jsdelivr.net/npm/vuemap/vue-a…...
Windows配置开机直达桌面并跳过锁屏登录界面在 Windows 10 中添加在启动时自动运行的应用
目录 Win10开机直达桌面并跳过锁屏登录界面修改组策略修改注册表跳过登录界面 在 Windows 10 中添加在启动时自动运行的应用设置系统级别服务一、Windows下使用sc将应用程序设置为系统服务1. 什么是sc命令?2. sc命令的基本语法3. 创建Windows服务的步骤与示例创建服…...
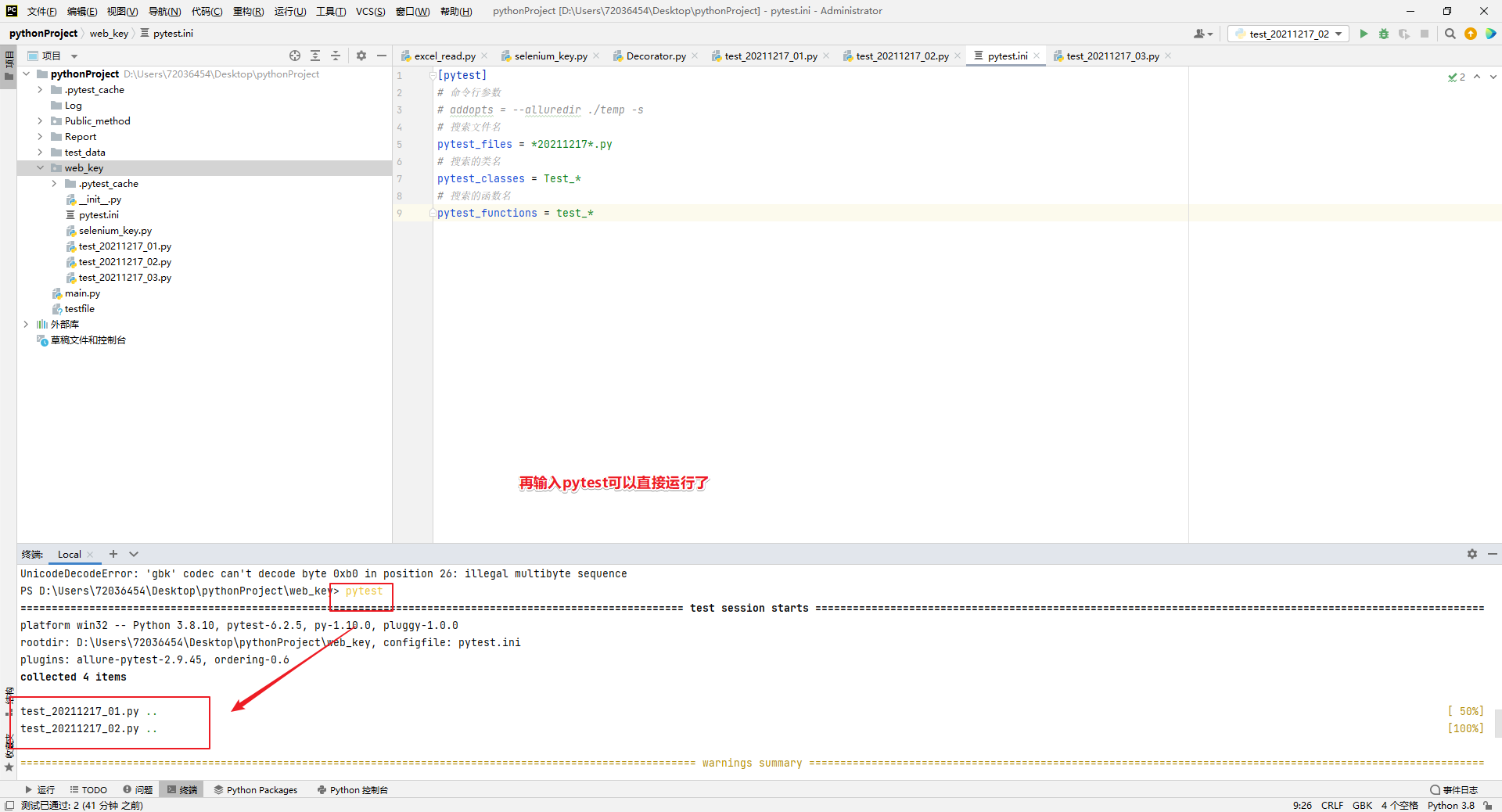
pythonUI自动化007::pytest的组成以及运行
pytest组成: 测试模块:以“test”开头或结尾的py文件 测试用例:在测试模块里或测试类里,名称符合test_xxx函数或者示例函数。 测试类:测试模块里面命名符合Test_xxx的类 函数级: import pytestclass Test…...

开放式耳机哪个品牌好用又实惠?五大口碑精品分享
如今开放式耳机市场日益火爆,不少知名品牌都在对产品进行升级迭代,那么如何在一众品牌型号中选择到自己最满意的那一款呢?开放式耳机哪个品牌好用又实惠?这就需要更专业的选购攻略,因此笔者专门整理出了专业机构的开放…...
代码随想录算法训练营day39||动态规划07:多重背包+打家劫舍
多重背包理论 描述: 有N种物品和一个容量为V 的背包。 第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。 求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。 本质: …...

WebSocket革新:用PHP实现实时Web通信
标题:WebSocket革新:用PHP实现实时Web通信 在现代Web应用中,实时通信是一个不可或缺的功能。WebSocket作为一种在单个TCP连接上进行全双工通信的协议,它允许服务器主动向客户端推送数据,极大地简化了客户端和服务器之…...

Python教程(十三):常用内置模块详解
目录 专栏列表1. os 模块2. sys 模块3. re 模块4. json 模块5. datetime 模块6. math 模块7. random 模块8. collections 模块9. itertools 模块10. threading 模块11. 加密 模块 总结 专栏列表 Python教程(十):面向对象编程(OOP…...

Linux 下的进程状态
文章目录 一、运行状态运行队列运行状态和运行队列 二、睡眠状态S状态D状态D状态产生的原因 三、暂停状态T状态t 状态 四、僵尸状态为什么有僵尸状态孤儿进程 一、运行状态 R状态:进程已经准备好随时被调度了。 运行队列 每个 CPU 都会维护一个自己的运行队列&am…...

【设计模式】六大基本原则
文章目录 开闭原则里氏替换原则依赖倒置原则单一职责原则接口隔离原则迪米特原则总结 开闭原则 核心就一句话:对扩展开放,对修改关闭。 针对的目标可以是语言层面的类、接口、方法,也可以是系统层面的功能、模块。当需求有变化的时候&#…...

Selenium网页的滚动
网页滚动功能实现 网页的滚动 如果需要对网页进行滑动操作,可以借助浏览器对象调用execute_script()方法来执行js语句,从而实现网页中的滚动下滑操作。 使用js语法实现网页滚动: # 根据x轴和y轴的值来定向滚动对应数值的距离 window.scrol…...

图算法系列1: 图算法的分类有哪些?(上)
大约在公元9世纪上半叶,来自中亚古国花剌子模的波斯数学家花剌子米(al-Khwarizmi)先后出版了两本对数学界有深远影响的书籍《印度数字算术》与《代数学》,前者在12世纪被翻译为拉丁文传入欧洲,十进制也因此传入欧洲,最终所形成的…...
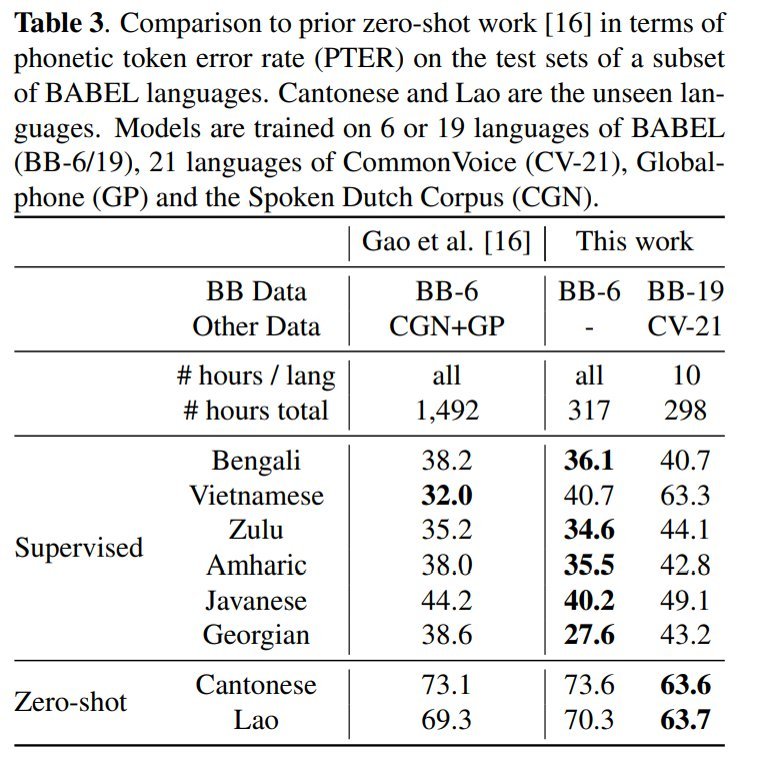
零样本学习——从多语言语料库数据中对未学习语言进行语音识别的创新技术
引言 在全球众多的语言中,只有极少数的语言在语音识别领域取得了显著的进展。这种不平衡现象的主要原因是,现有的语音识别模型往往依赖于大量的标注语音数据,而这些数据对于许多语言来说难以获得。 近年来,尽管语音识别技术取得…...

ViewStub的原理
**ViewStub是Android开发中的一个轻量级控件,主要用于懒加载布局以提高应用程序的性能和响应速度。**其原理和工作方式如下: 定义与特点 轻量级与不可见:ViewStub是一个不可见的、不占布局位置的轻量级View,它在初始化时不会实例…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
