【算法】手把手学会二分查找
目录
简介
基本步骤
第一种二分
第二种二分
例题
搜索插入位置
数的范围
总结
简介
🥥二分查找,又叫折半查找,通过找到数据二段性每次都能将原来的数据筛选掉一半,通过这个算法我们能够将一个一个查找的 O(n) 的时间复杂度优化到 O(logn) ,极大地提升了查找的效率。但使用二分进行查找必须要有一个前提,那就是查找的区间必须是有序的。如数组并非有序,则找不到该数组的的二段性。下面一起看看二分的基本步骤吧。
基本步骤
- 找一个区间 [L , R],使答案一定在该区间中。
- 找一个判断条件,使得该判断条件具有二段性,并且答案一定是该二段性的分界点。
- 分析中点 mid 在该判断条件下是否成立,如果成立,考虑答案在哪个区间,如果不成立,答案在哪个区间。
- 如果更新方式为 R = mid, 则不做处理,若更新方式是L = mid,在计算 mid 时需要 +1。
第一种二分
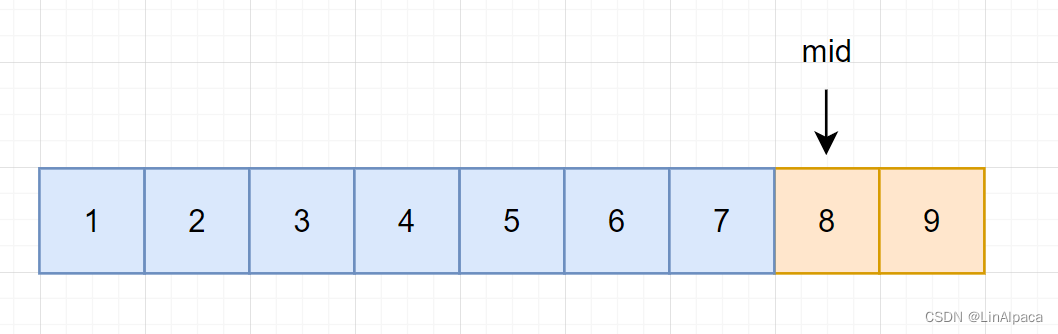
🥥假设当前我们有一个 1~9 的有序数组,现在我们要查找数组中的7。由此我们可以通过数字的大小将其分为小于 7 和 大于等于 7 的两个部分。

🥥若算出来 mid 在左区间,由于其左边的值都是小于 7 的所以不需要保留,便可以将迭代区间缩短至 [mid+1,R] 。
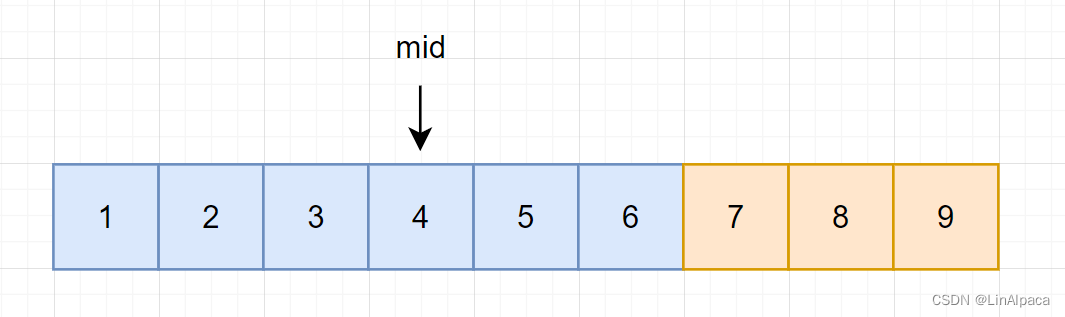
🥥而如果 mid 在右区间,这个区间的范围是大于等于 7 的,当前的值是有可能等于 7 的。
🥥所以需要将当前 mid 位保留,所以递增区间便保留至[L , mid]。
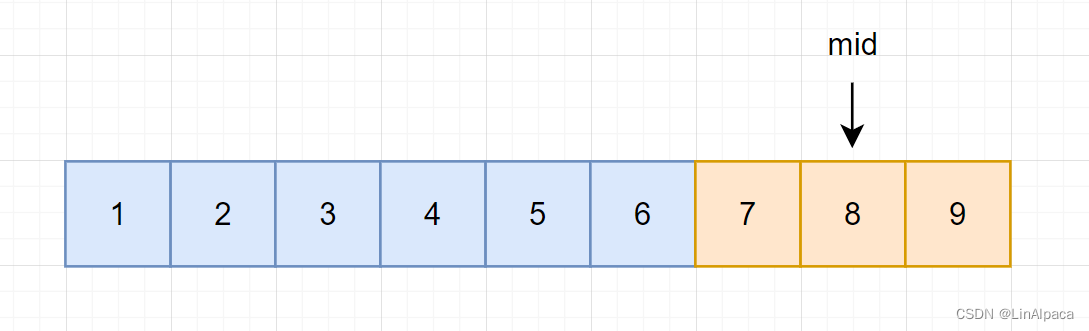
🥥并且根据上面的基本步骤的最后一步,因为更新方式为 R = mid , 则计算mid的时候不做处理。因此 mid = (L+R) / 2 。
int main()
{int arr[] = { 1,2,3,4,5,6,7,8,9 };int l = 0, r = 8,num = 7;while (l < r){int mid = (l + r) / 2; //迭代midif (arr[mid] >= num) //mid在右区间{r = mid;}else //mid在左区间{l = mid + 1;}}printf("%d\n", r); //最后l和r一定相等return 0;
}第二种二分
🥥与上面那种不一样,这次我们将原数组分作小于等于7,以及大于7的两部分。
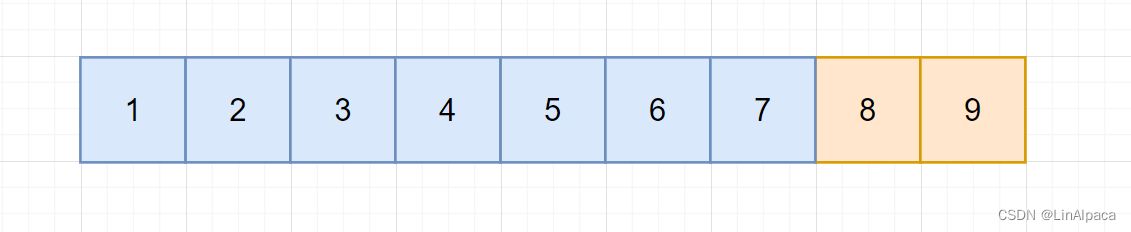
🥥且这次若 mid 在左区间,由于该区间都是小于等于目标值的,因此该部分的数据需要保留,由此迭代区间至 [mid, R] 。
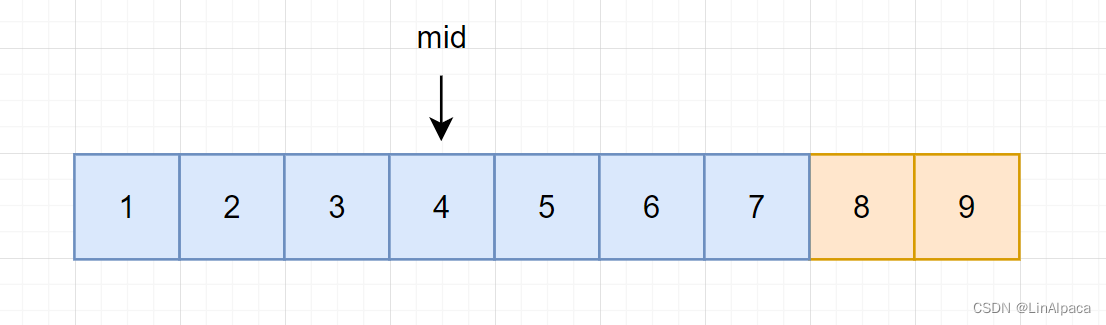
🥥而当 mid 在右区间时,由于右区间并没有我们所需要的值,所以可以不用保留,所以迭代区间至 [L,mid-1] 。
🥥而现在,由于我们使用 L = mid 进行区间的更新,因此在计算 mid 的时候还需要加上1。
int main()
{int arr[] = { 1,2,3,4,5,6,7,8,9 };int l = 0, r = 8,num = 7;while (l < r){int mid = (l + r + 1) / 2; //计算mid时要+1if (arr[mid] <= num) //mid在左区间{l = mid; //区间缩至[mid,r]}else //mid在右区间{r = mid - 1; //区间缩至[l,mid-1]} }printf("%d\n", r); //最后l一定等于rreturn 0;
}🥥根据不同的二分法,二分查找有这两种不同的写法,因此在编写程序前,要先思考当前写法该如何迭代。mid 在左区间时是怎样一种情况,在右区间又是什么情况。考虑好迭代关系,最后再处理 mid 的计算就相当简单,且不容易出错了。
例题
搜索插入位置
传送门:搜索插入位置
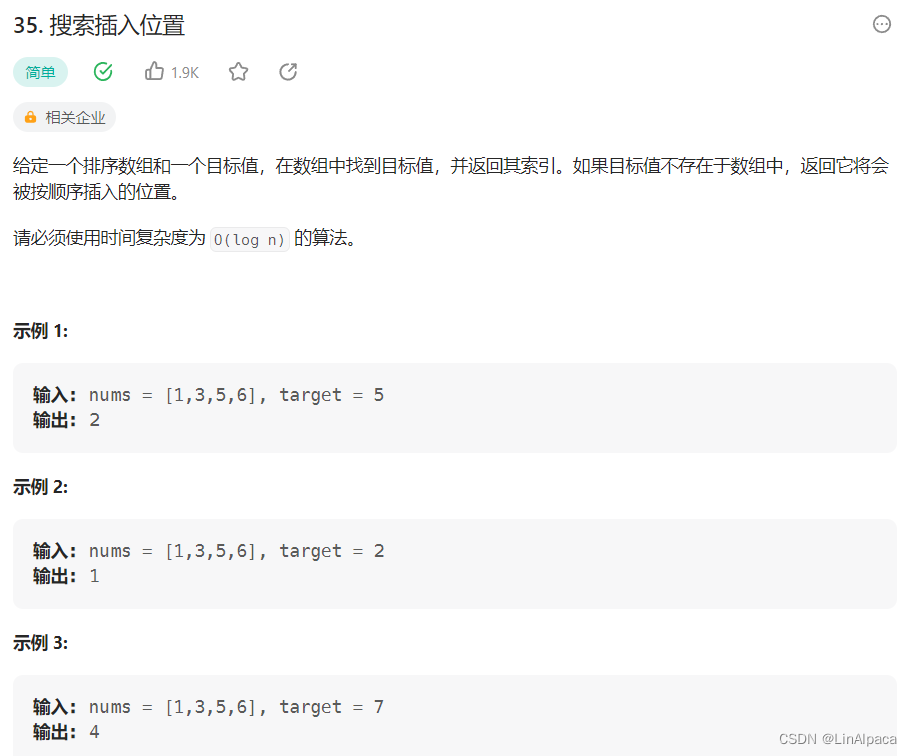
🥥这题难度相对简单,要我们在数组中找目标值,若找不到则返回目标值若插入到这个数组时的所在的下标。
🥥用我们上面的思路进行分析,我们不妨将数组分作小于目标值的以及大于等于目标值的两个区间。同时我们还要注意到目标值可能不存在或大于数组中的所有值,因此初始范围应当多扩展一位。由此便可得到代码。
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int l = 0,r = nums.size();while(l<r){int mid = (l+r)/2;if (nums[mid] >= target){r = mid;}else{l = mid + 1;}}return r;}
};数的范围
🥥传送门:AcWing 789. 数的范围

🥥通过读题我们可以知道,在这个数组之中有若干个重复的数,我们要根据题目找到一个数的区间,若无这个数则输出 -1 。但我们知道二分查找最后只能找一个数,那我们不妨这样想,因为这是个有序的数组,因此只要找到首尾两个端点就能够找到这个区间。
🥥而首尾两个点就能够用二分查找找到。分别是将数组由小于目标值和大于等于目标值、小于等于目标值和大于目标值两种分法进行划分,即进行两次二分查找,而这两次二分查找的两个分界点恰好就是一个区间的两个端点。
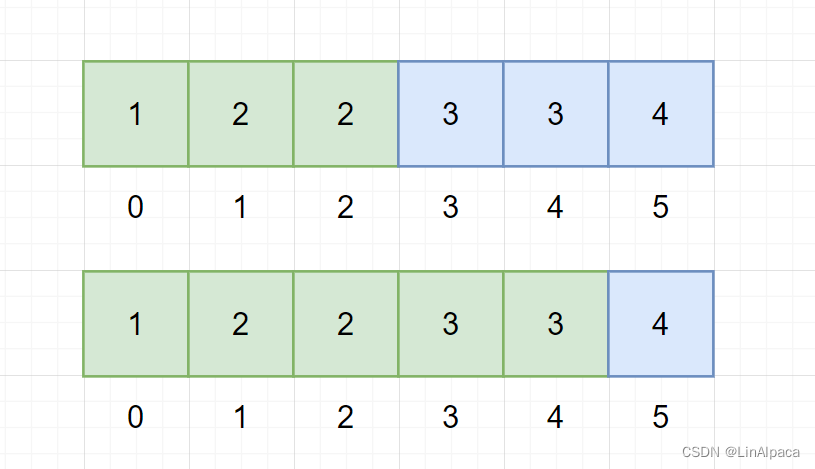
🥥即经过两次二分,分别查找左边界及右边界(若只有一个数则左右边界相等),查找一个边界后我们还可以进行一次特判,若当前端点并非我们要求的目标值,则说明这个数组之中并没有我们想要的值,因此便可以直接输出 -1 ,否则就再继续查找另一端点。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>const int N = 100000;
int n, m;
int arr[N];int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < n; i++){scanf("%d", &arr[i]);}for (int i = 0; i < m; i++) // m组数据{int num;scanf("%d", &num);//求左端点int left = 0, right = n - 1;while (left < right){int mid = (left + right) / 2;if (arr[mid] >= num){right = mid;}else{left = mid + 1;}}if (arr[left] == num){printf("%d ", left);//找右端点right = n - 1;while (left < right){int mid = (left + right + 1) / 2;if (arr[mid] <= num){left = mid;}else{right = mid - 1;}}printf("%d\n", left);}else{printf("-1 -1\n");}}return 0;
}总结
🥥二分查找的难点就在于边界的判断,因此每次在写代码前都要仔细思考,要如何进行二分?mid 在两个区间分别是什么情况?当前 mid 的值需不需要保留?最后在落实 mid 的计算。只有深刻地理解算法思想,在实际使用的时候才不会手忙脚乱。
🥥好了这次二分查找的入门讲解到这里就结束了,如果这篇文章对你有用的话还请留下你的三连加关注。
相关文章:

【算法】手把手学会二分查找
目录 简介 基本步骤 第一种二分 第二种二分 例题 搜索插入位置 数的范围 总结 简介 🥥二分查找,又叫折半查找,通过找到数据二段性每次都能将原来的数据筛选掉一半,通过这个算法我们能够将一个一个查找的 O(n) 的时间复杂…...

SVO、vinsmono、 OKVIS系统比较
几个经典视觉slam系统的比较 SVO 高翔链接:https://www.zhihu.com/question/39904950/answer/138644975处理的各个线程: tracking部分-frame to frame 、frame to map 金字塔的处理。这一步估计是从金字塔的顶层开始,把上一层的结果作为下一层估计的初…...

前端开发规范
一、开发工具 开发工具统一使用 VSCode代码格式化插件使用 Prettier代码格式校验使用 ESLintVSCode 需安装的插件有:ESLint、Prettier、Vetur 二、命名规范 项目命名使用小写字母,以连字符分隔 正确:fe-project 错误:FE PROJECT…...
不用科学上网,免费的GPT-4 IDE工具Cursor保姆级使用教程
大家好,我是可乐。 过去的一周,真是疯狂的一周。 GPT-4 震撼发布,拥有了多模态能力,不仅能和GPT3一样进行文字对话,还能读懂图片; 然后斯坦福大学发布 Alpaca 7 B,性能匹敌 GPT-3.5ÿ…...

【艾特淘】抖音小店物流体验分提升的6个维度,新手做店必看
抖音小店体验分,考核的内容包括商品、物流以及服务。大部分人会把重心放在商品评价和服务上,忽略了物流体验。但其实,抖音小店物流体验占比有20%,比服务分的占比还高一点。如果你的订单物流出了问题,很有可能会导致用户…...

数据结构——二叉树与堆
作者:几冬雪来 时间: 内容:二叉树与堆内容讲解 目录 前言: 1.完全二叉树的存储: 2.堆的实现: 1.创建文件: 2.定义结构体: 3.初始化结构体: 4.扩容空间与扩容…...
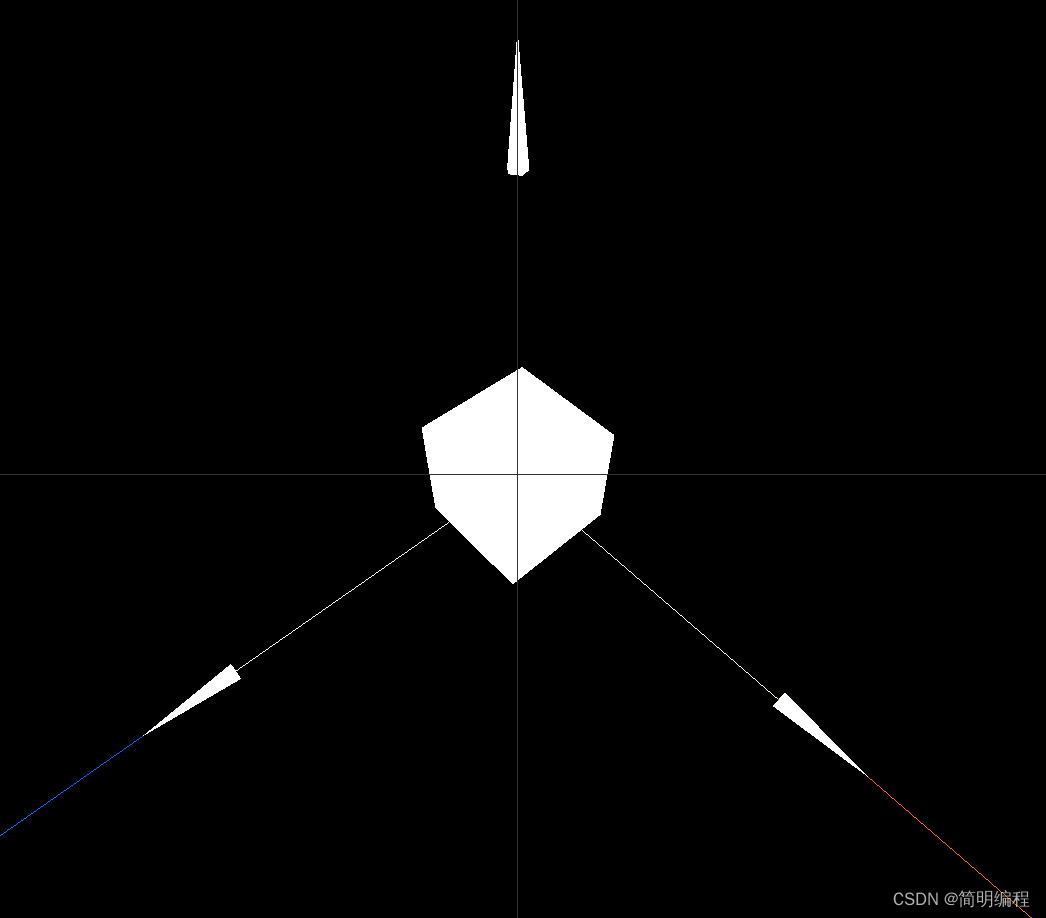
Three.js——learn02
Three.js——learn02Three.js——learn02通过轨道控制器查看物体OrbitControls核心代码index2.htmlindex.cssindex2.jsresult添加辅助器1.坐标轴辅助器AxesHelper核心代码完整代码2.箭头辅助器ArrowHelper核心代码完整代码3.相机视锥体辅助器CameraHelper核心代码完整代码Three…...

零基础小白如何入门网络安全?
我经常会看到这一类的问题: 学习XXX知识没效果; 学习XXX技能没方向; 学习XXX没办法入门; 给大家一个忠告,如果你完全没有基础的话,前期最好不要盲目去找资料学习,因为大部分人把资料收集好之…...
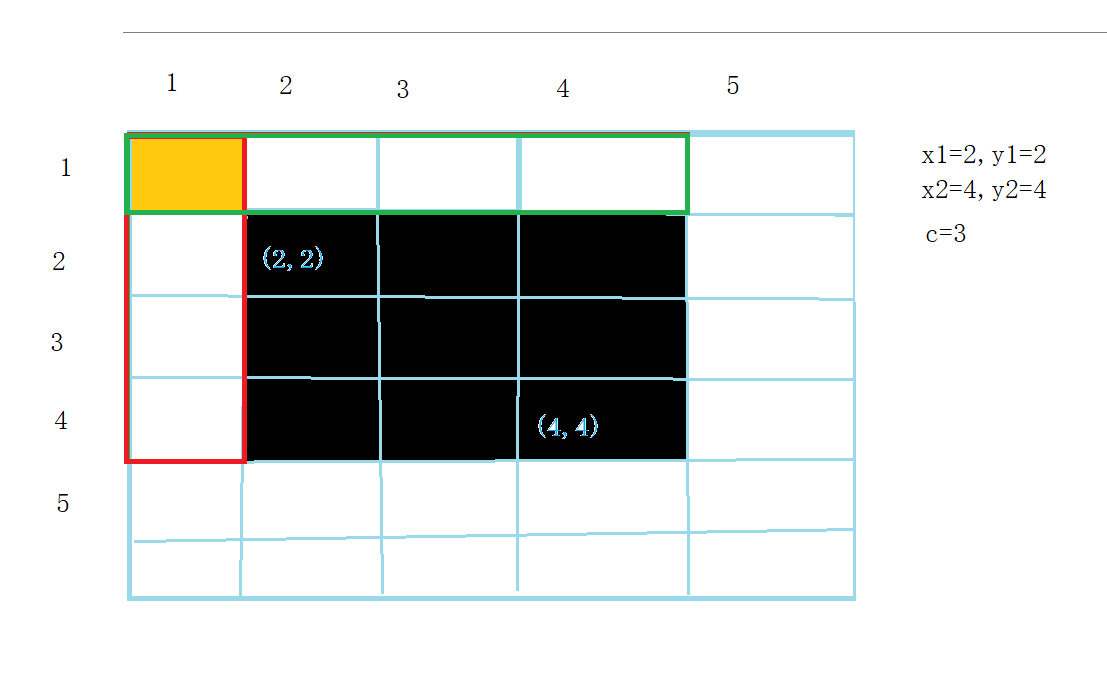
【前缀和】
前缀和前缀和子矩阵的和结语前缀和 输入一个长度为 n的整数序列。 接下来再输入 m 个询问,每个询问输入一对 l,r 对于每个询问,输出原序列中从第 l 个数到第 r个数的和。 输入格式第一行包含两个整数 n和 m 第二行包含 n个整数,表示整数…...
ChatGPT可以做WebRTC音视频质量性能优化,惊艳到我了
摘要 随着GPT-4的发布,AI的风越吹越旺。GPT-4可以回答问题,可以写作,甚至可以基于一张草图生成html代码搭建一个网站。即构社区的一位开发者倪同学就基于目前在研究的WebRTC QOS技术点对GPT-3.5跟GPT-4进行一场实验,ChatGPT会取代…...

MySQL数据库实现主从同步
安装MySQL数据库8.0.32 前言 今天来学习数据库主从同步的原理及过程,数据库主要是用来存储WEB数据,在企业当中是极为重要的,下面一起来看下。 1.1 数据库做主从的目的 MySQL主从复制在中小企业,大型企业中广泛使用,…...

go语言gin框架学习
让框架去做http解包封包等,让我们的精力用在应用层开发 MVC模式 M: model,操作数据库gorm view 视图 处理模板页面 contoller 控制器 路由 逻辑函数 解决gin相关代码飘红的问题 记得启用gomodule go env -w GO111MODULEon然后到相应目录下执行 go mod i…...

Java奠基】Java经典案例讲解
目录 卖飞机票 找质数 开发验证码 数组元素的复制 评委打分 数字加密 数字解密 抢红包 模拟双色球 二维数组 卖飞机票 需求:机票价格按照淡季旺季、头等舱和经济舱收费、输入机票原价、月份和头等舱或经济舱。按照如下规则计算机票价格: 旺季&…...

新闻文本分类任务:使用Transformer实现
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...

如何在 Vue 中使用 防抖 和 节流
大厂面试题分享 面试题库前后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库 https://mp.weixin.qq.com/s?__bizMzU5NzA0NzQyNg&mid2247485824&idx3&sn70cd26a7c0c683de64802f6cb9835003&scene21#wech…...

美国Linux服务器系统增强安全的配置
美国Linux服务器系统可能出现的安全漏洞中,更多是由于不当的系统配置所造成的,用户们可以通过一些适当的安全配置来防止问题的发生。美国Linux服务器系统上运行的服务越多,不当配置的概率也就越高,那么系统出现安全问题的可能性也…...

【史上最全面esp32教程】oled显示篇
文章目录前言介绍及库下载基础使用引脚的连接使用函数总结前言 本节课主要讲的是OLED的基础使用。使用的oled为0.96寸,128*64。 大家的其他型号也是可以用的。 提示:以下是本篇文章正文内容,下面案例可供参考 介绍及库下载 oled的简介&…...
第十四届蓝桥杯三月真题刷题训练——第 21 天
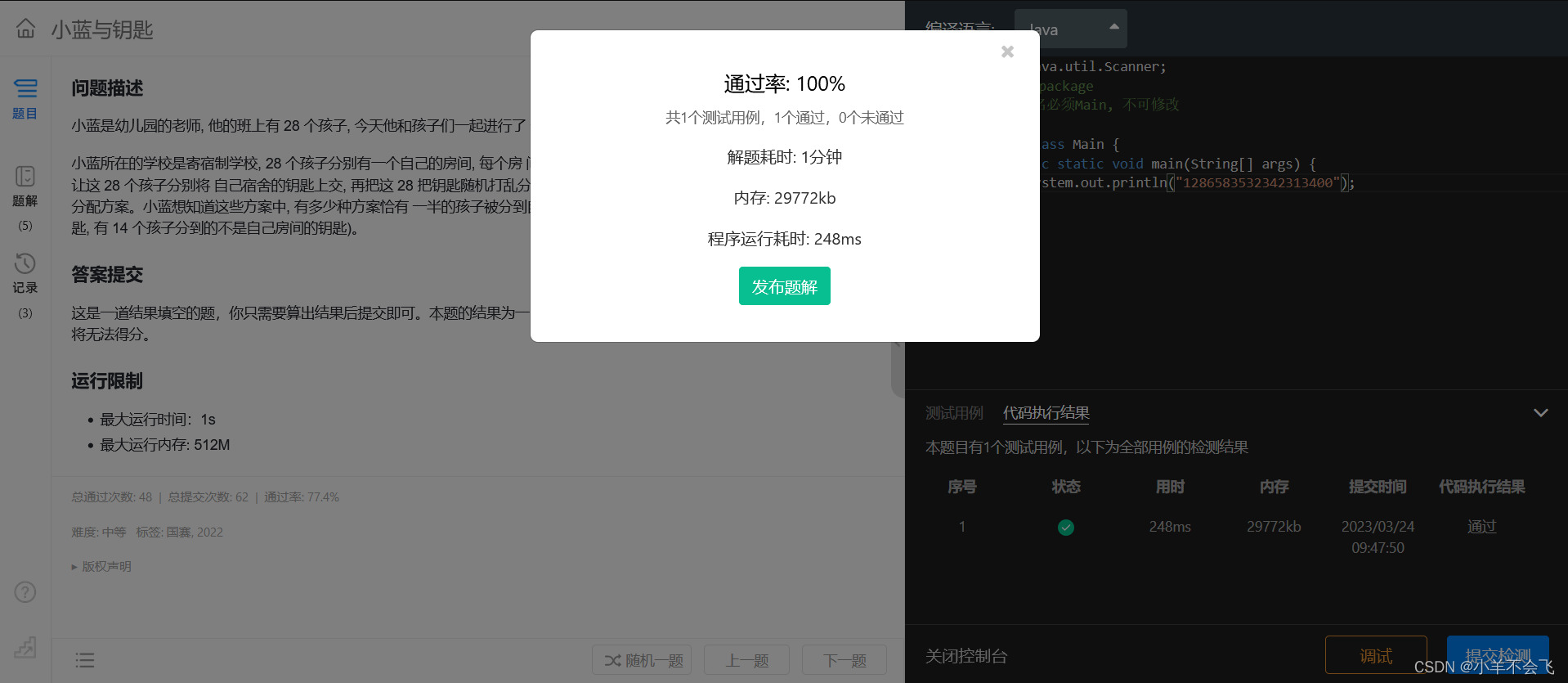
目录 第 1 题:灭鼠先锋 问题描述 运行限制 代码: 思路: 第 2 题:小蓝与钥匙 问题描述 答案提交 运行限制 代码: 思路 : 第 3 题:李白打酒加强版 第 4 题:机房 第 1 题࿱…...

css绘制一个Pinia小菠萝
效果如下: pinia小菠萝分为头部和身体,头部三片叶子,菠萝为身体 头部 先绘制头部的盒子,将三片叶子至于头部盒子中 先绘制中间的叶子,利用border-radius实现叶子的效果,可以借助工具来快速实现圆角的预想…...
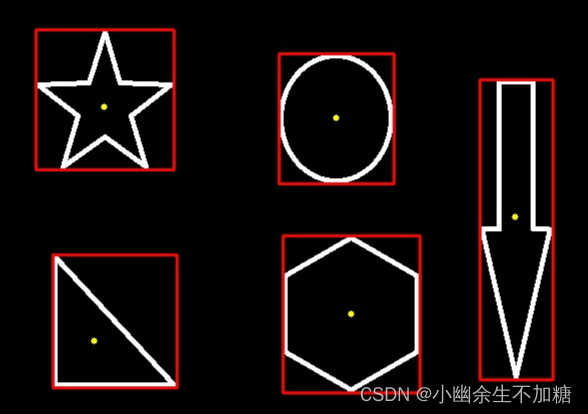
OpenCV入门(二十)快速学会OpenCV 19 对象测量
OpenCV入门(二十)快速学会OpenCV 19 对象测量1.对象测量2.多边形拟合3.计算对象中心作者:Xiou 1.对象测量 opencv 中对象测量包括: 如面积,周长,质心,边界框等。 弧长与面积测量; …...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
