【数据结构】二叉树(一)
目录
1. 树型结构
概念
树的表示形式
编辑
2. 二叉树(重点)
2.1 概念
2.2 二叉树的性质
2.3 二叉树的存储
2.4 二叉树的遍历
前中后序遍历
层序遍历:
2.5二叉树的基本操作
本篇主要理解树和二叉树相关概念,二叉树遍历及基本操作。
1. 树型结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 有一个特殊的结点,称为根结点,根结点没有前驱结点。
- 除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 树是由递归定义的。


树与非树的区分点:
- 树形结构中,子树之间不能有交集,否则就不是树形结构
- 树形结构中,除根结点外,每个节点有且仅有一个父节点,否则就不是树形结构
- 树形结构中,一颗N个结点的树有N-1条边,否则就不是树形结构
1.1概念
树型结构里,有非常多的概念,多用用就记住了

1.2树的表示形式
class Node {int value ; // 树中存储的数据Node firstChild ; // 第一个孩子引用Node nextBrother ; // 下一个兄弟引用}
结构图
2. 二叉树(重点)
2.1 概念
- 或者为空
- 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

- 空树
- 只有根节点
- 只有左子树
- 只有右子树
- 左右子树均在
两种特殊的二叉树

2.2 二叉树的性质
则对于 序号为 i 的结点有 :若 i>0 , 双亲序号: (i-1)/2 ; i=0 , i 为根结点编号 ,无双亲结点若 2i+1<n ,左孩子序号: 2i+1 ,否则无左孩子若 2i+2<n ,右孩子序号: 2i+2
相关习题,练练手吧~
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )A 不存在这样的二叉树B 200C 198D 1992. 在具有 2n 个结点的完全二叉树中,叶子结点个数为( )A nB n+1C n-1D n/23. 一个具有 767 个节点的完全二叉树,其叶子节点个数为()A 383B 384C 385D 3864. 一棵完全二叉树的节点数为 531 个,那么这棵树的高度为( )A 11B 10C 8D 12
2.3 二叉树的存储
// 孩子表示法class Node {int val ; // 数据域Node left ; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right ; // 右孩子的引用,常常代表右孩子为根的整棵右子树}// 孩子双亲表示法class Node {int val ; // 数据域Node left ; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right ; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent ; // 当前节点的根节点}
(本文采用孩子表示法)
并且二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
2.4 二叉树的遍历
前中后序遍历
public void createBinaryTree(){BTNode node1 = new BTNode(1);BTNode node1 = new BTNode(2);BTNode node1 = new BTNode(3);BTNode node1 = new BTNode(4);BTNode node1 = new BTNode(5);BTNode node1 = new BTNode(6);root = node1;node1.left = node2;node2.left = node3;node1.right = node4;node4.left = node5;node5.right = node6; }
- NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
- LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
- LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
层序遍历:
1. 某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为 ( )A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA2. 二叉树的先序遍历和中序遍历如下:先序遍历: EFHIGJK; 中序遍历: HFIEJKG. 则二叉树 根结点为 ()A: E B: F C: G D: H3.设一课二叉树的中序遍历序列: badce ,后序遍历序列: bdeca ,则二叉树前序遍历序列为 ()A: adbce B: decab C: debac D: abcde4. 某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出 ( 同一层从左到右 ) 的序列为 ()A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
2.5二叉树的基本操作
对于二叉树有以下常见操作,会在二叉树下篇经典面试题中讲解。
// 获取树中节点的个数int size ( Node root );// 获取叶子节点的个数int getLeafNodeCount ( Node root );// 子问题思路 - 求叶子结点个数// 获取第 K 层节点的个数int getKLevelNodeCount ( Node root , int k );// 获取二叉树的高度int getHeight ( Node root );// 检测值为 value 的元素是否存在Node find ( Node root , int val );// 层序遍历void levelOrder ( Node root );// 判断一棵树是不是完全二叉树boolean isCompleteTree ( Node root );
初始二叉树就到这里啦,刚了解二叉树概念性东西比较多,多看几遍就记住了。关注我,下篇讲解二叉树的多种遍历方式及多道经典面试题。不要错过喔
相关文章:
【数据结构】二叉树(一)
目录 1. 树型结构 概念 树的表示形式 编辑 2. 二叉树(重点) 2.1 概念 2.2 二叉树的性质 2.3 二叉树的存储 2.4 二叉树的遍历 前中后序遍历 层序遍历: 2.5二叉树的基本操作 本篇主要理解树和二叉树相关概念,二叉树遍…...

使用duplicate搭建备库或者级联备库
使用duplicate搭建备库或者级联备库: 主库或者源端: 1. 创建pfile,更改&添加部分参数、传输到备库; 2. 主库(或者源端)的tnsnames.ora文件添加 备库的连接信息 备库: 1. 备库添加静态监听 2…...

【存储学习笔记】4:快照(Snapshot)技术的实现方式
1 快照 1.1 动机 在上一篇《备份》里提到,热备份就是在执行操作时,服务器需要正常处理来自用户或应用对数据的更新,这样能够保证数据7*24小时可用(在很多服务里这是必要的)。 而热备份的困难就是如何保证数据的一致…...
)
数根(字符串数根公式)
公式:a的数根(a-1)%91; #include <bits/stdc.h> using namespace std; string s; long long sum; int main(){cin>>s;for(int i0;i<s.size();i){sums[i]-0;}cout<<(sum-1)%91; }...

C语言之文件操作上卷(二十一)(逆行人生-2024)
📣📣📣📣📣📣📣📣 ✏️作者主页:枫霜剑客 📋 系列专栏:C语言知识学习归纳总结(逐梦篇专栏合集) 🌲上一篇: C语…...

【微服务架构实战】结合实际案例进行微服务架构的设计与实现
微服务架构实战 结合实际案例进行微服务架构的设计与实现 引言 微服务架构(Microservices Architecture)是一种将大型应用程序拆分成一组小型、独立的服务的方法,每个服务都专注于特定的业务功能,并能够独立开发、部署和扩展。这…...

为什么要有二级指针
提示:文章 文章目录 前言一、背景二、 2.1 2.2 总结 前言 前期疑问: 本文目标: 一、背景 之前一直疑问为什么要有二级指针,一直没有写这个帖子,今天整理了一下,收获颇丰 二、 2.1 // 增加对二级指针…...

如何保证数据不丢失?(死信队列)
死信队列 1、什么是死信 死信通常是消息在特定的场景下表现: 消息被拒绝访问消费者发生异常,超过重试次数消息的Expiration过期时长或者队列TTL过期时间消息队列到达最大容量 maxLength 2、什么是死信队列 只由死信构成的消息队列是死信队列 死信队…...

树莓派开发笔记01-树莓派的系统烧录以及初次开机配置
github主页:https://github.com/snqx-lqh gitee主页:https://gitee.com/snqx-lqh 本项目github地址:https://github.com/snqx-lqh/RaspberryPiLearningNotes 本项目gitee地址:https://gitee.com/snqx-lqh/RaspberryPiLearningNote…...

微信答题小程序产品研发-后端开发
在开发答题小程序的后端服务和数据库设计时,需要考虑API的设计、数据库模型的构建以及数据的安全性和一致性。 这里我采用了云开发,后端语言是Node,数据库是NoSql,然后我简单整理了各个功能模块的后端开发概要和数据库设计。 1. …...

回溯算法——LeetCode37 解数独
题目 力扣题目链接 思路 卡哥的思路,注意看他解释为什么是“二维回溯”。我的思路,类似y总解决 N 皇后问题时的第二种方法,即从左上到右下枚举棋盘的每个位置。 至于为什么与 N 皇后问题不一样,我认为是因为它每一行不止放一个…...

【CPP】继承语法详解与菱形继承
关于我: 睡觉待开机:个人主页 个人专栏: 《优选算法》《C语言》《CPP》 生活的理想,就是为了理想的生活! 作者留言 PDF版免费提供:倘若有需要,想拿我写的博客进行学习和交流,可以私信我将免费提供PDF版。…...

数据结构(6.2_1)——领接矩阵法
图的存储——邻接矩阵法 邻接矩阵(Adjacency Matrix)是一种使用二维数组来表示图的方法。在这种表示法中,矩阵的行和列都对应图的顶点。 特点 对于无向图,如果顶点i与顶点j之间有边,则矩阵的第i行第j列(…...

诈骗未成功是否构成犯罪?
诈骗未成功不一定构成犯罪。在刑法上,构成诈骗罪需要满足特定的构成要件,包括有非法占有的目的、实施了虚构事实或隐瞒真相的行为、对方因此陷入错误认识并处分财产、行为人或第三方取得财产、被害人遭受财产损失。如果诈骗行为未能成功,即被…...
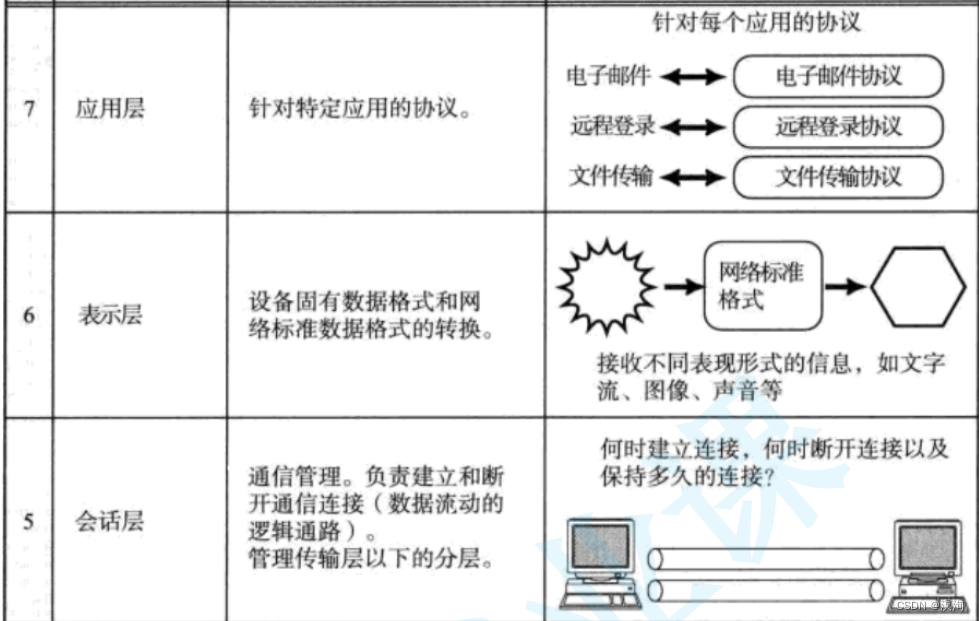
网络协议栈应用层的意义(内含思维导图和解析图通俗易懂超易理解)
绪论: “节省时间的方法就是全力以赴的将所要做的事情完美快速的做完,不留返工重新学习的时间,才能省下时间给其他你认为重要的东西。” 本章主要讲到OSI网络协议栈中的应用层的作用和再次在应用层的角度理解协议的具体意义,以及…...

【NXP-MCXA153】i2c驱动移植
介绍 I2C总线由飞利浦公司开发,是一种串行单工通信总线,它主要用于连接微控制器和其他外围设备并在总线上的器件之间传送信息(需要指定设备地址);常见的i2c设备有EEPROM、触摸屏、各种IoT传感器、时钟模块等&#x…...

C++(11)类语法分析(2)
C(10)之类语法分析(2) Author: Once Day Date: 2024年8月17日 一位热衷于Linux学习和开发的菜鸟,试图谱写一场冒险之旅,也许终点只是一场白日梦… 漫漫长路,有人对你微笑过嘛… 全系列文章可参考专栏: 源码分析_Once-Day的博客-CSDN博客 …...
)
数字验证每日十问--(3)
深拷贝和浅拷贝的区别? 当只拷贝对象中的成员变量和声明的句柄时,称为浅拷贝。浅拷贝只把对象中的句柄复制了,却没有复制句柄b所指向的对象。这会导致复制后,a2中的句柄b 和 a1 中的句柄b指向同一个对象,如果a2中的句…...

22.给定 n 对括号,实现一个算法生成所有可能的正确匹配的括号组合
22. Generate Parentheses 题目 给定 n 对括号,编写一个函数生成所有可能的正确匹配的括号组合。 例如,当 n = 3 时,可能的组合集合为: ["((()))","(()())","(())()","()(())","()()()" ]题目大意 给出 n 代表生成…...

检测到目标URL存在http host头攻击漏洞
漏洞描述 修复措施 方法一: nginx 的 default_server 指令可以定义默认的 server 去处理一些没有匹配到 server_name 的请求,如果没有显式定义,则会选取第一个定义的 server 作为 default_server。 server { …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

