第43课 Scratch入门篇:雪花随风飘
雪花随风飘
故事背景:
雪花轻轻地从灰蒙蒙的天空中飘落下来,它们像是天空中飘洒下来的羽毛,又像是冬日的精灵在翩翩起舞。每一片雪花都独一无二,它们在空中旋转、飘荡,最终缓缓降落在屋顶、树枝、街道和行人的肩头。

程序原理:
众多的雪花肯定是克隆功能,降落过程是通过Y 坐标的减少,而左右飘动则是利用鼠标的位置,为了避免雪花跟着鼠标,我们设置了移动距离为鼠标的 x 坐标/50,当然这个 50 不是固定的,如果大家想让雪花左右飘动距离大些,可以把数字改小,否则就是加大。
开始编程
1、使用角色上传功能,上传一个雪花的图片

2、编辑雪花程序,我们先实现最基本的雪花从最上方掉落:
- 点击绿旗的时候设定雪花在舞台的最上方(随机x的位置),Y 坐标为 180
- 雪花下落的过程,是通过 Y 坐标减少来实现的。
- 判断雪花碰到舞台的底部,则把雪花移动到舞台的最上方重新飘落。
相关文章:

第43课 Scratch入门篇:雪花随风飘
雪花随风飘 故事背景: 雪花轻轻地从灰蒙蒙的天空中飘落下来,它们像是天空中飘洒下来的羽毛,又像是冬日的精灵在翩翩起舞。每一片雪花都独一无二,它们在空中旋转、飘荡,最终缓缓降落在屋顶、树枝、街道和行人的肩头。 程序原理: 众多的雪花肯定是克隆功能,降落过程是通过…...

VueUse 基于 Vue 3 Composition API 的高质量 Hooks 库
VueUse 是什么? VueUse 是基于 Vue 3 Composition API 的高质量 Hooks 库。例如获取滚动的距离 VueUse 官网:VueUse | VueUse VueUse 什么使用? 1、通过npm安装 VueUse npm i @vueuse/core 2、搜索需要使用的函数,例如搜索 useScroll 滚动 3、使用useScroll 滚动函数 …...

ARM CoreLink 系列 5.1.1 -- CI-700 System Address Map 】
文章目录 System Address MapRN SAMRN SAM memory regions and target typesSAM memory region size configurationRN SAM target ID selectionSystem Address Map 所有的CHI 命令都包含一个 Source ID 和 Target ID, 其中 Source ID 可以来自于 RN Node, Target ID 可以来自…...
【数据结构】二叉树(一)
目录 1. 树型结构 概念 树的表示形式 编辑 2. 二叉树(重点) 2.1 概念 2.2 二叉树的性质 2.3 二叉树的存储 2.4 二叉树的遍历 前中后序遍历 层序遍历: 2.5二叉树的基本操作 本篇主要理解树和二叉树相关概念,二叉树遍…...

使用duplicate搭建备库或者级联备库
使用duplicate搭建备库或者级联备库: 主库或者源端: 1. 创建pfile,更改&添加部分参数、传输到备库; 2. 主库(或者源端)的tnsnames.ora文件添加 备库的连接信息 备库: 1. 备库添加静态监听 2…...

【存储学习笔记】4:快照(Snapshot)技术的实现方式
1 快照 1.1 动机 在上一篇《备份》里提到,热备份就是在执行操作时,服务器需要正常处理来自用户或应用对数据的更新,这样能够保证数据7*24小时可用(在很多服务里这是必要的)。 而热备份的困难就是如何保证数据的一致…...
)
数根(字符串数根公式)
公式:a的数根(a-1)%91; #include <bits/stdc.h> using namespace std; string s; long long sum; int main(){cin>>s;for(int i0;i<s.size();i){sums[i]-0;}cout<<(sum-1)%91; }...

C语言之文件操作上卷(二十一)(逆行人生-2024)
📣📣📣📣📣📣📣📣 ✏️作者主页:枫霜剑客 📋 系列专栏:C语言知识学习归纳总结(逐梦篇专栏合集) 🌲上一篇: C语…...

【微服务架构实战】结合实际案例进行微服务架构的设计与实现
微服务架构实战 结合实际案例进行微服务架构的设计与实现 引言 微服务架构(Microservices Architecture)是一种将大型应用程序拆分成一组小型、独立的服务的方法,每个服务都专注于特定的业务功能,并能够独立开发、部署和扩展。这…...

为什么要有二级指针
提示:文章 文章目录 前言一、背景二、 2.1 2.2 总结 前言 前期疑问: 本文目标: 一、背景 之前一直疑问为什么要有二级指针,一直没有写这个帖子,今天整理了一下,收获颇丰 二、 2.1 // 增加对二级指针…...

如何保证数据不丢失?(死信队列)
死信队列 1、什么是死信 死信通常是消息在特定的场景下表现: 消息被拒绝访问消费者发生异常,超过重试次数消息的Expiration过期时长或者队列TTL过期时间消息队列到达最大容量 maxLength 2、什么是死信队列 只由死信构成的消息队列是死信队列 死信队…...

树莓派开发笔记01-树莓派的系统烧录以及初次开机配置
github主页:https://github.com/snqx-lqh gitee主页:https://gitee.com/snqx-lqh 本项目github地址:https://github.com/snqx-lqh/RaspberryPiLearningNotes 本项目gitee地址:https://gitee.com/snqx-lqh/RaspberryPiLearningNote…...

微信答题小程序产品研发-后端开发
在开发答题小程序的后端服务和数据库设计时,需要考虑API的设计、数据库模型的构建以及数据的安全性和一致性。 这里我采用了云开发,后端语言是Node,数据库是NoSql,然后我简单整理了各个功能模块的后端开发概要和数据库设计。 1. …...

回溯算法——LeetCode37 解数独
题目 力扣题目链接 思路 卡哥的思路,注意看他解释为什么是“二维回溯”。我的思路,类似y总解决 N 皇后问题时的第二种方法,即从左上到右下枚举棋盘的每个位置。 至于为什么与 N 皇后问题不一样,我认为是因为它每一行不止放一个…...

【CPP】继承语法详解与菱形继承
关于我: 睡觉待开机:个人主页 个人专栏: 《优选算法》《C语言》《CPP》 生活的理想,就是为了理想的生活! 作者留言 PDF版免费提供:倘若有需要,想拿我写的博客进行学习和交流,可以私信我将免费提供PDF版。…...

数据结构(6.2_1)——领接矩阵法
图的存储——邻接矩阵法 邻接矩阵(Adjacency Matrix)是一种使用二维数组来表示图的方法。在这种表示法中,矩阵的行和列都对应图的顶点。 特点 对于无向图,如果顶点i与顶点j之间有边,则矩阵的第i行第j列(…...

诈骗未成功是否构成犯罪?
诈骗未成功不一定构成犯罪。在刑法上,构成诈骗罪需要满足特定的构成要件,包括有非法占有的目的、实施了虚构事实或隐瞒真相的行为、对方因此陷入错误认识并处分财产、行为人或第三方取得财产、被害人遭受财产损失。如果诈骗行为未能成功,即被…...
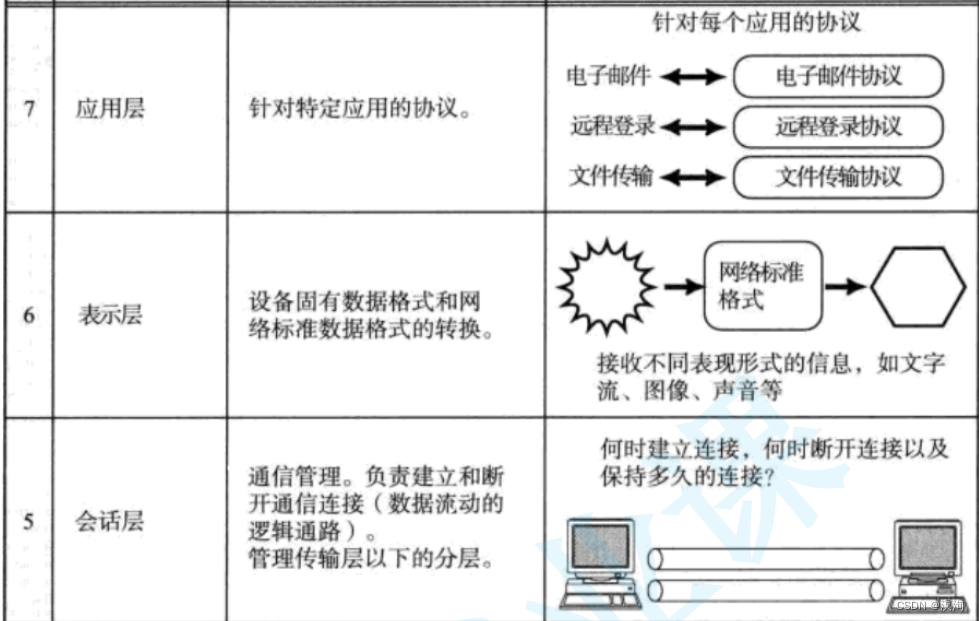
网络协议栈应用层的意义(内含思维导图和解析图通俗易懂超易理解)
绪论: “节省时间的方法就是全力以赴的将所要做的事情完美快速的做完,不留返工重新学习的时间,才能省下时间给其他你认为重要的东西。” 本章主要讲到OSI网络协议栈中的应用层的作用和再次在应用层的角度理解协议的具体意义,以及…...

【NXP-MCXA153】i2c驱动移植
介绍 I2C总线由飞利浦公司开发,是一种串行单工通信总线,它主要用于连接微控制器和其他外围设备并在总线上的器件之间传送信息(需要指定设备地址);常见的i2c设备有EEPROM、触摸屏、各种IoT传感器、时钟模块等&#x…...

C++(11)类语法分析(2)
C(10)之类语法分析(2) Author: Once Day Date: 2024年8月17日 一位热衷于Linux学习和开发的菜鸟,试图谱写一场冒险之旅,也许终点只是一场白日梦… 漫漫长路,有人对你微笑过嘛… 全系列文章可参考专栏: 源码分析_Once-Day的博客-CSDN博客 …...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
