【OCR 学习笔记】二值化——全局阈值方法
二值化——全局阈值方法
- 固定阈值方法
- Otsu算法
- 在OpenCV中的实现
- 固定阈值
- Otsu算法
图像二值化(Image Binarization)是指将像素点的灰度值设为0或255,使图像呈现明显的黑白效果。二值化一方面减少了数据维度,另一方面通过排除原图中噪声带来的干扰,可以凸显有效区域的轮廓结构。OCR效果很大程度上取决于该步骤,高质量的二值图像可以显著提升识别的准确率。目前,二值化的方法主要分为全局阈值方法(Global Binarization)、局部阈值方法(Local Binarization)、基于深度学习的方法和其他方法。
固定阈值方法
该方法对输入图像中的所有像素点统一使用同一个固定阈值。其算法如下:
g ( x , y ) = { 255 , 若 f ( x , y ) ≥ T 0 , 否则 g(x,y)=\begin{cases} 255, & 若f(x,y)\geq T \\ 0, & 否则 \end{cases} g(x,y)={255,0,若f(x,y)≥T否则
- T T T为全局阈值
不同的阈值 T T T会产生不同的二值化效果。对于不同的输入图像,最佳的阈值 T T T也不一样,这也是固定阈值方法的主要缺陷。
于是,解决这一缺陷的相应算法也随之而出现;下面的几种方法均采用了根据输入图像计算最佳阈值的思想。
Otsu算法
Ostu算法1又称最大类间方差法,由日本学者Nobuyuki Ostu于1979年提出,是一种在自适应的阈值确定方法。
Ostu算法将输入图像分为 L L L个灰度级, n i n_i ni表示灰度级为 i i i的像素个数,则像素总数 N = n 1 + n 2 + ⋯ + n L N=n_1+n_2+ \cdots +n_L N=n1+n2+⋯+nL。为了简化讨论,这里使用归一化的灰度直方图,并将其视为输入图像的概率分布:
p i = n i / N , p i > 0 , ∑ i = 1 L p i = 1 p_i=n_i/N, p_i>0, \sum_{i=1}^{L}p_i=1 pi=ni/N,pi>0,i=1∑Lpi=1
现假设在第 k k k个灰度级设置阈值,将图像分为 C 0 C_0 C0和 C 1 C_1 C1(背景和目标物体), C 0 C_0 C0表示灰度级为 [ 1 , ⋯ , k ] [1, \cdots, k] [1,⋯,k]的像素点, C 1 C_1 C1表示灰度级为 [ k + 1 , ⋯ , L ] [k+1, \cdots, L] [k+1,⋯,L]的像素点,那么两类出现的概率以及类内灰度级的均值分别为:
ω 0 = P r ( C 0 ) = ∑ i = 1 k p i = ω ( k ) ω 1 = P r ( C 1 ) = ∑ i = k + 1 L p i = 1 − ω ( k ) μ 0 = ∑ i = 1 k i P r ( i ∣ C 0 ) = ∑ i = 1 k i p i / ω 0 = μ ( k ) / ω ( k ) μ 1 = ∑ i = k + 1 L i P r ( i ∣ C 1 ) = ∑ i = k + 1 k i p i / ω 1 = μ T − μ ( k ) 1 − ω ( k ) \omega_0=Pr(C_0)=\sum_{i=1}^{k}p_i=\omega(k) \\ \omega_1=Pr(C_1)=\sum_{i=k+1}^{L}p_i=1-\omega(k) \\ \mu_0=\sum_{i=1}^{k}i Pr(i|C_0)=\sum_{i=1}^{k}ip_i/\omega_0=\mu(k)/\omega(k) \\ \mu_1=\sum_{i=k+1}^{L}i Pr(i|C_1)=\sum_{i=k+1}^{k}ip_i/\omega_1=\frac{\mu_T-\mu(k)}{1-\omega(k)} ω0=Pr(C0)=i=1∑kpi=ω(k)ω1=Pr(C1)=i=k+1∑Lpi=1−ω(k)μ0=i=1∑kiPr(i∣C0)=i=1∑kipi/ω0=μ(k)/ω(k)μ1=i=k+1∑LiPr(i∣C1)=i=k+1∑kipi/ω1=1−ω(k)μT−μ(k)
- ω ( k ) \omega(k) ω(k)和 μ ( k ) \mu(k) μ(k)分别为灰度级从1到 k k k的累计出现概率和平均灰度级;
- μ T \mu_T μT为整张图像的平均灰度级。
容易证得,对于任意 k k k值均有:
ω 0 μ 0 + ω 1 μ 1 = μ T , ω 0 + ω 1 = 1 \omega_0\mu_0+\omega_1\mu_1=\mu_T, \omega_0+\omega_1=1 ω0μ0+ω1μ1=μT,ω0+ω1=1
这两类得类内方差也可以算得:
σ 0 2 = ∑ i = 1 k ( i − μ 0 ) 2 P r ( i ∣ C 0 ) = ∑ i = 1 k ( i − μ 0 ) 2 p i / ω 0 σ 1 2 = ∑ i = k + 1 L ( i − μ 1 ) 2 P r ( i ∣ C 0 ) = ∑ i = k + 1 L ( i − μ 1 ) 2 p i / ω 1 \sigma_0^2=\sum_{i=1}^{k}(i-\mu_0)^2Pr(i|C_0)=\sum_{i=1}^{k}(i-\mu_0)^2p_i/\omega_0 \\ \sigma_1^2=\sum_{i=k+1}^{L}(i-\mu_1)^2Pr(i|C_0)=\sum_{i=k+1}^{L}(i-\mu_1)^2p_i/\omega_1 σ02=i=1∑k(i−μ0)2Pr(i∣C0)=i=1∑k(i−μ0)2pi/ω0σ12=i=k+1∑L(i−μ1)2Pr(i∣C0)=i=k+1∑L(i−μ1)2pi/ω1
为了评价阈值 k k k的好坏,需要引入判别式:
λ = σ B 2 / σ W 2 , κ = σ T 2 / σ W 2 , η = σ B 2 / σ T 2 ( 1 ) \lambda=\sigma_B^2/\sigma_W^2, \kappa=\sigma_T^2/\sigma_W^2, \eta=\sigma_B^2/\sigma_T^2 \qquad (1) λ=σB2/σW2,κ=σT2/σW2,η=σB2/σT2(1)
其中
- σ W 2 = ω 0 σ 0 2 + ω 1 σ 1 2 \sigma_W^2=\omega_0\sigma_0^2+\omega_1\sigma_1^2 σW2=ω0σ02+ω1σ12,即类内方差
- σ B 2 = ω 0 ( μ 0 − μ T ) 2 + ω ( μ 1 − μ T ) 2 = ω 0 ω 1 ( μ 1 − μ 0 ) 2 \sigma_B^2=\omega_0(\mu_0-\mu_T)^2+\omega(\mu_1-\mu_T)^2=\omega_0\omega_1(\mu_1-\mu_0)^2 σB2=ω0(μ0−μT)2+ω(μ1−μT)2=ω0ω1(μ1−μ0)2,即类间方差
- σ T 2 = ∑ i = 1 L ( i − μ T ) 2 p i \sigma_T^2=\sum_{i=1}^{L}(i-\mu_T)^2p_i σT2=∑i=1L(i−μT)2pi,即灰度级的总方差
由于 σ W 2 + σ B 2 = σ T 2 \sigma_W^2+\sigma_B^2=\sigma_T^2 σW2+σB2=σT2始终成立,而对同一张图片来说 σ T 2 \sigma_T^2 σT2是确定的,所以 σ W 2 \sigma_W^2 σW2和 σ B 2 \sigma_B^2 σB2,一个越大,另一个就会越小。这样的话,(1)式中的三个目标值 λ , κ , η \lambda, \kappa, \eta λ,κ,η就总是同向运动的。
但是从计算简单程度上来说,因为 σ T 2 \sigma_T^2 σT2与 k k k无关,且 σ B 2 \sigma_B^2 σB2只涉及均值的运算。因此, η \eta η是判别 k k k取值好坏的最简单的衡量标准:
η = σ B 2 ( k ) / σ T 2 \eta = \sigma_B^2(k)/\sigma_T^2 η=σB2(k)/σT2
因此,最佳的 k k k值选择( k ∗ k^* k∗)满足:
σ B 2 ( k ∗ ) = max 1 ≤ k ≤ L σ B 2 ( k ) \sigma_B^2(k^*)=\max_{1\leq k \leq L}\sigma_B^2(k) σB2(k∗)=1≤k≤LmaxσB2(k)
在OpenCV中的实现
固定阈值
固定阈值可以在OpenCV中用adptiveThreshold()函数来实现,其函数原型如下:
void cv::adptiveThreshold( InputArray src,OutputArray dst,double maxValue,int adaptiveMethod,int thresholdType,int blockSize,double C)
将其中的第5个参数thresholdType指定为THRESH_BINARY就是固定阈值方法。
Otsu算法
Otsu算法可以在OpenCV中用threshold()函数来实现,其函数原型如下:
double cv::threshold( InputArray src,OutputArray dst,double thresh,double maxval,int type)
将其中的第5个参数type指定为THRESH_OTSU就是Otsu算法。
这个函数也可以用来通过将该参数指定为THRESH_BINARY来使用固定阈值的方法。
以下是Otsu算法的一个结果示例(上:原图,中:直方图,下:二值化后的结果):
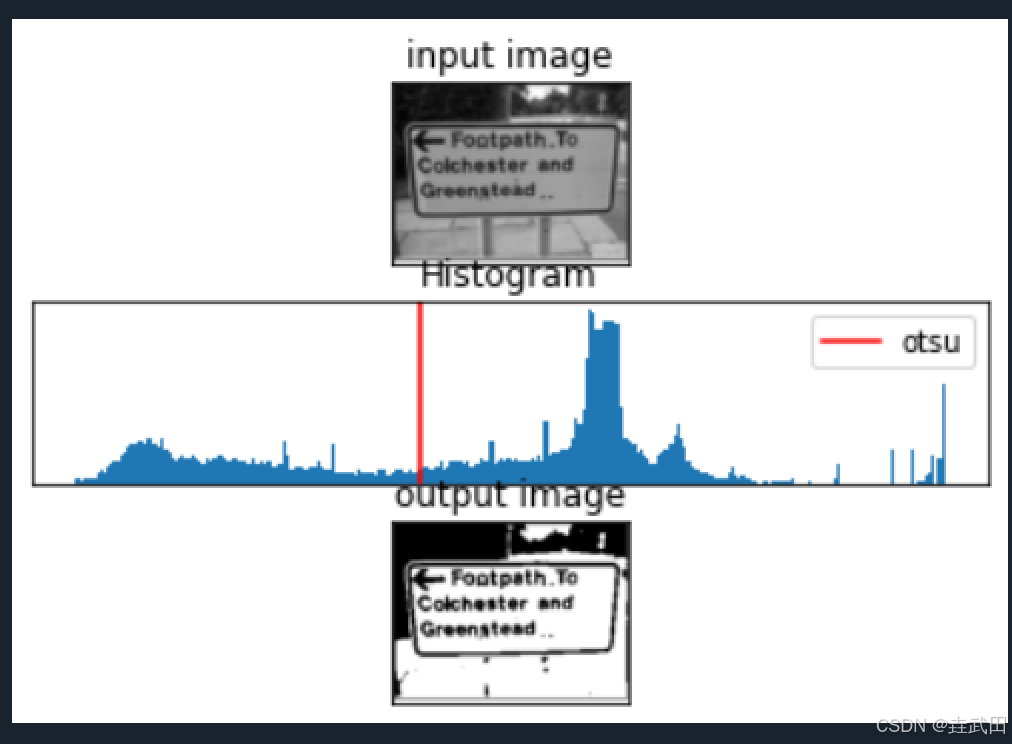
直方图中的红色竖线为Otsu算法找出的最佳阈值。
Otsu N. A Threshold Selection Method From Gray-Level Histogram. IEEE Transactions On Systems Man Cybernetics, 1979, 9(1): 62-66. ↩︎
相关文章:

【OCR 学习笔记】二值化——全局阈值方法
二值化——全局阈值方法 固定阈值方法Otsu算法在OpenCV中的实现固定阈值Otsu算法 图像二值化(Image Binarization)是指将像素点的灰度值设为0或255,使图像呈现明显的黑白效果。二值化一方面减少了数据维度,另一方面通过排除原图中…...
Java - IDEA开发
使用IDEA开发Java程序步骤: 创建工程 Project;创建模块 Module;创建包 Package;创建类;编写代码; 如何查看JDK版本 Package介绍: package是将项目中的各种文件,比如源代码、编译生成的字节码、配置文件、…...
什么是内存优化表(In-Memory Table)?)
Oracle(62)什么是内存优化表(In-Memory Table)?
内存优化表(In-Memory Table)是指将表的数据存储在内存中,以提高数据访问和查询性能的一种技术。内存优化表通过利用内存的高速访问特性,显著减少I/O操作的延迟,提升数据处理的速度。这种技术在需要高性能数据处理的应…...
#window家庭版安装hyper-v#
由于window 11 家庭版没有hyper-v虚拟机服务,则需要安装一下,使用如下操作 1:新建一个txt文件,拷贝如下脚本到里面 pushd "%\~dp0" dir /b %SystemRoot%\servicing\Packages\*Hyper-V*.mum >hyper-v.txt for /f %%i in (findst…...

【云原生】Pass容器研发基础——汇总篇
云原生基础汇总 系列综述: 💞目的:本系列是个人整理为了云计算学习的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:每个知识点的修正和深入主要参考各平台大佬的文章,…...
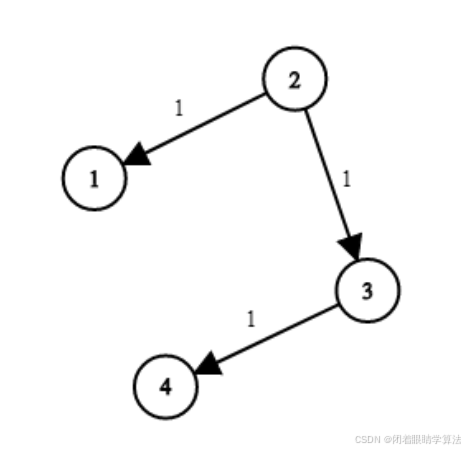
【Py/Java/C++三种语言详解】LeetCode743、网络延迟时间【单源最短路问题Djikstra算法】
可上 欧弟OJ系统 练习华子OD、大厂真题 绿色聊天软件戳 od1441了解算法冲刺训练(备注【CSDN】否则不通过) 文章目录 相关推荐阅读一、题目描述二、题目解析三、参考代码PythonJavaC 时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 相关推荐阅读 …...

交替输出
交替输出 题目:线程 1 输出 a 5 次,线程 2 输出 b 5 次,线程 3 输出 c 5 次。现在要求输出 abcabcabcabcabc wait notify 版 public class SyncWaitNotify {private volatile int flag;private volatile int loopNumber;public SyncWaitNo…...
——更改html内数据)
JS(三)——更改html内数据
获取 DOM 元素,然后修改其属性或内容。使用 getElementById 方法获取特定 ID 的元素: <p id"myParagraph">这是初始的文本</p> const paragraph document.getElementById(myParagraph); paragraph.innerHTML 这是修改后的文本…...

CSS小玩意儿:文字适配背景
一,效果 二,代码 1,搭个框架 添加一张背景图片,在图片中显示一行文字。 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" conte…...
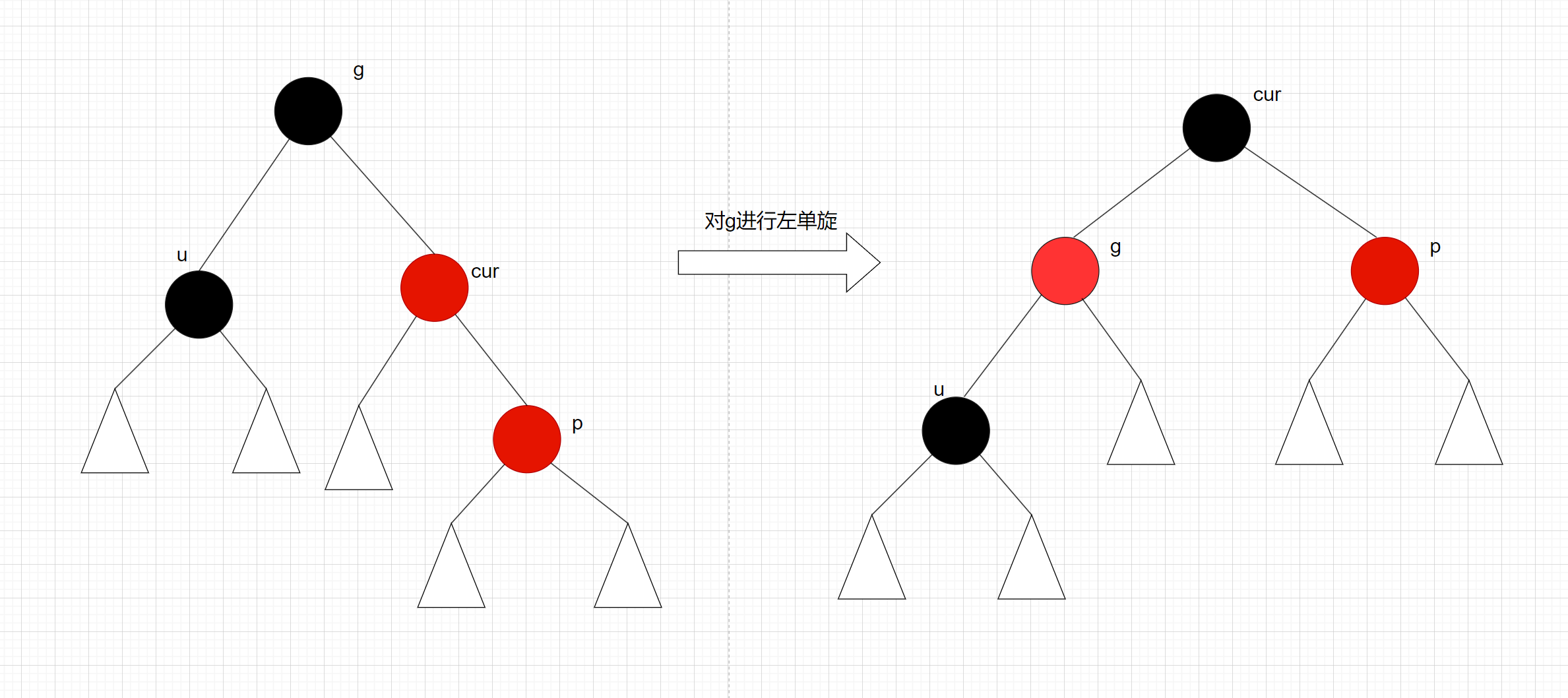
C++:平衡二叉搜索树之红黑树
一、红黑树的概念 红黑树, 和AVL都是二叉搜索树, 红黑树通过在每个节点上增加一个储存位表示节点的颜色, 可以是RED或者BLACK, 通过任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树能够确保没有一条路径会比…...

CentOS 7 系统优化
CentOS 7 系统优化 1、配置YUM源 阿里云的YUM源配置: CentOS 7使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repoCentOS 8使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS…...

扫雷游戏——附源代码
扫雷游戏的源代码比较简单,不设计比较复杂的代码,主要是多个函数的组合,每个函数执行自己的功能,最终支持游戏的完成。 1.菜单 我们需要一个提醒信息来让用户进行选择。 void menu() {printf("***********************\n&…...
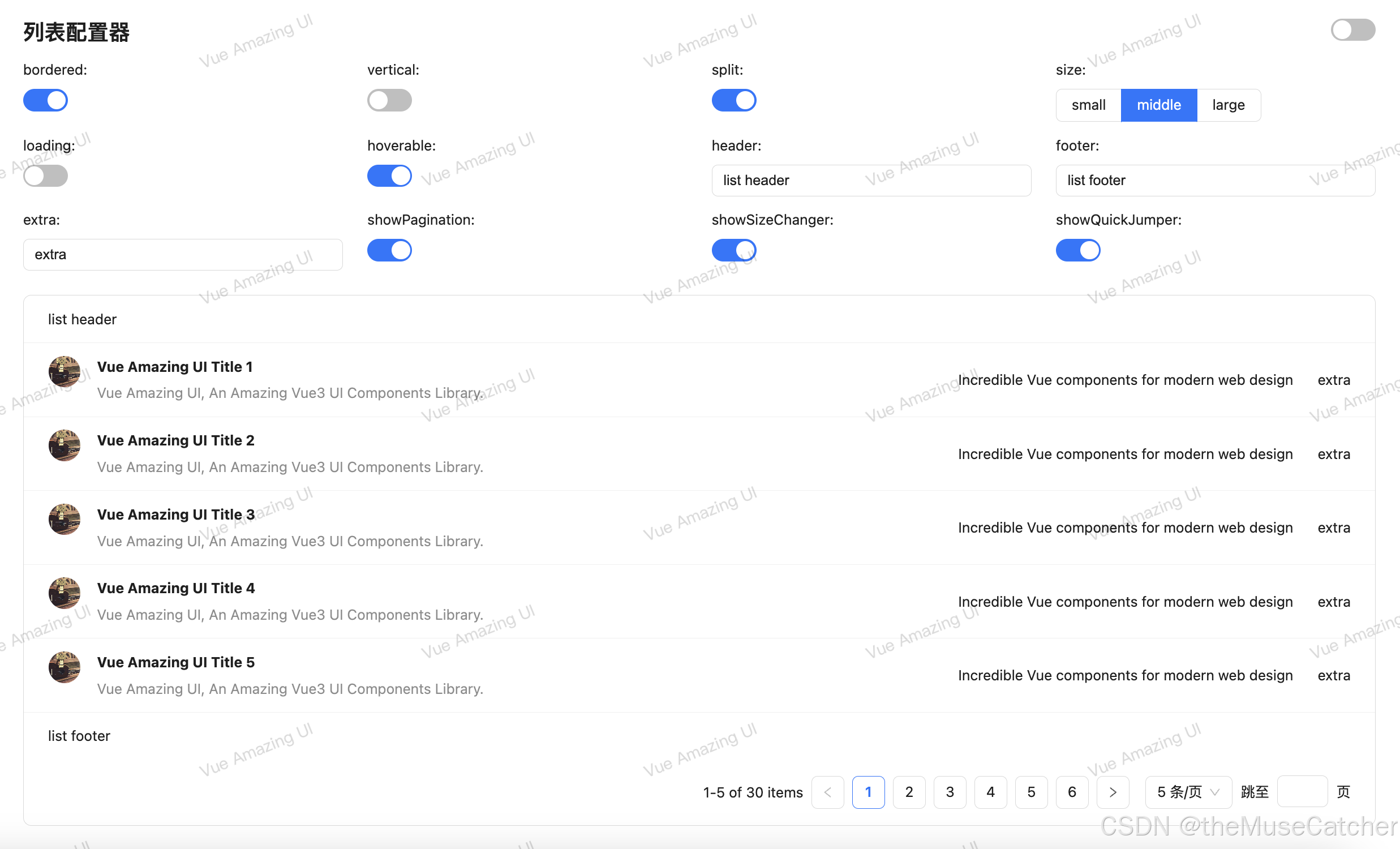
Vue3列表(List)
效果如下图:在线预览 APIs List 参数说明类型默认值bordered是否展示边框booleanfalsevertical是否使用竖直样式booleanfalsesplit是否展示分割线booleantruesize列表尺寸‘small’ | ‘middle’ | ‘large’‘middle’loading是否加载中booleanfalsehoverable是否…...

HarmonyOS NEXT - Navigation组件封装BaseNavigation
demo 地址: https://github.com/iotjin/JhHarmonyDemo 代码不定时更新,请前往github查看最新代码 在demo中这些组件和工具类都通过module实现了,具体可以参考HarmonyOS NEXT - 通过 module 模块化引用公共组件和utils 官方介绍 组件导航 (Navigation)(推…...
浅看MySQL数据库
有这么一句话:“一个不会数据库的程序员不是合格的程序员”。有点夸张,但是确是如此。透彻学习数据库是要学习好多知识,需要学的东西也是偏难的。我们今天来看数据库MySQL的一些简单基础东西,跟着小编一起来看一下吧。 什么是数据…...
)
Pytorch常用训练套路框架(CPU)
文章目录 1. 数据准备示例:加载 CIFAR-10 数据集 2. 模型定义示例:定义一个简单的卷积神经网络 3. 损失函数和优化器示例:定义损失函数和优化器 4. 训练循环示例:训练循环 5. 评估和测试示例:评估模型 6. 保存和加载模…...

C++ | Leetcode C++题解之第338题比特位计数
题目: 题解: class Solution { public:vector<int> countBits(int n) {vector<int> bits(n 1);for (int i 1; i < n; i) {bits[i] bits[i & (i - 1)] 1;}return bits;} };...
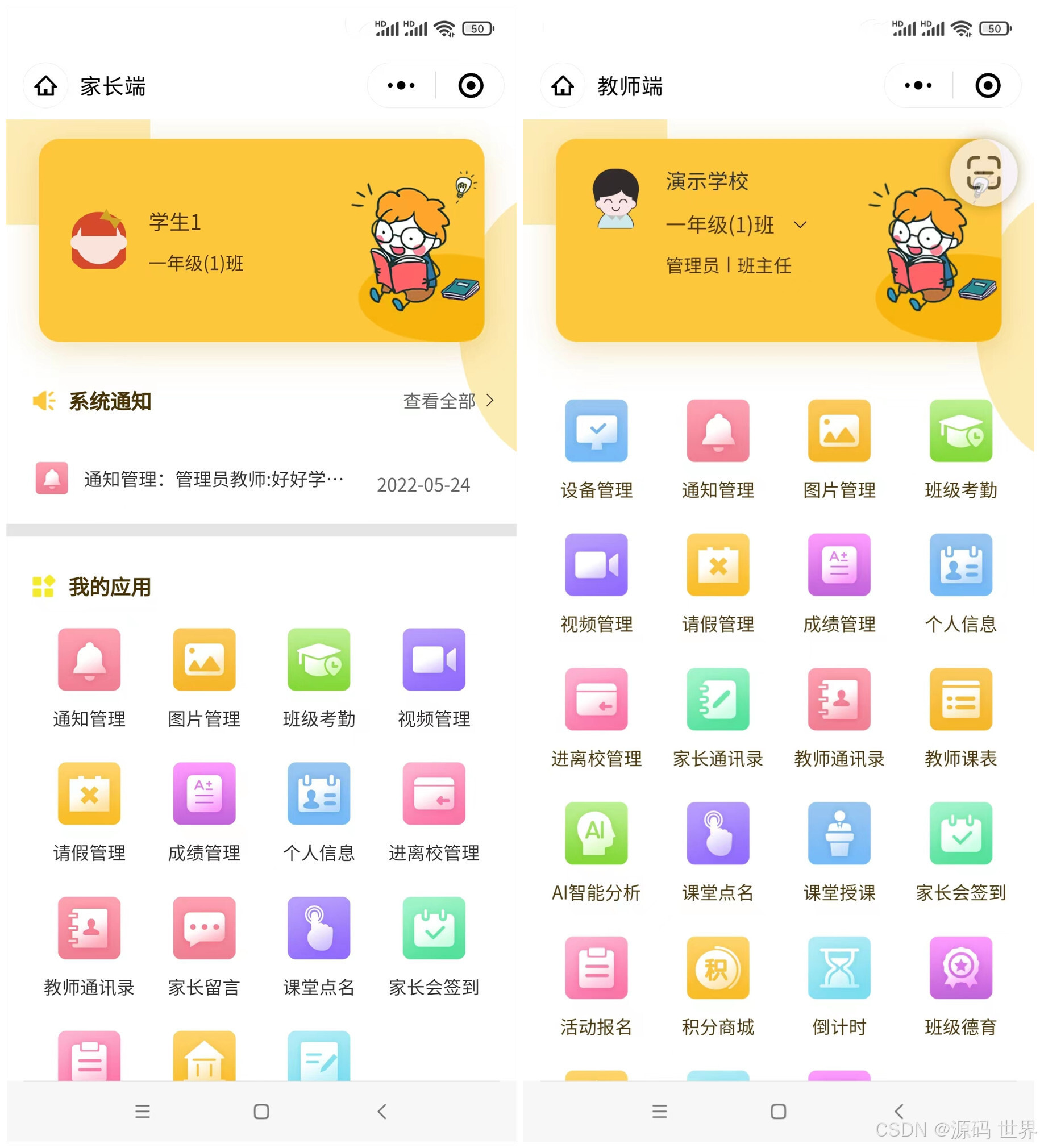
智慧校园云平台电子班牌系统源码,智慧教育一体化云解决方案
智慧校园云平台电子班牌系统,利用先进的云计算技术,将教育信息化资源和教学管理系统进行有效整合,实现生态基础数据共享、应用生态统一管理,为智慧教育建设的统一性,稳定性,可扩展性,互通性提供…...

数据库系统 第17节 数据仓库 案例赏析
下面我将通过几个具体的案例来说明数据仓库如何在不同的行业中发挥作用,并解决实际业务问题。 案例 1: 零售业 背景: 一家大型零售商希望改进其库存管理和市场营销策略,以提高销售额和顾客满意度。 解决方案: 数据仓库: 构建一个数据仓库࿰…...
硬件面试经典 100 题(71~90 题)
71、请问下图电路的作用是什么? 该电路实现 IIC 信号的电平转换(3.3V 和 5V 电平转换),并且是双向通信的。 上下两路是一样的,只分析 SDA 一路: 1) 从左到右通信(SDA2 为输入状态&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
