Educational Codeforces Round 169 (Rated for Div. 2)(ABCDE)
A. Closest Point
签到
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
int n,m;
int q[N];
void solve()
{cin>>n;_rep(i,1,n)cin>>q[i];if(n!=2)cout<<"NO\n";else if(abs(q[1]-q[2])!=1)cout<<"YES\n";else cout<<"NO\n";return ;
}B. Game with Doors
题意:已知房间和房间初始之间没有门,加门之后房间和房间之间就相互不连通,给定两个区间[l,r],[L,R],问至少加多少扇门可以使得区间各自选一个点,这两个点一定不连通
手玩几个例子就可以发现
给定的区间没有交集的时候用一个门隔断即可
有交集的话交集(假设大小为x)内部的门一定要选上也就是x-1
然后就是边界,假设左端点不同那么左端点靠右的左边还要额外加一扇门,右端点同理
void solve()
{int a,b,c,d;cin>>a>>b>>c>>d;int x=max(a,c),y=min(b,d);if(a==c&&b==d)cout<<b-a<<'\n';else if(x>y)cout<<"1\n";else {int res=0;if(a!=c)res++;if(b!=d)res++;cout<<y-x+res<<'\n';}return ;
}C. Splitting Items
A,B玩家玩游戏,n个物品都有成本,从A开始轮流拿,假设A一共拿的成本为a,B一共拿的成本为b,那么A要使a-b最大化,B要使a-b最小化,现在B可以加k个成本(k可以分配给任意物品),问最终a-b最小值
思路:假设B不能加成本,A,B显然每次都拿最大值,那么从大到小排序,(编号从1开始比)A拿奇数位,B拿偶数位即可,现在B可以偷偷加成本,那么显然肯定是贪心的拿每个偶数位加成本,但是不能超过前一个奇数位,因为超过的话这一位排序之后就比前一个大了所以排在前一个前面,所以这一位反而变成了奇数位,所以最终偶数位加成本不超过前一个奇数位即可
代码实现:
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
int n,m,k;
int q[N];
void solve()
{cin>>n>>k;_rep(i,1,n)cin>>q[i];sort(q+1,q+1+n,greater<>());int a=0,b=0;for(int i=1;i<=n;i+=2){a+=q[i];if(i+1<=n){b+=q[i+1]+min(q[i]-q[i+1],k);k-=min(q[i]-q[i+1],k);}}cout<<a-b<<"\n";return ;
}D. Colored Portals
题意:每一个点对应两个字母,然后点与点之间如果有一个字母相同则可以连一条无向边,权重为两个点下标之差,给定n个点,m次询问,每次询问两个点的下标,要求找到两个点之间的最短路,如果没有则输出-1
思路:一共只有四个字母,可以发现询问的时候只要两个点有一个相同字母,则最短路肯定是两个点直接连边,否则要找一个中转站,两点通过中转站连接,这个中转站显然只要满同不等于a点的两个字母和b点对应的两个字母,其实也相当于这个中转站的字母组成就是a点两个字母取一个,b点两个字母取一个,那就一定能满足题目连边的条件起到中转的目的,为了实现路径最短,显然要在a点左边和右边分别找到第一个中转站或者在b点左边和b点右边找一个中转站,假设坐标为x,那么最短路长度就是abs(b-x)+abs(a-x),实际上最麻烦的点在于:假设要找"BG" 如何找到当前坐标前面第一个"BG”和后面第一个"BG",那么把所有6种字母组合从1~6编号,然后求pre数组和next数组的时候遍历6个编号即可,具体实现在下面代码里体现
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <cmath>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define pp pop_back()
#define int long long
#define laile cout<<"laile"<<endl
#define lowbit(x) ((x)&(-x))
#define double long double
#define sf(x) scanf("%lld",&x)
#define sff(x,y) scanf("%lld %lld",&x,&y)
#define sd(x) scanf("%Lf",&x)
#define sdd(x,y) scanf("%Lf %Lf",&x,&y)
#define _for(i,n) for(int i=0;i<(n);++i)
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
#define _pre(i,a,b) for(int i=(a);i>=(b);--i)
#define all(x) (x).begin(), (x).end()
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
typedef unsigned long long ULL;
typedef pair<int,int>PII;
const int N=1e6+10,INF=4e18;
int n,m;
int qian[7][N];
string s[N];
int id[255];
int get(char a,char b)//编号
{if(id[a]>id[b])swap(a,b);if(id[a]==1)return id[b]-1;else if(id[a]==2)return id[b]+1;else return 6ll;
}
void init()
{id['B']=1;id['G']=2;id['R']=3;id['Y']=4;
}
int pre[N][10],ne[N][10];//pre[i][j]表示i位置第j个字符串的编号(假设为"BG")的前面第一个"BG"的位置
void solve()
{cin>>n>>m;_rep(i,1,n)cin>>s[i];int now[10];_rep(i,1,6)now[i]=0;_rep(i,1,n){ _rep(k,1,6)pre[i][k]=now[k];now[get(s[i][0],s[i][1])]=i;}_rep(i,1,6)now[i]=n+1;_pre(i,n,1){_rep(k,1,6)ne[i][k]=now[k];now[get(s[i][0],s[i][1])]=i;}while(m--){int a,b;cin>>a>>b;if(a>b)swap(a,b);int res=INF;for(auto i:s[a])for(auto j:s[b]){if(i==j)res=b-a;else{int now=get(i,j);if(pre[a][now])res=min(res,abs(a-pre[a][now])+abs(b-pre[a][now]));if(pre[b][now])res=min(res,abs(a-pre[b][now])+abs(b-pre[b][now]));if(ne[b][now]!=n+1)res=min(res,abs(a-ne[b][now])+abs(b-ne[b][now]));
// if(ne[a][now]!=n+1)//这里没必要了因为如果中转点在中间的话那么答案就是b-a,那么前面的pre[b][now]显然可以遍历到
// res=min(res,abs(a-ne[a][now])+abs(b-ne[a][now]));}}if(res==INF)cout<<"-1\n";else cout<<res<<'\n';}return ;
}
signed main()
{IOS;init();int T=1;cin>>T;while(T--)solve();return 0;
}E. Not a Nim Problem
题意,Alice和Bob做游戏,一共给定n堆石子,A先开始,每次可以从一堆石子(假设为y)中拿掉一部分(假设为x),那么一定要保证gcd(x,y)=1,最后轮到谁没有石子了谁就输了,对方就赢了
显然要用到NIM游戏的结论,所以现在要求的就是输入规模1~1e7的每一个数字的sg值
首先看一下一堆石子假设为x,那么x能走到哪些点?
首先x在满足gcd(x,y)==1的时候拿掉y个石子的所有情况构成了一个集合,可以发现和拿掉之后剩余石子x-y构成的集合一定是一样的,因为剩余的石子x-y一定也满足gcd(x,x-y)==1,为什么?假设gcd(x,x-y)=z那么x和y一定都是z的倍数(假设x=a*z,y=b*z,a>b并且gcd(a,b)=1),那么x-y=(a-b)*z,显然可以发现gcd(x,x-y)=z(因为a,b是互质所以a,a-b也互质,PS:假设a,a-b不互质那么a,a-(a-b);也就是a.b不互质与a,b互质矛盾,所以a,a-b必定互质))
现在就可以画图找规律了

手玩以下可以发现(黑色点为石子数量,红色为sg值)
1.sg[1]=0
2.石子数量为偶数时候走不到任何sg值为0的点,所以sg[偶数]=0
举个例子,现在当前只知道sg[0~5],发现sg[2]=sg[4]=0,sg[0]就不管了因为只有1能走到0,那么我现在要求sg[6],要使得6走到sg值为0的点那就只能走到2,4但是两个偶数的gcd肯定不会为1
3.sg[质数]=质数在质数序列中的编号,比如sg[3]=2,sg[5]=3,可以发现sg[x]能走到的最大sg值是sg[x‘
],x'为这个质数的上一个质数,所以sg[x]=sg[x']+1
4.对于其他的x,sg[x]=sg[x''],其中x''为x的最小质因数
看上面的图中的9,他的最小质因数是3,首先这个9至少能达到sg[3]-1(也就是sg[9]=sg[3]),因为3是它的质因数,所以它同样可以走到相对于3的所有能走到的点。
然后看一下9能否走到sg[3]?(为什么突然要看这个点呢,因为图中的9走不到sg[3]所以看一下这种情况是不是必然的)看一下sg[3]为什么为sg[3],是因为3这个数可以走到0,1这两个状态(注意是状态(sg值)而不是石子数量)而走不到2这个状态,还有哪些数能满足这个性质?很显然可以发现只要以3为质因数的数字都满足这个性质,回到这一段开始的问题,可以发现要走到sg[3]一定要走到以3为质因数的数字,但是9不可能走到3为质因数的数字因为9和这个数字都是3的倍数,不满足题目要求,所以说9可以走到的状态一定断在了sg[3],那么就可以得到sg[9]=sg[3]
代码实现
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <cmath>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define pp pop_back()
#define int long long
#define laile cout<<"laile"<<endl
#define lowbit(x) ((x)&(-x))
#define double long double
#define sf(x) scanf("%lld",&x)
#define sff(x,y) scanf("%lld %lld",&x,&y)
#define sd(x) scanf("%Lf",&x)
#define sdd(x,y) scanf("%Lf %Lf",&x,&y)
#define _for(i,n) for(int i=0;i<(n);++i)
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
#define _pre(i,a,b) for(int i=(a);i>=(b);--i)
#define all(x) (x).begin(), (x).end()
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
typedef unsigned long long ULL;
typedef pair<int,int>PII;
const int N=1e7+10,INF=4e18;
int n,m;
int prime[N],cnt,sg[N],minprime[N];
bool st[N];
void init()
{for(int i=2;i<N;i++){if(!st[i])prime[cnt++]=i;for(int j=0;prime[j]*i<N;j++){st[prime[j]*i]=true;minprime[prime[j]*i]=prime[j];if(i%prime[j]==0)break;}}for(int i=0;i<cnt;i++)sg[prime[i]]=i+1;return;
}
void solve()
{cin>>n;int res=0;while(n--){cin>>m;if(m%2==0)m=2;else if(st[m])m=minprime[m];res^=sg[m];}if(res)cout<<"Alice\n";else cout<<"Bob\n";return ;
}
signed main()
{IOS;int T=1;cin>>T;init();sg[1]=1;sg[2]=0;while(T--)solve();return 0;
}相关文章:

Educational Codeforces Round 169 (Rated for Div. 2)(ABCDE)
A. Closest Point 签到 #define _rep(i,a,b) for(int i(a);i<(b);i) int n,m; int q[N]; void solve() {cin>>n;_rep(i,1,n)cin>>q[i];if(n!2)cout<<"NO\n";else if(abs(q[1]-q[2])!1)cout<<"YES\n";else cout<<"…...

成为Python砖家(2): str 最常用的8大方法
str 类最常用的8个方法 str.lower()str.upper()str.split(sepNone, maxsplit-1)str.count(sub[, start[, end]])str.replace(old, new[, count])str.center(width[, fillchar])str.strip([chars])str.join(iterable) 查询方法的文档 根据 成为Python砖家(1): 在本地查询Pyth…...
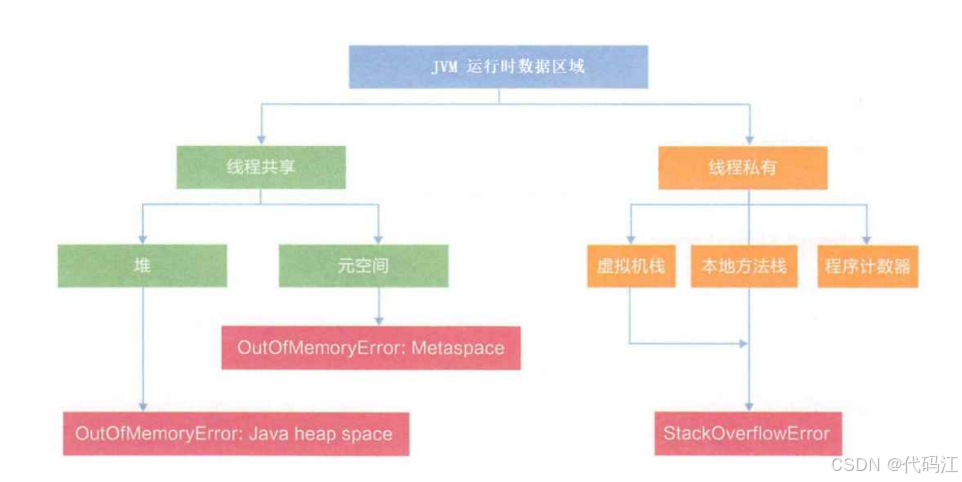
深入理解JVM运行时数据区(内存布局 )5大部分 | 异常讨论
前言: JVM运行时数据区(内存布局)是Java程序执行时用于存储各种数据的内存区域。这些区域在JVM启动时被创建,并在JVM关闭时销毁。它们的布局和管理方式对Java程序的性能和稳定性有着重要影响。 目录 一、由以下5大部分组成 1.…...

JAVA根据表名获取Oracle表结构信息
响应实体封装 import lombok.AllArgsConstructor; import lombok.Builder; import lombok.Data; import lombok.NoArgsConstructor;/*** author CQY* version 1.0* date 2024/8/15 16:33**/ Data NoArgsConstructor AllArgsConstructor Builder public class OracleTableInfo …...

网络性能优化
网络性能优化是确保网络稳定性、速度和可靠性的关键步骤。优化过程通常包括诊断问题、识别瓶颈以及实施具体的解决方案。以下是关于如何进行网络性能优化的详细指南: 一、问题诊断 网络性能监控 网络流量分析工具:使用Wireshark、NetFlow、Ntop等工具监…...

[C++String]接口解读,深拷贝和浅拷贝,string的模拟实现
💖💖💖欢迎来到我的博客,我是anmory💖💖💖 又和大家见面了 欢迎来到C探索系列 作为一个程序员你不能不掌握的知识 先来自我推荐一波 个人网站欢迎访问以及捐款 推荐阅读 如何低成本搭建个人网站…...
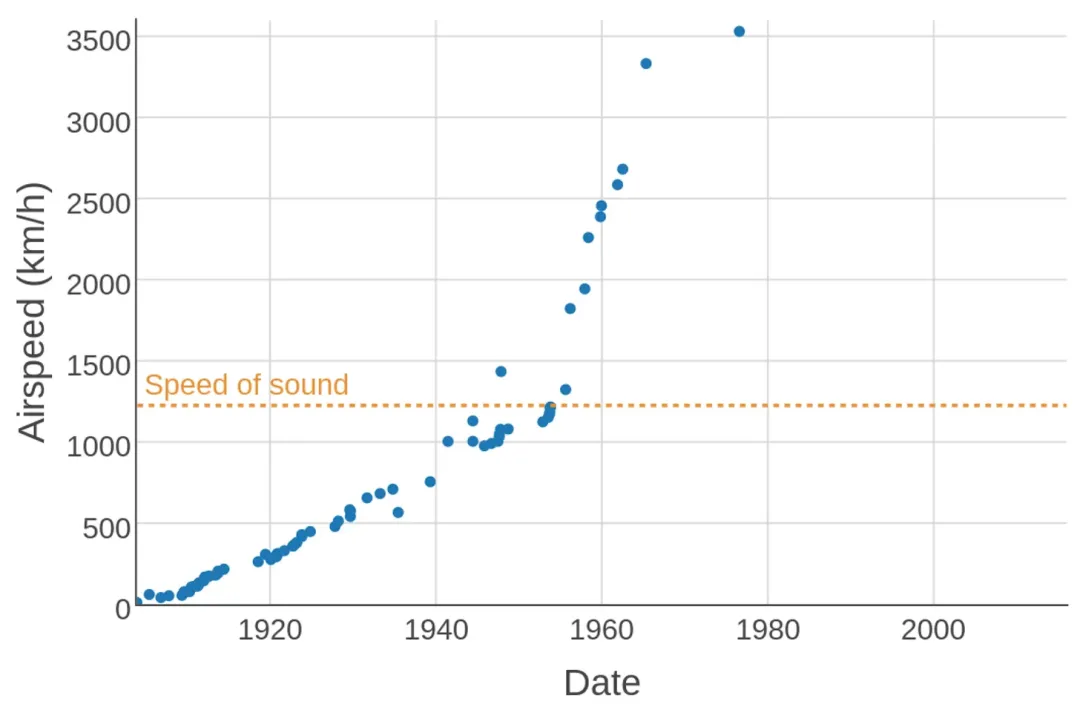
理性看待、正确理解 AI 中的 Scaling “laws”
编者按:LLMs 规模和性能的不断提升,让人们不禁产生疑问:这种趋势是否能一直持续下去?我们是否能通过不断扩大模型规模最终实现通用人工智能(AGI)?回答这些问题对于理解 AI 的未来发展轨迹至关重…...
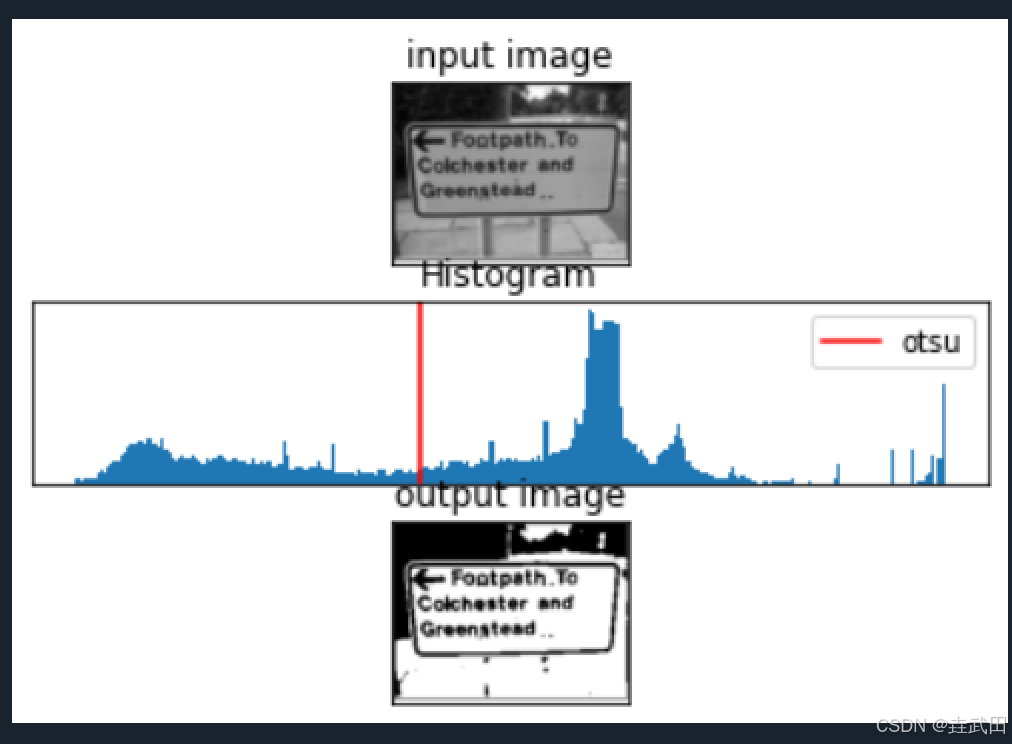
【OCR 学习笔记】二值化——全局阈值方法
二值化——全局阈值方法 固定阈值方法Otsu算法在OpenCV中的实现固定阈值Otsu算法 图像二值化(Image Binarization)是指将像素点的灰度值设为0或255,使图像呈现明显的黑白效果。二值化一方面减少了数据维度,另一方面通过排除原图中…...
Java - IDEA开发
使用IDEA开发Java程序步骤: 创建工程 Project;创建模块 Module;创建包 Package;创建类;编写代码; 如何查看JDK版本 Package介绍: package是将项目中的各种文件,比如源代码、编译生成的字节码、配置文件、…...
什么是内存优化表(In-Memory Table)?)
Oracle(62)什么是内存优化表(In-Memory Table)?
内存优化表(In-Memory Table)是指将表的数据存储在内存中,以提高数据访问和查询性能的一种技术。内存优化表通过利用内存的高速访问特性,显著减少I/O操作的延迟,提升数据处理的速度。这种技术在需要高性能数据处理的应…...
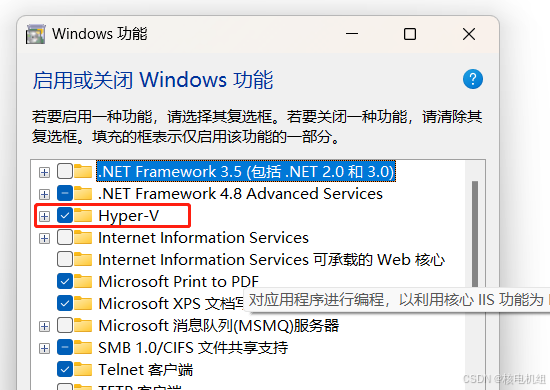
#window家庭版安装hyper-v#
由于window 11 家庭版没有hyper-v虚拟机服务,则需要安装一下,使用如下操作 1:新建一个txt文件,拷贝如下脚本到里面 pushd "%\~dp0" dir /b %SystemRoot%\servicing\Packages\*Hyper-V*.mum >hyper-v.txt for /f %%i in (findst…...

【云原生】Pass容器研发基础——汇总篇
云原生基础汇总 系列综述: 💞目的:本系列是个人整理为了云计算学习的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:每个知识点的修正和深入主要参考各平台大佬的文章,…...
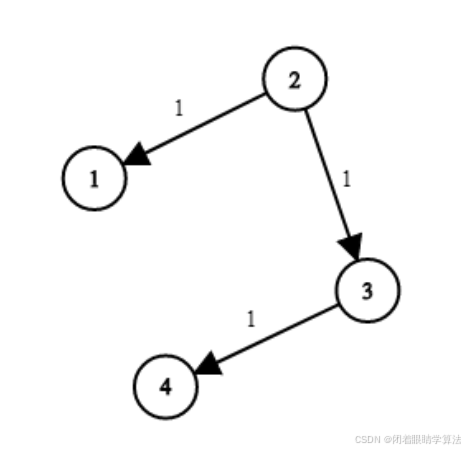
【Py/Java/C++三种语言详解】LeetCode743、网络延迟时间【单源最短路问题Djikstra算法】
可上 欧弟OJ系统 练习华子OD、大厂真题 绿色聊天软件戳 od1441了解算法冲刺训练(备注【CSDN】否则不通过) 文章目录 相关推荐阅读一、题目描述二、题目解析三、参考代码PythonJavaC 时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 相关推荐阅读 …...

交替输出
交替输出 题目:线程 1 输出 a 5 次,线程 2 输出 b 5 次,线程 3 输出 c 5 次。现在要求输出 abcabcabcabcabc wait notify 版 public class SyncWaitNotify {private volatile int flag;private volatile int loopNumber;public SyncWaitNo…...
——更改html内数据)
JS(三)——更改html内数据
获取 DOM 元素,然后修改其属性或内容。使用 getElementById 方法获取特定 ID 的元素: <p id"myParagraph">这是初始的文本</p> const paragraph document.getElementById(myParagraph); paragraph.innerHTML 这是修改后的文本…...

CSS小玩意儿:文字适配背景
一,效果 二,代码 1,搭个框架 添加一张背景图片,在图片中显示一行文字。 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" conte…...
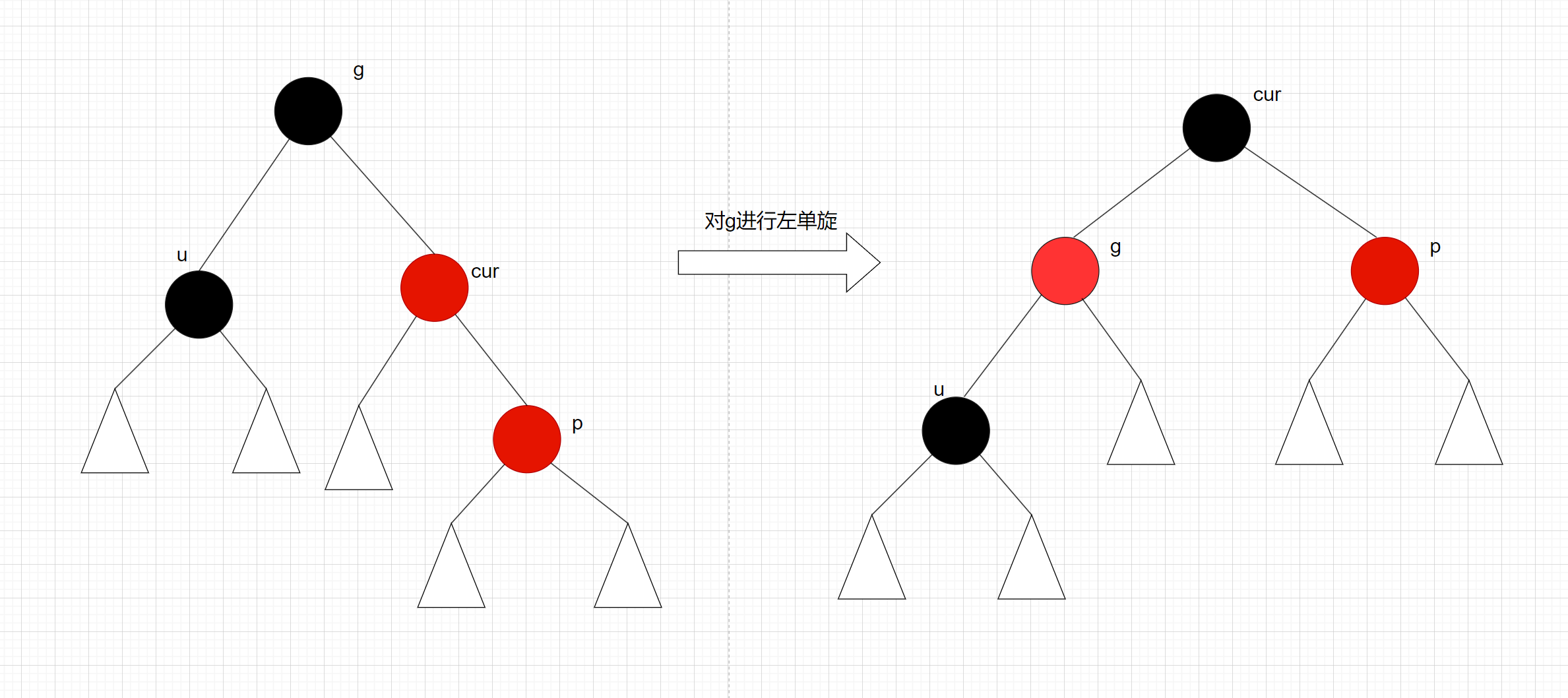
C++:平衡二叉搜索树之红黑树
一、红黑树的概念 红黑树, 和AVL都是二叉搜索树, 红黑树通过在每个节点上增加一个储存位表示节点的颜色, 可以是RED或者BLACK, 通过任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树能够确保没有一条路径会比…...

CentOS 7 系统优化
CentOS 7 系统优化 1、配置YUM源 阿里云的YUM源配置: CentOS 7使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repoCentOS 8使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS…...

扫雷游戏——附源代码
扫雷游戏的源代码比较简单,不设计比较复杂的代码,主要是多个函数的组合,每个函数执行自己的功能,最终支持游戏的完成。 1.菜单 我们需要一个提醒信息来让用户进行选择。 void menu() {printf("***********************\n&…...
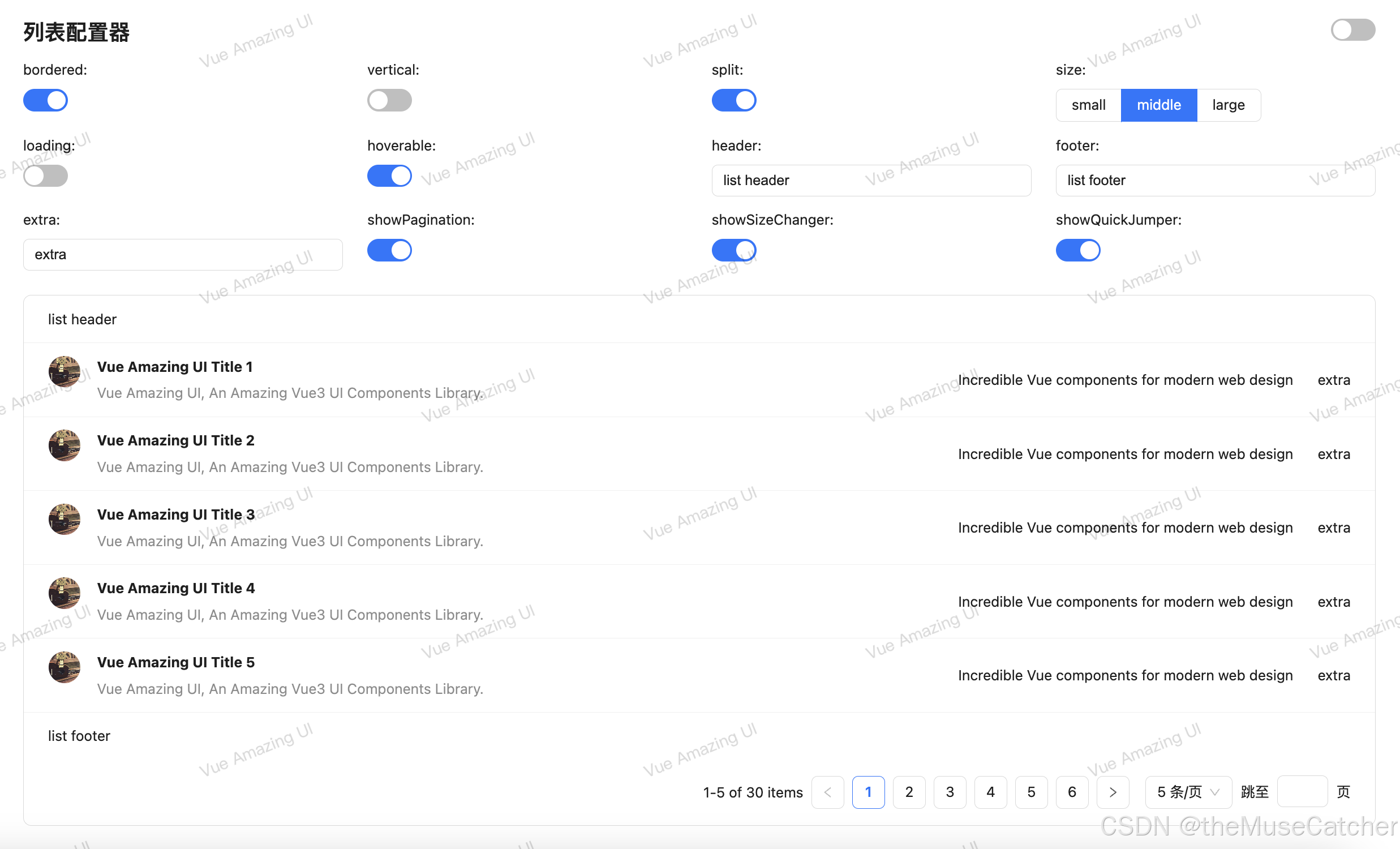
Vue3列表(List)
效果如下图:在线预览 APIs List 参数说明类型默认值bordered是否展示边框booleanfalsevertical是否使用竖直样式booleanfalsesplit是否展示分割线booleantruesize列表尺寸‘small’ | ‘middle’ | ‘large’‘middle’loading是否加载中booleanfalsehoverable是否…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
