spfa()算法(求最短路)
spfa算法是对bellman_ford算法的优化,大部分求最短路问题都可以用spaf算法来求。
注意:
(1)如若图中有负权回路,不能用spfa算法,要用bellman_ford算法;若只有负权边,则可以用
spfa算法
(2)Dijikstra算法适用于图中全都是正权边
spfa算法
step1:
初始化
step2:
取出队头结点,弹出队头,遍历队头结点的子结点,更新距离
step3:
如若第一次更新距离(st[j] == false),将结点编号加入队列。
step4:
重复循环,直至队列没有结点编号,说明到头了。
题目如下:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 impossible。
数据保证不存在负权回路。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 impossible。
数据范围
1≤n,m≤105,
图中涉及边长绝对值均不超过 10000。
解答代码如下:
//主要解决三个问题:
//(1)st数组有啥用:if(st[j] == true)//提高速度//处理重边
//(2)用spfa时,为啥图中不能有负权回路:模拟一遍就会了,因为while(q.size())
//(3)为什么要用队列?
#include<iostream>
#include<cstring>
#include<queue>using namespace std;const int N = 100010;int n,m;
int e[N],ne[N],h[N],idx,w[N];
int dist[N];
bool st[N];//如st[i],记录的是编号i结点是否是在队列中void add(int a,int b,int c)
{e[idx] =b;w[idx] = c;ne[idx] = h[a];h[a] = idx;idx++;
}int spfa()
{memset(dist,0x3f,sizeof(dist));dist[1] = 0;queue<int > q;q.push(1);//队列q中存储的是上一次循环中被更新最短路径的结点编号st[1] = true;//st数组中存储的是此时编号 i 结点是否在队列中while(q.size()){int t = q.front();q.pop();//q中只存储上一次循环中被确定最短路径长的结点的编号,再上一次的会被弹出st[t] = false;for (int i = h[t];i != -1;i = ne[i]){int j =e[i];if (dist[j] > dist[t] + w[i])//通过if语句判定,说明编号 j 结点需要更新{dist[j] = dist[t] + w[i];if (!st[j])//判断q会不会出现重复的结点{q.push(j);//如果这个结点的距离是第一次被更新(初始值都是0x3f3f3f3f)//那么就进入队列,在下一次循环中,q队列中存储的就是上一次循环//更新路径长度的结点编号了st[j] = true;//标记编号 j 结点}}}}return dist[n];}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n >> m;memset(h,-1,sizeof(h));while(m--){int a,b,c;cin >> a >> b >> c;add(a,b,c);}int t = spfa();if (t == 0x3f3f3f3f)cout << "impossible";elsecout << t;return 0;
}模拟过程:




(1) 为什么用队列?
spfa算法中使用队列是为了优化bellman_ford算法中的遍历每一条边来找到编号 t 结点的子结点
使用队列后,如此时t = 1,那么这一次循环中更新了 dist (第一次走到某结点时,都会更新,因为第一次走到某结点时的 dist 都是 0x3f3f3f3f )的结点就是编号 1 结点的子结点,加更新了 dist加入到队列,下次循环时,直接取出,就可以省略遍历所有边
(2)为什么不能有负权回路

(3)st数组有什么用
我认为的作用之一就是处理重边

相关文章:

spfa()算法(求最短路)
spfa算法是对bellman_ford算法的优化,大部分求最短路问题都可以用spaf算法来求。 注意: (1)如若图中有负权回路,不能用spfa算法,要用bellman_ford算法;若只有负权边,则可以用 spf…...

聊聊国产数据库的生态系统建设
生态系统是指在自然界中,生物与环境构成统一的整体,之间相互影响相互制约,并在一定时期内处于相对稳定的动态平衡状态。所谓数据库的生态系统,从用户的角度看,就是充分打通产品使用过程中上下游的关联,使其…...
JDK源码解析:LinkedList
1、背景 我们咨询一下腾讯混元大模型,什么是“LinkedList”。 以下是混元大模型的回答: LinkedList 是 Java 集合框架中的一种数据结构,它实现了 List 和 Deque 接口。LinkedList 是一个双向链表,这意味着每个元素都包含对前一个和…...

drawio的问题
drawio的问题 先给出drawio的链接https://app.diagrams.net/ 我在用overleaf写论文的过程中,发现了一个问题,就是使用drawio画好图之后,只能保存以下几个选项: 但是不管是什么类型,在overleaf上面图片都不显示。如果…...

零基础学习Redis(3) -- Redis常用命令
Redis是一个 客户端-服务器 结构的程序,Redis客户端和服务器可以在同一台主机上,也可以在不同主机上,客户端和服务器之间通过网络进行通信。服务器端负责存储和管理数据。客户端则可以通过命名对服务端的数据进行操作。 Redis客户端有多种&a…...

响应式Web设计:纯HTML和CSS的实现技巧-1
响应式Web设计(Responsive Web Design, RWD)是一种旨在确保网站在不同设备和屏幕尺寸下都能良好运行的网页设计策略。通过纯HTML和CSS实现响应式设计,主要依赖于媒体查询(Media Queries)、灵活的布局、可伸缩的图片和字…...
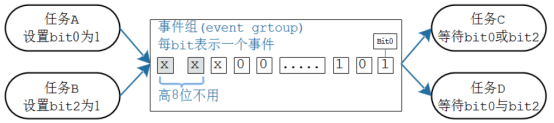
FrereRTOS事件组
文章目录 一、事件组概念与操作1、事件组的概念2、事件组的操作 二、事件组函数1、创建2、删除3、设置事件4、等待事件5、同步点 三、示例:广播四、示例:等待一个任意事件五、示例: 等待多个事件都发生 学校组织秋游,组长在等待: …...

【经典算法】BFS_最短路问题
目录 1. 最短路问题介绍2. 算法原理和代码实现(含题目链接)1926.迷宫中离入口最近的出口433.最小基因变化127.单词接龙675.为高尔夫比赛砍树 3. 算法总结 1. 最短路问题介绍 最短路径问题是图论中的一类十分重要的问题。本篇文章只介绍边权为1(或边权相同)的最简单的最短路径问…...

【题目/训练】:双指针
引言 我们已经在这篇博客【算法/学习】双指针-CSDN博客里面讲了双指针、二分等的相关知识。 现在我们来做一些训练吧 经典例题 1. 移动零 思路: 使用 0 当做这个中间点,把不等于 0(注意题目没说不能有负数)的放到中间点的左边,等于 0 的…...

LLVM - 编译器后端-指令选择
一:概述 任何后端的核心都是指令选择。LLVM 实现了几种方法;在本篇文章中,我们将通过选择有向无环图(DAG)和全局指令选择来实现指令选择。 在本篇文章中,我们将学习以下主题: • 定义调…...
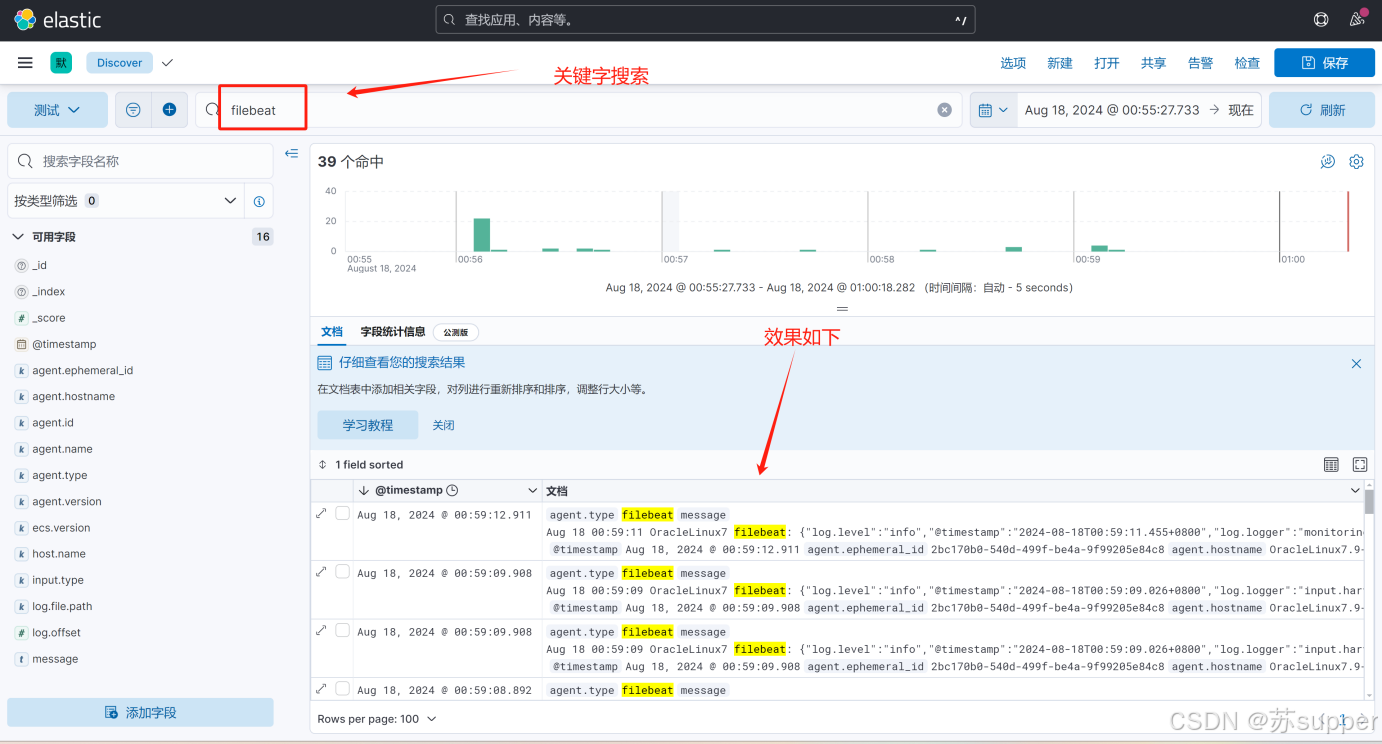
ES+FileBeat+Kibana日志采集搭建体验
1.环境准备 需要linux操作系统,并安装了docker环境 此处使用虚拟机演示。(虚拟机和docker看参考我之前写的文章) VirtualBox安装Oracle Linux 7.9全流程-CSDN博客 VirtualBox上的Oracle Linux虚拟机安装Docker全流程-CSDN博客 简单演示搭建ES…...

Dockerfile常用指令详解
Dockerfile 是一个用于定义 Docker 镜像构建过程的脚本文件,其中包含了一系列指令,用于指定如何构建和配置镜像。以下是一些常用的 Dockerfile 指令及其示例用法: 1. FROM 指定基础镜像,Dockerfile 必须以该指令开始。 示例&am…...

【vue】浏览器兼容相关
Vue.js 是一个流行的前端 JavaScript 框架,它支持构建单页应用和复杂的用户界面。Vue.js 的核心库本身对浏览器的支持情况如下: Vue.js 2.x 最低支持版本:IE9 及以上版本。特性支持:ES5。兼容性:Vue 2.x 在发布时就考…...

【区块链+金融服务】基于区块链的区域股权金融综合服务平台 | FISCO BCOS应用案例
区域性股权市场是我国资本市场的重要组成部分,是多层次资本市场体系的基石。区块链技术与区域性股权市场 分散特征天然匹配,从新型金融基础设施层面为场外参与各方提供公共的可信服务,以技术手段完善市场基础条 件,弥补区域性短板…...

string字符串和json对象相互转换问题
//响应体String responseStr EntityUtils.toString(response.getEntity());log.debug("下单响应码:{},响应体:{}",statusCode,responseStr);if(statusCode HttpStatus.OK.value()){JSONObject jsonObject JSONObject.parseObject(responseStr);if(jsonObject.cont…...

【生成式人工智能-十一一个不修改模型就能加速语言模型生成的方法】
一个加速语言模型生成的方法 现在语言模型的一个弊端speculative decoding预言家预测的问题 speculative decoding 模块的实现方法NAT Non-autoregressive模型压缩使用搜索引擎 一些更复杂些的speculative decoding 实现方式 speculative decoding 是一个适用于目前生成模型的加…...

Rust 错误处理
Rust 错误处理 Rust 是一种系统编程语言,以其内存安全、高并发和实用性而著称。在 Rust 中,错误处理是一个核心概念,它通过提供 Result 和 Option 类型来鼓励开发者显式地处理可能出现的错误,而不是依赖异常机制。本文将深入探讨 Rust 中的错误处理机制,包括 Result 和 O…...

程序与进程 linux系统
程序与进程 程序 ( program ): 通常为 binary program ,放置在储存媒体中(如硬盘、光盘、软盘、磁带等), 为实体文件的型态存在;二进制文件,比如静态 /bin/date…...

使用MongoDB构建AI:Story Tools Studio将生成式AI引入Myth Maker AI游戏
Story Tools Studio利用先进的生成式AI技术,打造沉浸式、个性化、无穷尽的情景体验。 Story Tools Studio创始人兼首席执行官Roy Altman表示:“我们的旗舰游戏Myth Maker AI采用的是我们自主研发的、以AI为驱动的专家指导型故事生成器MUSE,它…...
)
鸿蒙UIAbility组件概述(二)
鸿蒙UIAbility组件概述 UIAbility组件基本用法指定UIAbility的启动页面获取UIAbility的上下文信息 UIAbility组件与UI的数据同步使用EventHub进行数据通信使用AppStorage/LocalStorage进行数据同步 UIAbility组件间交互(设备内)启动应用内的UIAbility启动…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
