【杂乱算法】前缀和与差分
前缀和
文章目录
- 前缀和
- 一维
- 应用
- 二维
- 差分
- 一维
- 二维
- 扩展
- 1、前缀和与哈希表
一维
一个数组prefix中,第i个元素表示nums[0]至nums[i-1]的总和,那么我们就称这个prefix数组是nums数组的前缀和。
prefix [ i ] = ∑ j = 0 i nums [ j ] \text{prefix}[i] = \sum_{j=0}^{i} \text{nums}[j] prefix[i]=j=0∑inums[j]
应用
1、快速计算下标为[i , j]区间的和。
prefix[j+1]-prefix[i]即为下标[i , j]之间元素的总和。
二维
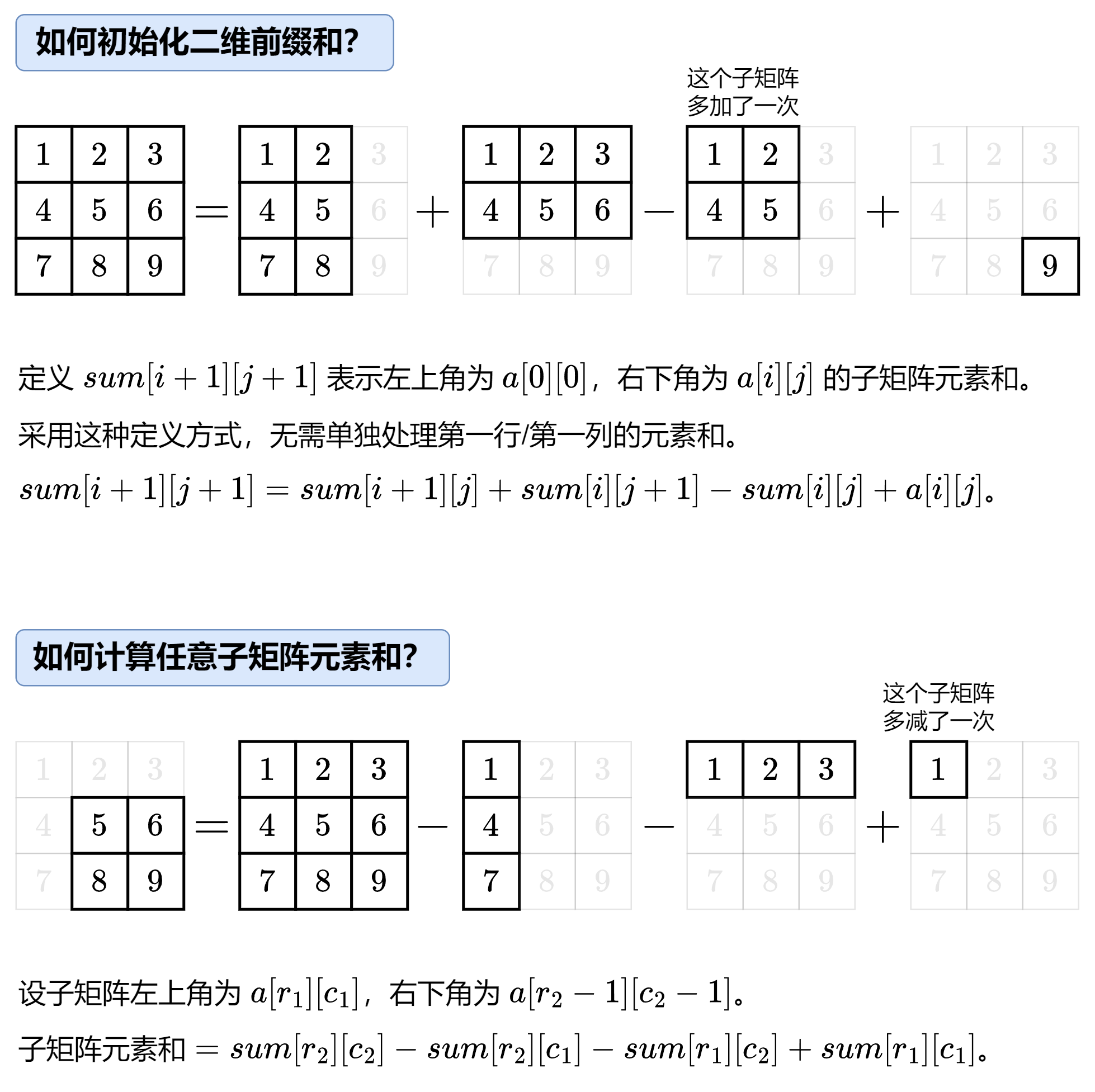
class NumMatrix {vector<vector<int>> sum;
public:NumMatrix(vector<vector<int>> &matrix) {int m = matrix.size(), n = matrix[0].size();sum.resize(m + 1, vector<int>(n + 1));for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + matrix[i][j];}}}// 返回左上角在 (r1,c1) 右下角在 (r2,c2) 的子矩阵元素和int sumRegion(int r1, int c1, int r2, int c2) {return sum[r2 + 1][c2 + 1] - sum[r2 + 1][c1] - sum[r1][c2 + 1] + sum[r1][c1];}
};作者:灵茶山艾府
链接:https://leetcode.cn/problems/range-sum-query-2d-immutable/solutions/2667331/tu-jie-yi-zhang-tu-miao-dong-er-wei-qian-84qp/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
差分
一维
所谓“差分”,是指原数组中每个元素与前一元素之差所形成的数组。
我们知道,对原数组进行诸位累加(前缀计算操作),所得到的数组为前缀和数组。差分数组,则是对其执行前缀计算后,能够得到原数组的那个数组 。
差分数组的主要作用,是帮助快速修改某段区间。
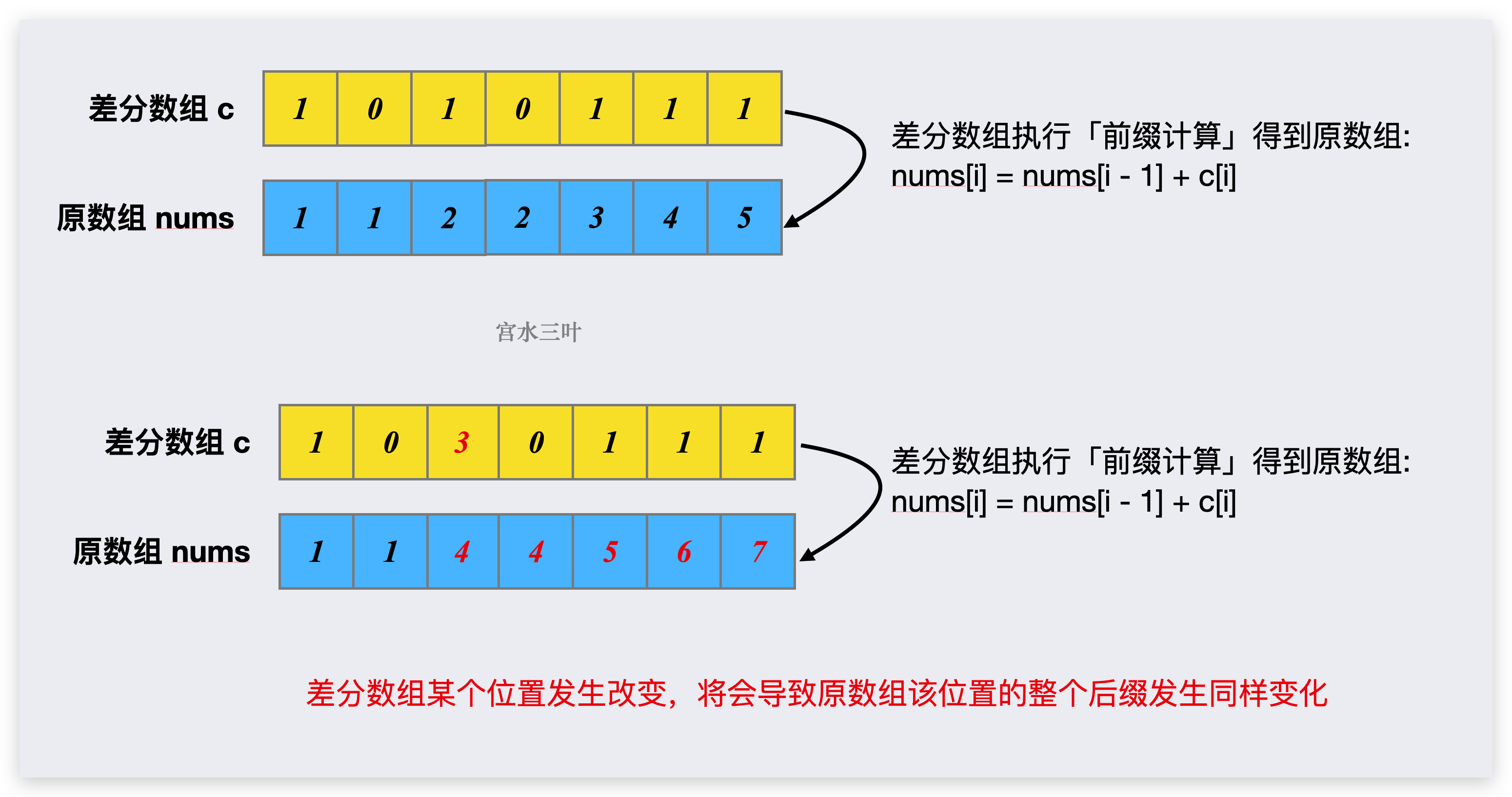
因此,当我们想要对原数组的 [l,r] 进行整体修改时,只需要对差分数组的l 和r+1 位置执行相应操作即可。
二维
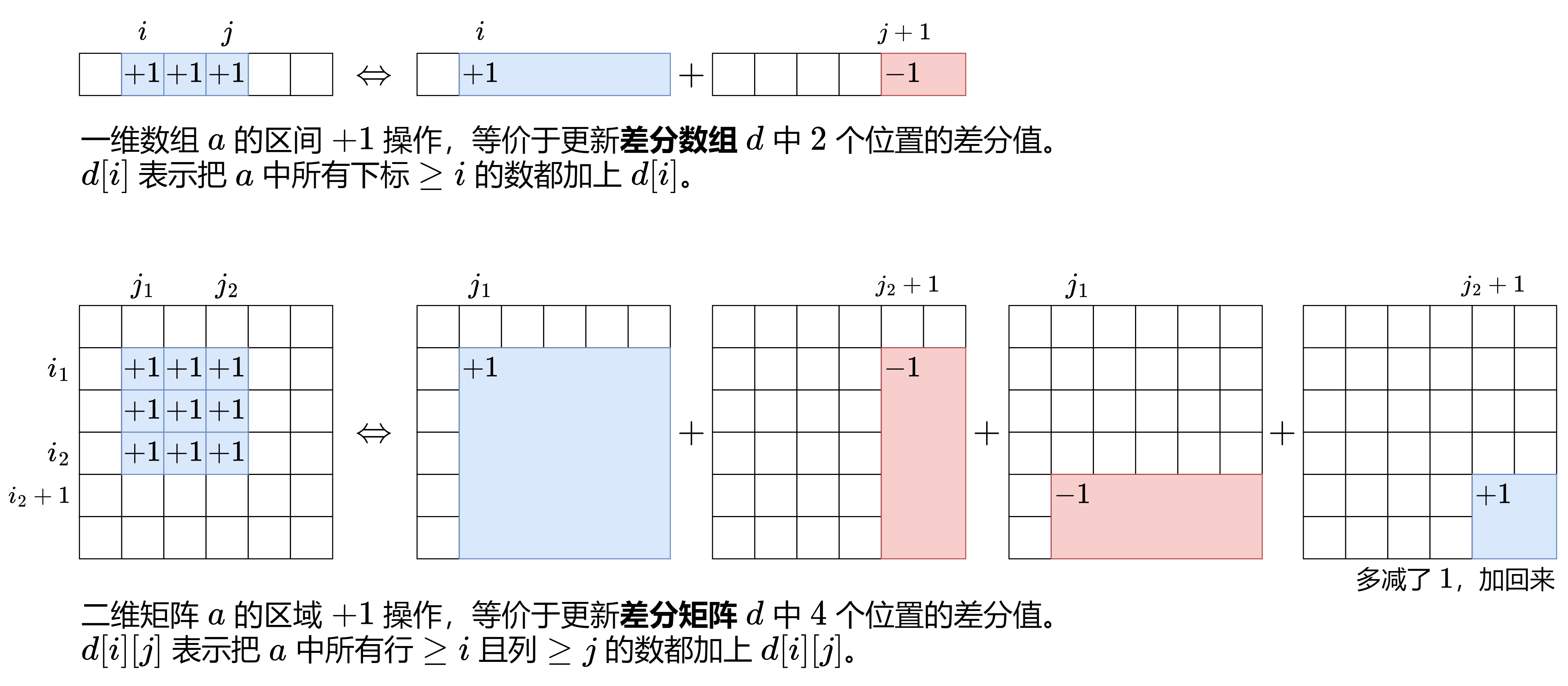
扩展
1、前缀和与哈希表
力扣560.和为k的子数组
借助哈希表中判定重复元素的功能,可以帮忙判断(当前的前缀和-K)是否出现在哈希表中,如果有那么久数量加一,如果没有就将当前前缀和压入哈希表。
class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> haxi; // 用于存储前缀和出现次数haxi[0] = 1; // 初始化,表示前缀和为0出现一次vector<int> qian(nums.size() + 1, 0); // 前缀和数组int ans = 0;// 计算前缀和for (int i = 1; i <= nums.size(); i++) {qian[i] = nums[i - 1] + qian[i - 1];}// 查找满足条件的子数组for (int i = 1; i <= nums.size(); i++) {int complement = qian[i] - k;if (haxi.find(complement) != haxi.end()) {ans += haxi[complement]; // 增加满足条件的子数组个数}haxi[qian[i]]++; // 更新当前前缀和的出现次数}return ans;}
};
或者也可以一次遍历即可。在遍历的同时判断(当前的前缀和-K)是否出现在哈希表中。
class Solution {
public:int subarraySum(vector<int>& nums, int k) {int ans = 0, s = 0;unordered_map<int, int> cnt{{0, 1}}; // s[0]=0 单独统计for (int x : nums) {s += x;// 注意不要直接 += cnt[s-k],如果 s-k 不存在,会插入 s-kans += cnt.contains(s - k) ? cnt[s - k] : 0;cnt[s]++;}return ans;}
};作者:灵茶山艾府
链接:https://leetcode.cn/problems/subarray-sum-equals-k/solutions/2781031/qian-zhui-he-ha-xi-biao-cong-liang-ci-bi-4mwr/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

【杂乱算法】前缀和与差分
前缀和 文章目录 前缀和一维应用 二维差分一维 二维扩展1、前缀和与哈希表 一维 一个数组prefix中,第i个元素表示nums[0]至nums[i-1]的总和,那么我们就称这个prefix数组是nums数组的前缀和。 prefix [ i ] ∑ j 0 i nums [ j ] \text{prefix}[i] \s…...
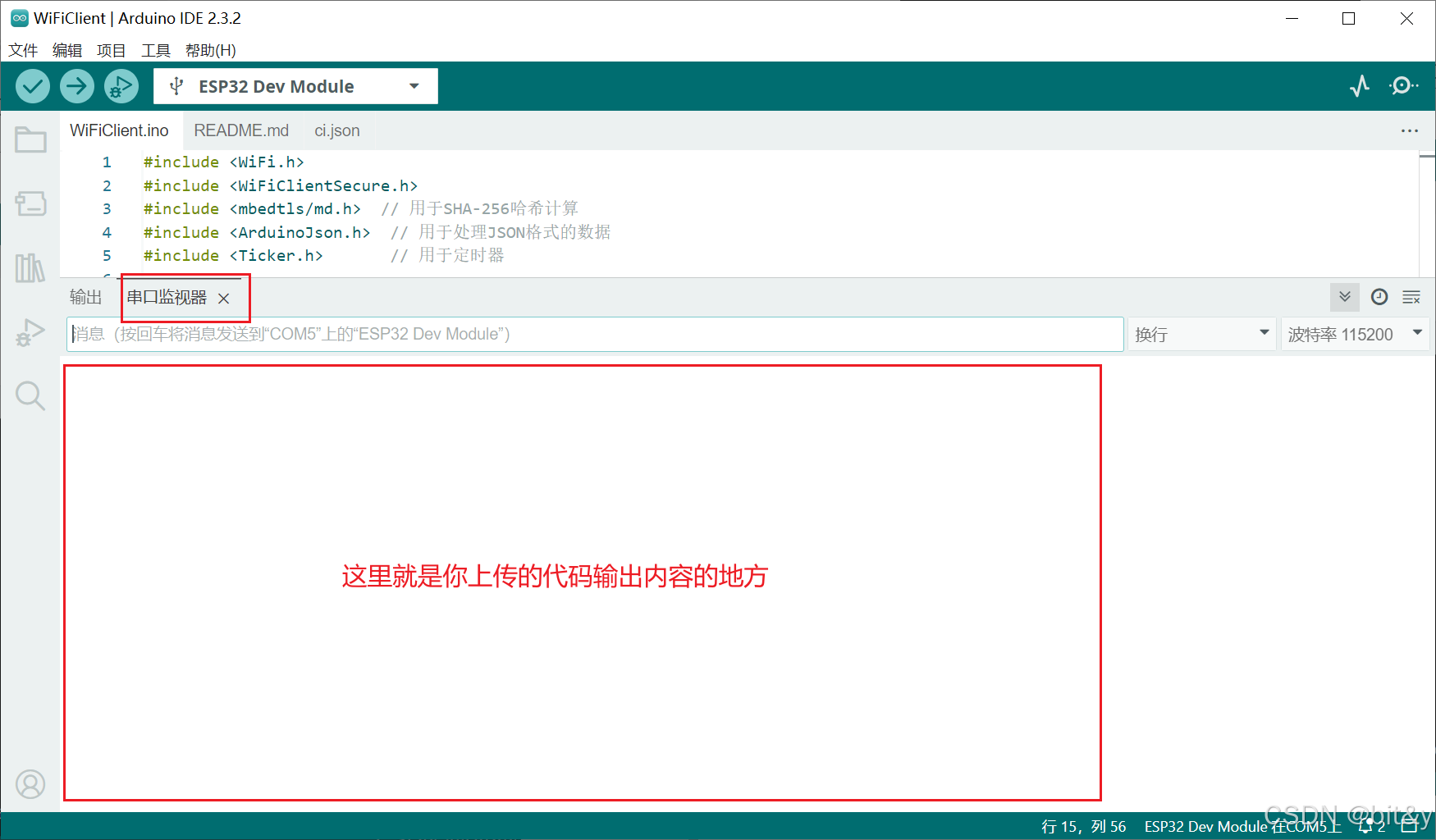
Arduino调试ESP32常见问题 exit status 1
问题1:代码上传(烧录)报Failed uploading: uploading error: exit status 1大概率原因:没有安装对应的驱动,我的ESP32驱动是CH340点击这里下载CH340 下载后打开,若出现乱码不用在意,点击第一个按…...

“决胜面试:高频题目与算法策略一览”
干货分享,感谢您的阅读! (暂存篇---后续会删除,完整版和持续更新见高频面试题基本总结回顾(含笔试高频算法整理)) 备注:引用请标注出处,同时存在的问题请在相关博客留言…...

Node-RED的安装
最近对Node-RED比较感兴趣,因为在上OpenHarmony课程的时候,一直想找一个可以通过MQTT控制设备的低代码客户端解决方案。第一次指导Node-RED是在试用聆思开发板的时候,它的云端就是使用的Node-RED。 在安装Node-RED之前,请确保您的…...

java中的Collections
Java 的集合框架(Collections Framework)提供了一组标准的数据结构接口和类,用于存储和操作数据。Java 集合类位于 java.util 包中,主要包括以下几个核心接口和实现类。 1. 核心接口 1.1. Collection 接口 Collection 是集合框架的根接口,但它本身并不提供任何直接实现…...
linux Qt QkeyEvent及驱动键盘按键捕获
基于正点原子 QT中有专门的类处理键盘事件的类QKeyEvent 1.include “QKeyEvent” 查看它的说明中的描述 也就是说接受按键事件在keyPressEvent和keyReleaseEvent这两个函数,继续查看 重构这个函数 查看输入的QKeyEvent类,发现有一个方法key返回哪一个按…...

【GH】【EXCEL】P6: Shapes
文章目录 componentslinepicture components line picture Picture A Picture object Input parameters: Worksheet (Generic Data) A Worksheet, Workbook, Range Object, Excel Application, or Text Worksheet NameName (Text) An optional object nameLocation (Point) A p…...
google浏览器chrome用户数据(拓展程序,书签等)丢失问题
一、问题背景 我出现这个情况的问题背景是:因为C盘块满了想清理一部分空间(具体看这:windows -- C盘清理_c盘softwaredistribution-CSDN博客),于是找到了更改AppDatta这个方法,但因为,当时做迁移…...
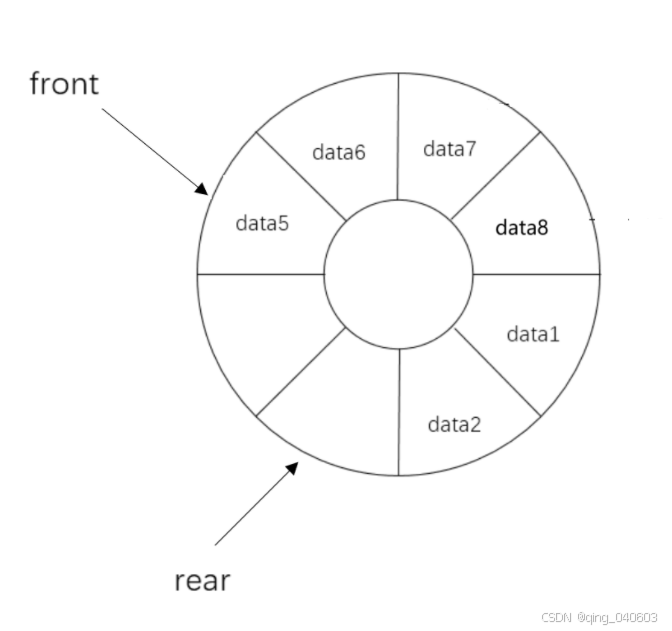
数据结构——链式队列和循环队列
目录 引言 队列的定义 队列的分类 1.单链表实现 2.数组实现 队列的功能 队列的声明 1.链式队列 2.循环队列 队列的功能实现 1.队列初始化 (1)链式队列 (2)循环队列 (3)复杂度分析 2.判断队列是否为空 (1)链式队列 (2)循环队列 (3)复杂度分析 3.判断队列是否…...

数据库死锁解决方法,学费了吗?
避免死锁:尽量设计良好的数据库结构,避免出现死锁的情况。可以使用合适的事务隔离级别,以及良好的并发控制策略。 死锁检测和回滚:当检测到死锁时,可以使用死锁检测算法来确定死锁的存在,并回滚其中一个或…...
API网关之Apache ShenYu
Apache ShenYu(原名Soul)是一个开源的API网关,旨在支持高性能、跨语言和云原生架构。它为管理和控制客户端与服务之间的数据流提供了一种高效且可扩展的解决方案。 文档见 Apache ShenYu 介绍 | Apache ShenYu 以下是Apache ShenYu的详细介…...

ECMA Script 6
文章目录 DOM (Document Object Model)BOM (Browser Object Model) let 和 const 命令constObject.freeze方法跨模块常量全局对象的属性 变量的结构赋值数组结构赋值对象解构赋值字符串解构赋值数值和布尔值的解构赋值函数参数解构赋值圆括号的问题 解构赋值的用途 字符串的扩展…...

如何在不破产的情况下训练AI模型
在当今的人工智能领域,训练复杂的AI模型——特别是大型语言模型(LLM)——需要巨大的算力支持。对于许多中小型企业来说,高昂的成本常常成为一个难以逾越的障碍。然而,通过采用一些策略和最佳实践,即使是在资源有限的情况下,也能有效地训练出高质量的AI模型。本文将介绍几…...

常用开发组件Docker部署保姆级教程
说明 本文总结了一些常用组件的Docker启动命令及过程,在开发过程中只需花费数分钟下载和配置即可完美使用这些服务。 Mysql MySQL 是一种开源关系数据库管理系统(RDBMS),目前由 Oracle 公司维护。MySQL 以其高性能、可靠性和易用…...
MySql高级视频笔记
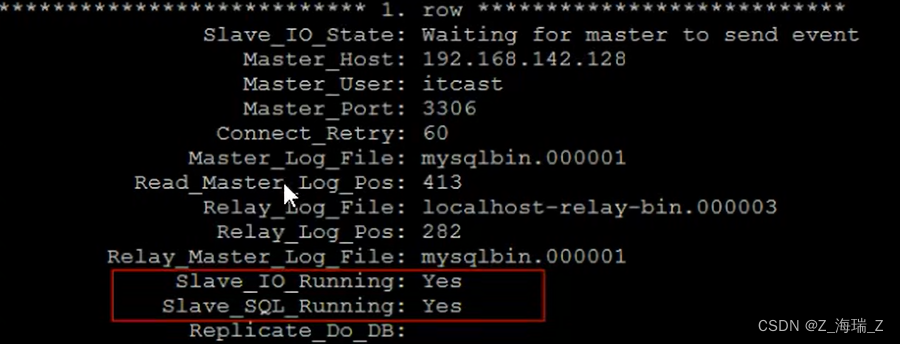
索引 索引 : 是帮助MySql高效查询数据的数据结构 优势&劣势 优势: 提高数据检索的效率, 降低数据库的IO成本通过索引列队数据进行排序, 降低数据的排序成本, 降低CPU的消耗 劣势: 索引维护了主键信息, 并指向表中数据记录, 也是占用磁盘空间的索引提高了查询效率, 但索引也…...

二十二、状态模式
文章目录 1 基本介绍2 案例2.1 Season 接口2.2 Spring 类2.3 Summer 类2.4 Autumn 类2.5 Winter 类2.6 Person 类2.7 Client 类2.8 Client 类的运行结果2.9 总结 3 各角色之间的关系3.1 角色3.1.1 State ( 状态 )3.1.2 ConcreteState ( 具体的状态 )3.1.3 Context ( 上下文 )3.…...
Spark环境搭建-Local
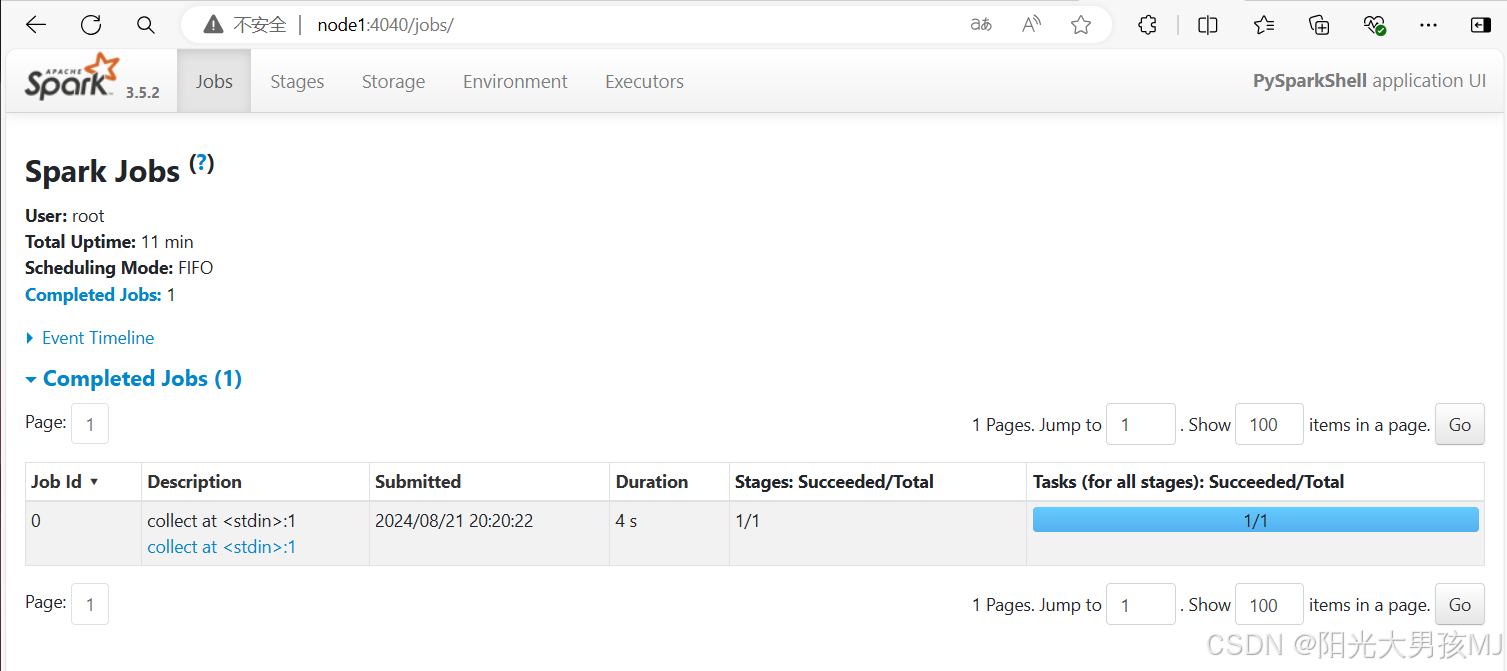
目录 Local下的角色分布: Anaconda On Linux 安装 (单台服务器) 1.下载安装 2.国内源 下载Spark安装包 1.下载 2.解压 3.环境变量 测试 监控 Local下的角色分布: 资源管理: Master:Local进程本身 Worker:L…...
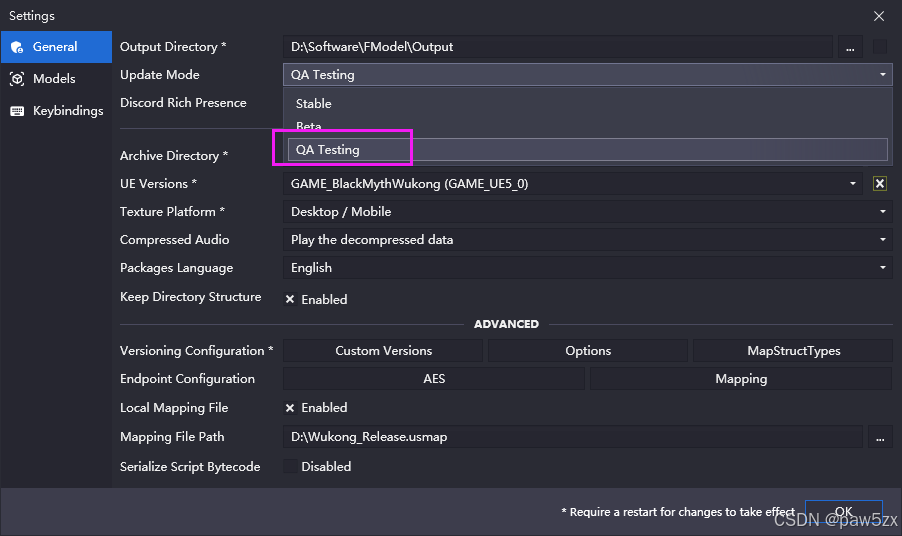
使用FModel提取黑神话悟空的资产
使用FModel提取黑神话悟空的资产 前言设置效果展示闲聊可能遇到的问题没有相应的UE引擎版本选项 前言 黑神话悟空昨天上线了,解个包looklook。 本文内容比较简洁,仅介绍解包黑神话所需的专项配置,关于FModel的基础使用流程,请见…...
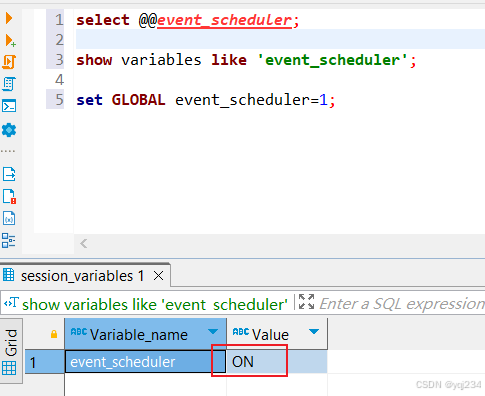
MYSQL定时任务使用手册
开发和管理数据库时,经常需要定时执行某些任务,比如每天备份数据库、每周统计报表等。MySQL提供了一个非常有用的工具,即事件调度器(Event Scheduler),可以帮助我们实现定时任务调度的功能。本文将介绍如何…...

SAP 预扣税配置步骤文档【Withholding Tax]
1. 配置预扣税的基本概念 预扣税是对某些支付进行扣除的税,可能适用于各种财务交易(例如,供应商支付、股息支付等)。预扣税通常包括几种类型,如个人所得税、企业所得税和其他税务种类。 2. 配置步骤 以下是一般的预…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
