力扣 | 递归 | 区间上的动态规划 | 486. 预测赢家
文章目录
- 一、递归
- 二、区间动态规划
LeetCode:486. 预测赢家

一、递归
注意到本题数据范围为 1 < = n < = 20 1<=n<=20 1<=n<=20,因此可以使用递归枚举选择方式,时间复杂度为 2 20 = 1024 ∗ 1024 = 1048576 = 1.05 × 1 0 6 2^{20} = 1024*1024=1048576=1.05 × 10^6 220=1024∗1024=1048576=1.05×106。
对于每一个先手都有两种选择方式,我们对该选择方式进行枚举。
我们定义递归函数 p r e d i c t predict predict表示玩家1在当前选择的情况下是否可以胜利,注意到每个玩家的玩法都会使他的分数最大化,因此对于玩家2的选择,如果存在一个选择使得玩家1输,那么该情况下玩家1都不能胜利(只要玩家2选择让自己赢的情况,那么玩家1就不能赢了)。但是对于玩家1的选择,存在一个选择能赢就算可以赢。

class Solution {
public:bool predictTheWinner(vector<int>& nums) {return predict(nums, 0, (int) nums.size() - 1, 0, 0, 0);}
private:bool predict(vector<int> & nums, int left, int right, int player, int score_1, int score_2){if(left > right){if(score_1 >= score_2) return true;else return false;}if(player == 0){//玩家一,存在一个赢就算赢了if(predict(nums, left + 1, right, player ^ 1, score_1 + nums[left], score_2)) return true;if(predict(nums, left, right - 1, player ^ 1, score_1 + nums[right], score_2)) return true;}else{//玩家二,存在一个玩家二赢,则玩家一必输。if(predict(nums, left + 1, right, player ^ 1, score_1, score_2 + nums[left]) &&predict(nums, left, right - 1, player ^ 1, score_1, score_2 + nums[right])) return true;}return false;}
};
二、区间动态规划
注意到这里是从大的数组中选择,让数组依次减小,我们也可以从数组小的开始转移到大数组,因为当小数组确定时,大数组也能确定。
我们可以定义 d p 1 [ i ] [ j ] [ p l a y e r ] dp1[i][j][player] dp1[i][j][player]表示在选择数组 [ i , j ] [i,j] [i,j]时, p l a y e r player player先手时,玩家1的分数;类似的有 d p 2 [ i ] [ j ] [ p l a y e r ] dp2[i][j][player] dp2[i][j][player]。
则有状态转移:
//玩家1先手dp1[i][j][0] = max(dp1[i + 1][j][1] + nums[i], dp1[i][j - 1][1] + nums[j]);if(dp1[i + 1][j][1] + nums[i] >= dp1[i][j - 1][1] + nums[j]){dp2[i][j][0] = dp2[i + 1][j][1];if(dp1[i + 1][j][1] + nums[i] == dp1[i][j - 1][1] + nums[j])dp2[i][j][0] = min(dp2[i + 1][j][1], dp2[i][j - 1][1]);}else{dp2[i][j][0] = dp2[i][j - 1][1];}
//玩家2先手dp2[i][j][1] = max(dp2[i + 1][j][0] + nums[i], dp2[i][j - 1][0] + nums[j]);if(dp2[i + 1][j][0] + nums[i] >= dp2[i][j - 1][0] + nums[j]){dp1[i][j][1] = dp1[i + 1][j][0];if(dp2[i + 1][j][0] + nums[i] == dp2[i][j - 1][0] + nums[j])dp1[i][j][1] = min(dp1[i + 1][j][0], dp1[i][j - 1][0]);}else{dp1[i][j][1] = dp1[i][j - 1][0];}
时间复杂度: O ( N 2 ) O(N^2) O(N2)

class Solution {
public:bool predictTheWinner(vector<int>& nums) {vector<vector<array<int, 2>>> dp1(nums.size(), vector<array<int, 2>>(nums.size(), array<int, 2>{}));vector<vector<array<int, 2>>> dp2(nums.size(), vector<array<int, 2>>(nums.size(), array<int, 2>{}));for(int i = 0; i < nums.size(); ++ i){dp1[i][i][0] = nums[i];dp2[i][i][1] = nums[i];}for(int k = 1; k < nums.size(); ++ k){for(int i = 0; k + i < nums.size(); ++ i){int j = i + k;//玩家1先手dp1[i][j][0] = max(dp1[i + 1][j][1] + nums[i], dp1[i][j - 1][1] + nums[j]);if(dp1[i + 1][j][1] + nums[i] >= dp1[i][j - 1][1] + nums[j]){dp2[i][j][0] = dp2[i + 1][j][1];if(dp1[i + 1][j][1] + nums[i] == dp1[i][j - 1][1] + nums[j])dp2[i][j][0] = min(dp2[i + 1][j][1], dp2[i][j - 1][1]);}else{dp2[i][j][0] = dp2[i][j - 1][1];}//玩家2先手dp2[i][j][1] = max(dp2[i + 1][j][0] + nums[i], dp2[i][j - 1][0] + nums[j]);if(dp2[i + 1][j][0] + nums[i] >= dp2[i][j - 1][0] + nums[j]){dp1[i][j][1] = dp1[i + 1][j][0];if(dp2[i + 1][j][0] + nums[i] == dp2[i][j - 1][0] + nums[j])dp1[i][j][1] = min(dp1[i + 1][j][0], dp1[i][j - 1][0]);}else{dp1[i][j][1] = dp1[i][j - 1][0];}}}return dp1[0][(int) nums.size() - 1][0] >= dp2[0][(int) nums.size() - 1][0];}
};
简化代码:(这个代码过了)
简化逻辑:玩家1先手,那么玩家1效益最大,玩家2应该效益要最低。
但这个逻辑感觉存在一定问题,因为玩家1先手,玩家1想要自己的效益最大,这个时候玩家2的效益是跟玩家1的选择有关的,因为棋局完全根据玩家1来决定。所以一开始我并没有直接使用min求解后手。
class Solution {
public:bool predictTheWinner(vector<int>& nums) {vector<vector<array<int, 2>>> dp1(nums.size(), vector<array<int, 2>>(nums.size(), array<int, 2>{}));vector<vector<array<int, 2>>> dp2(nums.size(), vector<array<int, 2>>(nums.size(), array<int, 2>{}));for(int i = 0; i < nums.size(); ++ i){dp1[i][i][0] = nums[i];dp2[i][i][1] = nums[i];}for(int k = 1; k < nums.size(); ++ k){for(int i = 0; k + i < nums.size(); ++ i){int j = i + k;//玩家1先手dp1[i][j][0] = max(dp1[i + 1][j][1] + nums[i], dp1[i][j - 1][1] + nums[j]);dp2[i][j][0] = min(dp2[i + 1][j][1], dp2[i][j - 1][1]);//玩家2先手dp2[i][j][1] = max(dp2[i + 1][j][0] + nums[i], dp2[i][j - 1][0] + nums[j]);dp1[i][j][1] = min(dp1[i + 1][j][0], dp1[i][j - 1][0]);}}return dp1[0][(int) nums.size() - 1][0] >= dp2[0][(int) nums.size() - 1][0];}
};
相关文章:

力扣 | 递归 | 区间上的动态规划 | 486. 预测赢家
文章目录 一、递归二、区间动态规划 LeetCode:486. 预测赢家 一、递归 注意到本题数据范围为 1 < n < 20 1<n<20 1<n<20,因此可以使用递归枚举选择方式,时间复杂度为 2 20 1024 ∗ 1024 1048576 1.05 1 0 6 2^{20…...

黑白格
题目描述 小杨有一个 n 行 m 列的网格图,其中每个格子要么是白色,要么是黑色。 小杨想知道至少包含 k 个黑色格子的最小子矩形包含了多少个格子。 输入格式 第一行包含三个正整数 n,m,k,含义如题面所示。 之后 n 行,每行⼀个…...

数据链路层(MAC地址)
文章目录 数据链路层(MAC地址)1、以太网2、以太网帧格式3、MAC地址4、对比理解 MAC 地址和 IP 地址5、最大传输单元(MTU)6、MTU 对 IP 协议的影响7、MTU 对 UDP 协议的影响8、MTU 对 TCP 协议的影响9、查看硬件地址和 MTU10、ARP …...

【ruby java】登陆功能/邮件发送模版240903
Rails 风格登录系统添加全面而详细的注释,解释每个部分的功能和用途。 详细注释,解释了每个文件和代码块的功能。以下是一些关键点的总结: 1. 控制器(Controllers): - ApplicationController: …...

告别格式不兼容烦恼!ape转换mp3,分享3个简单方法
各位读者们,你们是否有过这种体验:满怀期待地在网上下载一首好听的歌曲,结果怎么点击手机都播放不了,定睛一看,弹窗显示“无法播放该音频文件”。这是为什么呢?原来那首歌的音频格式是ape,不被手…...
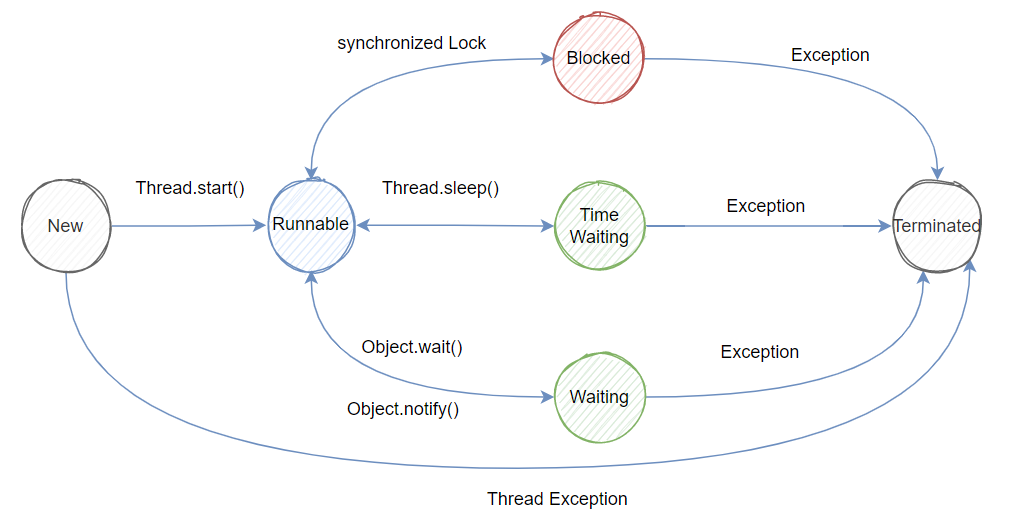
Java核心知识体系-并发与多线程:线程基础
1 先导 Java线程基础主要包含如下知识点,相信我们再面试的过程中,经常会遇到类似的提问。 1、线程有哪几种状态? 线程之间如何转变? 2、线程有哪几种实现方式? 各优缺点? 3、线程的基本操作(线程管理机制ÿ…...
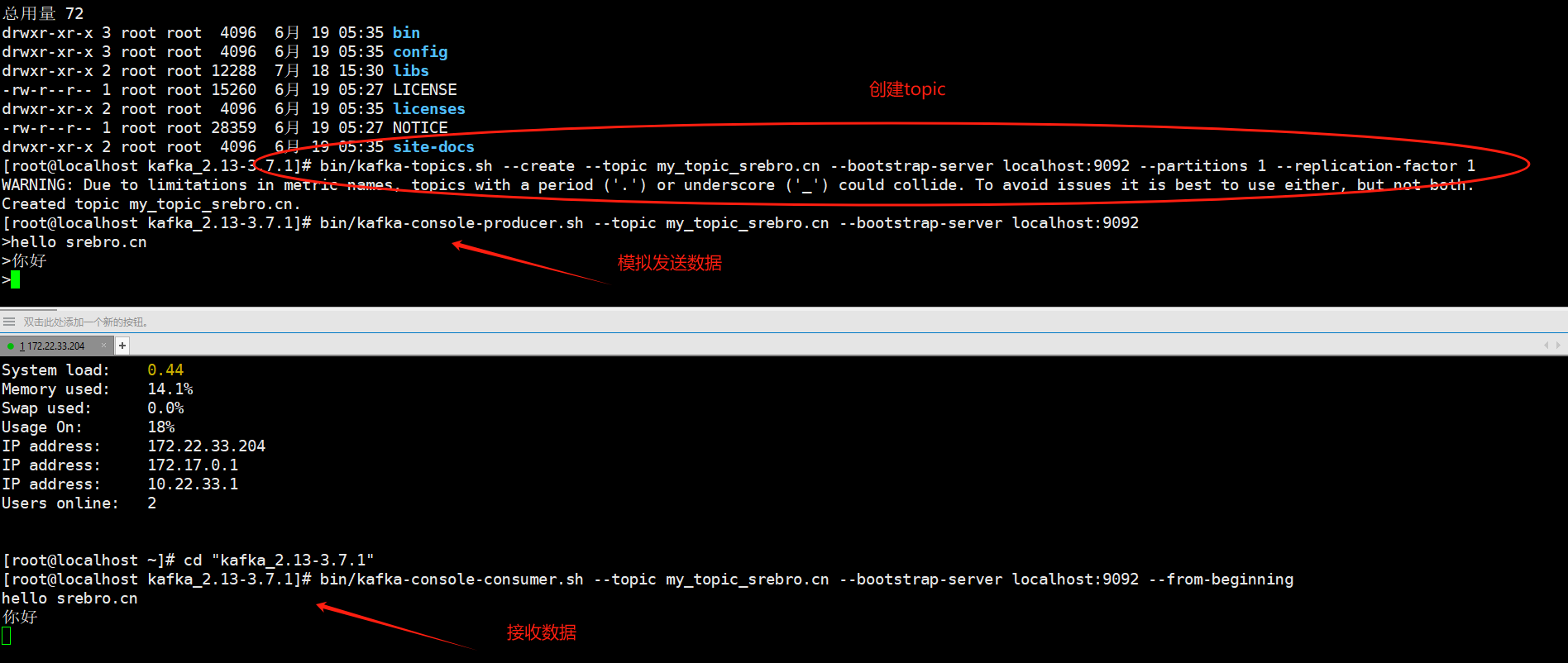
KRaft模式下的Kafka启动指南:摆脱Zookeeper依赖
一、背景介绍 多年来,人们一直在同时使用Apache ZooKeeper和Apache Kafka。但是自Apache Kafka 3.3发布以来,它就可以在没有ZooKeeper的情况下运行。同时它包含了新的命令kafka-metadata-quorum和kafka-metadata-shell?该如何安装新版kafka,…...

【数据库】MySQL-基础篇-函数
专栏文章索引:数据库 有问题可私聊:QQ:3375119339 目录 一、简介 二、字符串函数 三、数值函数 四、日期函数 五、流程函数 一、简介 函数 是指一段可以直接被另一段程序调用的程序或代码。 也就意味着,这一段程序或代码在 M…...

dp练习【4】
最长数对链 646. 最长数对链 给你一个由 n 个数对组成的数对数组 pairs ,其中 pairs[i] [lefti, righti] 且 lefti < righti 。 现在,我们定义一种 跟随 关系,当且仅当 b < c 时,数对 p2 [c, d] 才可以跟在 p1 [a, b…...

php 实现推荐算法
在PHP中实现推荐算法的应用场景通常包括电商、社交媒体、内容平台等。推荐算法可以帮助用户找到与其兴趣相关的内容,提高用户体验和平台黏性。以下是几种常见的推荐算法及其PHP实现方式: 1. 基于协同过滤的推荐算法 协同过滤(Collaborative…...
——光圈)
相机光学(三十六)——光圈
0.参考链接 (1)Hall光圈和Piris光圈的区别 (2)自动光圈及P-IRIS原理 1.光圈分类 Hall光圈和Piris光圈是两种不同的光圈技术。它们之间的区别如下: Hall光圈:Hall光圈是一种传统的光电子元件,通…...

数据结构——树和二叉树
目录 一、树的概念 二、树结点之间的关系 三、二叉树 1、满二叉树 2、完全二叉树 四、二叉树的存储 1、顺序存储 2、链式存储 一、树的概念 如果数据和数据之间满足一对多的关系,将其逻辑结构称之为树 如下图:树的根与树的分支存在一对多的关系 将上…...

142. Go操作Kafka(confluent-kafka-go库)
文章目录 Apache kafka简介开始使用Apache Kafka构建生产者构建消费者 总结 之前已经有两篇文章介绍过 Go如何操作 kafka 28.windows安装kafka,Go操作kafka示例(sarama库) 51.Go操作kafka示例(kafka-go库) Apache ka…...

spring boot(学习笔记第十九课)
spring boot(学习笔记第十九课) Spring boot的batch框架,以及Swagger3(OpenAPI)整合 学习内容: Spring boot的batch框架Spring boot的Swagger3(OpenAPI)整合 1. Spring boot batch框架 Spring Batch是什么 Spring Batch 是一个…...

docker安装 redis 并且加密开启SSL/TLS通道
拉取镜像 docker pull registry.cn-hangzhou.aliyuncs.com/qiluo-images/redis:latest docker tag registry.cn-hangzhou.aliyuncs.com/qiluo-images/redis:latest redis:latest要在 Docker 容器中启动 Redis 并开启 SSL/TLS 加密,需按照以下步骤修改启动命令和配置…...

什么是ARM架构?什么是X86架构?两者的区别是什么?
一、什么是ARM架构 (一)起源于发展 ARM 架构由英国剑桥的 Acorn 计算机公司开发。因市场无合适产品,Acorn 自行设计出第一款微处理器,命名为 ARM。此后 ARM 架构不断发展,1990 年为与苹果合作成立 ARM 公司࿰…...
【vscode】vscode paste image插件设置
本文首发于 ❄️慕雪的寒舍 vscode编辑md文件的时候,如果想插入图片,自带的粘贴只会粘贴到当前目录下,也没有文件重命名,很不友好。 在扩展商店里面有mushan的Paste Image插件,相比自带的,更加友好一点。但…...

自定义string类
#include <iostream> #include <string> int main() { std::string str "Hello, World!"; // 使用 c_str() 将 std::string 转换为 C 风格字符串,并传递给 printf printf("The string is: %s\n", str.c_str()); // 尝试修改…...

Python | Leetcode Python题解之第387题字符串中的第一个唯一字符
题目: 题解: class Solution:def firstUniqChar(self, s: str) -> int:position dict()q collections.deque()n len(s)for i, ch in enumerate(s):if ch not in position:position[ch] iq.append((s[i], i))else:position[ch] -1while q and po…...

RocketMQ 消费时序列化报错问题分析及解决
问题背景 在2024年3月7日,系统消费 RocketMQ 消息时出现了序列化报错,错误信息显示为: java.io.InvalidClassException: com.xxx.xxx.bean.mg.GoodsChangeLogMessage; local class incompatible: stream classdesc serialVersionUID... 这是…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...

Qt Quick Controls模块功能及架构
Qt Quick Controls是Qt Quick的一个附加模块,提供了一套用于构建完整用户界面的UI控件。在Qt 6.0中,这个模块经历了重大重构和改进。 一、主要功能和特点 1. 架构重构 完全重写了底层架构,与Qt Quick更紧密集成 移除了对Qt Widgets的依赖&…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
)
GitHub 常见高频问题与解决方案(实用手册)
1.Push 提示权限错误(Permission denied) 问题: Bash Permission denied (publickey) fatal: Could not read from remote repository. 原因: 没有配置 SSH key 或使用了 HTTPS 而没有权限…...

docker容器互联
1.docker可以通过网路访问 2.docker允许映射容器内应用的服务端口到本地宿主主机 3.互联机制实现多个容器间通过容器名来快速访问 一 、端口映射实现容器访问 1.从外部访问容器应用 我们先把之前的删掉吧(如果不删的话,容器就提不起来,因…...

C++ 变量和基本类型
1、变量的声明和定义 1.1、变量声明规定了变量的类型和名字。定义初次之外,还申请存储空间,也可能会为变量赋一个初始值。 如果想声明一个变量而非定义它,就在变量名前添加关键字extern,而且不要显式地初始化变量: e…...
