比较顺序3s1，3s2，4s1之间的关系
(A,B)---6*30*2---(0,1)(1,0)
分类A和B，让B全是0。当收敛误差为7e-4，收敛199次取迭代次数平均值，3s1为
3s2为
4s1为
3s1，3s2，4s1这3个顺序之间是否有什么联系 ，
因为4s1可以按照结构加法
变换成与4s1内在顺序完全相同的3点结构4s1-3，所以就是比较3s1，3s2，4s1-3之间的关系。
迭代次数实测的一组数据为
| 3s1 | 3s2 | 4s1 | ||||||
| 迭代次数 | 搜索难度 | 迭代次数 | 搜索难度 | 迭代次数 | 搜索难度 | |||
| 1 | 13381.0804 | 1 | 1 | 19694.6884 | 1 | 1 | 4202.005 | 1 |
| 2 | 27201.402 | 2.03282554 | 2 | 24311.6734 | 1.2344279 | 2 | 10464.065 | 2.4902553 |
| 3 | 26976.6181 | 2.0160269 | 3 | 25092.0955 | 1.2740539 | 3 | 12464.739 | 2.9663788 |
| 4 | 24475.6734 | 1.82912535 | 4 | 33449.2312 | 1.6983884 | 4 | 12975.07 | 3.0878284 |
| 5 | 38665.3015 | 2.88955005 | 5 | 38293.7136 | 1.9443676 | 5 | 24480.256 | 5.8258513 |
| 6 | 45053.8543 | 3.36698181 | 6 | 60504.9598 | 3.0721461 | 6 | 27187.201 | 6.4700544 |
| 7 | 27969.191 | 6.6561536 | ||||||
| 8 | 33727.322 | 8.0264829 | ||||||
| 9 | 23485.432 | 5.5891014 | ||||||
| 10 | 26175.724 | 6.2293413 | ||||||
| 11 | 27994.397 | 6.6621522 | ||||||
| 12 | 31024.709 | 7.3833107 | ||||||
| 13 | 42767.271 | 10.177825 | ||||||
| 14 | 35176.246 | 8.3713004 | ||||||
| 15 | 41257.211 | 9.8184583 | ||||||
| 16 | 55639.523 | 13.241184 |
由4s1得到4s1-3的搜索难度为
| 4s1-3 | ||
| 搜索难度 | 归一化 | |
| 1 | 4.83650101 | 1.00000021 |
| 2 | 5.77874126 | 1.19481883 |
| 3 | 5.57844875 | 1.15340613 |
| 4 | 6.98566992 | 1.44436471 |
| 5 | 7.52134055 | 1.55512055 |
| 6 | 10.3803178 | 2.14624579 |
把4s1-3和3s1，3s2的搜索难度放在一起
| 4s1-3 | 3s1 | 3s2 |
| 1.000000209 | 1 | 1 |
| 1.194818829 | 2.032825541 | 1.234427924 |
| 1.153406131 | 2.016026904 | 1.274053944 |
| 1.44436471 | 1.829125349 | 1.698388439 |
| 1.555120552 | 2.889550047 | 1.944367573 |
| 2.14624579 | 3.366981807 | 3.072146075 |
画成图
4s1-3最小，3s1最大，而3s2刚好在两条曲线的中间。
| 4s1-3 | 3s1 | 3s2 | （3s1+4s1-3）/2 |
| 1.000000209 | 1 | 1 | 1.000000104 |
| 1.194818829 | 2.032825541 | 1.234427924 | 1.613822185 |
| 1.153406131 | 2.016026904 | 1.274053944 | 1.584716517 |
| 1.44436471 | 1.829125349 | 1.698388439 | 1.63674503 |
| 1.555120552 | 2.889550047 | 1.944367573 | 2.222335299 |
| 2.14624579 | 3.366981807 | 3.072146075 | 2.756613798 |
计算4s1-3和3s1的平均值并画图
4条线画在一起
只画3s2和（3s1+4s1-3）/2两条线，尽管有误差，但（3s1+4s1-3）/2确实很接近3s2。
由此假设（3s1+4s1-3）/2=3s2，或者简写3s1+4s1=2*3s2也就是假设3s1和4s1内在顺序的平均值就是3s2.
相关文章：
比较顺序3s1，3s2，4s1之间的关系
(A,B)---6*30*2---(0,1)(1,0) 分类A和B，让B全是0。当收敛误差为7e-4，收敛199次取迭代次数平均值，3s1为 3s2为 4s1为 3s1，3s2，4s1这3个顺序之间是否有什么联系 ， 因为4s1可以按照结构加法 变换成与4s1内在…...
BUUCTF靶场[web][极客大挑战 2019]Http、[HCTF 2018]admin
目录 [web][极客大挑战 2019]Http 考点：Referer协议、UA协议、X-Forwarded-For协议 [web][HCTF 2018]admin 考点：弱密码字典爆破 四种方法： [web][极客大挑战 2019]Http 考点：Referer协议、UA协议、X-Forwarded-For协议 访问…...
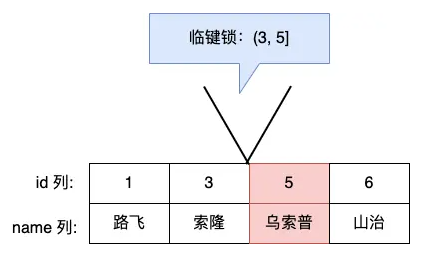
数据库锁之行级锁、记录锁、间隙锁和临键锁
1. 行级锁 InnoDB 引擎支持行级锁，而MyISAM 引擎不支持行级锁，只支持表级锁。行级锁是基于索引实现的。 对于普通的select语句，是不会加记录锁的，因为它属于快照读，通过在MVCC中的undo log版本链实现。如果要在查询时对…...
基于yolov8的血细胞检测计数系统python源码+onnx模型+评估指标曲线+精美GUI界面
【算法介绍】 基于YOLOv8的血细胞检测与计数系统是一种利用深度学习技术，特别是YOLOv8目标检测算法，实现高效、准确血细胞识别的系统。该系统能够自动识别并计数图像或视频中的血细胞，包括红细胞、白细胞和血小板等，为医疗诊断提…...
【深度学习详解】Task3 实践方法论-分类任务实践 Datawhale X 李宏毅苹果书 AI夏令营
前言 综合之前的学习内容， 本篇将探究机器学习实践方法论 出现的问题及其原因 🍎 🍎 🍎 系列文章导航 【深度学习详解】Task1 机器学习基础-线性模型 Datawhale X 李宏毅苹果书 AI夏令营 【深度学习详解】Task2 分段线性模型-引入…...
乐凡北斗 | 手持北斗智能终端的作用与应用场景
在科技日新月异的今天，北斗智能终端作为一项融合了北斗导航系统与现代智能技术的创新成果，正悄然改变着我们的生活方式和工作模式。 北斗智能终端，是以北斗卫星导航系统为核心，集成了高精度定位、导航、授时等功能的智能设备。它…...
Linux：线程互斥
线程互斥 先看到一个抢票案例： class customer { public:int _ticket_num 0;pthread_t _tid;string _name; };int g_ticket 10000;void* buyTicket(void* args) {customer* cust (customer*)args;while(true){if(g_ticket > 0){usleep(1000);cout << …...
misc流量分析
一、wireshark语法 1、wireshark过滤语法 （1）过滤IP地址 ip.srcx.x..x.x 过滤源IP地址 ip.dstx.x.x.x 过滤目的IP ip.addrx.x.x.x 过滤某个IP （2）过滤端口号 tcp.port80tcp.srcport80 显示TCP的源端口80tcp.dstport80 显示…...
Linux驱动（五）：Linux2.6驱动编写之设备树
目录 前言一、设备树是个啥？二、设备树编写语法规则1.文件类型2.设备树源文件（DTS）结构3.设备树源文件（DTS）解析 三、设备树API函数1.在内核中获取设备树节点（三种）2.获取设备树节点的属性 四、…...
算法【Java】 —— 前缀和
模板引入 一维前缀和 https://www.nowcoder.com/share/jump/9257752291725692504394 解法一：暴力枚举 在每次提供 l 与 r 的时候，都从 l 开始遍历数组，直到遇到 r 停止，这个方法的时间复杂度为 O(N * q) 解法二：前…...
python网络爬虫（四）——实战练习
0.为什么要学习网络爬虫 深度学习一般过程: 收集数据，尤其是有标签、高质量的数据是一件昂贵的工作。 爬虫的过程，就是模仿浏览器的行为，往目标站点发送请求，接收服务器的响应数据，提取需要的信息，…...
tio websocket 客户端 java 代码 工具类
为了更好地组织代码并提高可复用性，我们可以将WebSocket客户端封装成一个工具类。这样可以在多个地方方便地使用WebSocket客户端功能。以下是使用tio库实现的一个WebSocket客户端工具类。 1. 添加依赖 确保项目中添加了tio的依赖。如果使用的是Maven，可以…...
通过卷积神经网络（CNN）识别和预测手写数字
一：卷积神经网络（CNN）和手写数字识别MNIST数据集的介绍 卷积神经网络（Convolutional Neural Networks，简称CNN）是一种深度学习模型，它在图像和视频识别、分类和分割任务中表现出色。CNN通过模仿…...
【A题第二套完整论文已出】2024数模国赛A题第二套完整论文+可运行代码参考（无偿分享）
“板凳龙” 闹元宵路径速度问题 摘要 本文针对传统舞龙进行了轨迹分析，并针对一系列问题提出了解决方案，将这一运动进行了模型可视化。 针对问题一，我们首先对舞龙的螺线轨迹进行了建模，将直角坐标系转换为极坐标系࿰…...
一份热乎的数据分析(数仓)面试题 | 每天一点点，收获不止一点
目录 1. 已有ods层⽤⼾表为ods_online.user_info，有两个字段userid和age，现设计数仓⽤⼾表结构如 下： 2. 设计数据仓库的保单表（⾃⾏命名） 3. 根据上述两表，查询2024年8⽉份，每⽇，…...
3 html5之css新选择器和属性
要说css的变化那是发展比较快的，新增的选择器也很多，而且还有很多都是比较实用的。这里举出一些案例，看看你平时都是否用过。 1 新增的一些写法： 1.1 导入css 这个是非常好的一个变化。这样可以让我们将css拆分成公共部分或者多…...
【Kubernetes】K8s 的鉴权管理（一）：基于角色的访问控制（RBAC 鉴权）
K8s 的鉴权管理（一）：基于角色的访问控制（RBAC 鉴权） 1.Kubernetes 的鉴权管理1.1 审查客户端请求的属性1.2 确定请求的操作 2.基于角色的访问控制（RBAC 鉴权）2.1 基于角色的访问控制中的概念2.1…...
保研 比赛 利器： 用AI比赛助手降维打击数学建模
数学建模作为一个热门但又具有挑战性的赛道，在保研、学分加分、简历增色等方面具有独特优势。近年来，随着AI技术的发展，特别是像GPT-4模型的应用，数学建模的比赛变得不再那么“艰深”。通过利用AI比赛助手，不仅可以大大…...
秋招校招，在线性格测评应该如何应对
秋招校招，如果遇到在线测评，如何应对？ 这里写个总结稿，希望对大家有些帮助。在线测评是企业深入了解求职人的渠道，如果是性格测试，会要求测试者能够快速答出，以便于反应实际情况（时间…...
chrome 插件开发入门
1. 介绍 Chrome 插件可用于在谷歌浏览器上控制当前页面的一些操作，可自主控制网页，提升效率。 平常我们可在谷歌应用商店中下载谷歌插件来增强浏览器功能，作为开发者，我们也可以自己开发一个浏览器插件来配合我们的日常学习工作…...
python打卡day49
知识点回顾： 通道注意力模块复习空间注意力模块CBAM的定义 作业：尝试对今天的模型检查参数数目，并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略，并且实现了基本的选区操作，还调研了自绘选区的实现。那么相对的，我们还需要设计编辑器的选区表达，也可以称为模型选区。编辑器中应用变更时的操作范围，就是以模型选区为基准来…...
抖音增长新引擎：品融电商，一站式全案代运营领跑者
抖音增长新引擎：品融电商，一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中，品牌如何破浪前行？自建团队成本高、效果难控；碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...
【2025年】解决Burpsuite抓不到https包的问题
环境：windows11 burpsuite:2025.5 在抓取https网站时，burpsuite抓取不到https数据包，只显示： 解决该问题只需如下三个步骤： 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
RNN避坑指南：从数学推导到LSTM/GRU工业级部署实战流程
本文较长，建议点赞收藏，以免遗失。更多AI大模型应用开发学习视频及资料，尽在聚客AI学院。 本文全面剖析RNN核心原理，深入讲解梯度消失/爆炸问题，并通过LSTM/GRU结构实现解决方案，提供时间序列预测和文本生成…...
今日学习：Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器（ADC），支持8kHz~96kHz采样率，集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器，适用于高保真音频采集场景。 2. 核心特性 高精度：24位分辨率，…...
Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral（热门工具 Ruff 的开发者）推出的下一代高性能 Python 包管理器和构建工具，用 Rust 编写。它旨在解决传统工具（如 pip、virtualenv、pip-tools）的性能瓶颈，同时…...
#Uniapp篇：chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器：Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...