全能型 AI 的崛起:未来的市场宠儿还是昙花一现?

近日,OpenAI 宣布将在秋季推出代号为“草莓”的新一代 AI 模型。这款 AI 被描述为全能型,从处理复杂的数学问题到应对主观性强的营销策略,它的能力可以覆盖多个领域。听起来像是科技界的“万能钥匙”,无论面对什么问题,都能快速找到解决方案。
然而,这样的全能型 AI 是否真的能成为未来的主流?相比专注于某一领域、技能更精深的专业型 AI,"草莓"这样的多功能 AI 是否会更受市场欢迎?本文将通过几个简单的比喻来探讨这两种 AI 产品的优劣及其未来的市场潜力。
全能型 AI:科技界的“瑞士军刀”
我们可以把全能型 AI 比作一把瑞士军刀。它虽然不是某一个工具的顶尖选择,但无论面对哪种任务,它总能提供一种解决方案。比如,当你出门远足时,带上一把瑞士军刀是最便捷的选择,因为它有螺丝刀、剪刀、开瓶器等工具应对各种突发情况。类似地,全能型 AI 像“草莓”一样,可以在多个领域提供支持,不管是解答数学方程,还是设计营销策略,它都能找到一个合理的解决办法。
这种“瑞士军刀”式的 AI 具有广泛的应用场景。对于企业来说,使用一个能适应多种任务的 AI,可以简化流程,减少需要管理多个专门 AI 的复杂性。想象一下,作为企业管理者,你只需要与一款全能 AI 协作,就能满足财务、营销、甚至技术支持等多方面的需求。
但问题是,全能型 AI 能否在每一个领域都做到最好?毕竟,瑞士军刀虽好,但单就某一个工具而言,它远不如专用工具好用。如果你需要一把剪刀,专业的剪刀无疑比瑞士军刀上的小剪刀更锋利、效率更高。同样,在复杂的场景下,全能型 AI 可能无法提供像专业型 AI 那样精细的处理能力。
专业型 AI:精雕细琢的工具
与全能型 AI 不同,专业型 AI 更像是一个经过精细打磨的专业工具。假设你是个建筑师,你可能会选择一个能精确切割钢材的电锯,而不是一把兼具多功能的工具。专注于单一领域的 AI 拥有更深的理解和处理能力,能够在特定场景下表现出色。例如,金融预测 AI 就可能通过学习海量的市场数据,为投资者提供精准的股票走势预测;而医疗 AI 则专注于疾病诊断,通过分析复杂的医学影像帮助医生更准确地判断病情。
专业型 AI 产品的优势在于专注与精准。它们往往被设计为解决特定领域的复杂问题,具备深度学习与推理能力。虽然它们无法处理多样化的任务,但在特定领域的表现往往优于全能型 AI。因此,对于那些需要高精度处理的行业,如医疗、法律或科学研究,专业型 AI 可能依然是不可或缺的选择。
然而,专业型 AI 的缺点在于它们只能解决特定的问题,如果企业有多样化的需求,可能需要不同的专业 AI 系统。这意味着管理的复杂性增加了——就像一位厨师,虽然有最好的刀具和锅具,但却需要许多不同的设备才能应对所有料理。
全能型 vs 专业型:谁将赢得市场?
讨论到这里,全能型 AI 和专业型 AI 的优劣似乎已经很明显了。那么问题来了,未来的市场更青睐哪种 AI?
全能型 AI 无疑会有一个更广阔的用户基础。它能够为普通用户和中小型企业提供便利,因为他们可能没有足够的资源去管理多个专门的 AI 工具。这类 AI 可以帮助他们高效完成不同类型的任务,甚至节约成本。
然而,在一些要求高度专业化的领域,专业型 AI 仍然具有不可替代的价值。例如,在医疗诊断、自动驾驶、复杂科学研究等行业,高度精确和定制化的 AI 工具往往更受青睐。
我们可以打个比方:全能型 AI 更像是手机上的“备忘录”应用,你可以随时记录任何事情——购物清单、灵感、任务列表等,虽然它非常方便,但当你需要写一篇正式的论文时,你可能还是会选择一个专业的文字处理软件,如 Microsoft Word。专业型 AI 就是这类专用工具,它们提供更强大的功能,但可能不适用于日常的多样化任务。
结语:全能与专业的平衡
无论是全能型 AI 还是专业型 AI,都有各自的市场空间和应用场景。全能型 AI 适合广泛的日常任务和多样化需求,而专业型 AI 则在精细和复杂的特定领域表现出色。未来,这两类 AI 产品可能会共存,并根据用户的需求各司其职。
在市场上,全能型 AI 有潜力吸引更多的普通用户,而专业型 AI 则将继续在高度专业化的行业中发挥不可或缺的作用。那么,你更看好哪种 AI 产品的未来?不妨在评论区分享你的观点!
相关文章:

全能型 AI 的崛起:未来的市场宠儿还是昙花一现?
近日,OpenAI 宣布将在秋季推出代号为“草莓”的新一代 AI 模型。这款 AI 被描述为全能型,从处理复杂的数学问题到应对主观性强的营销策略,它的能力可以覆盖多个领域。听起来像是科技界的“万能钥匙”,无论面对什么问题,…...

如何在PPT中插入已经绘制好的excel表格数据
1、新建一个演示文稿 2、点击“插入—对象” 3、点击“由文件创建—浏览” 4、浏览选择电脑上所处理好的excel表格数据 5、这样就可将excel表格数据插入PPT中...

微积分直觉:隐含微分
目录 一、介绍 二、梯子问题 三、结论 四、一个额外的例子 一、介绍 让我们想象一个半径为 5 的圆,以 xy 平面为中心。现在假设我们想在点 (3,4) 处找到一条切线到圆的斜率。 好吧,为了做到这一点,我们必须非常接近圆和…...

Matlab自学笔记三十五:表table数据与外部文件的读入和写出
1.首先新建一个表变量t xingming{zhangsan;lisi;wangwu}; xuehao{1001;1002;1003}; chengji[89 95;90 87;88 84]; ttable(xingming,xuehao,chengji) 2.把表t的数据写出到student.txt writetable(t,student.txt) %使用writetable函数写出数据到txt文件 3.从student.txt文…...

闯关leetcode——3.Longest Substring Without Repeating Characters
大纲 题目地址内容 解题代码地址 题目 地址 https://leetcode.com/problems/longest-substring-without-repeating-characters/description/ 内容 Given a string s, find the length of the longest substring without repeating characters. Example 1: Input: s “abc…...
)
Android Radio2.0——公告注册及监听(三)
前面文章内容介绍了 Radio 相关功能的设置,我们知道可以通过设置来监听不同内容的广播公告,但是在开启对应功能的同时,还需要先注册对应公告监听,这里我们就来看一下广播公告监听的注册流程。 一、注册公告 1、接口封装 private final AtomicBoolean mHasRegisterTa = n…...

【C++】类和对象(三)再探构造函数|static成员函数|友元函数|内部类|匿名对象|对象拷贝时的编译优化
欢迎来到HarperLee的学习笔记! 一、再探构造函数 初始化列表:构造函数初始化的第二种方式(第一种是使用函数体内赋值)。使用方式:以一个冒号:开始,用逗号,分隔数据成员列表,每个成员变量后面跟…...

2024中国算力大会 2024 China Computational Power Conference
文章目录 一、会议详情二、重要信息三、大会介绍四、出席嘉宾五、征稿主题六、咨询 一、会议详情 二、重要信息 大会官网:https://ais.cn/u/vEbMBz提交检索:EI Compendex、IEEE Xplore、Scopus会议时间:2024年9月27-29日会议地点:…...

jEasyUI 扩展行显示细节
jEasyUI 扩展行显示细节 jEasyUI 是一个基于 jQuery 的前端框架,它提供了一系列的 UI 组件,使得 Web 应用的界面开发变得更加简单快捷。在 jEasyUI 的表格(datagrid)组件中,扩展行显示细节是一个常用的功能,它允许用户通过点击一行来展开更多的信息,这样可以有效地展示…...
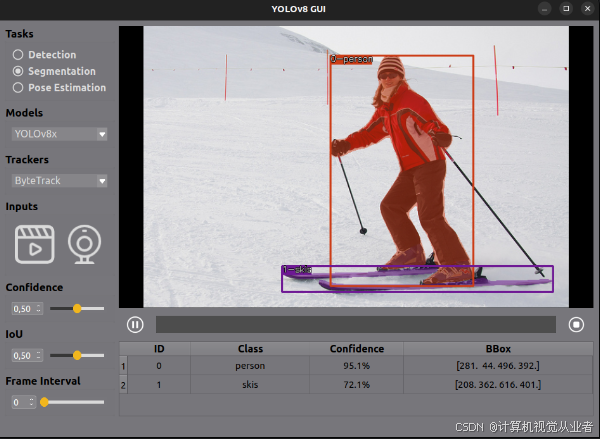
YOLOv8+Deepsort+PyQt+GUI 语义分割+目标检测+姿态识别 三者合一(集成于一套系统)综合视觉分析系统
综合视觉分析系统 技术栈: YOLOv8:用于目标检测,是一个快速且准确的目标检测框架。DeepSORT:用于目标跟踪,结合了深度学习特征提取和卡尔曼滤波器来预测目标轨迹。GUI:提供一个直观易用的图形用户界面&am…...

机器学习无监督学习
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl1. 无监督学习概述 1.1 定义与特点 无监督学习是一种数据挖掘技术,它允许机器通过观察数据来学习数据的内在结构和模式,而无需预先标注的输出变量。这种方法特别适用于数据探索和发现隐藏在数据…...

windows10-VMware17-Ubuntu-22.04-海康2K摄像头兼容问题,求解(已解决)
文章目录 1.webrtc camera测试2.ffmpeg 测试3.Ubuntu 自带相机4.解决办法 环境:windows10系统下,VMware的Ubuntu-22.04系统 问题:摄像头出现兼容问题,本来是想开发测试的,Ubuntu方便些。买了海康2K的USB摄像头…...

【系统架构设计师】解释器模式
解释器模式(Interpreter Pattern)是一种行为型设计模式,它定义了文法的表示,并定义了一个解释器,该解释器使用该表示来解释语言中的句子。在解释器模式中,通常包括一个抽象语法树(Abstract Synt…...

Hive原理剖析
1. 概述 背景介绍 Apache Hive是一个基于Hadoop的开源数据仓库软件,为分析和管理大量数据集提供了SQL-like的接口。最初由Facebook开发并贡献给Apache,Hive现已成为大数据处理领域的重要工具之一。它将传统的SQL功能与Hadoop的强大分布式处理能力结合&…...

在 Ubuntu 上查看重复文件
一般情况下 1. 使用 fdupes 工具 fdupes 是一个专门用于查找重复文件的工具。 安装: sudo apt-get install fdupes 使用: fdupes -r /path/to/directory -r 选项会递归查找子目录中的重复文件。 2. 使用 rmlint 工具 rmlint 是另一个强大的重复文件查找工具…...

docker容器高效连接 Redis 的方式
在微服务架构中,Redis 是一种常见的高效缓存解决方案,通常用于存储临时数据、会话信息或 token。如何在服务容器中高效、稳定地连接 Redis 是架构设计中的一个重要环节。 这篇博客将以实际项目为例,详细介绍如何配置 Flask 应用中的服务容器…...

手撕Python之生成器、装饰器、异常
1.生成器 生成器的定义方式:在函数中使用yield yield值:将值返回到调用处 我们需要使用next()进行获取yield的返回值 yield的使用以及生成器函数的返回的接收next() def test():yield 1,2,3ttest() print(t) #<generator object test at 0x01B77…...

LabVIEW步进电机控制方式
在LabVIEW中控制步进电机可以通过多种方式实现。每种方法都有其独特的优缺点,适用于不同的应用场合。下面详细介绍几种常见的步进电机控制方式,并进行比较。 1. 开环控制(Open-Loop Control) 特点 通过定期发出脉冲信号来控制步进…...

vllm源码解析(五):LLM模型推理
八 模型推理细节探索 8.1 回顾下step的流程 def step(self) -> List[Union[RequestOutput, EmbeddingRequestOutput]]:# 多GPU并行推理时走AsyncLLMEngine分支。如果进入当前LLMEngine,性能会下降,这里会抛出异常。if self.parallel_config.pipeline_parallel_s…...
数学建模笔记——熵权法(客观赋权法)
数学建模笔记——熵权法[客观赋权法] 熵权法(客观赋权法)1. 基本概念2. 基本步骤3. 典型例题3.1 正向化矩阵3.2 对正向化矩阵进行矩阵标准化3.3 计算概率矩阵P3.4 计算熵权3.5 计算得分 4. python代码实现 熵权法(客观赋权法) 1. 基本概念 熵权法,物理学名词,按照信息论基本原…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
