9.9日记录
1.常见排序算法的复杂度
1.快速排序

1.1快速排序为什么快
从名称上就能看出,快速排序在效率方面应该具有一定的优势。尽管快速排序的平均时间复杂度与“归并排序”和“堆排序”相同,但通常快速排序的效率更高,主要有以下原因。
- 出现最差情况的概率很低:虽然快速排序的最差时间复杂度为 O(N的平方) ,没有归并排序稳定,但在绝大多数情况下,快速排序能在 O(nlogN) 的时间复杂度下运行。
- 缓存使用效率高:在执行哨兵划分操作时,系统可将整个子数组加载到缓存,因此访问元素的效率较高。而像“堆排序”这类算法需要跳跃式访问元素,从而缺乏这一特性。
- 复杂度的常数系数小:在上述三种算法中,快速排序的比较、赋值、交换等操作的总数量最少。这与“插入排序”比“冒泡排序”更快的原因类似。
1.2基准数优化
快速排序在某些输入下的时间效率可能降低。举一个极端例子,假设输入数组是完全倒序的,由于我们选择最左端元素作为基准数,那么在哨兵划分完成后,基准数被交换至数组最右端,导致左子数组长度为n-1,右子数组长度为0, 如此递归下去,每轮哨兵划分后都有一个子数组的长度为0,分治策略失效,快速排序退化为“冒泡排序”的近似形式。
为了尽量避免这种情况发生,我们可以优化哨兵划分中的基准数的选取策略。例如,我们可以随机选取一个元素作为基准数。然而,如果运气不佳,每次都选到不理想的基准数,效率仍然不尽如人意。
需要注意的是,编程语言通常生成的是“伪随机数”。如果我们针对伪随机数序列构建一个特定的测试样例,那么快速排序的效率仍然可能劣化。
为了进一步改进,我们可以在数组中选取三个候选元素(通常为数组的首、尾、中点元素),并将这三个候选元素的中位数作为基准数。这样一来,基准数“既不太小也不太大”的概率将大幅提升。当然,我们还可以选取更多候选元素,以进一步提高算法的稳健性。采用这种方法后,时间复杂度劣化至O(N)方 的概率大大降低。
2.冒泡排序

3.选择排序
void selectNum(vector<int>& nums) {//选择排序时间复杂度O(N)的平方 空间复杂度01int n = nums.size();for (int i = 0; i < n-1; i++) {int k = i;//用k记录未排序区间的最小元素for (int j = i + 1; j < n; j++) {if (nums[j] < nums[k]) {k = j;}}swap(nums[i],nums[k]);}
}

4.插入排序
void insertSort(vector<int>& nums) {//外循环for (int i = 1; i < nums.size(); i++) {//内循环 int base = nums[i];int j = i - 1;while (j>=0&&nums[j] > base) {nums[j + 1] = nums[j];j--;}nums[j + 1] = base;}
}
5.归并排序:
void merge(vector<int>& nums, int num1[], int left, int right,int mid){//合并int l_pos = left;//左半区int r_pos = mid + 1;//右半区int pos = left;//临时存储的数组while(l_pos<=mid&&r_pos<=right) {if (nums[l_pos] < nums[r_pos]) {num1[pos++] = nums[l_pos++];}else {num1[pos++] = nums[r_pos++];}}//合并剩余的左半区while (l_pos <= mid) {num1[pos++] = nums[l_pos++];}//合并剩余的右半区while (r_pos <=right) {num1[pos++] = nums[r_pos++];}while (left <= right) {//最后 将临时数组中的元素拷贝到目标数组中nums[left] = num1[left];left++;}
}
void msort(vector<int>& nums,int num1[],int left,int right) {//分治if (left < right) {int mid = (left + right) / 2;msort(nums,num1,left,mid);msort(nums, num1, mid + 1, right);merge(nums,num1,left,right,mid);}
}
void merge_sort(vector<int> &nums) {//入口函数int* num1 = (int*)malloc(nums.size()*sizeof(int));if (num1) {msort(nums,num1,0,nums.size()-1);free(num1);}
}

2.leetCode.58最后一个单词的长度
给你一个字符串
s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
双指针yyds,一个指针指向最后一个字符串的最后一个字符,另一个指针指向第一个,相减即可。
class Solution {
public:int lengthOfLastWord(string s) {int i=s.size()-1;while(s[i]==' '){i--;}int j=i-1;while(j>=0&&s[j]!=' '){j--;}return i-j;}
};相关文章:

9.9日记录
1.常见排序算法的复杂度 1.快速排序 1.1快速排序为什么快 从名称上就能看出,快速排序在效率方面应该具有一定的优势。尽管快速排序的平均时间复杂度与“归并排序”和“堆排序”相同,但通常快速排序的效率更高,主要有以下原因。 出现最差情况…...
鸿蒙交互事件开发04——手势事件
1 概 述 手势事件是移动应用开发中最常见的事件之一,鸿蒙提供了一些方法来绑定手势事件。通过给各个组件绑定不同的手势事件,并设计事件的响应方式,当手势识别成功时,ArkUI框架将通过事件回调通知组件手势识别的结果。 …...

研1日记9
1.理解conv1d和conv2d a. 1和2处理的数据不同,1维数据和图像 b. 例如x输入形状为(32,19,512)时,卷积公式是针对512的,而19应该变换为参数中指定的输出通道。 2.“SE块”(Squeeze-and-Excitation Block)它可以帮助模…...

HAL库学习目录查询表
日期内容2024.09.11基于STM32C8T6的CubeMX:HAL库点亮LED2024.09.11STMCuBeMX新建项目的两种匪夷所思的问题2024.09.11STMCubeMX文件下载后会出现其他项目无法下载的问题...

pandas DataFrame日期字段数据处理
pandas DataFrame日期字段数据处理 1、pandas读取表格文件日期字段存入数据库不需要时分秒 在使用 pandas 读取表格文件,并将日期字段存入数据库时,如果你只关心日期部分而不需要时分秒,可以通过以下步骤来处理: 读取数据并转换日期字段: 首先,你需要读取你的数据,并确…...

swift:qwen2 VL 多模态图文模型lora微调swift
参考: https://swift.readthedocs.io/zh-cn/latest/Multi-Modal/qwen2-vl%E6%9C%80%E4%BD%B3%E5%AE%9E%E8%B7%B5.html 在线demo: https://colab.research.google.com/drive/16yl6Z0wxHLX3qJ5q-SIbvPn251k3r2JC?usp=sharing 安装: !git clone https://github.com/modelsc…...

Vue.js中computed的使用方法
在Vue.js中,computed 属性是基于它们的依赖进行缓存的响应式属性。只有当相关依赖发生改变时,才会重新求值。这意味着只要computed属性依赖的源数据(如data中的属性)没有发生变化,多次访问computed属性会立即返回之前的…...

python之pyecharts制作可视化数据大屏
文章目录 前言一、安装 Pyecharts二、创建 Pyecharts 图表三、设计大屏布局四、实时数据更新五、部署和展示总结前言 使用 Pyecharts 制作可视化数据大屏是一个复杂但有趣的过程,因为 Pyecharts 本身是一个用于生成 Echarts 图表的 Python 库,而 Echarts 是由百度开发的一个…...

Chrome、Edge、360及Firefox浏览器加载多个ActiveX插件的介绍
allWebPlugin简介 allWebPlugin中间件是一款为用户提供安全、可靠、便捷的浏览器插件服务的中间件产品,致力于将浏览器插件重新应用到所有浏览器。它将现有ActiveX控件直接嵌入浏览器,实现插件加载、界面显示、接口调用、事件回调等。支持Chrome、Firefo…...

裸金属服务器与云服务器的区别有哪些?
随着云计算服务的快速发展,云服务器与裸金属服务器则称为各大企业基础设施的两大核心选择,会运用在不同的场景当中,本文就来介绍一下裸金属服务器与云服务器的区别都有哪些吧! 裸金属服务器相对于云服务器来说有着卓越的性能&…...

Pr:序列设置 - VR 视频
在“新建序列”对话框的“VR 视频” VR Video选项卡,或者在“序列设置”对话框的“VR 属性” VR Properties选项卡中,允许用户创建和编辑虚拟现实 (VR) 视频序列。 VR 视频能够提供 360 沉浸式的观看体验,通常使用专门的相机进行拍摄…...

采用qt做一个命令行终端
qt做一个类似系统命令行终端的工具,方便集成到自己的软件里使用,这样能保证软件的整体性,而且是真正的做到和系统命令行终端一样的交互方式,而不是单独搞个编辑框的方式输入命令(大部分博客都是做成这个样子࿰…...

TQA相关
ReAct Prompting: 原理、实现与应用 ReAct Prompting(推理与行动提示)是一种引导大型语言模型(LLM)进行推理和行动的策略,广泛应用于复杂问题求解、对话生成和自动化任务等领域。ReAct Prompting 通过将模型的思考过程…...

Spring Cloud之二 微服务注册
1:Intellij 新建服务 user-service 2:pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"…...

[Web安全 网络安全]-文件上传漏洞
文章目录: 一:前言 1.什么是文件上传漏洞 2.环境 2.1 靶场 2.2 其他工具 3.木马分类 二:文件上传分类 1.客户端 JS绕过 2.服务端-黑名单 大小写绕过 点和空格绕过 .htaccess文件绕过 php345文件绕过 windows ::$DATA绕过 3.…...

【白话Redis】缓存雪崩、穿透、击穿、失效和热点缓存重建
快速导航 Redis不可不知的故障现象一、缓存雪崩定义:解决方案: 二、缓存穿透定义:解决方案一:解决方案二(更普遍的做法): 三、缓存击穿定义:解决方案: 四、缓存失效Redis…...

flink增量检查点降低状态依赖实现的详细步骤
增量检查点启动恢复的时间是很久的,业务上不能接受,所以可以通过降低状态依赖来减少恢复的时间。 降低状态依赖 尽可能减少状态的复杂性和依赖关系,通过拆分状态或将状态外部化到其他服务中,从而降低恢复的开销。 实施措施&…...

Redis总结,是什么,干什么,怎么利用?
Redis(Remote Dictionary Server)是一个开源的内存数据库,遵守 BSD 协议,它提供了一个高性能的键值(key-value)存储系统,常用于缓存、消息队列、会话存储等应用场景 Redis主要特性 (…...

Vue3状态管理Pinia
Vue3 的 Pinia 使用指南 Pinia 是 Vue3 中官方推荐的状态管理库,作为 Vuex 的替代品,它更简洁易用,并且支持模块化、类型推断和 DevTools 集成。Pinia 非常适合在 Vue3 项目中管理全局状态。 1. 安装 Pinia 首先,我们需要在 Vu…...

box64 安装
ARM运行x86程序 docker安装 box64 安装方法 docker run --name a001 -itd --networkhost -v /www/wwwroot/docker/Box64/f:/f ubuntu:22.04 /bin/bash docker exec -it a001 bash cd /home //创建目录qq547176052 mkdir -p qq547176052 cd /home/qq547176052 apt update apt …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...
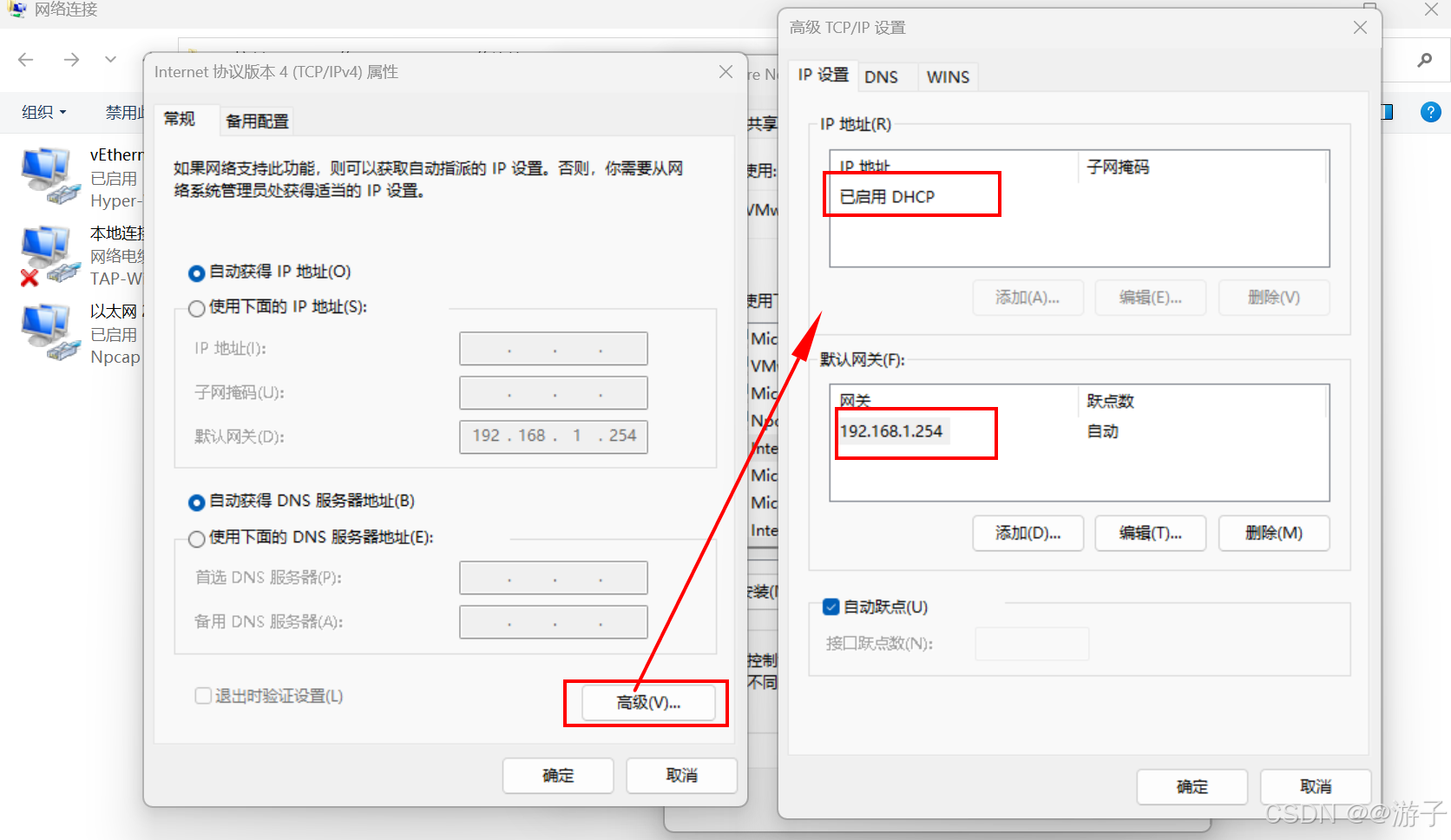
虚拟机网络不通的问题(这里以win10的问题为主,模式NAT)
当我们网关配置好了,DNS也配置好了,最后在虚拟机里还是无法访问百度的网址。 第一种情况: 我们先考虑一下,网关的IP是否和虚拟机编辑器里的IP一样不,如果不一样需要更改一下,因为我们访问百度需要从物理机…...

Ubuntu 可执行程序自启动方法
使用 autostart(适用于桌面环境) 适用于 GNOME/KDE 桌面环境(如 Ubuntu 图形界面) 1. 创建 .desktop 文件 sudo vi ~/.config/autostart/my_laser.desktop[Desktop Entry] TypeApplication NameMy Laser Program Execbash -c &…...
