【基础算法总结】位运算
目录
- 一,常见位运算操作总结
- 二,算法原理和代码实现
- 191.位1的个数
- 338.比特位计数
- 461.汉明距离
- 面试题01.01.判断字符是否唯一
- 268.丢失的数字
- 371.两整数之和
- 136.只出现一次的数字
- 137.只出现一次的数字II
- 260.只出现一次的数据III
- 面试题17.19.消失的两个数字
- 三,算法总结
一,常见位运算操作总结
1. 基础位运算符

注意:参与位运算的对象只能是整型数据(int, unsigned, char),不能为实型。
上面六种基础位运算是本篇文章重点涉及的,要想详细了解它们的含义和运算规律,请点击文章:【移位操作符,位操作符运算规则详解】
2. 位运算符的优先级

只要记住一句话:表格不用死记,能加括号就加括号。
3. 给定一个数 n ,判断他的二进制表示的第 x 位是 0 还是 1?
(n >> x) & 1
4. 将一个数 n 的二进制表示的第 x 位修改成 1
n |= (1 << x)
5. 将一个数 n 的二进制表示的第 x 位修改成 0
n &= (~(1 << x))
6. 位图思想
位图的本质是哈希表,是一个用二进制比特位表示数据是否存在的数据结构。
想详细了解什么是位图以及位图的使用,请点击文章:【哈希的应用 – 位图&布隆过滤器】
7. 提取一个数(n)二进制表示中最右侧的 1
n & -n

8. 干掉一个数(n)二进制表示中最右侧的 1
n & (n - 1)

9. 异或(^)运算的运算律

二,算法原理和代码实现
191.位1的个数


算法原理:
根据上面总结的位运算的操作,这道题有两种解法。
代码实现1:
根据上面的第三点,可以判断 n 的二进制里的每一位是否是1,如果是,计数器++。
class Solution
{
public:int hammingWeight(int n){int count = 0;for (int i = 0; i < 32; i++){if ((n >> i) & 1) count++;}return count;}
};
代码实现2:
根据上面的第8点,每次都干掉数 n 的最右侧的1,统计执行的次数即可。
class Solution {
public:int hammingWeight(int n) {int count = 0;while (n){n &= (n - 1);count++;}return count;}
};
338.比特位计数


算法原理:
这道题就是上一题的进阶题,算法原理同上,加一个循环遍历从0到n的数字,分别计算出每个数字的二进制中1的个数,存入数组中即可。
代码实现:
class Solution
{
public:vector<int> countBits(int n) {vector<int> ret;for(int i = 0; i <= n; i++){int tmp = i;unsigned int count = 0;while(tmp){tmp &= (tmp-1);count++;}ret.push_back(count);}return ret;}
};
461.汉明距离


算法原理:
根据上面的操作三,判断这两个数的每一位是否相等,如果不相等,计数器++ 即可。
代码实现:
class Solution
{
public:int hammingDistance(int x, int y) {int i = 0;int count = 0;for(; i < 32; i++)if(((x >> i) & 1) != ((y >> i) & 1)) count++;return count;}
};
面试题01.01.判断字符是否唯一


算法原理:
这道题比较简单,有多种解法:一是使用位图思想,二是使用哈希表,三是用数组模拟哈希。
这里介绍位图思想。
用一个 int 变量的32个比特位(实际上只使用26个)来标记这个字符在或不在,0 表示不在,1 表示在。
所以先要判断二进制中的第 n 位是 1 还是 0,如果是 0,就修改成 1,如果已经是 1 了,说明这个字符就已经存在了,返回false。
这里还有一个小的优化点:
由鸽巢原理(抽屉原理)可知,当字符串的长度大于26个时,一定会出现重复字符。
代码实现1:使用位图思想
class Solution
{
public:bool isUnique(string astr){if(astr.size() > 26) return false;int bitMap = 0;for (auto ch : astr){int i = ch - 'a'; // 移动的位数// 字符不存在,映射位置的比特位修改成1if (((bitMap >> i) & 1) == 0) bitMap |= (1 << i);else return false;}return true;}
};
代码实现2:使用哈希表
时间复杂度:O(N)
空间复杂度:O(N)
class Solution
{
public:bool isUnique(string astr){if(astr.size() > 26) return false;unordered_map<char, int> hash;for (auto ch : astr){// 判断是否存在if (hash.count(ch) == 0) hash[ch]++;else return false;}return true;}
};
代码实现3:用数组模拟哈希
class Solution
{
public:bool isUnique(string astr){if(astr.size() > 26) return false;int hash[26] = { 0 };for (auto ch : astr){if (hash[ch - 'a'] == 0) hash[ch - 'a']++;else return false;}return true;}
};
268.丢失的数字


算法原理:
这道题其实和 [二分查找] 系列中的最后一题是一模一样的,题目简单,解法多种。
这里介绍使用位运算。
使用异或运算的规律:
a ^ 0 = a
a ^ a = 0
a ^ b ^ c = a ^ (b ^ c)
可以先把完整的 [0, n] 共 n + 1 个数进行异或,再把这个异或结果异或上题目所给的数据,相同数异或变成0,最后剩下的那个就是缺失的数字。
代码实现:
class Solution
{
public:int missingNumber(vector<int>& nums) {int ret = 0;for(int i = 0; i <= nums.size(); i++)ret ^= i;for(auto x : nums)ret ^= x;return ret;}
};
如果想要了解其他解法,请点击文章:【二分查找】里的最后一题 [LCR173.点名]。
371.两整数之和


算法原理:
这道题使用异或运算 – 无进位相加。
先算出无进位相加的结果,再算出进位,再把两者相加,但是不能使用加法,要重复执行上面两个操作,直到进位为 0 为止。
代码实现:
class Solution
{
public:int getSum(int a, int b) {int tmp = a ^ b; // 无进位相加的结果int res = (a & b) << 1; // 算出进位// 当进位不为0时,重复上面操作while(res){a = tmp;b = res;tmp = a ^ b;res = (a & b) << 1;}return tmp;}
};
136.只出现一次的数字


算法原理:
这道题很简单,就是对异或运算律(a ^ a = 0)的简单使用。
代码实现:
class Solution
{
public:int singleNumber(vector<int>& nums) {int ret = 0;for(auto x : nums)ret ^= x;return ret;}
};
137.只出现一次的数字II


算法原理:
把所有数据的第 i 个二进制位相加,和会出现下面4种情况:
用相加的和取模3(%3),如果是三个相同的数,它们的第 i 个二进制位相加结果模3为 0,如果等于 1,说明这个二进制位是那个只出现一次的数的,就把它映射到另一个 int 变量的对应的二进制位上。
代码实现:
class Solution
{
public:int singleNumber(vector<int>& nums) {int ret = 0;for(int i = 0; i < 32; i++){int sum = 0;for(auto x : nums)sum += ((x >> i) & 1); // 把所有数字的第i个二进制位相加// 如果等于1,说明是出现一次的,把1映射到相应的二进制位if(sum % 3 != 0) ret |= (1 << i); }return ret;}
};
260.只出现一次的数据III


算法原理:
其实根据 [136.只出现一次的数字] 对这道题是有思路的,就是相同的数异或在一起就变成0了,关键就是如何把相同的数放到一组?
代码实现:
class Solution
{
public:vector<int> singleNumber(vector<int>& nums) {int tmp = 0;// 把所有数据异或在一起for(auto x : nums)tmp ^= x;// 找出tmp中,比特位上为1的位置int i = 0;for(; i < 32; i++)if((tmp >> i) & 1) break;// 根据i的位置把数据分成两类,分别异或int a = 0, b = 0;for(auto x : nums)if((x >> i) & 1) a ^= x;else b ^= x;return {a, b};}
};
面试题17.19.消失的两个数字


算法原理:
这道题本质上是 [268.消失的数字] 和 [260.只出现一次的数字III] 的结合题。

代码实现:
class Solution
{
public:vector<int> missingTwo(vector<int>& nums) {int tmp = 0;// 把所属异或在一起for(auto x : nums) tmp ^= x;for(int k = 1; k <= nums.size()+2; k++) tmp ^= k;// 找到tmp中,比特位上为1的那一位int i = 0;for(; i < 32; i++)if((tmp >> i) & 1) break;// 根据第i位的不同,把所有数据分成两类int a = 0, b = 0;for(auto x : nums)if((x >> i) & 1) a ^= x;else b ^= x;for(int j = 1 ; j <= nums.size()+2; j++)if((j >> i) & 1) a ^= j;else b ^= j;return {a, b};}
};
三,算法总结
熟练使用位运算的操作即可。
相关文章:

【基础算法总结】位运算
目录 一,常见位运算操作总结二,算法原理和代码实现191.位1的个数338.比特位计数461.汉明距离面试题01.01.判断字符是否唯一268.丢失的数字371.两整数之和136.只出现一次的数字137.只出现一次的数字II260.只出现一次的数据III面试题17.19.消失的两个数字 …...

组件通信——provide 和 inject 实现爷孙组件通信
provide 和 inject 实现爷孙组件通信 介绍 provide 和 inject 是 Vue.js 提供的一种在组件之间共享数据的机制,它允许在组件树中的任何地方注入依赖项。这对于跨越多个层级的组件间通信特别有用,因此无需手动将 prop 数据逐层传递下去。 provide&#…...

【ShuQiHere】探索人工智能核心:机器学习的奥秘
【ShuQiHere】 💡 什么是机器学习? 机器学习(Machine Learning, ML)是人工智能(Artificial Intelligence, AI)中最关键的组成部分之一。它使得计算机不仅能够处理数据,还能从数据中学习&#x…...

LeeCode打卡第二十四天
LeeCode打卡第二十四天 第一题:对称二叉树(LeeCode第101题): 给你一个二叉树的根节点 root , 检查它是否轴对称。 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* …...

什么是科技与艺术相结合的异形创意圆形(饼/盘)LED显示屏
在当今数字化与创意并重的时代,科技与艺术的融合已成为推动社会进步与文化创新的重要力量。其中,晶锐创显异形创意圆形LED显示屏作为这一趋势下的杰出代表,不仅打破了传统显示设备的形态束缚,更以其独特的造型、卓越的显示效果和广…...

AI大模型知识点大梳理_ai大模型知识学习,零基础入门到精通,收藏这一篇就够了
文章目录 AI大模型是什么AI大模型发展历程AI大模型的底层原理AI大模型解决的问题大模型的优点和不足影响个人观点 AI大模型是什么 AI大模型是指具有巨大参数量的深度学习模型,通常包含数十亿甚至数万亿个参数。这些模型可以通过学习大量的数据来提高预测能力&…...

NVG040W语音芯片:为制氧机带来个性化语音提示和报警功能
在当今社会,家庭医疗设备和健康保健产品越来越受到人们的关注。制氧机作为其中的一种,为许多需要氧气治疗的人们提供了重要的帮助。然而,对于许多用户来说,如何正确操作和维护这些设备仍然是一个挑战。为此,NVG040W语音…...

OpenCV结构分析与形状描述符(12)椭圆拟合函数fitEllipseAMS()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 围绕一组2D点拟合一个椭圆。 该函数计算出一个椭圆,该椭圆拟合一组2D点。它返回一个内切于该椭圆的旋转矩形。使用了由[260]提出的近…...

安卓显示驱动
安卓显示驱动是用于在Android设备上提供图形和视频显示的底层软件组件。 显示驱动在Android系统中扮演着至关重要的角色,它们负责将图形和视频内容从系统内存传输到显示屏上。这些驱动程序确保了用户界面、图像、视频和游戏等视觉元素的正常显示。以下是关于安卓显…...
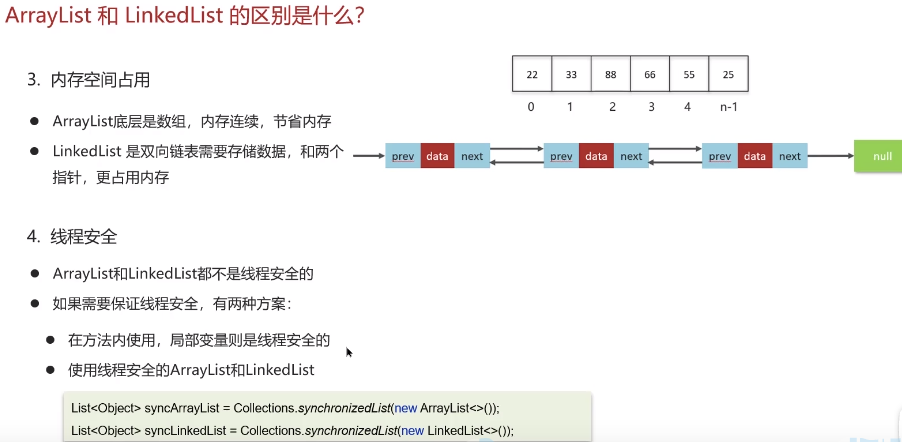
java重点学习-集合(List)
七 集合(List) 7.1 复杂度分析 7.2 数组 1.数组(Array)是一种用连续的内存空间存储相同数据类型 数据的线性数据结构。 2.数组下标为什么从0开始 寻址公式是:baseAddressi*dataTypeSize,计算下标的内存地址效率较高 3.查找的时间复杂度 随机(…...

【PCB测试】最常见的PCB测试方法
系列文章目录 1.元件基础 2.电路设计 3.PCB设计 4.元件焊接 5.板子调试 6.程序设计 7.算法学习 8.编写exe 9.检测标准 10.项目举例 11.职业规划 文章目录 一、PCB测试的好处1.发现错误2.降低成本3.节省时间4.减少退货率5.提高安全性 二、PCB测试内容1.孔壁质量2.电镀铜3.清…...
)
AtCoder Beginner Contest 370 ABCD题详细题解(C++,Python)
前言: 本文为AtCoder Beginner Contest 370 ABCD题的详细题解,包含C,Python语言描述,觉得有帮助或者写的不错可以点个赞 个人感觉D比C简单,C那里的字典序有点不理解, E应该是前缀和加dp,但是是dp不明白,等我明白了会更…...

斯坦福研究人员探讨大型语言模型在社交网络生成中的应用及其在政治同质性上的偏见
社交网络生成在许多领域有着广泛的应用,比如流行病建模、社交媒体模拟以及理解社交现象如两极化等。当由于隐私问题或其他限制无法直接观察真实网络时,创建逼真的社交网络就显得尤为重要。这些生成的网络对于在这些情况下准确建模互动和预测结果至关重要…...

一招教你找到Facebook广告的最佳发帖时间
在社交媒体上做广告时,时机是至关重要的。有时候你投放的广告参与度低,很有可能是因为你没有在适当的时机投放广告。这篇文章会教你如何找到适合自己的广告投放时间,如果你感兴趣的话,就继续看下去吧! 首先࿰…...

【数据库】MySQL-基础篇-多表查询
专栏文章索引:数据库 有问题可私聊:QQ:3375119339 目录 一、多表关系 1.一对多 2.多对多 3.一对一 二、多表查询概述 1.数据准备 2.概述 3.分类 三、内连接 1.隐式内连接 2.显式内连接 3.案例 四、外连接 1.左外连接 2.右外连…...

MongoDB事务机制
事务机制 1.事务概念 在对数据的操作的过程中,涉及到一连串的操作,这些操作如果失败,会导致我们的数据部分变化了,部分没变化。这个过程就好比如你去吃早餐,你点完餐了,并且吃完早餐了,没付钱你…...

大模型 LLM(Large Language Models)如今十分火爆,对于初入此领域的新人小白来说,应该如何入门 LLM 呢?是否有值得推荐的入门教程呢?
前言 很明显,这是一个偏学术方向的指南要求,所以我会把整个LLM应用的从数学到编程语言,从框架到常用模型的学习方法,给你捋一个通透。也可能是不爱学习的劝退文。 通常要达到熟练的进行LLM相关的学术研究与开发,至少…...

Python实现模糊逻辑算法
博客目录 引言 什么是模糊逻辑?模糊逻辑的应用场景模糊逻辑的基本思想 模糊逻辑的原理 模糊集合与隶属函数模糊推理系统(FIS)模糊规则和推理过程 Python实现模糊逻辑算法 面向对象的设计思路代码实现示例与解释 模糊逻辑算法应用实例&…...

MATLAB、FPGA、STM32中调用FFT计算频率、幅值及相位差
系列文章目录 文章目录 系列文章目录前言MATLABSTM32调用DSPSTM32中实现FFT关于初相位 FPGA 前言 最近在学习如何在STM32中调用FFT MATLAB 首先对FFT进行一下说明,我们输入N个点的数据到FFT中,FFT会返回N个点的数据,这些数据都是复数&#…...

基于SSM的医院药品库存系统的设计与实现---附源码76620
摘要 医院药品库存管理是医院管理的重要组成部分,对于保障医疗服务的质量和效率具有重要意义。传统的手工管理方式已经无法满足药品库存管理的需求,因此建立一个医院药品库存系统具有重要的实践价值。 使用Java语言开发医院药品库存系统可以兼容不同操作…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...




