算法详解-双指针算法的魅力-一种简单而高效的编程思想
文章目录
- 双指针简介
- 快慢指针
- 快慢指针介绍
- 快慢指针例题
- 快慢指针优缺点:
- 对撞指针
- 对撞指针介绍:
- 对撞指针例题
- 对撞指针优缺点:
- 更新中——未完
- 总结
- 更多宝藏
双指针简介
😎🥳😎🤠😮🤖🙈💭🍳🍱
双指针算法是一种通过设置两个指针不断进行单向移动来解决问题的算法。
它包含两种形式:快慢指针和对撞指针。
快慢指针是一种设置步长不同的两个指针,用于解决链表中的问题,如判断是否有环,找到中间节点等。
对撞指针是一种设置在序列两端向中间移动的两个指针,用于解决数组中的问题,如找到两数之和,反转元音字母等。
双指针算法的核心思想是利用单调性或者有序性,减少不必要的遍历,优化时间复杂度。下面我们将分别介绍这两种形式的双指针算法,并给出一些例题和解析。
快慢指针
🦞🦐🦀🦑🦪
快慢指针介绍
快慢指针是一种设置步长不同的两个指针,用于解决链表中的问题,如判断是否有环,找到中间节点等。
快慢指针的基本思想是让一个指针每次移动一步,另一个指针每次移动两步,这样当两个指针相遇时,就可以得到一些有用的信息。下面我们将通过一些例题来展示快慢指针的用法和技巧。
快慢指针例题
例题1:判断链表是否有环
给定一个链表,判断链表中是否有环。如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。
思路:我们可以使用快慢指针来解决这个问题。首先,我们定义两个指针 fast 和 slow ,并让它们都指向链表的头节点。然后,我们让 fast 每次移动两个节点,slow 每次移动一个节点。如果链表中没有环,那么 fast 最终会遇到空节点,结束循环。如果链表中有环,那么 fast 和 slow 最终会在环内相遇,也结束循环。我们只需要判断循环结束时 fast 和 slow 是否相等,就可以知道链表是否有环。
代码:
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) {
return false;
}
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
return true;
}
}
return false;
}
例题2:找到链表的中间节点
给定一个头结点为 head 的非空单链表,返回链表的中间结点。如果有两个中间结点,则返回第二个中间结点。
思路:我们可以使用快慢指针来解决这个问题。首先,我们定义两个指针 fast 和 slow ,并让它们都指向链表的头节点。然后,我们让 fast 每次移动两个节点,slow 每次移动一个节点。当 fast 到达链表的末尾时,slow 就恰好在链表的中间节点。如果链表的长度是偶数,那么 fast 会停在最后一个节点的后面,此时 slow 在中间两个节点的前面一个,我们需要返回 slow 的下一个节点。
代码:
public ListNode middleNode(ListNode head) {if (head == null || head.next == null) {return head;}ListNode fast = head;ListNode slow = head;while (fast != null && fast.next != null) {fast = fast.next.next;slow = slow.next;}return slow;
}
快慢指针优缺点:
快慢指针是一种常用的优化技巧,它有以下的优点:
- 它可以在不使用额外空间的情况下,解决一些链表或数组的问题,如判断是否有环,找到中间节点,找到倒数第k个节点等。
- 它可以在一次遍历中,得到一些有用的信息,如环的长度,环的入口,链表的长度等。
- 它可以简化代码的逻辑,避免使用多重循环或递归。
快慢指针也有一些缺点,如:
- 它需要对链表或数组的结构有一定的了解,才能正确地设置快慢指针的步长和终止条件。
- 它可能会遇到一些边界情况,如链表为空,链表只有一个节点,链表长度为偶数或奇数等,需要特别注意处理。
- 它可能会造成一些误解或困惑,如快慢指针相遇时,它们是否在环的入口,是否在环的中点,是否在链表的中点等。需要仔细分析和证明。
对撞指针
对撞指针介绍:
对撞指针是一种设置在序列两端向中间移动的两个指针,用于解决数组中的问题,如找到两数之和,反转元音字母等。对撞指针的核心思想是利用数组的有序性,根据两个指针所指元素的和与目标值的大小关系,决定移动哪个指针,从而减少不必要的遍历,优化时间复杂度。下面我们将通过一些例题来展示对撞指针的用法和技巧。
对撞指针例题
例题1:找到两数之和
给定一个已按照 升序排列 的有序数组 nums ,和一个目标值 target 。请你在该数组中找出 和为目标值 的那 两个 整数,并返回它们的数组下标。
假设每种输入只会对应一个答案,但是,数组中同一个元素不能使用两遍。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums1 == 9 ,返回 [0, 1] 。 示例 2:
输入:nums = [2,3,4], target = 6 输出:[0,2] 示例 3:
输入:nums = [-1,0], target = -1 输出:[0,1]
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/two-sum-ii-input-array-is-sorted
思路:我们可以使用对撞指针来解决这个问题。首先,我们定义两个指针 left 和 right ,并让它们分别指向数组的首尾元素。然后,我们计算 left 和 right 所指元素的和 sum ,并与目标值 target 比较。如果 sum 等于 target ,那么我们就找到了答案,返回 left 和 right 的下标。如果 sum 小于 target ,那么我们就让 left 向右移动一位,增大 sum 的值。如果 sum 大于 target ,那么我们就让 right 向左移动一位,减小 sum 的值。我们重复这个过程,直到找到答案或者 left 和 right 相遇。
代码:
public int[] twoSum(int[] numbers, int target) {if (numbers == null || numbers.length < 2) {return new int[0];}int left = 0;int right = numbers.length - 1;while (left < right) {int sum = numbers[left] + numbers[right];if (sum == target) {return new int[]{left + 1, right + 1};} else if (sum < target) {left++;} else {right--;}}return new int[0];
}
例题2:反转元音字母
编写一个函数,以字符串作为输入,反转该字符串中的元音字母。
示例 1:
输入:“hello” 输出:“holle” 示例 2:
输入:“leetcode” 输出:“leotcede”
思路:我们可以使用对撞指针来解决这个问题。首先,我们定义两个指针 left 和 right ,并让它们分别指向字符串的首尾字符。然后,我们判断 left 和 right 所指字符是否都是元音字母(a,e,i,o,u)。
如果是,那么我们就交换 left 和 right 所指字符的位置,然后让 left 向右移动一位,right 向左移动一位。如果不是,那么我们就让不是元音字母的指针向中间移动,直到找到元音字母或者 left 和 right 相遇。
代码:
public String reverseVowels(String s) {if (s == null || s.length() < 2) {return s;}char[] chars = s.toCharArray();int left = 0;int right = chars.length - 1;String vowels = "aeiouAEIOU";while (left < right) {if (!vowels.contains(chars[left] + "")) {left++;} else if (!vowels.contains(chars[right] + "")) {right--;} else {char temp = chars[left];chars[left] = chars[right];chars[right] = temp;left++;right--;}}return new String(chars);
}
对撞指针优缺点:
对撞指针有以下的优点:
- 它可以在不使用额外空间的情况下,解决一些有序数组的问题,如找到两数之和,反转元音字母等。
- 它可以在一次遍历中,得到一些有用的信息,如数组中是否存在满足条件的元素对,反转后的字符串等。
- 它可以简化代码的逻辑,避免使用多重循环或二分查找。
对撞指针也有一些缺点,如:
- 它需要对数组的有序性有一定的了解,才能正确地设置对撞指针的移动方向和终止条件。
- 它可能会遇到一些边界情况,如数组为空,数组只有一个元素,数组中没有满足条件的元素对等,需要特别注意处理。
- 它可能会造成一些误解或困惑,如对撞指针相遇时,它们是否在数组的中点,是否在满足条件的元素对的最小或最大位置等。需要仔细分析和证明。
更新中——未完
总结
🐋 🐬 🐶 🐳 🐰 🦀☝️ ⭐ 👉 👀
如果你对这篇文章感兴趣,欢迎在评论区留言,分享你的想法和建议。如果你喜欢我的博客,请记得点赞、收藏和关注我,我会持续更新更多有用的网页技巧和教程。谢谢大家!
更多宝藏
🍇🍉🍊🍏🍋🍅🥝🥥🫒🫕🥗
项目仓库看这里🤗:
https://github.com/w-x-x-w
https://gitee.com/w-_-x
博客文章看这里🤭:
https://blog.csdn.net/weixin_62650212
视频推送看这里🤤:
https://space.bilibili.com/1909782963
相关文章:

算法详解-双指针算法的魅力-一种简单而高效的编程思想
文章目录双指针简介快慢指针快慢指针介绍快慢指针例题快慢指针优缺点:对撞指针对撞指针介绍:对撞指针例题对撞指针优缺点:更新中——未完总结更多宝藏双指针简介 😎🥳😎🤠😮&#x…...

网页审查元素
在讲解爬虫内容之前,我们需要先学习一项写爬虫的必备技能:审查元素(如果已掌握,可跳过此部分内容)。1、审查元素在浏览器的地址栏输入URL地址,在网页处右键单击,找到检查。(不同浏览器的叫法不同…...

gpt2 adapter finetune
1. 安装依赖: pip install -U adapter-transformers pip install datasets 2.训练代码: from datasets import load_dataset from transformers import AutoModelForCausalLM from transformers import GPT2Tokenizer from transformers import Adap…...

Day14_文件操作
一、数据存储 1.1 计算机数据存储 计算机内存分为运行内存和硬盘两种:保存在运行内存中的数据在程序运行结束后会自动释放,保存在硬盘中的数据会一直存在(除非手动删除或者硬盘损坏) 1)打开文件 open(文件路径, 文件打开方式‘r’, encod…...

leetcode 轮转数组 189
题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,7,1,2…...

Leetcode.1849 将字符串拆分为递减的连续值
题目链接 Leetcode.1849 将字符串拆分为递减的连续值 Rating : 1747 题目描述 给你一个仅由数字组成的字符串 s。 请你判断能否将 s拆分成 两个或者多个 非空子字符串 ,使子字符串的 数值 按 降序 排列,且每两个 相邻子字符串 的数值之 差 …...

Android布局层级过深为什么会对性能有影响?为什么Compose没有布局嵌套问题?
做过布局性能优化的同学都知道,为了优化界面加载速度,要尽可能的减少布局的层级。这主要是因为布局层级的增加,可能会导致测量时间呈指数级增长。 而Compose却没有这个问题,它从根本上解决了布局层级对布局性能的影响: Compose界…...
【UR机械臂CB3 网络课程 】
【UR机械臂CB3 网络课程 】1. 前言2. 概览:特色与术语2.1 机器人组成2.1.1控制柜2.1.2 UR 机器人手臂2.2 接通机器人电源2.3 移动机械臂3. 机器人如何工作3.1 选择臂端工具3.2 输入有关臂端工具的信息3.3 连接外部装置3.4 机器人编程4. 设置工具4.1 末端执行器配置4.2 工具中心…...

dp-统计字典序元音字符串的数目
给你一个整数 n,请返回长度为 n 、仅由元音 (a, e, i, o, u) 组成且按 字典序排列 的字符串数量。 字符串 s 按 字典序排列 需要满足:对于所有有效的 i,s[i] 在字母表中的位置总是与 s[i1] 相同或在 s[i1] 之前。 示例 1: 输入&…...
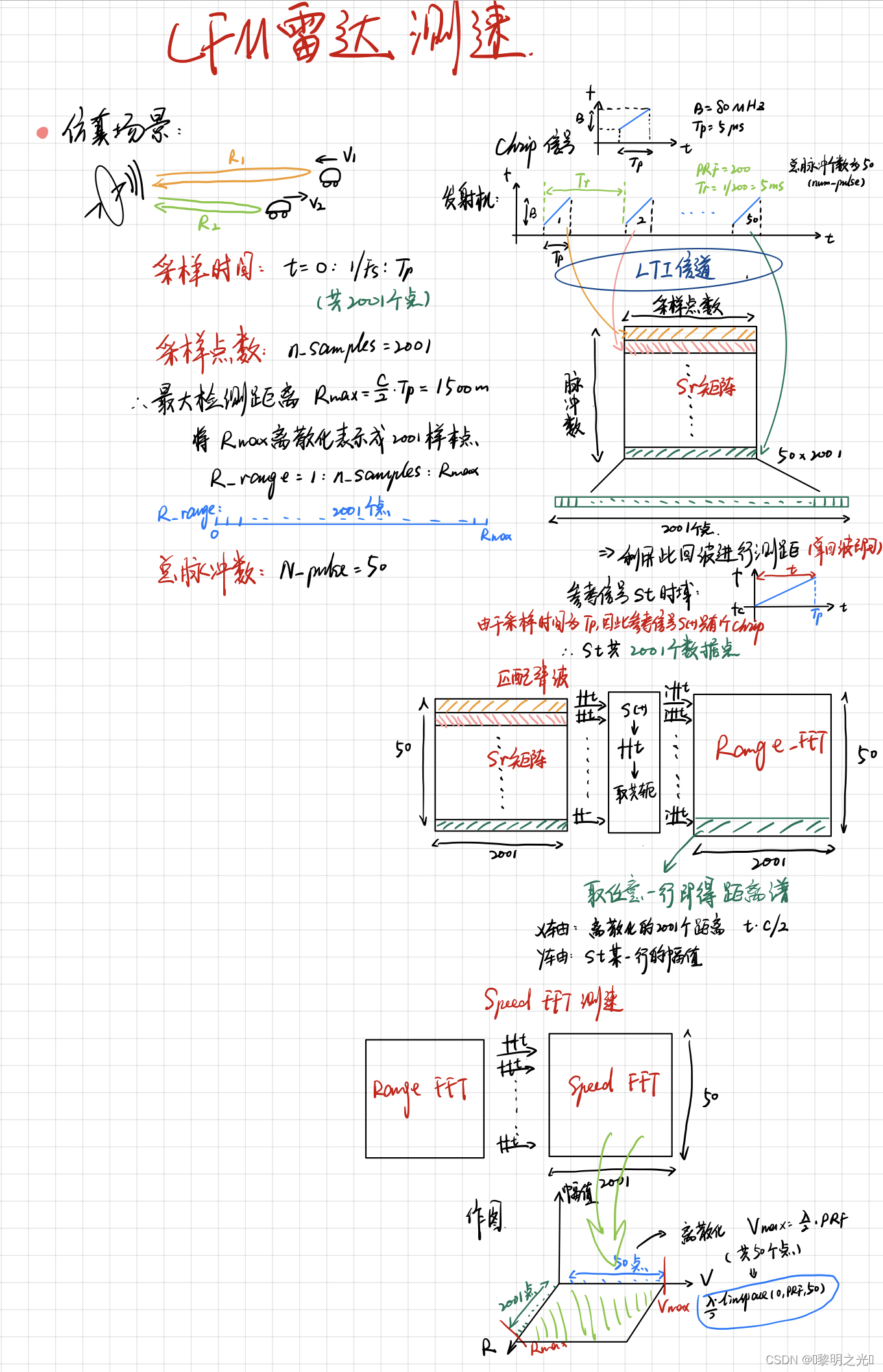
LFM雷达实现及USRP验证【章节3:连续雷达测距测速】
第一章介绍了在相对速度为0时候的雷达测距原理 目录 1. LFM测速 1.1 雷达测速原理 1.2 Chrip信号测速 2. LFM测速代码实现 参数设置 仿真图像 matlab源码 代码分析 第一章介绍了在相对速度为0时候的雷达测距原理,第二章介绍了基于LFM的雷达测距原理及其实现…...

COLMAP多视角视图数据可视化
这篇博文主要介绍多视角三维重建的实用工具COLMAP。为了让读者更快确定此文是否为自己想找的内容,我先用简单几句话来描述此文做的事情: 假设我们针对一个物体(人)采集了多个(假设60个)视角的照片ÿ…...

2023年全国最新高校辅导员精选真题及答案36
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 92.校园文化形成与发展的主要影响因素有() A.学校的领导与管理活…...

ThreeJS-全屏和退出全屏、自适应大小(五)
下载新得组件 npm install gsap -S 新引入 import gsap from gsap //动画控制 代码: <template> <div id"three_div"> </div> </template> <script> import * as THREE from "three"; import {OrbitControls } f…...

等级保护2.0要求及所需设备清单
等级保护的工作流程包括定级、备案、建设整改、等级测评,核心思想在于建立“可信、可控、可管”的安全防护体系,使得系统能够按照预期运行,免受信息安全攻击和破坏。 三级等保要求及所需设备 三级等级保护指标项: 物理访问控制…...

【大数据之Hadoop】六、HDFS之NameNode、Secondary NameNode和DataNode的内部工作原理
NN和2NN的内部工作原理 对于NameNode的存放位置: 内存中:好处:计算快 坏处:可靠性差,断电后元数据会丢失 磁盘中:好处:可靠性搞 坏处:计算慢 内存磁盘中:效率低 所以设…...

小黑子—Java从入门到入土过程:第四章
Java零基础入门4.0Java系列第四章1. 顺序结构2. if语句3. switch 语句3.1 default的位置和省略3.2 case 穿透3.3 switch 新特性 (jdk12开始)4. for 循环5. while 循环6.do...while 循环7. 无限循环8. 跳转控制语句9. 练习9.1 逢七过9.2 平方根9.3 求质数…...
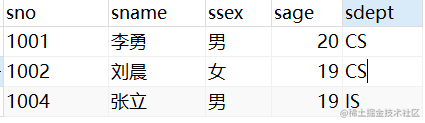
数据库原理及应用(四)——SQL语句(2)SQL基础查询以及常见运算符
一、SELECT语句基础 数据库查询是数据库的核心操作,SELECT 语句用于从数据库中选取数据。 SELECT [ALL/DISTINCT] <列名>,<列名>...FROM <表名或视图名>,<表名或视图名>[WHERE <条件表达式>][GROUP BY <列名1> [HAVING <条…...

(算法基础)Floyd算法
适用情景Floyd算法适用于多源汇最短路,也就是他问你比如说从3号点到6号点的最短路距离,比如说从7号点到20号点的最短路距离,而不是单源最短路(从1号点到n号点的最短路距离)。在这个算法当中允许负权边的存在。但在求最…...

SQL语法:浅析select之七大子句
Mysql版本:8.0.26 可视化客户端:sql yog 目录一、七大子句顺序二、演示2.1 from语句2.2 on子句2.3 where子句2.4 group by子句2.4.1 WITHROLLUP,加在group by后面2.4.2 是否可以按照多个字段分组统计?2.4.3 分组统计时,…...

中国人民大学与加拿大女王大学金融硕士——去有光的地方,并成为自己的光
光是我们日常生活中一个重要的元素,试想一下如果没有光,世界将陷入一片昏暗。人生路亦是如此,我们从追逐光、靠近光、直到自己成为光。人民大学与加拿大女王大学金融硕士项目是你人生路上的一束光吗 渴望想要成为一个更好的人,就…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
