【算法】BFS—解开密码锁的最少次数
题目
一个密码锁由 4 个环形拨轮组成,每个拨轮都有 10 个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,请给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
解题
第一步,我们不管所有的限制条件,不管 deadends 和 target 的限制,就思考一个问题:如果让你设计一个算法,穷举所有可能的密码组合,你将怎么做?
总共有4个位置,每个位置可以向上转,也可以向下转,也就是有8种可能。比如,从 '0000' 开始,转一次,可以穷举出 '1000' ,'9000','0100','0900'······共8种密码。然后,再以这8种密码作为基础,对每种密码再转一下,穷举出所有可能······
仔细想想,这就可以抽象成一幅图,每个节点有8个相邻的节点,求的又是最短距离,这不就是典型的BFS嘛,这时框架就可以派上用场了,先写出一个“简陋”的BFS框架代码:
package BFS;import java.util.LinkedList;
import java.util.Queue;// leetcode 109 打开转盘锁
public class OpenTheTurntable {public String plusOne(String str, int j) {char[] ch = str.toCharArray();if (ch[j] == '9') {ch[j] = '0';} else {ch[j] += 1;}return new String(ch);}public String minusOne(String str, int j) {char[] ch = str.toCharArray();if (ch[j] == '0') {ch[j] = '9';} else {ch[j] -= 1;}return new String(ch);}// BFS框架伪码,打印所有可能的密码public void BFS(String target) {Queue<String> queue = new LinkedList<>();queue.offer("0000");while (!queue.isEmpty()) {int sz = queue.size();// 将当前队列中的所有节点向周围扩散for (int i = 0; i < sz; i++) {String cur = queue.poll();// 判断是否到达终点System.out.println(cur);// 将一个节点的相邻节点加入队列for (int j = 0; j < 4; j++) {String up = plusOne(cur, j);String down = minusOne(cur, j);queue.offer(up);queue.offer(down);}}// 在这里增加步数}return;}}注意:这段代码当然有很多问题,但是我们做算法题肯定不是一蹴而就的,而是从简陋到完美的。
这段BFS代码已经能够穷举所有可能的密码组合了,但是显然不能完成题目,还有如下问题需要解决:
1.会走回头路。比如,从 '0000' 拨到 '1000',但是等从队列中拿出 '1000'时,还会拨出一个 '0000',这样会产生死循环。
2.没有终止条件,按照题目要求,找到 target 就应该结束并返回拨动的次数。
3.没有对 deadends的处理,按道理这些“死亡密码”是不能出现的,也就是说遇到这些密码的时候需要跳过,不能进行任何操作。
只要按照BFS框架在对应的位置稍微修改即可修复这些问题:
package BFS;import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Set;// leetcode 109 打开转盘锁
public class OpenTheTurntable {public String plusOne(String str, int j) {char[] ch = str.toCharArray();if (ch[j] == '9') {ch[j] = '0';} else {ch[j] += 1;}return new String(ch);}public String minusOne(String str, int j) {char[] ch = str.toCharArray();if (ch[j] == '0') {ch[j] = '9';} else {ch[j] -= 1;}return new String(ch);}int openLock(String[] deadends, String target) {// 记录需要跳过的死亡密码Set<String> deads = new HashSet<>();for (String s : deadends) {deads.add(s);}// 记录已经穷举过的密码,防止走回头路Set<String> visited = new HashSet<>();Queue<String> queue = new LinkedList<>();// 从起点开始启动广度优先搜索int step = 0;queue.offer("0000");visited.add("0000");while (!queue.isEmpty()) {int sz = queue.size();// 将当前队列中的所有节点向周围扩散for (int i = 0; i < sz; i++) {String cur = queue.poll();// 判断密码是否合法,是否到达终点if (deads.contains(cur)) {continue;}if (cur.equals(target)) {return step;}// 将一个节点的相邻节点加入队列for (int j = 0; j < 4; j++) {String up = plusOne(cur, j);if (!visited.contains(up)) {queue.offer(up);visited.add(up);}String down = minusOne(cur, j);if (!visited.contains(down)) {queue.offer(down);visited.add(down);}}}// 在这里增加步数step += 1;}// 如果穷举完都没有找到目标密码,那就是找不到了return -1;}public static void main(String[] args) {OpenTheTurntable openTheTurntable = new OpenTheTurntable();String[] deadends = {"8888"};int count = openTheTurntable.openLock(deadends, "0008");System.out.println(count);}}
至此,这道题目就解决了。但优化还没有结束,因为终点在哪里是知道的,所以可以用双向BFS进行优化。这里先留白,以后再补充······
相关文章:

【算法】BFS—解开密码锁的最少次数
题目 一个密码锁由 4 个环形拨轮组成,每个拨轮都有 10 个数字: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 。每个拨轮可以自由旋转:例如把 9 变为 0,0 变为 9 。每次旋转都只能旋转一个拨轮的一位数字。 锁的初始数字为 0000 ,一个…...

非守护线程会阻止JVM的终止吗
非守护线程会阻止JVM的终止。在Java中,线程分为守护线程(Daemon Threads)和非守护线程(Non-Daemon Threads,也被称为用户线程)。这两种线程在JVM终止时表现出不同的行为。 非守护线程是JVM中执行程序主要逻…...

Grafana面板-linux主机详情(使用标签过滤主机监控)
1. 采集器添加labels标签区分业务项目 targets添加labels (模板中使用的project标签) … targets: [‘xxxx:9100’] labels: project: app2targets: [‘xxxx:9100’] labels: project: app1 … 2. grafana面板套用 21902 模板 演示...

MYSQL数据库基础篇——DDL
DDL:DDL是数据定义语言,用来定义数据库对象。 一.DDL操作数据库 1.查询 ①查询所有数据库 输入; 得到结果: ②查询当前数据库 输入; 例如执行下面语句: 2.创建 输入 然后展示数据库即可得到结果&…...

Springboot 集成 Swing
背景 Springboot 在 Java 给 Java 开发带来了极大的便利,那么如何把它集成到 Swing GUI 编程项目中,使得 GUI 编程更加高效?本人简单做了一下尝试,完成一个 demo ,贴出来供大家参考 具体步骤 创建一个 spring boot …...

枚举算法总结
枚举算法(Enumeration Algorithm)是一种简单而直接的算法设计策略,它通过列出问题的所有可能情况,逐一进行验证,直到找到问题的解。这种算法适用于问题的解空间不是太大,可以通过遍历所有情况来找到答案的情…...

编译 Android 11源码
参考小米6 lineageos官方编译文档:https://wiki.lineageos.org/devices/sagit/build 单独编译 framework 以LineageOS18.1(Android 11)为例: 1、在源码根目录执行: make framework-minus-apex 2、用生成的framewo…...

时间复杂度计算 递归(solve2 后续)
原帖 最近校内比较忙,更新缓慢,致歉。 这里函数每次都需要遍历 h h h 和 m m m 之间的数(复杂度 O ( n ) O(n) O(n)),所以和 solve1 略有不同。仍然假设 T ( n ) \operatorname{T}(n) T(n) 表示 m − h 1 n…...

Nginx:高性能Web服务器与反向代理的深度剖析
Nginx:高性能Web服务器与反向代理的深度剖析 Nginx(发音为“engine X”)是一款轻量级但功能强大的Web服务器和反向代理服务器,以其高并发处理能力、低内存占用和灵活的扩展性在互联网项目中得到了广泛应用。本文将深入探讨Nginx…...

JavaSE - 面向对象编程03
01 多态 01_01 认识多态 01_02 多态的好处和缺点 【1】好处:① 可以解耦合,扩展性更强,父类引用指向的子类对象可以随时切换,而后面的逻辑代码并不需要更改。 ② 使用父类引用可以作为方法的形参或返回类型来接收一切子类对象。…...

变电站缺陷数据集8307张,带xml标注和txt标注,可以直接用于yolo训练
变电站缺陷数据集8307张, 带xml标注和txt标注,可以直接用于yolo训练,赠附五个脚本 变电站缺陷数据集 数据集概述 变电站缺陷数据集是一个专门针对变电站设备和环境缺陷检测的图像数据集。该数据集包含了8307张经过标注的图像,旨…...

Redis的存储原理和数据模型
一、Redis是单线程还是多线程呢? 我们通过跑redis的代码,查看运行的程序可以得知,Redis本身其实是个多线程,其中包括redis-server,bio_close_file,bio_aof_fsync,bio_lazy_free,io_t…...

Linux 文件与目录操作命令详解
文章目录 前言创建文件1. touch2. vim 文件内容显示3. cat4. more5. less6. head7. tail 文件(目录)复制、删除和移动8. cp9. rm10. mv 压缩文件与解压缩11. gzip12. zip 和 unzip 创建目录13. mkdir 删除目录14. rmdir 改变工作目录15. cd16. pwd 显示目…...
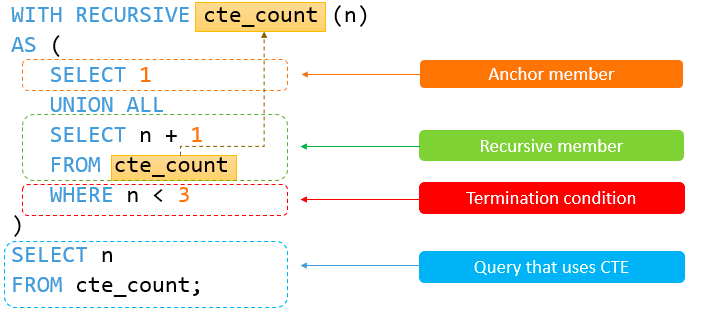
MySQL篇(窗口函数/公用表达式(CTE))
目录 讲解一:窗口函数 一、简介 二、常见操作 1. sumgroup by常规的聚合函数操作 2. sum窗口函数的聚合操作 三、基本语法 1. Function(arg1,..., argn) 1.1. 聚合函数 sum函数:求和 min函数 :最小值 1.2. 排序函数 1.3. 跨行函数…...

408算法题leetcode--第七天
283. 移动零 283. 移动零思路:代码中注释阐述时间:O(n);空间:O(1) class Solution { public:void moveZeroes(vector<int>& nums) {// 简单思路:用一个辅助数组,将非0元素复制到里面// 双指针&…...

政务安全体系构建中的挑战
在数字化政务安全体系的构建过程中,面临着几个关键的挑战: ▋挑战一:安全防护滞后现代网络攻击技术不断演进,攻击手段日益多样化,如高级持续性威胁(APT)和勒索软件等新型攻击方式频繁出现。这些…...

基于EchoMimic加速版,可编辑标志点控制实现逼真音频驱动的肖像动画
EchoMimic 是蚂蚁集团终端技术部门开发的一项技术,旨在通过音频驱动生成逼真的肖像动画。对于那些初次接触这项技术的用户,本教程将带你逐步了解如何设置开发环境、获取项目代码、安装依赖,并最终成功运行示例生成自己的肖像动画。 文章目录 项目代码安装依赖业务拓展参数调…...

【STM32 HAL库】IIC通信与CubeMX配置
【STM32 HAL库】IIC通信与CubeMX配置 前言理论IIC总线时序图IIC写数据IIC读数据 轮询模式CubeMX配置应用示例AHT20初始化初始化函数读取说明读取函数 中断模式CubeMX配置状态机图fsm.caht20.c DMA模式CubeMX配置代码 前言 本文为笔者学习 IIC 通信的总结,基于keysk…...

iPhone 上丢失了重要的联系人?如何恢复已删除的 iPhone 联系人
丢失 iPhone 上的联系人可能会带来灾难。无论是一份很棒的新工作机会、潜在的恋爱对象,还是您一直想打电话的老朋友,如果您打开“联系人”应用时看到空白,这绝不是好事。不过,一切并非全无,仍然可以通过备份或专业软件…...

【有啥问啥】弱监督学习新突破:格灵深瞳多标签聚类辨别(Multi-Label Clustering and Discrimination, MLCD)方法
弱监督学习新突破:格灵深瞳多标签聚类辨别(Multi-Label Clustering and Discrimination, MLCD)方法 引言 在视觉大模型领域,如何有效利用海量无标签图像数据是一个亟待解决的问题。传统的深度学习模型依赖大量人工标注数据&…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
