数据结构------二叉树简单介绍及实现
如果不是满二叉树或者完全二叉树,就要用链式存储
//搜索二叉树:左子树的所有值比根小,右子树的所有值比根大
// 实现查找,最多找高度次(类似二分法)
//二分查找存在的问题:排序;必须对数组操作,插入删除不方便。
//同一个函数不同的值递归占用的空间是一样的,因为销毁了之后再接着用
//不能递归的深度太深,不然会导致栈溢出
//这段二叉树的递归代码编译完了之后是一份指令,这份指令会自己调用自己,不断建立栈帧,然后销毁栈帧
//一些基本知识点
满二叉树每层节点个数构成一个等比数列
增加一个度为1的节点,一定减少一个度为0的节点。增加一个度为2的节点,一定增加一个度为0的,减少一个度为1的。因为0变到1再变到2。
//由性质3得:
//注意:完全二叉树度为1的节点只可能为1或0
//用满二叉树公式来推,计算一个大概的范围
//根据前序.中序序列写出二叉树
//前序确定根,中序分割左右子树
//一定注意7是右子树,因为中序是左根右
//递归的逻辑过程
//递归的物理过程
//通过ebp(高地址,用来保存主调函数的下一行指令)和esp(低地址,不断建立栈帧开辟空间)
//static静态变量只初始化一次,在多次调用的时候会出现问题,可以改为指针或全局变量(最好不要用),全局变量每次使用的时候记得进行初始化
//求节点个数采用分治思想:分而治之,上一层来指挥下一层
//求叶子节点个数:
//这样写就出错了,当该树为空或者没有左/右结点的时候,访问空指针的下一个节点就崩溃了
//所以应该单独讨论节点为空的时候
//求二叉树高度:
//错误做法:效率问题,超出时间限制
计算左/右子树高度值,左边递归到6,6的左右节点都为0,然后6的值为1。
然后回溯到3,3的左子树返回0,右子树返回1,相比较右子树高度大,即计算右子树高度+1,又因为此时并没有保存6的高度为1这个值,还要继续计算3的右子树6的左子树和右子树的高度值再比较然后再回溯到3,把值+1赋值给3这个节点。
然后3向上回溯到2,2的左子树的高度值为2,右子树高度值为0,相比较应该取左子树的高度值。但此时这个值并没有保存下来,应该再计算3的高度值,此时3的高度值未知,要比较3的左右子树的高度值......(计算方法同上一段)
//综述:节点深度越深,该节点计算次数成倍数增加
//正确做法(把值记录下来):
//总的代码:
//实现二叉树
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node5->right = node7;return node1;
}//遍历只需要注意顺序就好,打印的都是data
//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}int fun(int n)
{if (n == 0)return 0;return fun(n - 1) + n;
}// 错误示范
//错因:不能用静态变量,因为如果调用多次这个函数的话,size是一直累加的
// 不能计算出每一次调用时的节点个数
//int TreeSize(BTNode* root)
//{
// static int size = 0;
// if (root == NULL)
// return 0;
// else
// ++size;
//
// TreeSize(root->left);
// TreeSize(root->right);
//
// return size;
//}
//以下两种解法太复杂
//解法1:把它变成全局变量,并且要注意在每次主函数中调用该函数之前要把size初始化为零
//int size = 0;
//int TreeSize(BTNode* root)
//{
// if (root == NULL)
// return 0;
// else
// ++size;
//
// TreeSize(root->left);
// TreeSize(root->right);
//
// return size;
//}
//解法2:把size的指针传进去,通过指针解引用再++来改变size的值
//void TreeSize(BTNode* root, int* psize)
//{
// if (root == NULL)
// return 0;
// else
// ++(*psize);
//
// TreeSize(root->left, psize);
// TreeSize(root->right, psize);
//}//求节点个数
//采用分治递归的思想
//1.该节点不存在:节点数为零
//2.该节点存在,节点数=左子树节点数+右子树节点数+1
int TreeSize(BTNode* root)
{return root == NULL ? 0 :TreeSize(root->left) + TreeSize(root->right) + 1;
}//求叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left)+ TreeLeafSize(root->right);
}//求深度(树高)
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}// 有效率问题
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return TreeHeight(root->left) > TreeHeight(root->right) ?TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}//int fmax(int x, int y)
//{
// return x > y ? x : y;
//}//int TreeHeight(BTNode* root)
//{
// if (root == NULL)
// return 0;
//
// return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
//}int main()
{BTNode* root = CreatBinaryTree();PrevOrder(root);printf("\n");InOrder(root);printf("\n");//递归太深导致栈溢出//printf("%d\n", fun(10000));/*int size = 0;TreeSize(root, &size);printf("TreeSize:%d\n",size);size = 0;TreeSize(root, &size);printf("TreeSize:%d\n", size);*/printf("TreeSize:%d\n", TreeSize(root));printf("TreeLeafSize:%d\n", TreeLeafSize(root));printf("TreeHeight:%d\n", TreeHeight(root));return 0;
}相关文章:

数据结构------二叉树简单介绍及实现
如果不是满二叉树或者完全二叉树,就要用链式存储 //搜索二叉树:左子树的所有值比根小,右子树的所有值比根大 // 实现查找,最多找高度次(类似二分法) //二分查找存在的问题:…...

由一个 SwiftData “诡异”运行时崩溃而引发的钩深索隐(六)
概述 在 WWDC 24 中,苹果推出了数据库框架 SwiftData 2.0 版本。听说里面新增了能让数据记录“借尸还魂”的绝妙法器,到底是真是假呢? 我们在上篇博文中介绍了 History Trace 是如何稳妥的处理数据删除操作的。而在这里,我们将继续介绍 SwiftData 2.0 中另一个新特性:“墓…...

尚品汇-秒杀下单实现-页面轮询查询订单状态(五十三)
目录: (1)整合秒杀业务 (2)秒杀下单 (3)秒杀下单监听 (4)页面轮询接口 (1)整合秒杀业务 秒杀的主要目的就是获取一个下单资格,拥…...

2024年微电子与纳米技术国际研讨会(ICMN 2024) Microelectronics and Nanotechnology
文章目录 一、会议详情二、重要信息三、大会介绍四、出席嘉宾五、征稿主题六、咨询 一、会议详情 二、重要信息 大会官网:https://ais.cn/u/vEbMBz提交检索:EI Compendex、IEEE Xplore、Scopus大会时间:2024年9月20-22日地点:成都…...

2024最新版,人大赵鑫老师《大语言模型》新书pdf分享
本书主要面向希望系统学习大语言模型技术的读者,将重点突出核心概念与 算法,并且配以示例与代码(伪代码)帮助读者理解特定算法的实现逻辑。由于大语言模型技术的快速更迭,本书无法覆盖所有相关内容,旨在梳理…...

[Leetcode 543][Easy]-二叉树的直径-递归
目录 一、题目描述 二、整体思路 三、代码 一、题目描述 原题地址 二、整体思路 取一个结点的最大直径就是取一个结点的左子树最大深度右子树最大深度之和,因此可以定义一个递归函数,作用是取一个结点的最大直径。这个函数中还实现了求左子树最大深度…...

高级大数据开发学习路线指南
掌握大数据技术是一项系统性工程,涉及到广泛的技能和专业知识。为了帮助初学者构建坚实的基础,并逐步成长为大数据领域的专家,下面详细阐述了一条全面而深入的学习路线: 1. Java 编程基础 - 打造坚实的底层技能 关键知识点&…...

SpringBoot设置mysql的ssl连接
因工作需要,mysql连接需要开启ssl认证,本文主要讲述客户端如何配置ssl连接。 开发环境信息: SpringBoot: 2.0.5.RELEASE mysql-connector-java: 8.0.18 mysql version:8.0.18 一、检查服务端是否开启ssl认…...
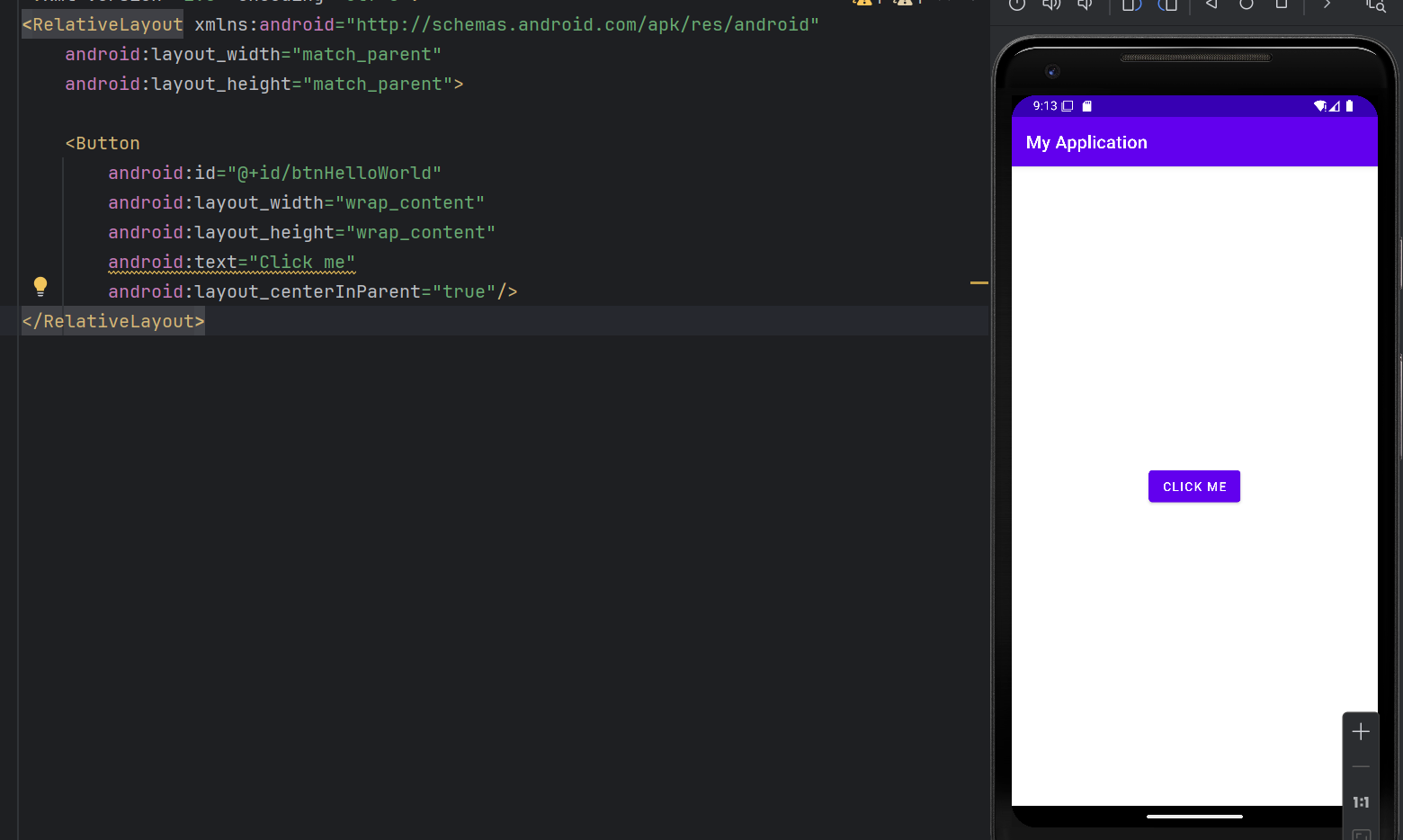
2024-1.2.12-Android-Studio配置
本地博客: https://k1t0111.github.io/ K1T0 最近在做一些app方向的移动技术开发学习,但是由于AS的配置问题,市面上找不到最新的2024版本的AS的相关配置。笔者也是踩了很多坑,因此想写一篇文章记录一下最新的AS 2024 1.2.12的对应java环境的一…...
:vue2+vite封装v-resize指令,实现左侧树拖拽宽度和折叠展开)
前端vue左侧树的一整套功能实现(一):vue2+vite封装v-resize指令,实现左侧树拖拽宽度和折叠展开
实现v-resize指令,具体以下功能: 指令接收宽度最大最小值,接收一个id用于localStorage存储拖拽宽度,接收padding拖拽时产生虚线拖拽,松开鼠标再进行元素宽度调整折叠展开图标使用本地图片 封装一个vite下使用本地图片…...

本地部署huggingface模型,建立自己的翻译应用
过去,我们使用翻译接口时,往往都是使用百度等的接口,每天有一定量的免费额度。今天为大家介绍一个可以进行翻译的模型,具备英译中、中译英的能力。并且在这个过程中,向大家介绍一个如何在本地部署模型。在之前的”五天…...

基于python+django+vue的在线学习资源推送系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、SSM项目源码 系统展示 【2025最新】基于协同过滤pythondjangovue…...

.Net Gacutil工具(全局程序集缓存工具)使用教程
GAC介绍: GAC(Global Assembly Cache)全局程序集缓存,是用于存放.Net应用程序共享的程序集。 像平常我们在Visual Studio中引用系统程序集时,这些程序集便来自于GAC。 GAC默认位置为:%windir%\Microsoft…...

安卓13修改设置设备型号和设备名称分析与更改-android13设置设备型号和设备名称更改
总纲 android13 rom 开发总纲说明 文章目录 1.前言2.问题分析3.代码分析4.代码修改5.编译6.彩蛋1.前言 用户要定制一些系统显示的设备型号和设备名称,这就需要我们分析设置里面的相关信息来找到对应的位置进行修改了。 2.问题分析 像这种信息要么是config.xml里面写死了,要…...

AI健身体能测试之基于paddlehub实现引体向上计数个数统计
【引体向上计数】 本项目使用PaddleHub中的骨骼检测模型human_pose_estimation_resnet50_mpii,进行人体运动分析,实现对引体向上的自动计数。 1. 项目介绍 人体运动分析是近几年许多领域研究的热点问题。在学科的交叉研究上,人体运动分析涉…...

Redis常见报错及解决方法总结
Redis常见报错及解决方法总结 Redis作为高效的内存数据库,在实际使用过程中不可避免会遇到一些问题和报错。为了帮助大家更好地应对这些问题,我将常见的Redis报错及其解决方法进行总结,并提供具体的操作步骤。 1. Connection Refused 错误…...

【TabBar嵌套Navigation案例-JSON的简单使用 Objective-C语言】
一、JSON的简单使用 1.我们先来看一下示例程序里边,产品推荐页面, 在我们这个产品推荐页面里面, 它是一个CollectionViewController,注册的是一个xib的一个类型,xib显示这个cell,叫做item,然后,这个邮箱大师啊,包括这个图标,以及这些东西,都是从哪儿来的呢,都是从…...
)
通过鼠标移动来调整两个盒子的宽度(响应式)
DOM结构: <div class"courer"> // 外层盒子<div class"dividing-line" title"拖动"></div> // 拖动的那个线<div class"course-title-box"> // 第一个盒子<div class"course-content-…...

React Zustand状态管理库的使用
Zustand 是一个轻量级的状态管理库,适用于 React 和浏览器环境中的状态管理需求。它由 Vercel 开发并维护,旨在提供一种简单的方式来管理和共享状态。Zustand 的设计理念是尽可能简化状态管理,使其更加直观和易于使用。 Zustand 官网点击跳转…...

pyrosetta MoveMap介绍
在 PyRosetta 中,MoveMap 是一个非常重要的类,用来控制蛋白质分子中哪些部分可以在某些操作(如折叠、旋转、优化等)中被移动。MoveMap 允许你精确地指定哪些残基、键角或原子可以进行特定的运动,从而帮助你在蛋白质结构预测、优化和设计中进行灵活的控制。 MoveMap 的功能…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...




















